Hans Walser, [20180518]

Würfelstapel

1 Worum geht es?

Würfel sollen so gestapelt werden, dass ihre Mittelpunkte ein flächenzentriertes kubisches Punktgitter ergeben.

2 Quadratische Basis

2.1 Berechnung

Die Abbildung 1 zeigt das Minimalmodell mit quadratischer Basis.

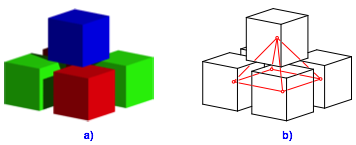
Abb. 1: Quadratische Basis

Die Bedingung für ein flächenzentriertes kubisches Punktgitter verlangt, dass die Abstände zwischen den Würfelmittelpunkten (rot in Abb. 1b) alle gleich lang sind.

Wir arbeiten mit Würfeln der Kantenlänge 1 und bezeichnen den roten Abstand mit x. Die durch die roten Abstände gebildete Pyramide hat die Höhe 1. Damit erhalten wir die Bedingung:

(1)

Dies führt zur positiven Lösung:

(2)

2.2 Beispiele und Ansichten

Die Abbildung 2 zeigt ein Holzmodell.

Abb. 2: Holzmodell

Die Abbildung 3 zeigt eine größere Basis und die Pyramide.

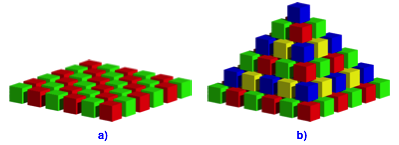
Abb. 3: Pyramide

Die Abbildung 4 zeigt die Situation von vorne und von oben.

Abb. 4: Von vorne und von oben

2.3 Verdrehung der Würfel

Die Würfel einer Lage haben einen Zwischenraum von . Wir können sie daher um die senkrechte Achse um 45° verdrehen. Dann berühren sich die Würfel einer Lage an den senkrechten Kanten (Abb. 5).

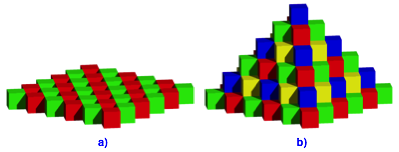
Abb. 5: Würfelchen um 45° verdreht

Allerdings haben wir nun zwischen den Würfelchen einer Lage würfelförmige Löcher. Die Pyramide der Abbildung 5b würde ohne zusätzliche Stützwürfel in den Löchern in sich um die halbe Höhe zusammensacken.

Die Abbildung 6 zeigt die neue Situation von vorne und von oben.

Abb. 6: Von vorne und von oben

2.4 3d-Schachbrett

Die Abbildung 7 zeigt ein 3d-Schachbrett.

Abb. 7: 3d-Schachbrett

In einem 3d-Schachbrett haben Würfel mit gemeinsamer Seitenfläche ungleiche Farbe. Würfel mit nur gemeinsamer Kante haben gleiche Farbe und Würfel mit nur gemeinsamer Ecke ungleiche Farbe.

In der Situation der Abbildungen 5 und 6 haben Würfel immer nur eine Kante gemeinsam.

Daher bilden in einem 3d-Schachbrett die Mittelpunkte der Würfel gleicher Farbe, zum Beispiel die Mittelpunkte aller weißen Würfel, ein flächenzentriertes kubisches Gitter.

3 Dreieckige Basis

Die Abbildung 8 zeigt das Minimalmodell für den Fall einer dreieckigen Basis.

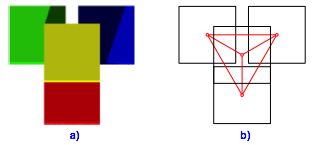
Abb. 8: Dreieckige Basis

Die Würfelmittelpunkte müssen die Ecken eines regelmäßigen Tetraeders bilden (Abb. 8b). Dieser Tetraeder hat die Höhe 1. Für die rote Kantenlänge x des Tetraeders ergibt sich:

(3)

Die Abbildung 9 zeigt die Basis und den Tetraeder.

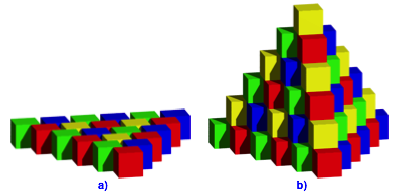
Abb. 9: Basis und Tetraeder

Die Abbildung 10 zeigt die Situation von der Seite und von oben.

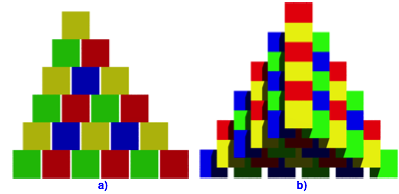
Abb. 10: Von der Seite und von oben