Hans Walser, [20220709]

Würfelstern

Idee und Anregung: Maik Bleckmann, Bremen

1 Worum geht es

Auf der Basis des Würfels wird aus Rhomben ein Stern gebaut. Clusterbildung. Verschiedene Sichten. Weiterführendes Ansetzen von Rhomben.

2 Konstruktion

Wir verbinden die Ecken des Würfels mit dem Mittelpunkt. Dadurch entstehen zwölf gleichschenklige Dreiecke (Abb. 1 und 2).

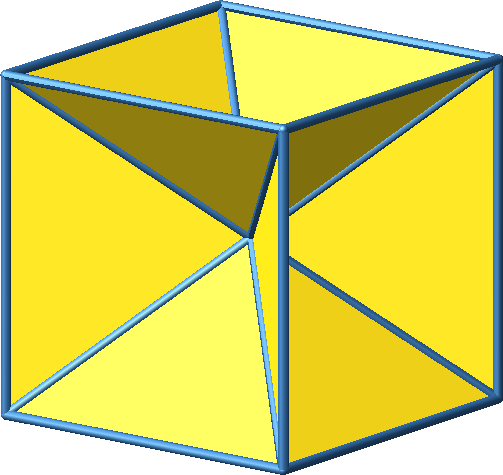
Abb. 1: Verbindung mit Mittelpunkt

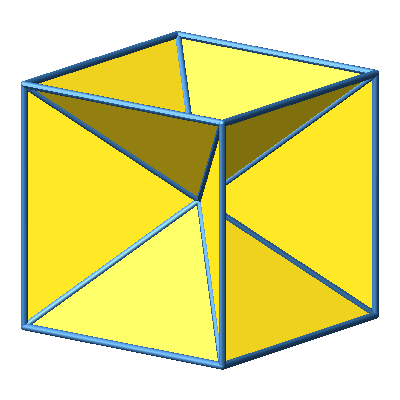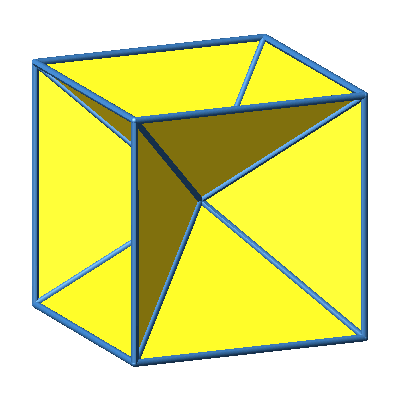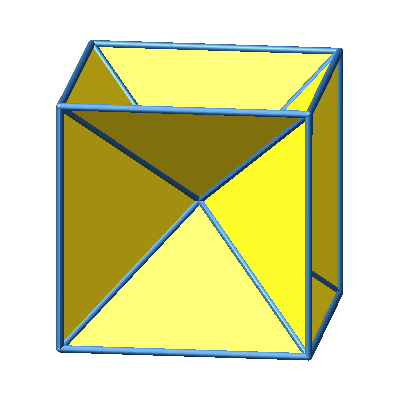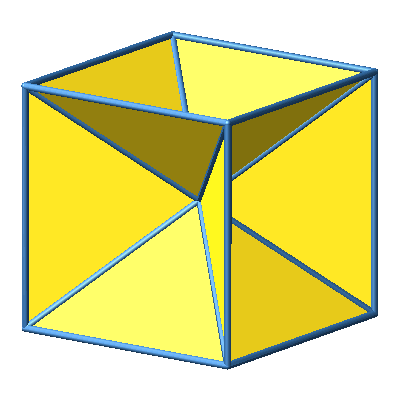
Abb. 2: Verbindung mit Mittelpunkt

Die Abbildung 3 zeigt ein Papiermodell dazu (Bauanleitung hier).

Abb. 3: Papiermodell

3 Dreieck und Rhombus

Ein einzelnes gleichschenkliges Dreieck passt in ein Rechteck im Seitenverhältnis des DIN-Formates (Abb. 4a). Der Winkel an der Spitze misst:

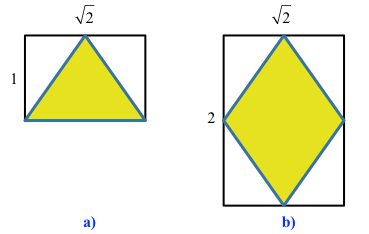
Abb. 4: Dreieck und Rhombus

Durch Verdoppelung nach unten entsteht ein Rhombus (Abb. 4b). Auch dieser Rhombus passt in ein Rechteck im Seitenverhältnis des DIN-Formates.

4 Würfelstern

Wir verdoppeln nun die Dreiecke der Abbildung 1 und 2 nach außen. Dadurch entsteht ein aus zwölf Rhomben zusammengesetzter Stern (Abb. 5 und 6).

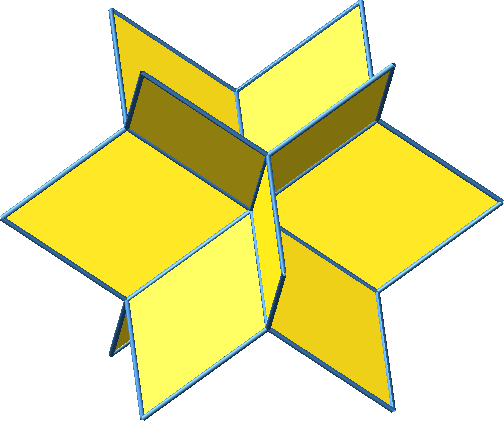
Abb. 5: Würfelstern aus zwölf Rhomben

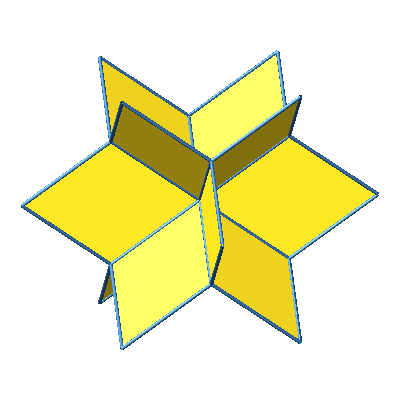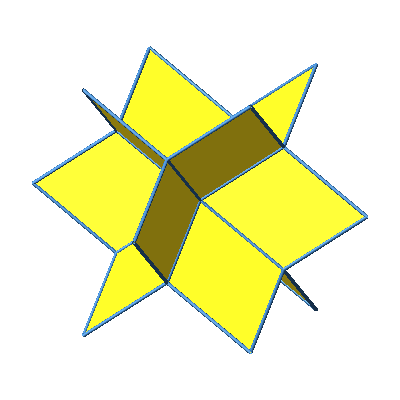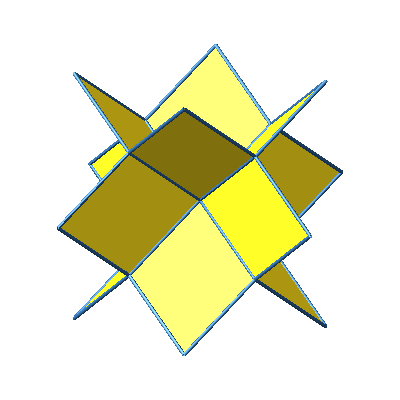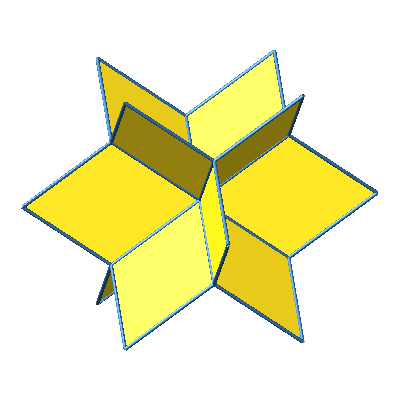
Abb. 6: Würfelstern

5 Spezielle Sichten

Die Abbildung 7a zeigte eine allgemeine Sicht auf einen Würfel. Es gibt nun aber drei spezielle Sichten auf einen Würfel.

(1) Wir können frontal auf eine Seitenfläche schauen (Abb. 7b). Der Umriss der Figur ist ein Quadrat.

(2) Wir können den Würfel über eine Kante ansehen (Abb. 7c). Der Umriss der Figur ist ein Rechteck im Seitenverhältnis des DIN-Formates. Wir sehen zwei Seitenflächen, die als Rechtecke im DIN-Format erscheinen.

(3) Wir können den Würfel über eine Ecke ansehen (Abb. 7d). Der Umriss der Figur ist ein regelmäßiges Sechseck. Wir sehen drei Seitenflächen, die als Rhomben mit einem spitzen Winkel 60° erscheinen.

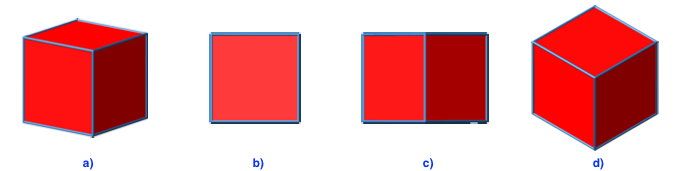
Abb. 7: Spezielle Sichten auf einen Würfel

6 Cluster

Die Abbildung 8 zeigt eine würfelförmige Anordnung von 3×3×3 = 27 Würfelsternen in verschiedenen Ansichten.

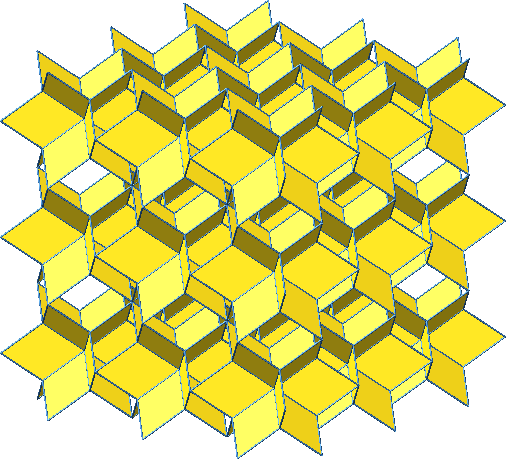
Abb. 8a: Allgemeine Ansicht

Abb. 8b: Frontale Sicht

Abb. 8c: Sicht über eine Kante

Abb. 8d: Sicht über eine Ecke

7 Weitere Rhomben ansetzen

Wir können dem Würfelstern der Abbildungen 5 und 6 weitere Rhomben ansetzen (Abb. 9 und 10).

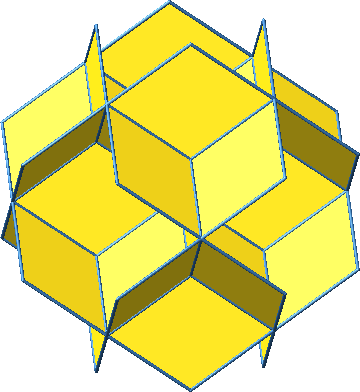
Abb. 9: Weitere Rhomben

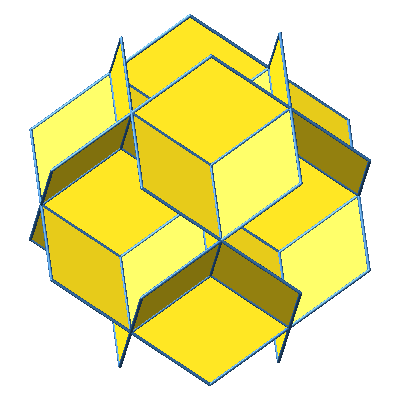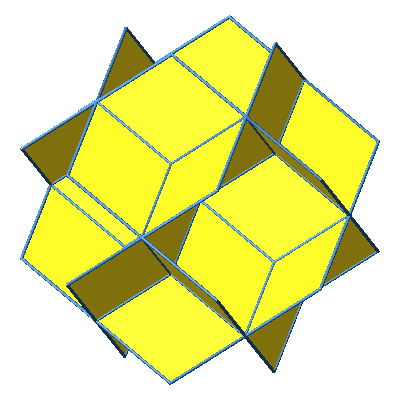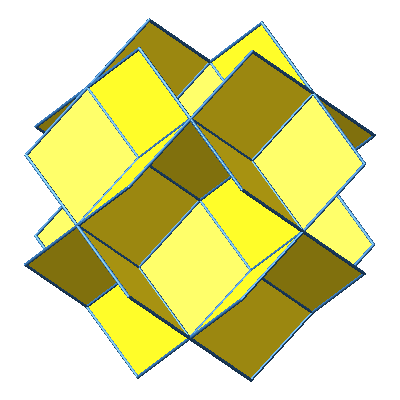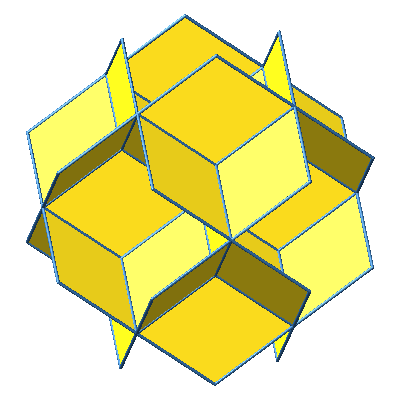
Abb. 10: Weitere Rhomben

8 Deckeln

Wir können schließlich die offensichtlichen Hohlräume mit je vier weiteren Rhomben deckeln (Abb. 11 und 12). Die entstehende Figur ist aus sechs Rhombendodekaedern zusammengesetzt. Die Zentren der Rhombendodekaeder bilden ein Oktaeder.

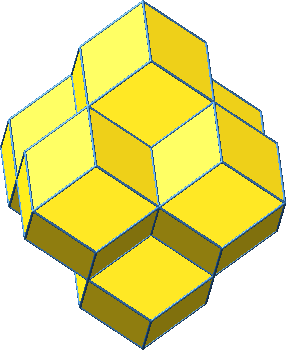
Abb. 11: Sechs Rhombendodekaeder

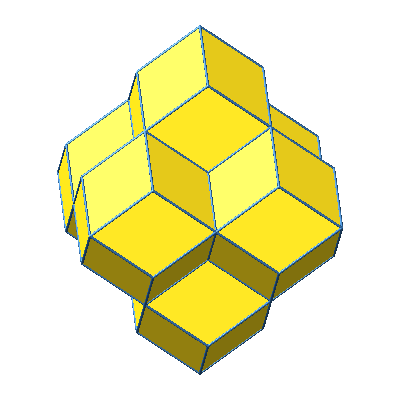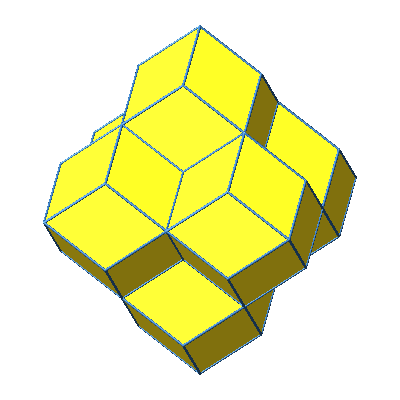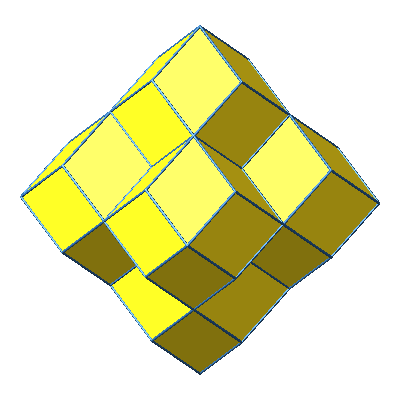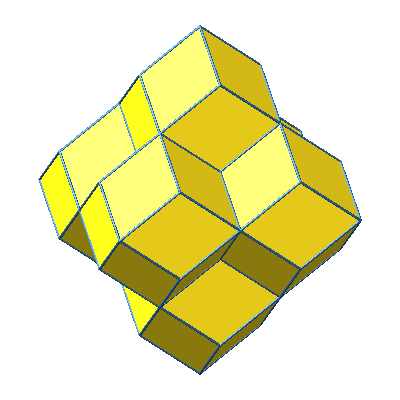
Abb. 12: Sechse Rhombendodekaeder in Bewegung

Die Abbildung 13 zeigt simultan die einzelnen Standbilder der Animation der Abbildung 12.

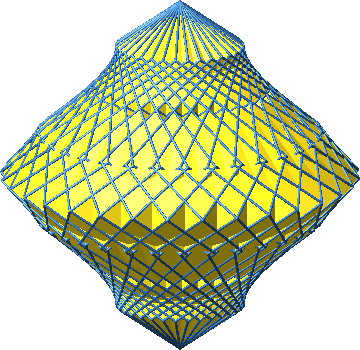
Abb. 13: Lampion

Websites

Hans Walser: Kantenmodell des Würfels und des Tetraeders

http://www.walser-h-m.ch/hans/Miniaturen/K/Kantenmodell_Wuerfel/Kantenmodell_Wuerfel.htm

Hans Walser: Kuboktaeder-Stern

http://www.walser-h-m.ch/hans/Miniaturen/K/Kuboktaeder-Stern/Kuboktaeder-Stern.html

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.