Hans Walser, [20191204]
WŸrfeltransformation
Anregung: Boris Odehnal, Wien
1 Worum geht es?
Manipulation am WŸrfel. Wir erhalten das regulŠre Dodekaeder, das Rhombendodekaeder, den Kemper-Stern und den Ikosaeder-Stern.
2 WŸrfel und Ebenen
2.1 Drehsinn der WŸrfelkanten
Wir versehen die Kanten eines WŸrfels mit einem Drehsinn gemŠ§ Abbildung 1.
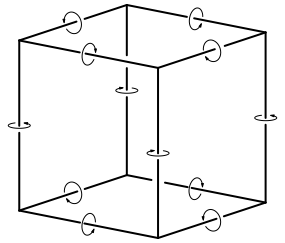
Abb. 1: Drehsinn der WŸrfelkanten
Ist der Drehsinn konsistent?
Wie kann die Drehung mit ZahnrŠdern (KegelrŠdern) realisiert werden? (Tipp: diagonalen).
Die Abbildung 2 zeigt die zugehšrigen Drehvektoren. Die Pfeilspitzen liegen in den Ecken eines einbeschriebenen Tetraeders.
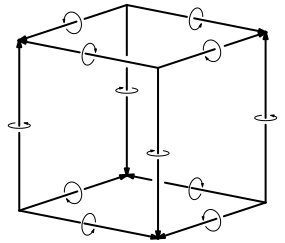
Abb. 2: Drehvektoren
2.2 Ebenen
Wir bringen nun an jeder WŸrfelkante ein Rechteck in Form eines halben Quadrates an (Abb. 3), so dass die Rechtecke auf der WŸrfeloberflŠche liegen. Wir erhalten ein unregelmŠ§iges Dodekaeder.
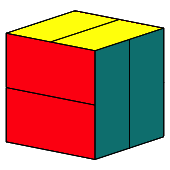
Abb. 3: Halbe Quadrate
2.3 Drehen der Ebenen
Nun drehen wir die Ebenen der halben Quadrate je um die zugehšrige WŸrfelkante im Drehsinn der Abbildungen 1 und 2 um denselben Winkel. Die Abbildung 4 zeigt die entstehende Schnittfigur.
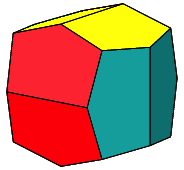
Abb. 4: Drehen und Verschneiden
Es entsteht ein unregelmŠ§iges Dodekaeder.
Wenn wir weiterdrehen, ergibt sich ein regelmŠ§iges Dodekaeder (Abb. 5).
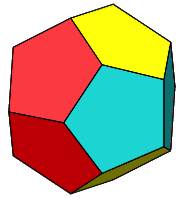
Abb. 5: RegelmŠ§iges Dodekaeder
Die Abbildung 6 zeigt eine weitere Situation (unregelmŠ§iges Dodekaeder).
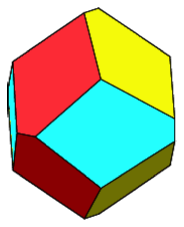
Abb. 6: UnregelmŠ§iges Dodekaeder
Schlie§lich ergibt sich ein Rhombendodekaeder (Abb. 7).
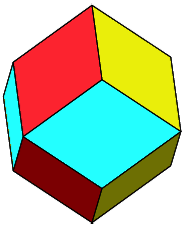
Abb. 7: Rhombendodekaeder
Was ergibt sich, wenn wir noch weiter drehen?
2.4 ZurŸckdrehen
Wir kšnnen natŸrlich auch, ausgehend von der Situation der Abbildung 3, zurŸckdrehen, also im Gegensinn der in den Abbildungen 1 und 2 angegebenen Drehsinne. Die Abbildung 8 zeigt eine solche Position.
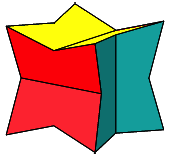
Abb. 8: ZurŸckdrehen
Wir erhalten ein nicht konvexes Dodekaeder mit nicht konvexen FŸnfecken als SeitenflŠchen.
Die Abbildung 9 zeigt als Sonderfall den Kemper-Stern (Carl Kemper, 1881-1957, Bildhauer und Architekt, Dornach).
Abb. 9: Kemper-Stern
Die SeitenflŠchen des Kemper-Sterns sind gleichseitige FŸnfecke, welche aus dem regulŠren FŸnfeck gemŠ§ Abbildung 10 erhalten werden kšnnen.
Abb. 10: Das nicht-konvexe halbregulŠre FŸnfeck
Die Abbildung 11 zeigt ein Papiermodell des Kemper-Sterns.
Abb. 11: Papiermodell
Beim Weiterdrehen werden die acht Spitzen des Sterns immer schlanker (Abb. 12).
Abb. 12: Schlanke Spitzen
Bald sind sie dŸnn wie der Suppenkaspar und bestehen nur noch aus Linien. Dies sind die Raumdiagonalen des WŸrfels (Abb. 13).
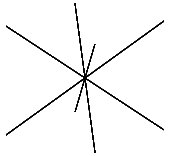
Abb. 13: WŸrfeldiagonalen
2.5 †berdrehen
Wenn wir jetzt noch weiter zurŸckdrehen, entsteht eine sternartige Figur mit Selbstdurchdringung (Abb. 14).
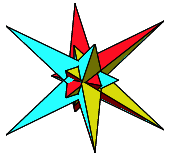
Abb. 14: Selbstdurchdringung
Schlie§lich ergibt sich der Ikosaeder-Stern, ein Poinsot-Kšrper (Louis Poinsot, 1777-1859) (Abb. 15).
Abb. 15: Ikosaeder-Stern
Die Animation zeigt den Transformationsvorgang vom Ikosaeder-Stern bis zum Rhombendodekaeder.
Animation: Transformation
3 Raumpackung
Wir fŠrben eine Raumpackung aus WŸrfeln schachbrettartig (3d-ãSchachbrettÒ) gelb und rot. Bei den gelben WŸrfeln drehen wir auswŠrts, bei den roten WŸrfeln gleich viel einwŠrts. So entsteht eine Packung aus zwei Kšrpern. Die Abbildung 16 zeigt als Beispiel eine Packung aus regulŠren Dodekaedern und Kemper-Sternen.
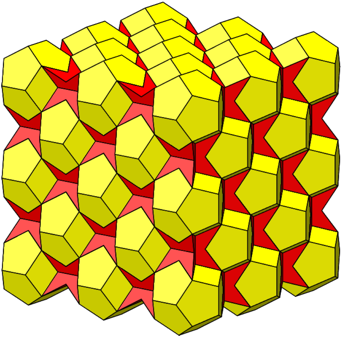
Abb. 16: Raumpackung
Website
Carl Kemper (abgerufen 27.11.2019)
http://biographien.kulturimpuls.org/detail.php?&id=169