Hans Walser, [20140507a]
Wrfelverdoppelung mit Stern und Spirale
1 Worum geht es?
Die volumenm§ige Wrfelverdoppelung ist mit Zirkel und Lineal nicht durchfhrbar. Es geht aber mit anderen Methoden, so auch mit einer geeigneten Spirale und eine regelm§igen 3-Stern.
2 Spirale und Stern
Wir verwenden die logarithmische Verdoppelungsspirale, deren Abstand vom Zentrum sich mit einem Umlauf verdoppelt (Abb. 1a). Die Spirale hat die Parameterdarstellung:
![]()

Abb. 1: Spirale und Stern
Die Abbildung 1b zeigt den Stern. Er erinnert an das Logo einer Automarke.
3 Vorgehen zur Wrfelverdoppelung
Wir wollen den Wrfel der Abbildung 2 volumenm§ig verdoppeln.
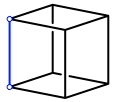
Abb. 2: Ausgangswrfel
Als Referenzlnge nehmen wir die senkrechte blau eingezeichnete Kante.
3.1 bertragung auf Stern
Wir bertragen die Referenzlnge auf den senkrechten Ast des Sternes (Abb. 3). Zugleich setzen wir den Stern mittig auf die Spirale.
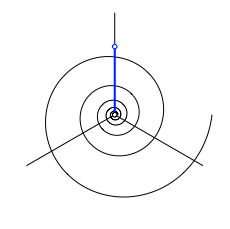
Abb. 3: Referenzlnge, Stern und Spirale
Wir sehen, dass der obere Punkt der Referenzlnge nicht auf der Spirale liegt.
3.2 Drehen der Spirale
Nun drehen wir die Spirale im Uhrzeigersinn. Dadurch wird sie scheinbar gr§er. Wir drehen so lange, bis sie durch den oberen Punkt der Referenzlnge geht (Abb. 4).
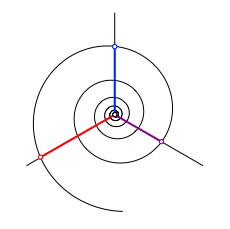
Abb. 4: Gedrehte Spirale
Auf den beiden anderen sten des Sterns haben wir nun eine Strecke (rot), welche etwas lnger ist als die blaue Referenzstrecke sowie eine Strecke (lila), welche etwas krzer ist als die blaue Referenzstrecke.
Die rote Strecke ist die Referenzlnge fr den volumenm§ig doppelt so gro§en Wrfel (Abb. 5a), die lila Referenzlnge gehrt zum volumenm§ig halb so gro§en Wrfel (Abb. 5b).
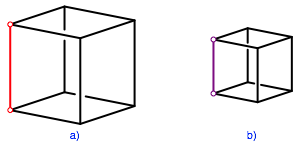
Abb. 5: Doppelt und halb so gro§es Volumen
4 Beweis
Der Beweis geht wie folgt. Bei einer logarithmischen Spirale wchst der Radius exponentiell mit dem Drehwinkel.
Fr eine volle Drehung
haben wir den Wachstumsfaktor 2. Fr eine Dritteldrehung ergibt sich der Faktor
![]() . Das ist genau der Faktor, den wir als Lngenvernderungsfaktor
fr die Volumenverdoppelung brauchen.
. Das ist genau der Faktor, den wir als Lngenvernderungsfaktor
fr die Volumenverdoppelung brauchen.
Kompetenzkontrolle: Welche Automarke wre in einer 5d-Hyperwelt passend?