Hans Walser, [20200528]

Würfelverdoppelung

Idee, Anregung und Farbgebung: Jo Niemeyer, Berlin

1 Worum geht es?

Einschiebeverfahren zur volumenmäßigen Verdoppelung eines Würfels.

2 Wie geht es?

Wir arbeiten mit einem unterteilten Zwölfeck (Abb. 1). Die sechs blauen Quadrate sind die Seitenflächen des Würfels, den wir verdoppeln wollen.

Abb. 1: Zwölfeck

Auf der Oberkante des Sockels wählen wir einen Punkt und verbinden ihn mit der Spitze des untersten Dreiecks im Zwölfeckmuster. Auf die Verbindungsgerade setzen wir ein Quadrat mit einer Ecke im gewählten Punkt. Das Quadrat ist gleich groß wie die Quadrate im Zwölfeckmuster (Abb. 2). Man kann es als Bodenstück des gegebenen Würfels interpretieren.

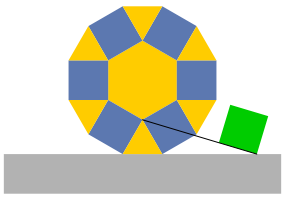
Abb. 2: Gerade und Quadrat

Nun verschieben wir den gewählten Punkt auf der Oberkante des Sockels (Abb. 3).

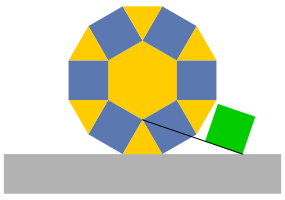
Abb. 3: Verschieben des Startpunktes

Wir verschieben weiter, bis die zweite untere Quadratecke beim Zwölfeckumriss ankommt (Abb. 4).

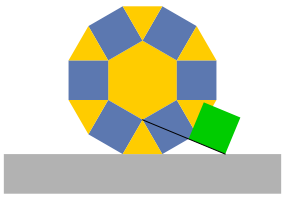
Abb. 4: Kontakt mit Zwölfeckumriss

Das freie Stück zwischen dem Kontaktpunkt und der Dreieckspitze ist die Kantenlänge des Würfels mit doppeltem Volumen.

In der Abbildung 5 ist ein Quadrat mit dieser Kante eingezeichnet. Man kann dieses als Bodenstück des gesuchten Würfels interpretieren.

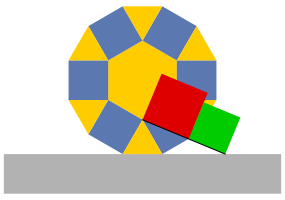
Abb. 5: Bodenstück des gesuchten Würfels

3 Im Raum

Die Abbildung 6 entspricht der Abbildung 5, aber in den Raum gelegt.

Abb. 6: Im Raum

Nun können wir den gegebenen und den gesuchten volumenmäßig doppelt so großen Würfel sichtbar machen (Abb. 7).

Abb. 7: Die beiden Würfel

Websites

Hans Walser: Würfelverdoppelung

www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelverdoppelung3/Wuerfelverdoppelung3.htm

Hans Walser: Würfelverdoppelung

www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelverdoppelung/Wuerfelverdoppelung.htm

Hans Walser: Würfelverdoppelung mit Stern und Spirale

www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelverdoppelung2/Wuerfelverdoppelung2.htm