Hans Walser, [20220208]

Würfelverdoppelung

1 Worum geht es?

Ein Würfel kann mit Zirkel und Lineal volumenmäßig weder verdoppelt noch halbiert werden. Mit anderen Hilfsmitteln geht es.

Im Folgenden eine Spielerei. Verdoppelung durch eine Folge von Halbierungen nach dem Muster:

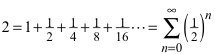
2 Konstruktion

Einem blauen Würfel setzen wir ein volumenmäßig halb so großen goldenen Würfel auf (Abb. 1 und 2). Der Skalierungsfaktor s für die Längen ist dabei:

Dem goldenen Würfel setzen wir einen halb so großen nun wieder blauen Würfel auf. Und so weiter und so fort. Der entstehende Turm ist volumenmäßig doppelt so groß wie der blaue Startwürfel. Bei einer Kantenlänge 1 des blauen Startwürfels hat der Turm die Höhe h:

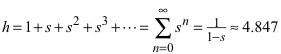
Abb. 1: Konstruktion

Abb. 2: Die Bäume wachsen nicht in den Himmel

3 Profil

Die Abbildung 3 zeigt den Turm von vorne. Die aufgetürmten Würfel passen in eine Pyramide. Deren Seitenflächen haben gegenüber der Horizontalen die Steigung m

und den Steigungswinkel:

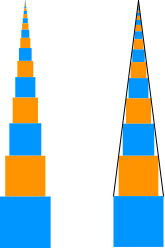
Abb. 3: Profil

4 Verdrehung

Wir verdrehen die aufgesetzten Würfel so, dass die senkrechten Kanten bündig mit den Seitenflächen des darunter stehenden Würfels sind (Abb. 4). Der Verdrehungswinkel ist:

Es kann (von oben gesehen) im Uhrzeigersinn, im Gegenuhrzeigersinn oder alternierend gedreht werden. Im alternierenden Fall sind alle blauen Würfel untereinander parallel, ebenso alle goldenen Würfel.

Abb. 4: Verdrehungen

Die Abbildung 5 zeigt die entsprechenden Sichten von oben.

Abb. 5: Sicht von oben

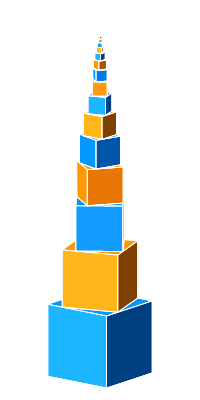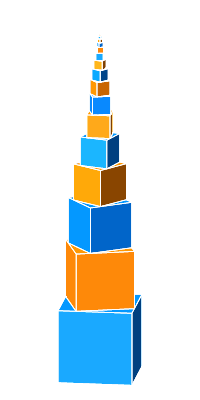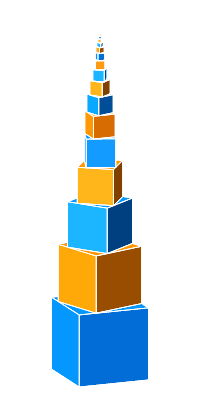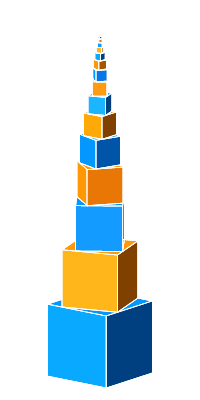
Abb. 6: Links- und Rechtsschraube

Websites

Hans Walser: Würfelverdoppelung

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelverdoppelung/Wuerfelverdoppelung.htm

Hans Walser: Würfelverdoppelung

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelverdoppelung3/Wuerfelverdoppelung3.htm

Hans Walser: Würfelverdoppelung

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelverdoppelung4/Wuerfelverdoppelung4.htm

Hans Walser: Würfelverdoppelung mit Stern und Spirale

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelverdoppelung2/Wuerfelverdoppelung2.htm