Hans Walser, [20220823]
Würfelwelt
1 Fragestellung
Wir legen eine Kugel so ein den berührenden Umwürfel, dass die Kugelachse durch zwei diametrale Würfelecken verläuft (Abb. 1 und 2).
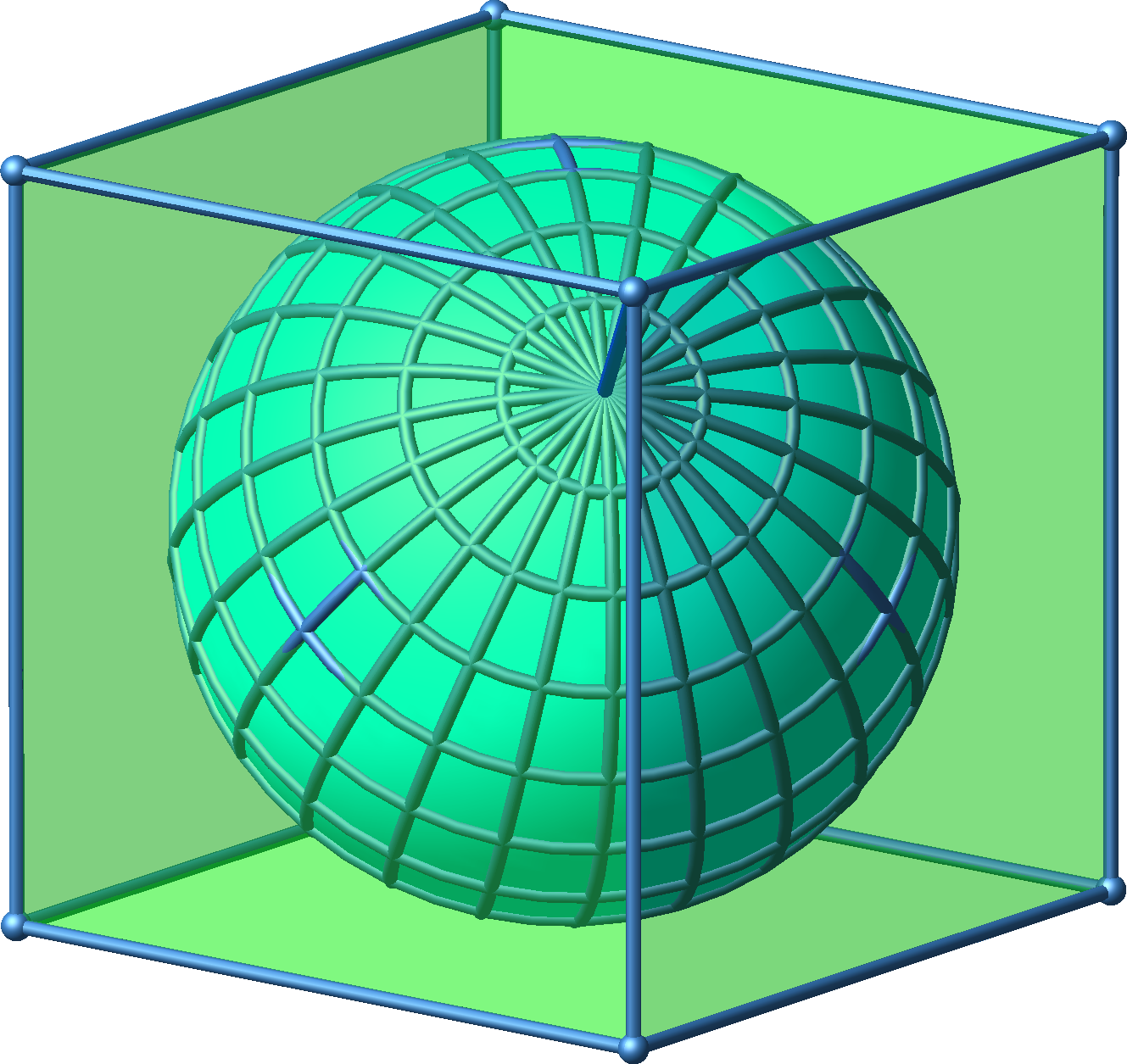
Abb. 1: Kugel im Umwürfel

Abb. 2: Spezielle Sicht
Wie sieht die Projektion (Zentralprojektion vom Mittelpunkt aus) der Netzlinien der Kugel (Maschenweite 15°) auf die Würfeloberfläche aus?
2 Bemerkungen
Es handelt sich um die sogenannte gnomonische Projektion.
Die Bilder von Großkreisen, in unserem Fall also Meridiane und Äquator, sind Geraden.
Die Bilder von Kleinkreisen, in unserem Fall also die Breitenkreise, sind Kegelschnitte.
3 Bild des Äquators
Das Bild des Äquators ist ein regelmäßiges Sechseck mit Eckpunkten in Kantenmitten des Würfels (Abb. 3).
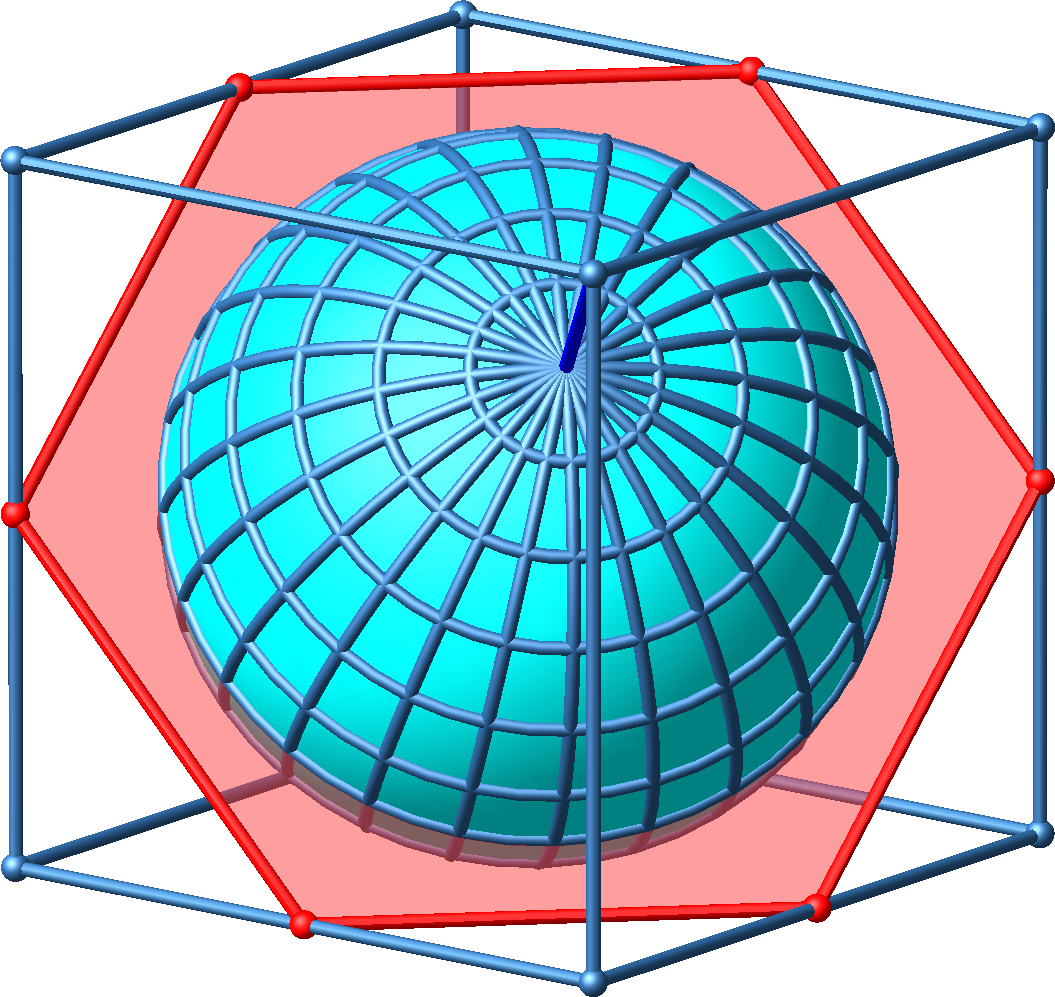
Abb. 3: Bild des Äquators ein Sechseck
4 Senkrechte Achse
Wir stellen nun die Achse senkrecht. Die Äquatorebene ist dann waagerecht. Weiter drehen wir um die senkrechte Achse so, dass wir den Würfel über eine Kante sehen (Abb. 4). Der Würfelumriss erscheint dann als Rechteck mit dem Seitenverhältnis √2 : 1. Die Raumdiagonale des Würfels, in der Abbildung 4 als senkrechte Strecke sichtbar, hat gegenüber der Kantenlänge des Würfels das Längenverhältnis √3 : 1.
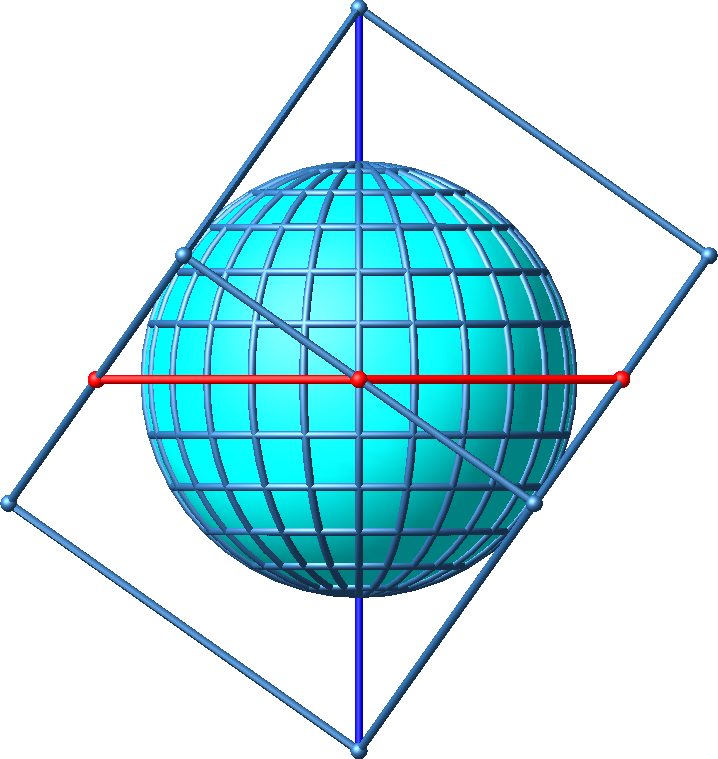
Abb. 4: Spezielle Sicht
5 Konstruktives Vorgehen
Aus Symmetriegründen sieht die gesuchte Projektion der Netzlinien auf allen sechs Seitenquadraten gleich aus. Wir konstruieren nun den Bildpunkt eines Kugelpunktes mit der gegebenen geografische Breite φ und der gegebenen geografischen Länge λ auf dem Seitenquadrat links oben in der Abbildung 4. Dieses Seitenquadrat ist in der Disposition der Abbildung 4 nur als Strecke sichtbar („projizierende Ebene“ in der Sprache der darstellenden Geometrie). Die Länge dieser Strecke ist die Diagonalenlänge der Seitenquadrate des Würfels.
5.1 Sichtbarmachung des Seitenquadrates
Da die Raumdiagonale des Würfels gegenüber der Seitenlänge das Längenverhältnis √3 : 1 hat, können wir den obersten Punkt in der Abbildung 4 mit Hilfe eines gleichseitigen Dreiecks konstruieren (Abb. 5). Damit kann dann auch der Umriss des Würfels gezeichnet werden. Der oberste Punkt ist das Bild des Nordpols bei unserer gesuchten Projektion, der unterste Punkt entsprechend das Bild des Südpols.
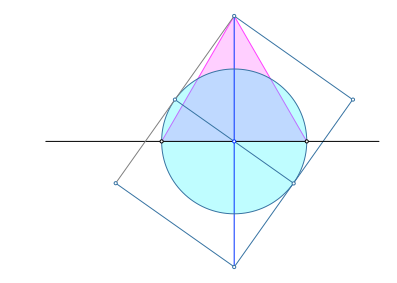
Abb. 5: Umriss des Würfels
Nun kann auch das gesuchte Seitenquadrat links oben sichtbar gemacht werden (durch Drehen um 90° um seine Diagonale, „Umlegen“ in der Sprache der darstellenden Geometrie) (Abb. 6).
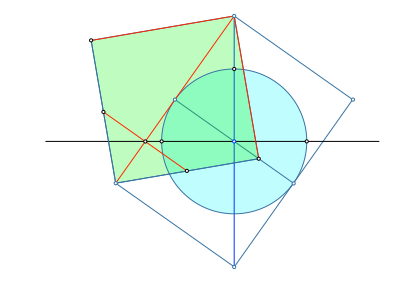
Abb. 6: Seitenquadrat
Mit den eingezeichneten roten Strecken hat es folgende Bewandtnis. Die drei roten vom obersten Punkt, dem Bild des Nordpols also, ausgehenden roten Linien sind Bilder von Meridianen. Wir legen die Quadratdiagonale als Bild des 0°-Meridians (Greenwich-Meridian) fest. Die roten Quadratseiten sind dann die Bilder der ±60°-Meridiane. Dies ist zunächst irritierend, da rein planimetrisch die Winkelabweichungen von der Diagonalen nur ±45° betragen. Ein Blick auf den Nordpol (Abb. 7) klärt den Sachverhalt. Wir sind in der sonderbaren Situation, dass der auf 120° verzerrte rechte Winkel des Seitenquadrates beim Bild des Nordpols den echten geografischen Längen entspricht.
Die kurze rote Strecke von Kantenmitte zu Kantenmitte ist das auf diesem Quadrat relevante Bild des Äquators.

Abb. 7: Blick auf den Nordpol
In der Abbildung 8 ist zusätzlich ein gleichschenkliges Hilfsdreieck mit dem Spitzenwinkel 120° und der Basis auf dem Bild des Äquators eingetragen. Dieses Dreieck werden wir für die Abtragung der geografischen Länge benötigen. Die 120° entsprechen dem für unser Seitenquadrat relevanten Bereich für die ±60°-Meridiane.
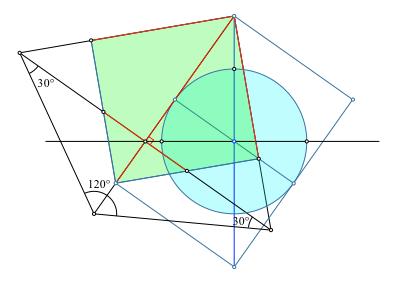
Abb. 8: Hilfsdreieck mit Öffnungswinkel 120°
5.2 Konstruktion eines allgemeinen Punktes
Wir beschreiben exemplarisch die Konstruktion des Bildes einen allgemeinen Punktes der gegebenen geografische Breite φ und geografischen Länge λ.
Zunächst zeichnen wir im Hilfsdreieck die geografische Länge λ gemäß Abbildung 9 ein. Dies führt uns auf dem (verlängerten) Bild des Äquators zum Fußpunkt des Bildes des zur geografischen Länge λ gehörenden Meridians. Dieses Meridianbild können wir nun einzeichnen.
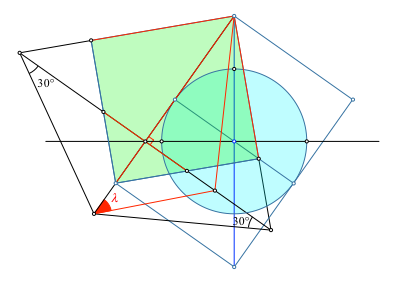
Abb. 9: Geografische Länge. Bild des Meridians
Wir drehen das Meridianbild, bis der Fußpunkt auf die Äquatorebene zu liegen kommt (Abb. 10).
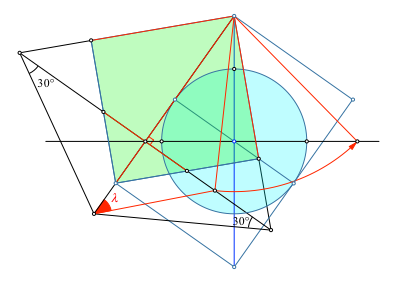
Abb. 10: Drehen des Meridianbildes
Nun können wir die geografische Breite φ einzeichnen und den zugehörigen Punkt auf dem gedrehten Meridianbild (Abb. 11).
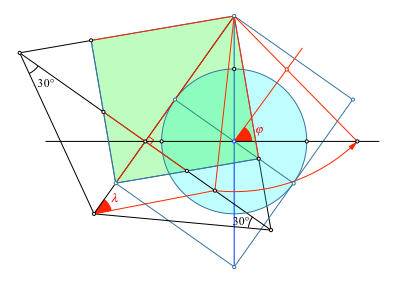
Abb. 11: Geografische Breite
Zurückdrehen liefert schließlich den gesuchten Bildpunkt (Abb. 12).
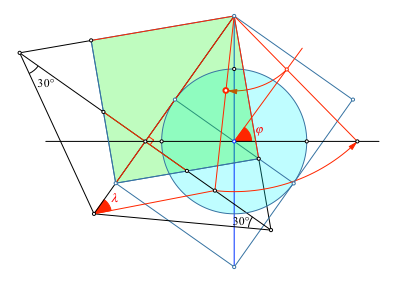
Abb. 12: Bildpunkt
6 Bild der Netzlinien
Die Bilder der Meridiane können wir einfach konstruieren.
Für die Bilder der Breitenkreise habe ich jeweils fünf Punkte der betreffenden geografischen Breite konstruiert und diese dann zu einem Kegelschnitt ergänzt. So ergibt sich das Bild der Netzlinien (Abb. 13).
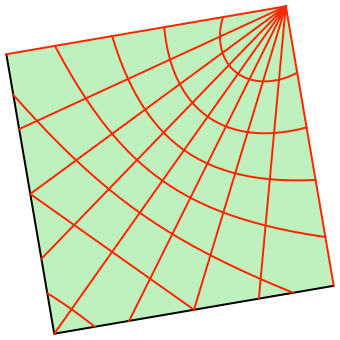
Abb. 13: Projektion auf eine quadratische Würfelseite
Die Bilder der Breitenkreise in Polnähe sind Ellipsen, in Äquatornähe Hyperbeln. Die Schnittstelle zwischen Ellipsen und Hyperbeln ist die geografische Breite arctan(√2) ≈ 54.7356°. Für diese geografische Breite (sie kommt im 15°-Raster nicht vor) ist das Bild des Breitenkreises eine Parabel.
7 Würfelabwicklungen
Die Abbildungen 14 und 15 zeigen zwei Würfelabwicklungen mit den Projektionen der Netzlinien.
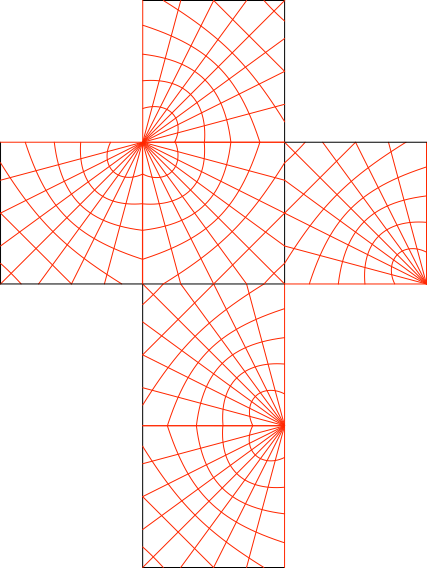
Abb. 14: Abwicklung lateinisches Kreuz

Abb. 15: Elegante Abwicklung
8 Flechtmodell
Mit den drei senkrechten Streifen der Abbildung 16 kann ein Flechtmodell hergestellt werden.

Abb. 16: Die drei Streifen
Die Abbildung 17 zeigt das Flechtmodell.

Abb. 17: Flechtmodell
Weblinks
Hans Walser: Würfelwelten
http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelwelten/Wuerfelwelten.htm