Hans Walser, [20070129a], [20130416], [20131014a]

WŸrfelwelten

1        Projektion vom Mittelpunkt aus

Wir projizieren die Erdkugel (Abb. 1a) vom Zentrum aus auf den umgebenden WŸrfel. Die Bilder der Meridiane sind Geraden, die Bilder der Breitenkreise sind Hyperbeln (auf den SeitenflŠchen des WŸrfels) und Kreise (auf Deckel und Boden des WŸrfels) (Abb. 1b).

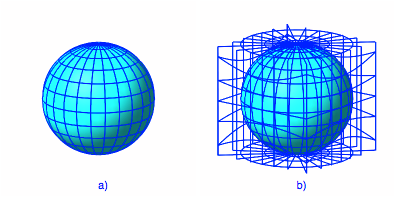
Abb. 1: Projektion auf den WŸrfel

Die Abbildung 2 zeigt den WŸrfel allein.

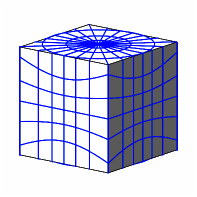
Abb. 2: WŸrfel

Nun fehlt noch das Bild der Kontinente. Die Abbildung 3 zeigt die Vorderseite des WŸrfels mit dem Punkt  im Zentrum.

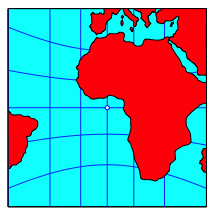
Abb. 3: Vorderseite

Es handelt sich hier um eine so genannte gnomonische Projektion.

2        WŸrfelmodelle

Wir kšnnen auf verschiedene Weise nun einen WeltenwŸrfel als Papiermodell herstellen.

2.1      Flechtmodell

Aus drei Streifen kann ein Flechtmodell geflochten werden. Die Abbildung 4 zeigt die drei Streifen. Zuerst sind drei Streifen zu schneiden, dann die Kanten vorzufalten und dann kommt das Flechten. Profis falten vor dem Schneiden, so kšnnen alle drei Streifen simultan gefaltet werden. Das Flechten braucht etwas Geduld; die Kontinente helfen dabei.

 

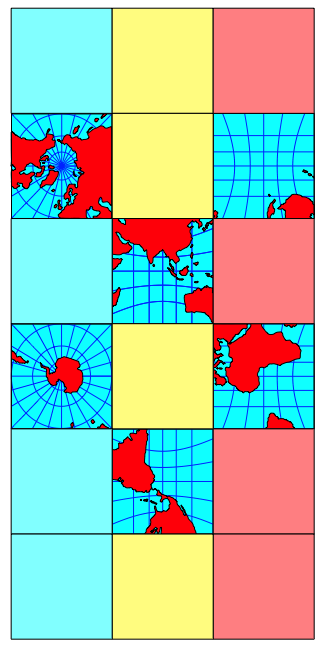
Abb. 4: Die drei Streifen fŸr das Flechtmodell

In der Abbildung 5 das Flechtmodell in zwei Ansichten.

      

Abb. 5: Flechtmodell

2.2      Abwicklung

Die Abbildung 6 zeigt eine Abwicklung des WŸrfels.

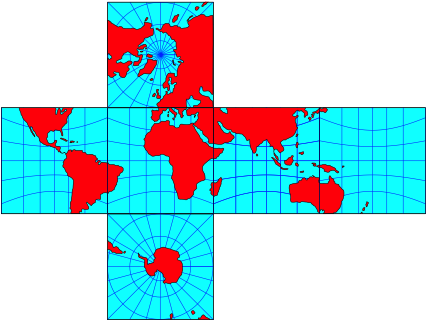
Abb. 6: WŸrfelabwicklung

FŸr Bastelzwecke dieselbe Abwicklung als Schnittmuster mit Klebelaschen (Abb. 7).

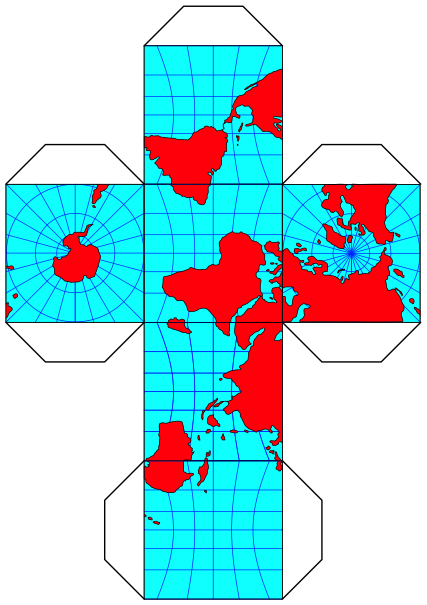
Abb. 7: Mit Klebelaschen

3        Spielereien

3.1      3d-Kreuz

Mit etwas Geduld kann aus Streifen der Abbildung 4 ein 3d-Kreuz geflochen werden (Abb. 8). Dabei sind bei allen KantenŸbergŠngen die Kontinente zusammenhŠngen, auch bei den konkaven Kanten. FŸr das Modell braucht es 5 Streifensets, also insgesamt 15 Streifen.

Abb. 8: 3d-Kreuz

3.2      Mehrfachwelten

Auf wie viele Arten kann aus dem Atlas der Abbildung 9 ein Schnittmuster fŸr eine WŸrfelwelt herausgeschnitten werden?

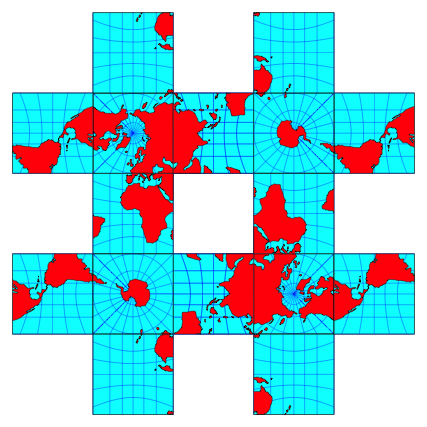
Abb. 9: Mehrfachwelt

3.3      Rhomben

Wir kšnnen die 6 Seitenquadrate auf zwei Arten zu 60¡-Rhomben verzerren (Abb. 10).

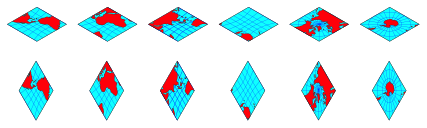
Abb. 9: Rhomben

Damit erhalten wir Baumaterial zu weiteren Figuren.

ZunŠchst eine isometrische Darstellung der WŸrfelwelt (Abb. 11).

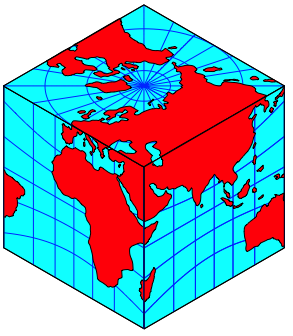
Abb. 11: Die Welt als WŸrfel und Vorstellung

Von da ist es nicht mehr weit zum Stern (Abb. 12). Wir sehen die halbe Welt doppelt.

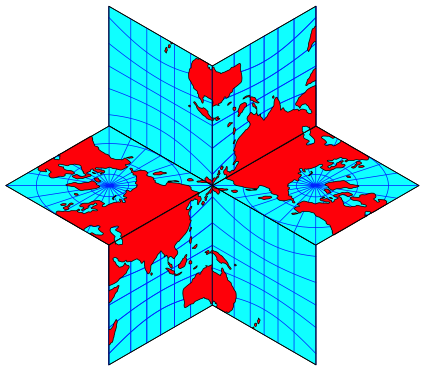
Abb. 12: Stern

Wir kšnnen auch die ganze Welt doppelt sehen (Abb. 13).

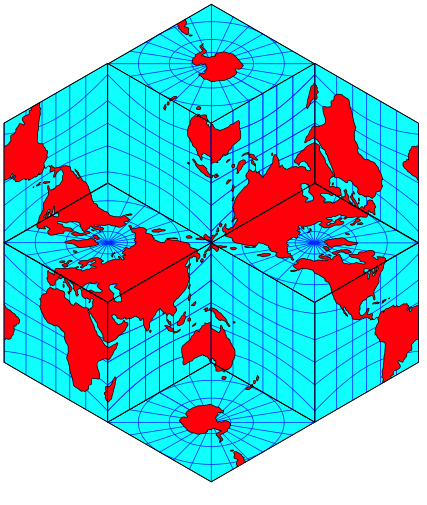
Abb. 13: Doppelte Welt

Wir kšnnen das zu einem Parkett ausweiten (Abb. 14).

Abb. 14: He nu so de