Hans Walser, [20090505a]
Wurzeln aus der Einheitsmatrix
1
Worum es geht
Wir suchen 2,2-Matrizen
X mit der Eigenschaft:
Dabei ist E die Einheitsmatrix.
Die Lšsungen X werden als Abbildungsmatrix einer linearen Abbildung
interpretiert. Die so entstehenden Abbildungen haben die Eigenschaft, dass ihre
zweimalige Anwendung die IdentitŠt ist.
1.1
Analogie zu reellen Zahlen
Die Gleichung 
hat die beiden
Lšsungen 
und 
. Die Frage ist nun, wie viele Lšsungen es im Falle von
2,2-Matrizen gibt.
2
Beispiele
Triviale Beispiele:
Weitere Lšsungen sehen
wir bald:
3
Ansatz
Wir arbeiten fŸr X mit dem Ansatz:
Damit ist:
Es ergeben sich die
vier Gleichungen:
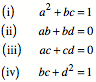
Wegen 
ist 
:
4
Fallunterscheidung
Nun eine etwas mŸhsame
Fallunterscheidung:
Fall 1: 
Fall 2: 
(symmetrische
Matrix)
Fall 3: 
Fall 4: 
Fall 5: 
(symmetrische
Matrix)
Fall 6: 
4.1
Fall 1
Aus (i) folgt 
und aus (ii)
folgt 
. Wir erhalten die zweiparametrige Lšsungsschar:
Es ist 
. FŸr die Eigenwerte erhalten wir 
und 
mit den
Eigenvektoren:
und 
Die lineare Abbildung
mit der Matrix X ist eine
SchrŠgspiegelung, deren Spiegelachse und Spiegelrichtung durch die Eigenvektoren
und 
gegeben sind.
Beispiel: FŸr 
und 
ergibt sich die
Matrix
mit den Eigenvektoren:
und 
In der nachfolgenden
Figur ist das Urbild grŸn, das Bild rot, die Spiegelachse blau und
die Spiegelrichtung
magenta eingetragen.
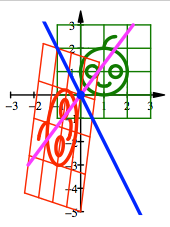
SchrŠgspiegelung
4.2
Fall 2
Wir haben eine
symmetrische Matrix. Aus 
folgt 
. Die Matrix
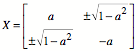
hat die Determinante 
, die Eigenwerte 
und 
und die
Eigenvektoren:
und 
Die beiden
Eigenvektoren sind orthogonal, wir haben also eine gewšhnliche Geradenspiegelung.
Beispiel: FŸr 
ergibt sich die
Matrix
mit den Eigenvektoren:
und 
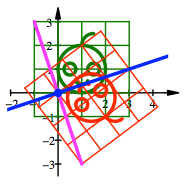
Geradenspiegelung
4.3
Fall 3
Wegen (i) ist 
, wegen (ii) folgt 
. Wir erhalten also die beiden Lšsungsscharen:
und 
Die erste Matrix hat
die Determinante 
, die Eigenwerte 
und 
und die
Eigenvektoren:
und 
Die zweite Matrix hat
ebenfalls die Determinante 
, die Eigenwerte 
und 
, aber die Eigenvektoren:
und 
FŸr 
ergibt sich in
diesen beiden FŠllen:
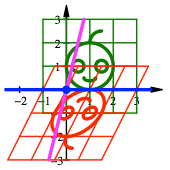
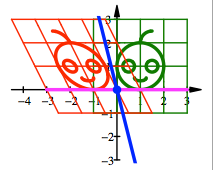
SchrŠgspiegelungen
4.4
Fall 4
Wegen (i) ist 
, wegen (iii) ist 
. Wir erhalten also die beiden Lšsungsscharen:
und 
Die erste Matrix hat
die Determinante 
, die Eigenwerte 
und 
und die
Eigenvektoren:
und 
Die zweite Matrix hat
ebenfalls die Determinante 
, die Eigenwerte 
und 
, aber die Eigenvektoren:
und 
FŸr 
ergibt sich in
diesen beiden FŠllen:
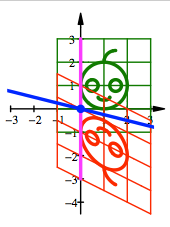
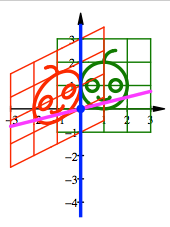
SchrŠgspiegelungen
4.5
Fall 5
Wegen (i) ist 
, wegen (iv) haben wir 
. Dies fŸhrt zu den vier Lšsungen:
Die erste dieser
Lšsungen ist die IdentitŠt, die zweite die Punktspiegelung am Ursprung, die
dritte die Spiegelung an der x-Achse und
die vierte die Spiegelung an der y-Achse.
4.6
Fall 6
Wegen (i) ist dann 
, also 
. Weiter ist wegen (iv) 
, also 
. Wir erhalten die Lšsung:
Die Matrix hat die
Determinante 
, die Eigenwerte 
und 
und die Eigenvektoren:
und 
Beispiel: FŸr 
ergibt sich die
Abbildungsmatrix:
Die Abbildung sieht so
aus:
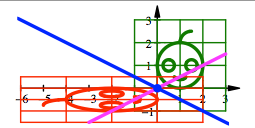
SchrŠgspiegelung
5
Zusammenfassung
á
: 
, 
, IdentitŠt
á
: 
, 
, Spiegelung am Ursprung
á
: 
, Geradenspiegelung oder SchrŠgspiegelung