Hans Walser, [20210730]

Wurzelpyramide

0 Worum geht es?

Pyramide auf der Basis der Wurzelspirale. Exemplarisches Vorgehen

1 Die Wurzelspirale

Die Abbildung 1a zeigt die ersten fünf Schritte der Wurzelspirale. Sie besteht aus rechtwinkligen Dreiecken, deren eine Kathete die konstante Länge 1 hat. Die andere Kathete, die auch Hypotenuse des vorhergehenden Dreiecks ist, hat der Reihe nach die Längen:

. (1)

Nach 16 Schritten wird beinahe eine volle Runde erreicht. Nachher beginnen die Überlappungen.

Abb. 1: Wurzelspirale

In der Abbildung 2 sind die ersten 100 Dreiecke gezeichnet. Die Spirale nähert sich einer archimedischen Spirale mit dem Abstand zwischen zwei Durchgängen an (Walser 2004). Dies kann an den mit Vielfachen von markierten Koordinatenachsen verifiziert werden.

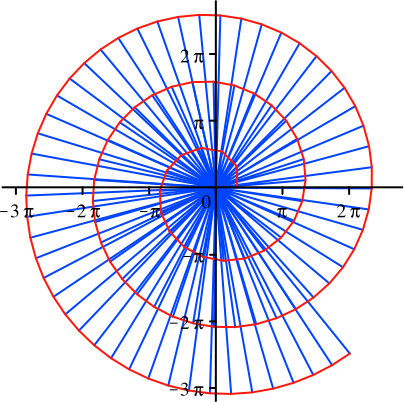
Abb. 2: 100 Dreiecke

2 Die Wurzelpyramide

Wir konstruieren exemplarisch eine Wurzelpyramide mit der Schlüsselzahl acht. Als Grundfläche nehmen wir die ersten acht Dreiecke der Wurzelspirale (grün in Abb. 3). Bei acht Dreiecken ergeben sich neun blaue Speichen (Zaunpfahlproblem). Diese haben der Reihe nach die Längen:

(2)

Die zweitletzte Speichenlänge ist die Quadratwurzel aus der Schlüsselzahl acht.

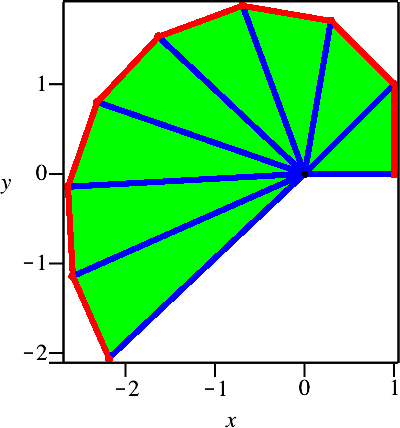
Abb. 3: Grundfläche

Die Abbildung 4 zeigt dasselbe in einem Schrägbild.

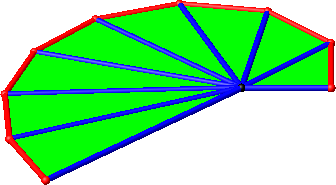
Abb. 4: Schrägbild

Nun setzen wir im Zentrum eine senkrechte Stange (Abb. 5) der Länge:

(3)

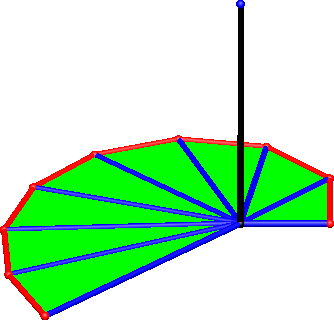
Abb. 5: Mast

Von der Spitze dieser Stange aus zeichnen wir Schrägkanten zu den Eckpunkten der Grundfläche (Abb. 6). Die Pyramide nimmt Form an.

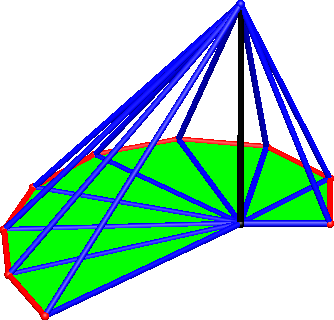
Abb. 6: Schrägkanten

Die Längen der Schrägkanten können wir mit den Stützdreiecken (gelb Abb. 7) berechnen. Diese Stützdreiecke sind rechtwinklige Dreiecke mit der senkrechten Stange als der einen und den Speichen als die jeweilige andere Kathete.

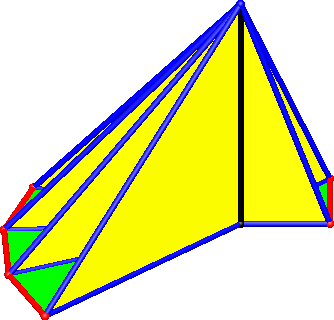
Abb. 7: Stützdreiecke

Für die jeweilige Hypotenuse, also die Länge der Schrägkante, erhalten wir der Reihe nach:

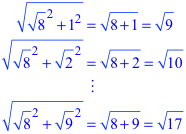(4)

Die erste Zahl von (4) ist die letzte Zahl von (1).

Nun setzen wir das Dach auf, beginnend mit dem kleinste Dachdreieck (rot in Abb. 8).

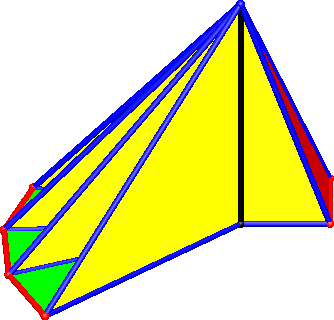
Abb. 8: Erste Dachdreieck

Dieses erste rote Dachdreieck hat die Seitenlängen:

(5)

Es ist also rechtwinklig, und zwar ist es genau das erste an die grünen Dreiecke in der Abbildung 3 anschließende Dreieck der Wurzelspirale. Dieser Sachverhalt hat mich bewogen, die vorliegende Studie zu schreiben.

Das gesamte Dach (Abb. 9) besteht aus den acht an die grünen Dreiecke der Abbildung 3 anschließenden Dreiecke der Wurzelspirale (Abb. 10).

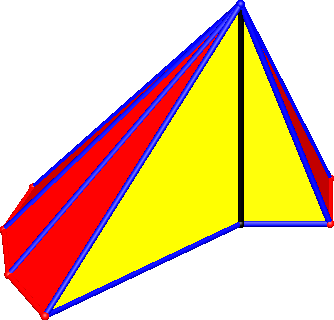
Abb. 9: Gesamtes Dach

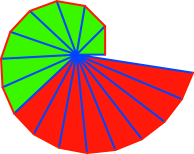
Abb. 10: Anordnung in der Wurzelspirale

Die Abbildung 11 gibt einen Blick ins Innere der Wurzelpyramide, die Abbildung 12 ist eine dazu passende Animation. Die Abbildung 13 zeigt ein Papiermodell.

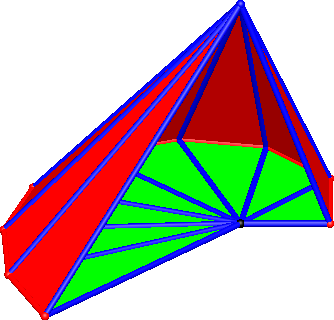
Abb. 11: Blick ins Innere

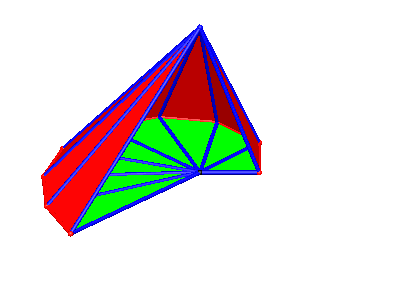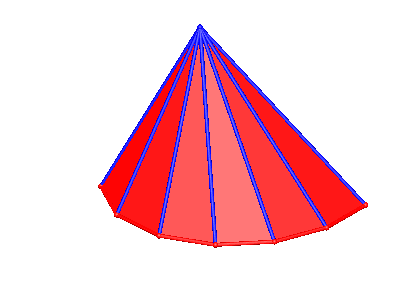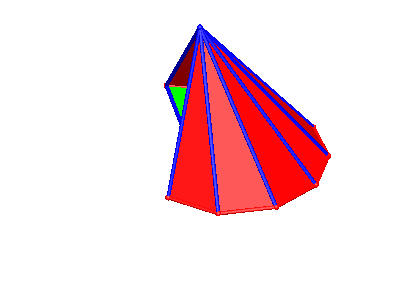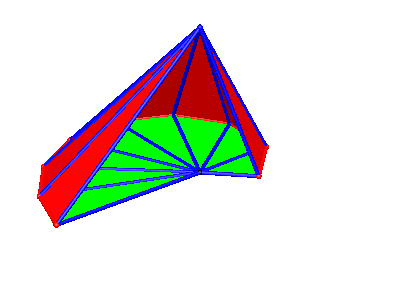
Abb. 12: Drehen um den Mast

Abb. 13: Papiermodell

3 Allgemein

Wir können die von uns verwendete Schlüsselzahl acht durch irgendeine natürliche Zahl ersetzen. In der Animation (Abb. 14) laufen die Schlüsselzahlen von null bis 25. Die Wurzelpyramide nimmt für wachsende Schlüsselzahlen eine schneckenförmige Gestalt an.

Abb. 14: Allgemein

Literatur

Walser, Hans (2004): Pythagoras, eine archimedische Spirale und eine Approximation von π. Praxis der Mathematik, 46, 287-288.

Websites

Hans Walser: Wurzelspirale

http://www.walser-h-m.ch/hans/Miniaturen/W/Wurzelspirale/Wurzelspirale.htm

Hans Walser: Wurzelspiralen

http://www.walser-h-m.ch/hans/Miniaturen/W/Wurzelspiralen/Wurzelspiralen.htm