Hans Walser, [20211220]
Wurzelrechtecke
1 Worum geht es?
Rechtecke mit dem Seitenverhältnis:
![]() (1)
(1)
Verallgemeinerung des DIN-Rechteckes
Kreisevolvente
Spiralen
2 Beispiele
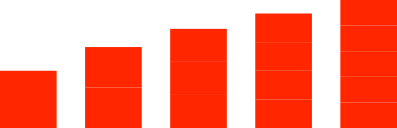
Abb. 1: Beispiele
Für n = 2 ergibt sich das klassische DIN-Format.
3 Sektoren
Die Diagonale des einen Rechteckes ist die Höhe des nachfolgenden (Abb. 2). Nachrechnen mit Pythagoras.
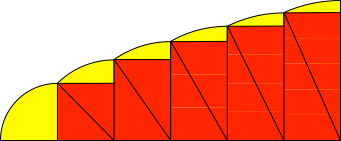
Abb. 2: Diagonalen
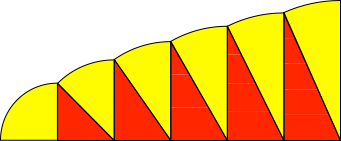
Abb. 3: Sektoren
Die Sektoren (Abb. 3) haben den Flächeninhalt Sn:
![]() (2)
(2)
Die Tabelle 1 gibt die ersten Werte. Die ersten beiden Flächeninhalte sind gleich. Anschließend haben wir ein monotones Wachstum.
|
n |
Sn |
Sn |
|
0 |
1/4*Pi |
0.7853981635 |
|
1 |
1/4*Pi |
0.7853981635 |
|
2 |
3/2*arccot(2^(1/2)) |
0.9232195632 |
|
3 |
1/3*Pi |
1.047197551 |
|
4 |
5/2*arccot(2) |
1.159119022 |
|
5 |
3*arccot(5^(1/2)) |
1.261603006 |
|
6 |
7/2*arccot(6^(1/2)) |
1.356588403 |
|
7 |
4*arccot(7^(1/2)) |
1.445468496 |
|
8 |
9/2*arccot(2*2^(1/2)) |
1.529266093 |
|
9 |
5*arccot(3) |
1.608752772 |
|
10 |
11/2*arccot(10^(1/2)) |
1.684525531 |
|
11 |
6*arccot(11^(1/2)) |
1.757056631 |
|
12 |
13/2*arccot(2*3^(1/2)) |
1.826726859 |
|
13 |
7*arccot(13^(1/2)) |
1.893848341 |
|
14 |
15/2*arccot(14^(1/2)) |
1.958680582 |
|
15 |
8*arccot(15^(1/2)) |
2.021442042 |
|
16 |
17/2*arccot(4) |
2.082318636 |
Tab. 1: Flächeninhalt der Sektoren
Die Folge {Sn} divergiert.
Für die Bogenlänge bn der Sektoren gilt:
![]() (3)
(3)
Die Tabelle 2 gibt die ersten Werte. Sie sind monoton fallend.
|
n |
bn |
bn |
|
0 |
1/2*Pi |
1.570796327 |
|
1 |
1/4*2^(1/2)*Pi |
1.110720734 |
|
2 |
3^(1/2)*arccot(2^(1/2)) |
1.066042127 |
|
3 |
1/3*Pi |
1.047197551 |
|
4 |
5^(1/2)*arccot(2) |
1.036747571 |
|
5 |
6^(1/2)*arccot(5^(1/2)) |
1.030094541 |
|
6 |
7^(1/2)*arccot(6^(1/2)) |
1.025484442 |
|
7 |
2*2^(1/2)*arccot(7^(1/2)) |
1.022100575 |
|
8 |
3*arccot(2*2^(1/2)) |
1.019510728 |
|
9 |
10^(1/2)*arccot(3) |
1.017464590 |
|
10 |
11^(1/2)*arccot(10^(1/2)) |
1.015807115 |
|
11 |
2*3^(1/2)*arccot(11^(1/2)) |
1.014437119 |
|
12 |
13^(1/2)*arccot(2*3^(1/2)) |
1.013285747 |
|
13 |
14^(1/2)*arccot(13^(1/2)) |
1.012304519 |
|
14 |
15^(1/2)*arccot(14^(1/2)) |
1.011458303 |
|
15 |
4*arccot(15^(1/2)) |
1.010721021 |
|
16 |
17^(1/2)*arccot(4) |
1.010072904 |
Tab. 2: Bogenlängen der Sektoren
Die Folge {bn} hat den Grenzwert 1.
4 Umlegen der Sektoren
Wir entfernen die noch sichtbaren halben Wurzelrechtecke (Abb. 4). Übrig bleibt die Folge der Sektoren.

Abb. 4: Folge der Sektoren
Wir denken uns die Sektoren an den gemeinsamen Punkten gelenkig verbunden und klappen zusammen (Abb. 5). Es entsteht eine aus Kreisbögen zusammengesetzte Kurve mit glatten Übergängen.
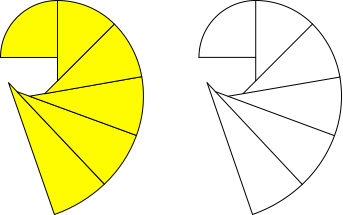
Abb. 5: Zusammenklappen
Die Abbildung 6 zeigt die ersten 101 Sektoren in zusammengeklappter Position.
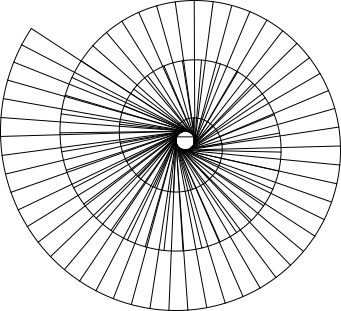
Abb. 6: 101 Sektoren
Zunächst glauben wir, eine Approximation einer archimedischen Spirale zu sehen. Andererseits sehen wir im Zentrum ein beinahe kreisrundes Loch.
Die Abbildung zeigt den durch aufeinanderfolgende Sektorenzentren gebildeten Polygonzug. Er scheint sich von innen einem Kreis mit Durchmesser 1 anzunähern.

Abb. 7: Das kreisförmige Loch
Dies kann eingesehen werden wie folgt. Die n-te Strecke des Polygonzuges hat die Länge cn:
![]() (4)
(4)
Die Richtungsänderung wn beim Übergang von der n-ten Strecke zur (n + 1)-ten Strecke beträgt:
![]() (5)
(5)
Aus (4) und (5) ergibt sich eine Richtungsänderung bezogen auf die Längenänderung:
![]() (6)
(6)
Die Tabelle 3 zeigt die ersten Werte.
|
n |
wn/cn |
|
0 |
1.570796327 |
|
1 |
1.896118900 |
|
2 |
1.936461873 |
|
3 |
1.954097237 |
|
4 |
1.964042793 |
|
5 |
1.970437895 |
|
6 |
1.974898553 |
|
7 |
1.978188124 |
|
8 |
1.980714653 |
|
9 |
1.982716256 |
|
10 |
1.984341200 |
|
11 |
1.985686699 |
|
12 |
1.986819222 |
|
13 |
1.987785552 |
|
14 |
1.988619865 |
|
15 |
1.989347438 |
|
16 |
1.989987550 |
Tab. 3: Relative Richtungsänderungen
Diese relativen Richtungsänderungen können als diskrete Krümmungen angesehen werden. Sie sind Näherungswerte für die Krümmung der approximierten Kurve. Wegen
![]() (7)
(7)
erhalten wir im Grenzfall die Krümmung 2. Eine Kurve mit der konstanten Krümmung 2 ist aber der Kreis mit dem Radius ½. Damit ist der Durchmesser 1 nachgewiesen. Ich hoffe, dass diese Argumentation stichhaltig ist.
Für den Mittelpunkt des Lochkreises erhielt ich mit einer Revolvermethode im Koordinatensystem der Abbildung 8 die Koordinaten (–0.4315, –0.1988).
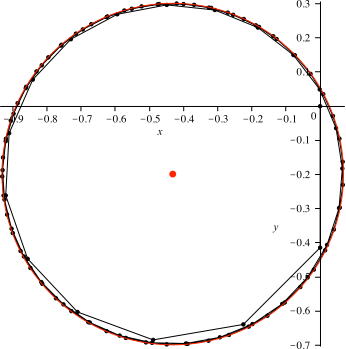
Abb. 8: Lochkreis
Daher ist es wohl sinnvoll, zu vermuten, dass die Kurve der Abbildung 6 die Kreisevolvente zum Lochkreis ist.
5 Unterteilung
Ein Hochformat-Rechteck mit dem Seitenverhältnis (1) lässt sich in n dazu kongruente Querformat-Rechtecke zerlegen. Beweis durch Nachrechnen. Die Abbildung 9 zeigt die Wurzelrechtecke für n = 1, 2, 3, 4, 5.
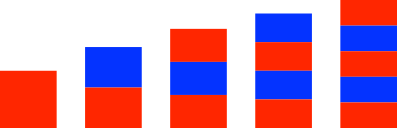
Abb. 9: Unterteilte Wurzelrechtecke
Die Abbildung 10 zeigt die ersten zehn unterteilten Wurzelrechtecke.

Abb. 10: Unterteilte Wurzelrechtecke

Abb. 11: Oberkurve und Unterkurve
Die Oberkurve (Abb. 11) ist die liegende Parabel:
![]() (8)
(8)
Die Unterkurven sind von der Form:
![]() (9)
(9)
Die Abbildung 12 zeigt die Kurven ohne die Wurzelrechtecke.
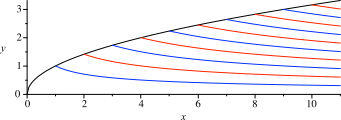
Abb. 12: Kurven
6 Eckige Wurzelspirale
Der Versuch, die Wurzelrechtecke spiralförmig anzuordnen, führt zu Überlappungen. Daher habe ich lediglich die Höhen der Rechtecke spiralförmig aneinandergefügt (Abb. 13).
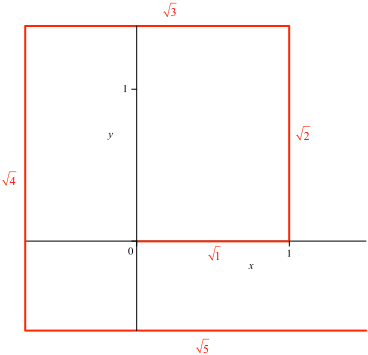
Abb. 13: Wurzelspirale
Die Abbildung 14 zeigt die ersten 100 Schritte.

Abb. 14: Wurzelspirale