Hans Walser, [20190101]

Wurzelspiralen

1 Worum geht es?

Die klassische Wurzelspurale wird etwas verändert. Dann wird es lustig.

Phänomene zum Teil ohne Beweise. Bilder und Zahlen.

2 Zur Erinnerung: die klassische Wurzelspirale

Die Abbildung 1 zeigt den Beginn der klassischen Wurzelspirale. Sie besteht aus einer Folge von rechtwinkligen Dreiecken, deren kurze Katheten (die Sehnen der Spirale) die konstante Länge 1 haben und deren lange Katheten (die Speichen der Spirale) der Reihe nach die Längen .

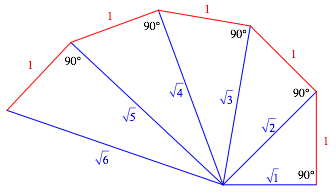
Abb. 1: Klassische Wurzelspirale

Die klassische Wurzelspirale nähert sich einer archimedischen Spirale an (Walser 2004) (Abb. 2 mit 100 Dreiecken).

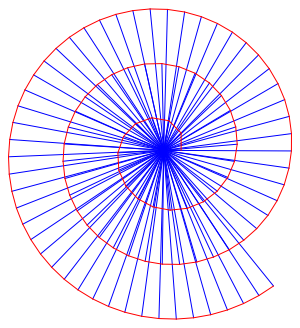
Abb. 2: Annäherung an eine archimedische Spirale

3 Modifikation

Wir ersetzen den rechten Winkel durch einen beliebigen, aber konstanten Winkel . Die Speichenlängen belassen wir auf . Das hat natürlich zur Folge, dass die Sehnenlängen nicht mehr konstant sind. Sondern interessant.

Das Problem ist uferlos. Wir beschränken uns auf den Fall .

4 Winkel 60°

4.1 Figur

Die Abbildung 1 zeigt die ersten vier Dreiecke. Die Sehnenlängen sind nicht konstant, sondern monoton wachsend. Sie bilden aber keine geometrische Folge. Die Berechnung der Sehnenlängen folgt im nächsten Abschnitt.

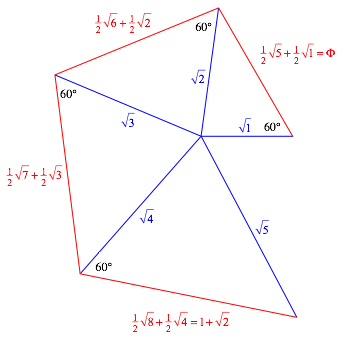
Abb. 3: Die ersten vier Dreiecke

Die Abbildung 4 zeigt das Beispiel mit den ersten 120 Dreiecken.

Abb. 4: Die ersten 120 Dreiecke

4.2 Berechnung der Sehnenlängen

Wir verwenden die Bezeichnungen der Abbildung 5.

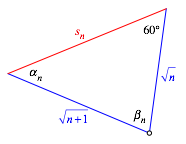
Abb. 5: Bezeichnungen

Aus dem Sinussatz folgt:

(1)

Weiter ist:

(2)

Aus dem Sinussatz folgt weiter:

(3)

Aus (1) erhalten wir:

(4)

Damit erhalten wir aus (1) und (3):

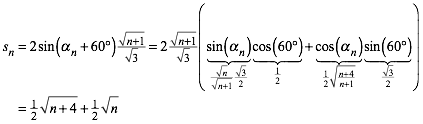(5)

Die Tabelle 1 gibt einige numerische Werte. Für negative n werden die Werte zunächst komplex und dann rein imaginär.

n	Sehnenlänge	Bemerkungen
–8	2.414213562i
–7	2.188901060i
–6	1.931851653i
–5	1.618033988i
–4	i	Imaginäre Einheit
–3	0.5 + 0.8660254040i	Argument 60°
–2	0.7071067810 + 0.7071067810i	Argument 45°
–1	0.8660254040 + 0.5i	Argument 30°
0	1	Einheit
1	1.618033988	Goldener Schnitt
2	1.931851653
3	2.188901060
4	2.414213562

Tab. 1: Numerische Werte

Die Abbildung 6 zeigt die Situation in der Gaußschen Ebene. Die Zahlen n sind rot angegeben.

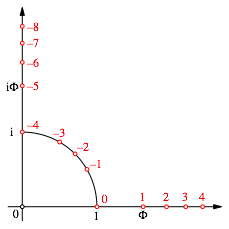
Abb. 6: In der Gaußschen Ebene

5 Der goldene Schnitt

Gemäß (5) ist:

(6)

Dies ist der goldene Schnitt (Walser 2013).

Weiter ist:

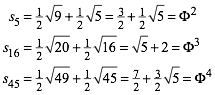(7)

Wir vermuten, dass die Folge der Potenzen des goldenen Schnittes eine Teilfolge der Sehnenfolge ist.

Ein Feldversuch lässt folgendes vermuten: Wir definieren die Folge wie folgt:

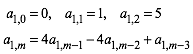(8)

Die Tabelle 2 gibt die ersten Werte.

m	1	2	3	4	5	6	7	8	9	10
	1	5	16	45	121	320	841	2205	5776	15125

Tab. 2: Erste Werte

Es handelt sich um die Folge A004146 der OEIS.

Dann ist:

(9)

6 Die zweite Sehne

Gemäß (5) ist:

(10)

Weiter ist aber:

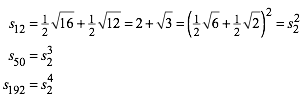(11)

Wir vermuten, dass die Folge der Potenzen von eine Teilfolge der Sehnenfolge ist. Ein Feldversuch lässt folgendes vermuten: Wir definieren die Folge wie folgt:

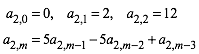(12)

Die Tabelle 3 gibt die ersten Werte.

m	1	2	3	4	5	6	7	8	9	10
	2	12	50	192	722	2700	10082	37632	140450	524172

Tab. 3: Erste Werte

Es ist dann:

(13)

Und noch ein Beispiel:

7 Die dritte Sehne

Gemäß (5) ist:

(14)

Weiter ist aber:

(15)

Wir vermuten, dass die Folge der Potenzen von eine Teilfolge der Sehnenfolge ist. Ein Feldversuch lässt folgendes vermuten: Wir definieren die Folge wie folgt:

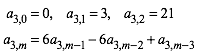(16)

Die Tabelle 4 gibt die ersten Werte.

m	1	2	3	4	5	6	7	8	9	10
	3	21	108	525	2523	12096	57963	277725	1330668	6375621

Tab. 4: Erste Werte

Es ist dann:

(17)

8 Allgemein

Allgemein geht die Sache so: Zu gegebenem n definieren wir die Folge wie folgt:

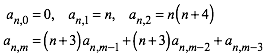(18)

Dann ist:

(19)

Die Tabelle 5 gibt den Anfang der unendlichen Matrix . Wir erkennen in den ersten Zeilen die Werte der Tabellen 1 bis 3.

1	5	16	45	121	320	841	2205	5776	15125
2	12	50	192	722	2700	10082	37632	140450	524172
3	21	108	525	2523	12096	57963	277725	1330668	6375621
4	32	196	1152	6724	39200	228484	1331712	7761796	45239072
5	45	320	2205	15125	103680	710645	4870845	33385280	228826125
6	60	486	3840	30246	238140	1874886	14760960	116212806	914941500
7	77	700	6237	55447	492800	4379767	38925117	345946300	3074591597
8	96	968	9600	95048	940896	9313928	92198400	912670088	9034502496
9	117	1296	14157	154449	1684800	18378369	200477277	2186871696	23855111397
10	140	1690	20160	240250	2862860	34114090	406506240	4843960810	57721023500

Tab. 5: Matrix

9 Quadratzahlen

Wir dividieren in der Tabelle 4 die Einträge in den Spalten mit ungeraden Spaltennummern durch die entsprechenden Einträge der ersten Spalte und die Einträge in den Spalten mit geraden Spaltennummern durch die Einträge in der zweiten Spalte (Tab. 6).

1	1	16	9	121	64	841	441	5776	3025
1	1	25	16	361	225	5041	3136	70225	43681
1	1	36	25	841	576	19321	13225	443556	303601
1	1	49	36	1681	1225	57121	41616	1940449	1413721
1	1	64	49	3025	2304	142129	108241	6677056	5085025
1	1	81	64	5041	3969	312481	246016	19368801	15249025
1	1	100	81	7921	6400	625681	505521	49420900	39929761
1	1	121	100	11881	9801	1164241	960400	114083761	94109401
1	1	144	121	17161	14400	2042041	1713481	242985744	203889841
1	1	169	144	24025	20449	3411409	2903616	484396081	412293025

Tab. 6: Quotienten

Wir erhalten ausschließlich Quadratzahlen. Die Tabelle 7 gibt die zugehörigen Wurzeln.

1	1	4	3	11	8	29	21	76	55
1	1	5	4	19	15	71	56	265	209
1	1	6	5	29	24	139	115	666	551
1	1	7	6	41	35	239	204	1393	1189
1	1	8	7	55	48	377	329	2584	2255
1	1	9	8	71	63	559	496	4401	3905
1	1	10	9	89	80	791	711	7030	6319
1	1	11	10	109	99	1079	980	10681	9701
1	1	12	11	131	120	1429	1309	15588	14279
1	1	13	12	155	143	1847	1704	22009	20305

Tab. 7: Wurzeln

Die in der ersten Zeile gelb unterlegten Zahlen 1, 4, 11, 29, 76, ... sind eine Auswahl aus den Lucas-Zahlen 1, 3, 4, 7, 11, 18, 29, 47, 76, ... . Die blau unterlegten Zahlen 1, 3, 8, 21, 55, ... sind eine Auswahl aus den Fibonacci-Zahlen. Die mit gleicher Farbe unterlegten Zahlen haben je die Rekursion:

(20)

In der zweiten Zeile haben die mit gleicher Farbe unterlegten Zahlen je die Rekursion:

(21)

Und so weiter.

Weiter ist jede gelbe Zahl die Summe der beiden links und rechts benachbarten blauen Zahlen.

In der ersten Zeile ist jede blaue Zahl ein Fünftel der Summe der beiden benachbarten gelben Zahlen. In der zweiten Zeile ist jede blaue Zahl ein Sechstel der Summe der beiden benachbarten gelben Zahlen. In der dritten Zeile ist jede blaue Zahl ein Siebtel der Summe der beiden benachbarten gelben Zahlen. Und so weiter.

Literatur

Walser, Hans (2004): Pythagoras, eine archimedische Spirale und eine Approximation von π. Praxis der Mathematik (6/46), 2004, S. 287-288.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.

Websites

OEIS

https://oeis.org/A004146