Hans Walser, [20130505]
Yin Yang
Eine nostalgische fraktale Erinnerung. Anregung: Strick (2013)
1 Yin Yang Figur
Die Abbildung 1 zeigt das Yin Yang, wie es leibt und lebt.

Abb. 1: Yin Yang
Es ist unter Farbwechsel punktsymmetrisch. Weiter hat es keine Symmetrien.
1.1 Reduktion auf 50%
1.1.1 Fraktal
Nun zeichnen wir zwei halb so gro§e Kopien und passen sie ein (Abb. 2).

Abb. 2: Einpassen von Kopien
Diesen Prozess wiederholen wir. Die Abbildung 3 zeigt den nŠchsten Schritt.

Abb. 3: NŠchster Schritt
Die Figur ist immer noch unter Farbwechsel punktsymmetrisch. Die Trennlinie in der Mitte ist gleich lang wie der halbe Kreisumfang.
Nach unendlich vielen Schritte (um ehrlich zu sein: nach 7 Schritten) ergibt sich die Figur der Abbildung 4.

Abb. 4: Unendlich viele Schritte
Die Figur ist immer noch unter Farbwechsel punktsymmetrisch. Und die Trennlinie gleich lang wie der halbe Umfang. ăVon AugeŇ allerdings sieht man eine Achsensymmetrie mit horizontaler Achse und eine Achsensymmetrie mit vertikaler Achse unter Farbwechsel sowie einen Durchmesser als Trennlinie. Also zwei Halbkreise. Das Charisma von Yin Yang fehlt.
1.1.2 Drehung um 180ˇ
Spannender wird es, wenn wir die Teilfiguren zusŠtzlich um 180ˇ drehen. Die Abbildung 5 zeigt den ersten Schritt. Die Figur ist punktsymmetrisch unter Farbwechsel.

Abb. 5: Drehung um 180ˇ
Nun fahren wir so weiter. Die Abbildung 6 zeigt den nŠchsten Schritt.

Abb. 6: NŠchster Schritt
Die Abbildung 7 zeigt, was sich nach unendlich vielen (also sieben) Schritten ergibt. Wir haben ein so genanntes Fraktal.

Abb. 7: Nach sieben Schritten
Die Figur ist immer noch punktsymmetrisch unter Farbwechsel, aber das naive Auge sieht auch eine Achsensymmetrie mit horizontaler Achse sowie eine Achsensymmetrie mit vertikaler Achse unter Farbwechsel.
Das Šndert sich, wenn wir noch Drehungen einbauen.
1.1.3 Drehung um —90ˇ
Wir drehen die Teilfiguren um –90ˇ, also um 90ˇ im Uhrzeigersinn (Abb. 8 und 9).

Abb. 8: Drehung um 90ˇ im Uhrzeigersinn

Abb. 9: Drehung um 90ˇ im Uhrzeigersinn. Fraktal
Die Punktsymmetrie unter Farbwechsel ist offensichtlich. Achsensymmetrien hat es keine mehr.
1.2 Reduktion auf 40%
1.2.1 Fraktal
Beim Verfahren der Abbildungen 2, 3 und 4 ist das Charisma von Yin Yang weg. Das kann gerettet werden, indem wir nicht auf die HŠlfte, sondern zum Beispiel auf 40% reduzieren (Abb. 10 und 11).

Abb. 10: Reduktion auf 40%

Abb. 11: Fraktal mit Reduktion 40%
1.2.2 Zusatzspiegelung
Wir kšnnen noch Zusatzoperationen einbauen, zum Beispiel eine Spiegelung an der von links unten nach rechts oben laufenden SchrŠgen (Abb. 12 und 13).

Abb. 12: Spiegelung

Abb. 13: Fraktal mit Reduktion 40% und Spiegelung
2 Eckige Yin Yang Figur
2.1 Hexagonalbasis
Wir kšnnen die Kreise durch regelmŠ§ige Vielecke mit gerader Eckenzahl ersetzen. Die Abbildung 14 zeigt das Yin Yang auf der Basis des Hexagons.
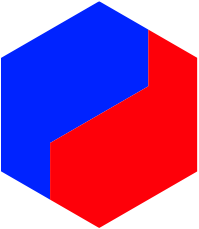
Abb. 14: Hexagonales Yin Yang
2.1.1 Reduktion auf 50%
Wir kšnnen nun zum Beispiel auf 50% reduzieren und dem Hexagon angepasst um 60ˇ drehen (Abb. 15 und 16).

Abb. 15: Reduktion 50%, Drehung 60ˇ

Abb. 16: Reduktion 50%, Drehung 60ˇ. Fraktal
2.1.2 Reduktion auf 40%
Im Beispiel der Abbildung 17 ist auf 40% reduziert und um 60ˇ gedreht.

Abb. 17: Reduktion 40%, Drehung 60ˇ. Fraktal
2.2 Quadratische Basis
Das einfachste regelmŠ§ige Vieleck mit gerader Eckenzahl ist das Quadrat. Das zugehšrige Yin Yang ist allerdings kaum erkennbar (Abb. 18).

Abb. 18: Quadratisches Yin Yang
2.2.1 Reduktion auf 50%
Im Beispiel der Abbildung 19 ist auf 50% reduziert und um 180ˇ gedreht.

Abb. 19: Reduktion 50%, Drehung 180ˇ
2.2.2 Reduktion auf 40%
Im Beispiel der Abbildung 20 ist auf 40% reduziert und um 180ˇ gedreht.

Abb. 20: Reduktion 40%, Drehung 180ˇ
3 Fraktale Dimensionen
Die Yin Yang Fraktale mit dem Reduktionsfaktor 50% haben die fraktale Dimension 1 (Mandelbrot 1983), (Mandelbrot 1991).
Die Yin Yang Fraktale mit dem Reduktionsfaktor 40% haben die fraktale Dimension:
![]()
Literatur
Mandelbrot, Beno”t B. (1983). The Fractal Geometry of Nature. New York: Freeman. ISBN 0-7167-1186-9
Mandelbrot, Beno”t B. (1991). Die fraktale Geometrie der Natur. Basel: BirkhŠuser.
Strick, Heinz Klaus (2013). Yin und Yang. MNU, Der mathematische und naturwissenschaftliche Unterricht, 66(3), 189, ISSN 0025-5866, © Verlag Klaus Seeberger, Neuss