Hans Walser, [20200925]
Zahlendreieck
1 Worum geht es?
Zahlenspielerei im Kontext der Division durch 9 im Dezimalsystem
2 Das Zahlendreieck
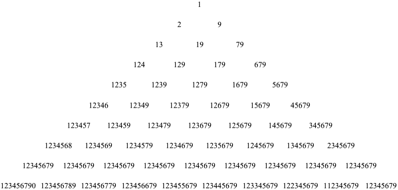
Abb. 1: Das Zahlendreieck
Im Anhang ist das Zahlendreieck vergrš§ert dargestellt.
Die Abbildung 2 zeigt einen kleineren Ausschnitt.

Abb. 2: Kleinerer Ausschnitt
3 Zeilensummen
Die Tabelle 1 gibt die Zeilensummen und die alternierenden Zeilensummen.
|
n |
Zeilensummen |
Alternierende Zeilensummen |
|
1 |
1 |
1 |
|
2 |
11 |
–7 |
|
3 |
111 |
73 |
|
4 |
1111 |
–505 |
|
5 |
11111 |
5275 |
|
6 |
111111 |
–30303 |
|
7 |
1111111 |
325477 |
|
8 |
11111111 |
–1010101 |
|
9 |
111111111 |
12345679 |
|
10 |
1111111111 |
101010101 |
|
11 |
11111111111 |
–785634119 |
|
12 |
111111111111 |
30303030303 |
|
13 |
1111111111111 |
–280583613917 |
|
14 |
11111111111111 |
5050505050505 |
|
15 |
111111111111111 |
–48260381593715 |
|
16 |
1111111111111111 |
707070707070707 |
|
17 |
11111111111111111 |
–6846240179573513 |
|
18 |
111111111111111111 |
90909090909090909 |
|
19 |
1111111111111111111 |
–886644219977553311 |
|
20 |
11111111111111111111 |
11111111111111111111 |
|
21 |
111111111111111111111 |
–108866442199775533109 |
|
22 |
1111111111111111111111 |
1313131313131313131313 |
|
23 |
11111111111111111111111 |
–12906846240179573512907 |
|
24 |
111111111111111111111111 |
151515151515151515151515 |
|
25 |
1111111111111111111111111 |
–1492704826038159371492705 |
|
26 |
11111111111111111111111111 |
17171717171717171717171717 |
|
27 |
111111111111111111111111111 |
–169472502805836139169472503 |
|
28 |
1111111111111111111111111111 |
1919191919191919191919191919 |
|
29 |
11111111111111111111111111111 |
–18967452300785634118967452301 |
|
30 |
111111111111111111111111111111 |
212121212121212121212121212121 |
Tab. 1: Zeilensummen
Der gelb unterlegte Teil entspricht dem Ausschnitt der Abbildung 1.
4 Hintergrund
Das Zahlendreieck wurde konstruiert wie folgt:
9 : 9 = 1
18 : 9 = 2 81 : 9 = 9
117 : 9 = 13 171 : 9 = 19 711 : 9 = 79
1116 : 9 = 124 1161 : 9 = 129 1611 : 9 = 179 6111 : 9 = 679
Der Divisor ist immer 9. Der Dividend besteht aus Einsen und einer weiteren Zahl, welche die Quersumme auf 9 ergŠnzt.
Die Berechnung geschieht so:
for n from 1 to N do
for k from 1 to n do
a[n,k] := (sum(10^j, j = 0..n-1) + (9 - n)*10^(k-1))/9:
end:
end:
In bźrgerlicher Schreibweise:
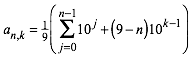 (1)
(1)
Anhang
