Hans Walser, [20091017a]
Zahlendreieck beim Tangens
Was geschieht, wenn wir die Tangensfunktion mehrfach ableiten?
Bearbeitung
Wir verwenden die
Ableitungsformel:
Damit erhalten wir:
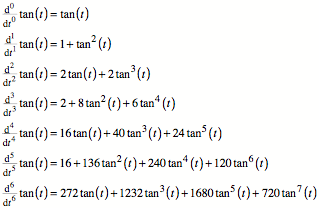
Aus Systemgrźnden wurde
oben noch die nullte Ableitung, also die Funktion selber, eingefźgt.
Wir interessieren uns
um das Koeffizientendreieck. Es sei 
der Koeffizient
von 
in der i-ten Ableitung 
. Fźr diese Koeffizienten erhalten wir die Tabelle:
|
i \ j |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
|
1 |
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
3 |
2 |
|
8 |
|
6 |
|
|
|
|
4 |
|
16 |
|
40 |
|
24 |
|
|
|
5 |
16 |
|
136 |
|
240 |
|
120 |
|
|
6 |
|
272 |
|
1232 |
|
1680 |
|
720 |
In der letzten
SchrŠgzeile erkennen wir die FakultŠten.
Mit den Startwerten 
, 
und 
gilt die
Rekursion:
Dies wird aus dem
Ableitprozedere induktiv ersichtlich.
Die Zahlen wachsen sehr
rasch.
|
i\j |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
2 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
2 |
0 |
8 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
16 |
0 |
40 |
0 |
24 |
0 |
0 |
0 |
0 |
|
5 |
0 |
16 |
0 |
136 |
0 |
240 |
0 |
120 |
0 |
0 |
0 |
|
6 |
0 |
0 |
272 |
0 |
1232 |
0 |
1680 |
0 |
720 |
0 |
0 |
|
7 |
0 |
272 |
0 |
3968 |
0 |
12096 |
0 |
13440 |
0 |
5040 |
0 |
|
8 |
0 |
0 |
7936 |
0 |
56320 |
0 |
129024 |
0 |
120960 |
0 |
40320 |