1 Worum geht es?

Es wird eine falsche Methode zur Bestimmung der Kreiszahl π diskutiert.

2 Konstruktion der Zahnräder

Auf dem Einheitskreis wählen wir 6 gleichmäßig verteilte Punkte und errichten über je zwei benachbarten Punkten ein gleichschenkliges Dreieck der Kantenlänge 1 (Abb. 1a). So entsteht das erste Zahnrad. Es hat den Umfang 12. Die konvexe Hülle des Zahnrades ist grün eingezeichnet.

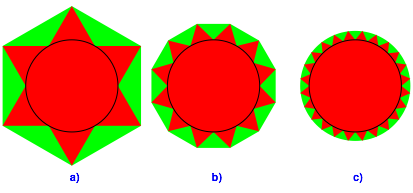
Abb. 1: Die ersten drei Zahnräder

Nun modifizieren wir das Zahnrad, indem wir die Anzahl der Zähne verdoppeln, dafür die Kantenlänge der Zähne halbieren (Abb. 1b). Man beachte, dass die aufgesetzten Dreiecke nun nicht mehr gleichseitig sind, sondern nur noch gleichschenklig mit der Schenkellänge . Die Basislänge ist:

(1)

Der Winkel an der Außenspitze misst:

(2)

Das neue Zahnrad hat immer noch den Umfang 12. Die Abbildung 1c zeigt den nächsten entsprechenden Modifikationsschritt.

Die Abbildung 2 zeigt die ersten zehn Zahnräder. Die Zähne werden zahlreicher und kleiner. Bald einmal ist das Zahnrad nicht mehr vom Kreis unterscheidbar.

Abb. 2: Die ersten zehn Zahnräder

3 Die Daten

Die Tabelle 1 enthält für jedes Zahnrad den Flächeninhalt, den Umfang, den Flächeninhalt der konvexen Hülle und den Umfang der konvexen Hülle.

N	Flächeninhalt Zahnrad	Umfang Zahnrad	Flächeninhalt konvexe Hülle	Umfang konvexe Hülle
1	5.19615	12	7.79423	10.3923
2	4.32867	12	5.82741	8.65735
3	3.77377	12	4.50724	7.54754
4	3.46705	12	3.82075	6.93409
5	3.30661	12	3.47906	6.61323
6	3.22467	12	3.30965	6.44934
7	3.18327	12	3.22543	6.36655
8	3.16247	12	3.18346	6.32494
9	3.15204	12	3.16252	6.30408
10	3.14682	12	3.15205	6.29364
Grenzwert	π	12	π	2π

Tab. 1: Fläche und Umfang

Mit wachsender Modifikationszahl N nähern sich die Zahnräder dem Einheitskreis an. Der Flächeninhalt und die Daten der konvexen Hülle spielen mit. Der Umfang der Zahnräder spielt nicht mit. Es ist daher falsch, mit dieser Methode die Kreiszahl π zu bestimmen. Es käme π = 6 heraus, fast das Doppelte des richtigen Wertes.

Eine weitere neckische Eigenschaft der Tabelle 1 besteht darin, dass die Maßzahl des Umfanges der konvexen Hülle für jedes N genau das Doppelte der Maßzahl des Flächeninhaltes des zugehörigen Zahnrades zu sein scheint. Der Autor hat keinen Beweis dafür.

4 Diskussion des Umfangfehlers

Zwar nähern sich alle Randpunkte des Zahnrades dem Einheitskreis. Hingegen nähern sich die Richtungen der Zahnkanten nicht der jeweiligen Tangentenrichtung des Einheitskreises. Es wird daher schräg gemessen. Dies ist ein alter Trick (ein Didaktiker würde sagen „eine fundamentale Kernkonzept-Idee“) um Leute hinters Licht zu führen.

5 Es kommt noch besser (oder schlechter)

Wir beginnen wieder mit dem Zahnrad mit den sechs Zähnen (Abb. 1a und 3a).

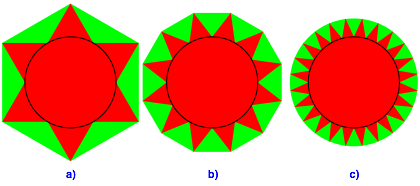
Abb. 3: Es wird zackiger

Wir verdoppeln nun wieder die Anzahl der Zähne, reduzieren die Kantenlänge der Zähne aber nur auf (Abb. 3b). Dadurch wird der Umfang mit dem Faktor erhöht. Die Abbildung 3c zeigt den dritten Fall.

Die Abbildung 4 zeigt die ersten zehn Zahnräder.

Abb. 4: Die ersten zehn zackigen Zahnräder

Die Zahnräder nähern sich wiederum dem Einheitskreis an.

Die Tabelle 2 gibt die entsprechenden Daten.

N	Flächeninhalt Zahnrad	Umfang Zahnrad	Flächeninhalt konvexe Hülle	Umfang konvexe Hülle
1	5.19615	12	7.79423	10.3923
2	4.90814	16	7.49206	9.81629
3	4.43671	21.33333	6.22992	8.87342
4	4.03986	28.44444	5.18755	8.07972
5	3.75123	37.92593	4.47757	7.50246
6	3.55152	50.5679	4.01457	7.10303
7	3.41605	67.42387	3.71441	6.83211
8	3.32498	89.89849	3.51905	6.64996
9	3.264	119.86465	3.39116	6.52799
10	3.22325	159.81954	3.30702	6.44649
Grenzwert	π	divergent	π	2π

Tab. 2: Fläche und Umfang

Wiederum schert der Umfang des Zahnrades aus. Er ist eine geometrische Folge mit dem Wachstumsfaktor und divergiert.

Wir haben also die Situation, dass eine flächenmäßig beschränkte Figur einen beliebig großen Umfang haben kann. Dies erinnert an die Fraktale, etwa die Schneeflocke von Helge von Koch.

Erneut scheint die Maßzahl des Umfanges der konvexen Hülle das Doppelte der Maßzahl des Flächeninhaltes des Zahnrades zu sein.