Hans Walser, [20210219]
ZahnrŠder
1 Worum geht es?
Ein kinematisches Beispiel mit zwšlf ZahnrŠdern.
2 Die zwšlf ZahnrŠder
Die kleinen ZahnrŠder (Abb. 1) haben 19 ZŠhne, die gro§en 57. Die roten ZahnrŠder drehen im positiven Drehsinn, die blauen im negativen. Jedes rote Zahnrad ist mit drei blauen verzahnt und umgekehrt.
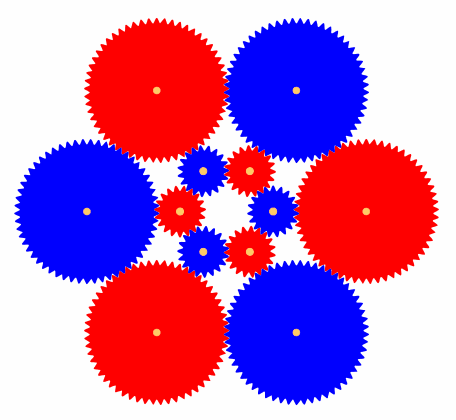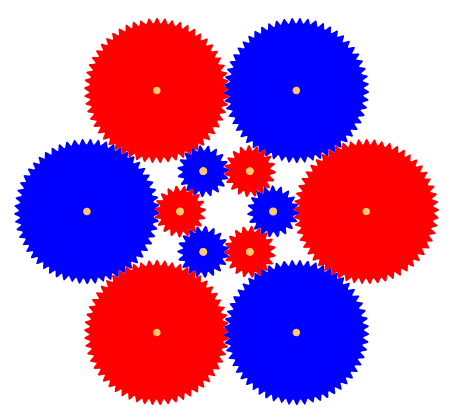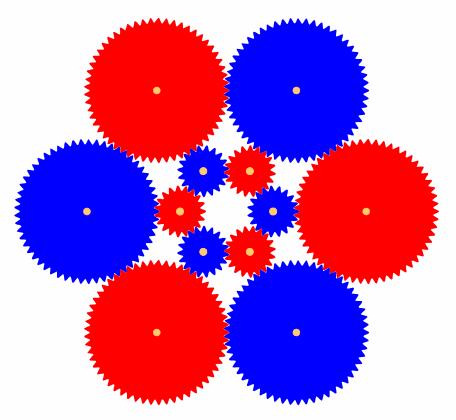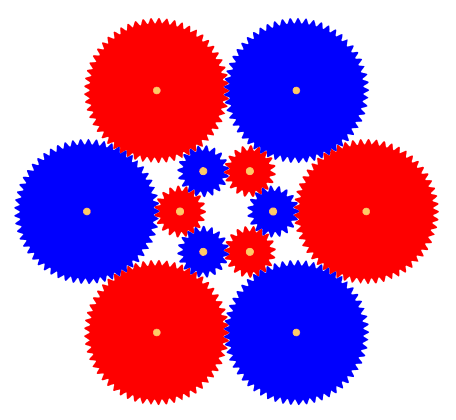
Abb. 1: Die zwšlf ZahnrŠder
Die ZŠhne der ZahnrŠder sind durch Sinuskurven in Polardarstellung modelliert. Sie sind also nur eine Approximation an die Evolventen, aus denen die ZŠhne lege artis gemacht werden mźssten. Die technische Folge ist, dass die ZŠhne sich teilweise źberlappen. Das ist in den Abbildungen kaum sichtbar.
Wir variieren nun die Anzahlen der ZŠhne.
3 Zahnlos
Da haben wir nur RŠder, die aufeinander abrollen (Abb. 2). Um das Drehen der RŠder sichtbar zu machen, sind Speichen eingezeichnet.
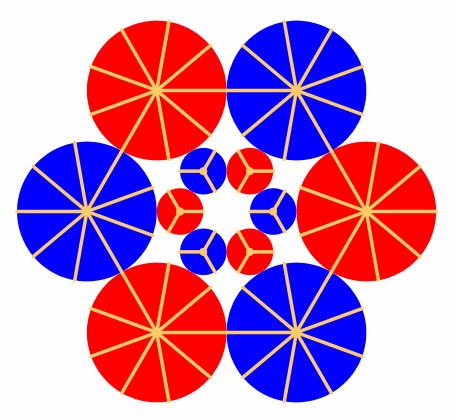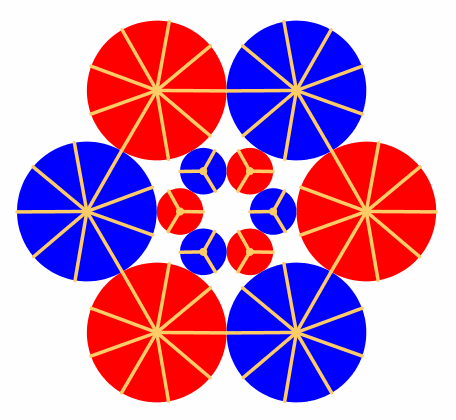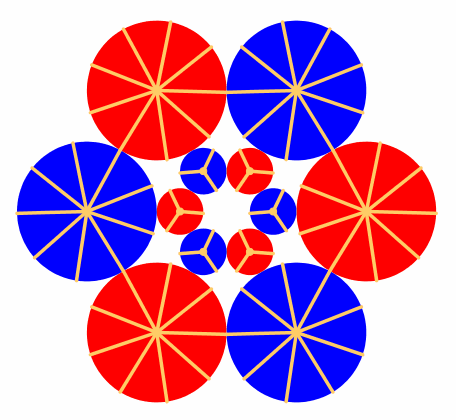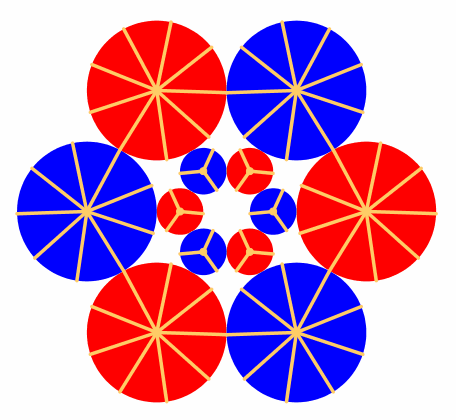
Abb. 2: Abrollen von zahnlosen RŠdern
4 Ein Zahn
Wegen der Modellierung der ZŠhne mit Sinuskurven sieht es bei einem Zahn (fźr das kleine Zahnrad) ganz sanft aus (Abb. 3).
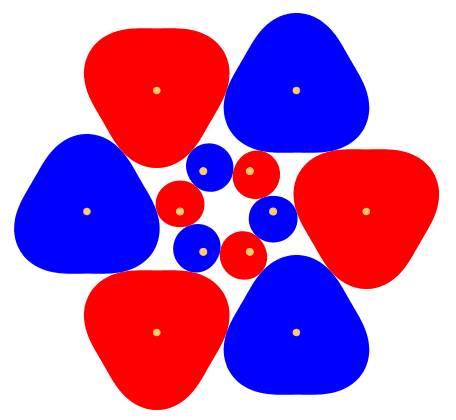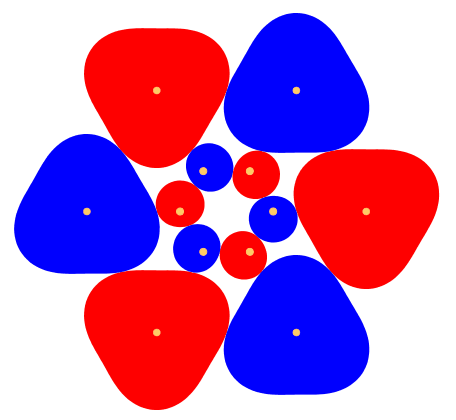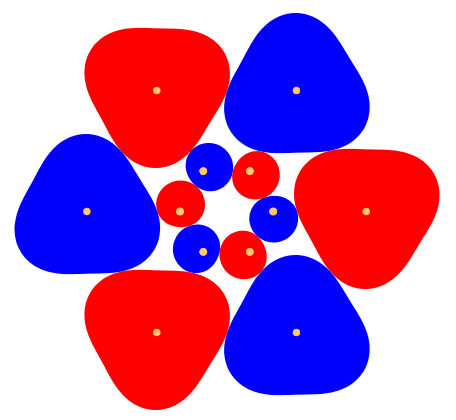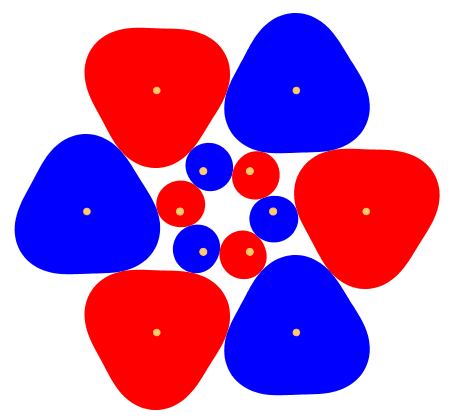
Abb. 3: Ein Zahn
Wird die Amplitude der Sinuskurve gleich dem TrŠgerkreisradius gewŠhlt, ergeben sich Kardioiden fźr die kleinen ZahnrŠder (Abb. 4). Die krass fehlende KonvexitŠt fźhrt zu †berschneidungen. Sogar gleichsinnig drehende RŠder kšnnen sich źberschneiden.
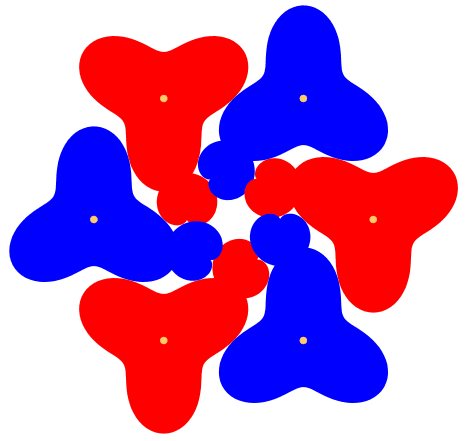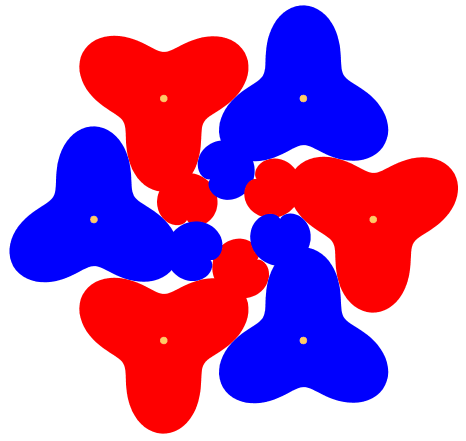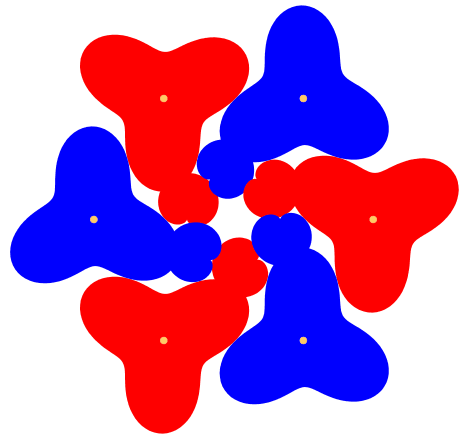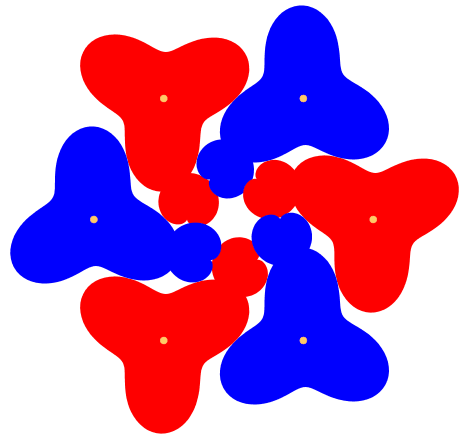
Abb. 4: Kardioiden
5 Zwei und mehr ZŠhne
Die Abbildung 5 zeigt ein Beispiel mit zwei ZŠhnen fźr die kleinen ZahnrŠder.
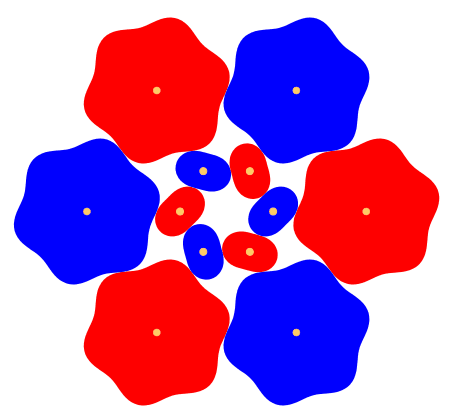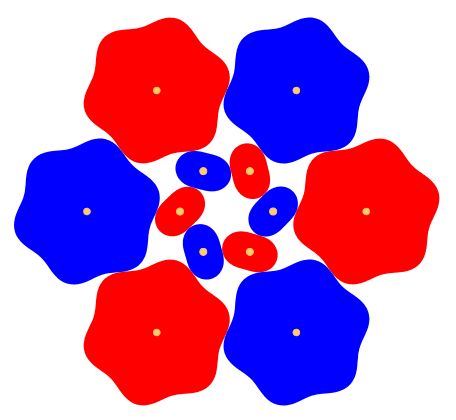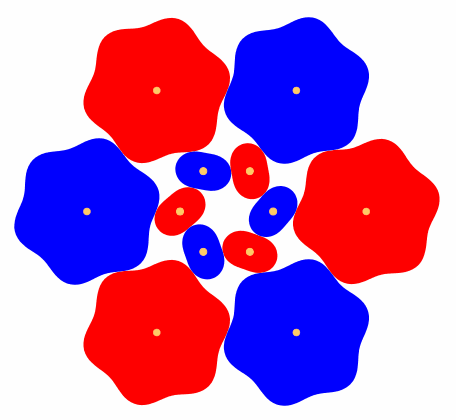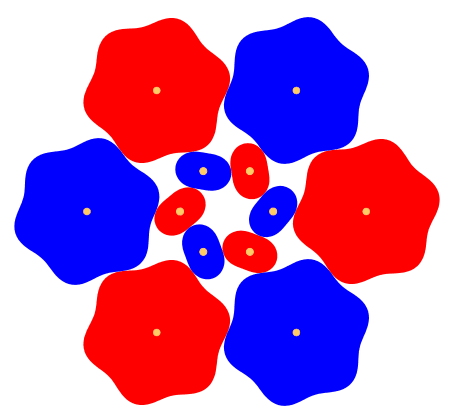
Abb. 5: Zwei ZŠhne
Wird die Amplitude der Sinuskurve gleich dem TrŠgerkreisradius gewŠhlt, ergeben sich Propeller fźr die kleinen ZahnrŠder (Abb. 6). Die fehlende KonvexitŠt fźhrt zu †berschneidungen. Sogar gleichsinnig drehende RŠder kšnnen sich źberschneiden.

Abb. 6: Propeller
Die folgenden Abbildungen zeigen weitere Beispiele. Interessant ist, dass Beispiele mit fźnf (Abb. 9) oder sieben (Abb. 11) ZahnrŠdern durchaus mšglich sind, obwohl die Gesamtfigur eine Sechserteilung hat.
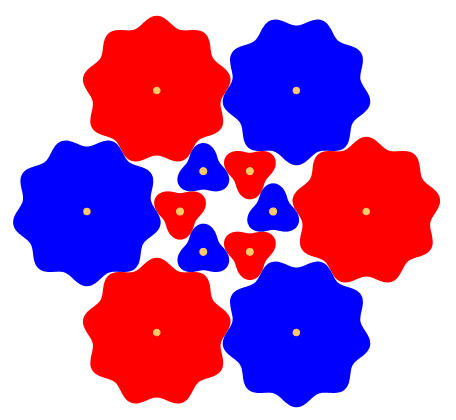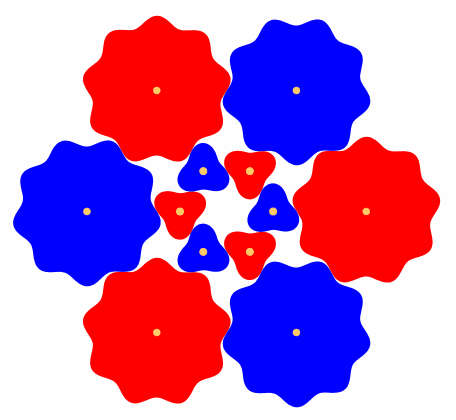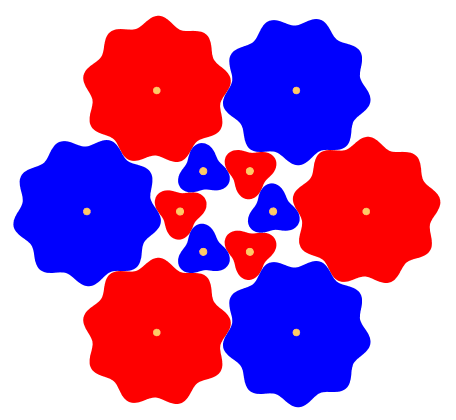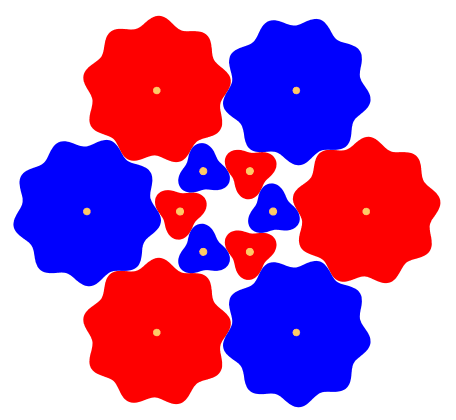
Abb. 7: Drei ZŠhne
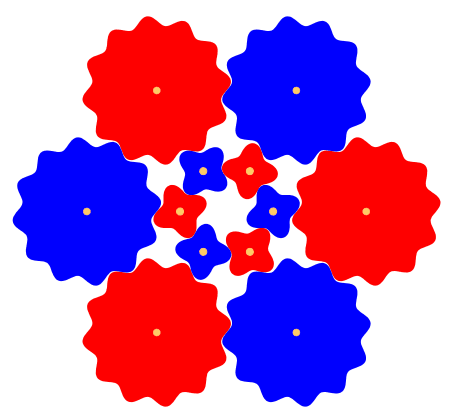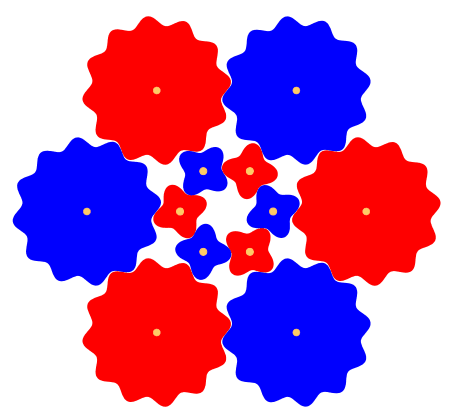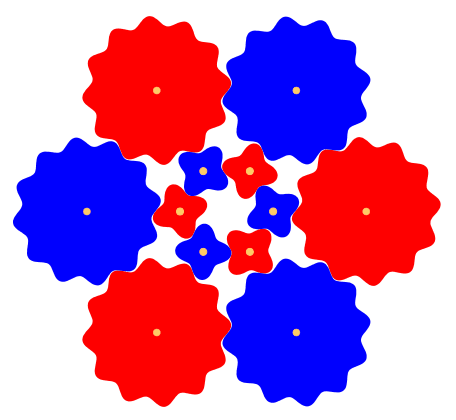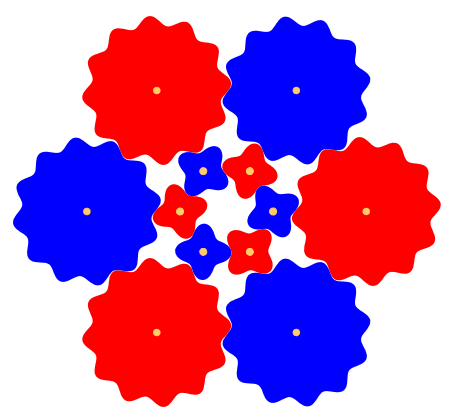
Abb. 8: Vier ZŠhne

Abb. 9: Fźnf ZŠhne

Abb. 10: Sechs ZŠhne

Abb. 11: Sieben ZŠhne
6 Viererteilung
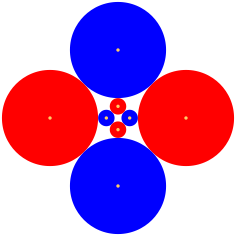
Abb. 12: Viererteilung
Die Situation der Abbildung 12 lŠsst sich nicht zu einem Zahnradgetriebe verwenden. Die Radien und damit auch die UmfŠnge der gro§en und der kleinen Kreise stehen in einem irrationalen VerhŠltnis, was eine Zahnung ausschlie§t.
Der Autor vermutet, dass die Sechserteilung (Abb. 1 bis 11) einen singulŠren Fall darstellt.
Websites
Hans
Walser: ZahnrŠder
http://www.walser-h-m.ch/hans/Miniaturen/Z/Zahnraeder2/Zahnraeder2.htm
Hans Walser: ZahnrŠder
http://www.walser-h-m.ch/hans/Miniaturen/Z/Zahnraeder/Zahnraeder.htm