Hans Walser, [20130422]

Die Zaunaufgabe

1 Die Uraltaufgabe

Die Uraltaufgabe besteht darin, an eine Mauer einen rechteckigen Hühnerpferch der Gesamtlänge a zu bauen (Abb. 1). Vgl. [Vogel / Wittmann 2010].

Abb. 1: Aufgabenstellung

Nun soll der Flächeninhalt des Rechteckes maximiert werden.

1.1 Rechnerische Lösung

Die Rechnung geht so:

(1)

Für den Flächeninhalt A ergibt sich:

(2)

Maximum:

(3)

Damit erhalten wir und . Die Abbildung 2 zeigt das optimale Rechteck.

Abb. 2: Optimales Rechteck

Die optimale Lösung ist ein halbes Quadrat der Seitenlänge (Abb. 3).

Abb. 3: Halbes Quadrat

1.2 Lösung mit dynamischer Geometrie

Wir gehen aus von einem Pferch mit stimmiger Gesamtlänge (Abb. 1) und zeichnen symmetrisch zwei blaue Linien in V-Form mit Steigungswinkeln 45° ein (Abb. 4) sowie dazu zwei orthogonale magenta Linien durch die Eckpunkte des Pferches.

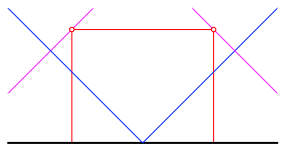
Abb. 4: Vorbereitung

Nun verschieben wir die beiden Ecken des Pferches gegen die blauen Linien (Abb. 5). Was die Länge des Zaunes betrifft, so kompensieren sich die Gewinne und Verluste. Anders bei den Flächeninhalten: Zunächst ergeben sich ein gelber Flächenverlust und zwei grüne Flächengewinne.

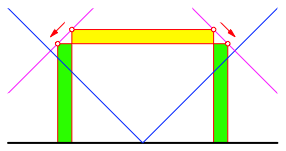
Abb. 5: Verluste und Gewinne

Wenn wir die Sache nach unten spiegeln, sehen wir, dass per Saldo die Gewinne größer sind (Abb. 6).

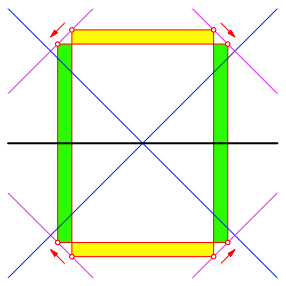
Abb. 6: Mehr Gewinne als Verluste

Statt mit Verdoppeln können wir eben so gut mit Halbieren arbeiten (Abb. 7).

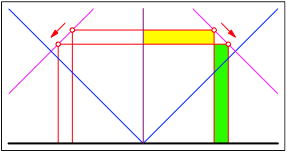
Abb. 7: Halbieren

Die Abbildung 8 zeigt die Situation (mit Verdoppeln), wenn wir mit einem sehr niedrigen Pferch beginnen.

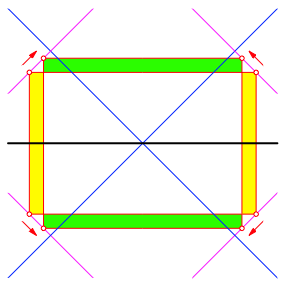
Abb. 7: Querformat

Mit einem Verschieben der Ecken in Richtung der blauen Geraden gibt es jedenfalls eine Flächenvergrößerung. Die optimale Lösung ergibt sich also, wenn die Ecken sich auf den blauen Linien befinden. Dann haben wir aber ein Quadrat und als Hühnerpferch ein halbes Quadrat. Wir können dann nicht mehr verbessern.

2 Schräger Hühnerpferch

Der Zaun soll nun schräg von der Mauer ausgehen, ansonsten aber rechte Winkel aufweisen (Abb. 9).

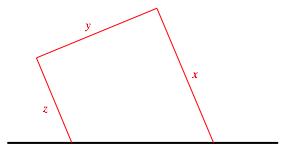
Abb. 9: Schräger Hühnerpferch

Wir haben neu eine dritte Variable, nämlich z. Es gilt wegen der gegebenen Zaunlänge a:

(4)

Somit ist:

(5)

Der zu optimierende Flächeninhalt A ist nun eine Trapezfläche.

(6)

Wegen (5) gilt:

(7)

Dies ist die Funktion (2) vom Rechteckbeispiel. Wir erhalten für die optimale Lösung den y-Wert . Dieser Wert ist unabhängig von der Schräglage des Hühnerpferches. Von den beiden übrigen Variablen x und z können wir eine frei wählen, zum Beispiel x. Dann ist .

Die Abbildung 10 zeigt eine mögliche optimale schräge Lösung.

Abb. 10: Eine optimale schräge Lösung

Auch diese Lösung ist ein halbes Quadrat (Abb. 11).

Abb. 11: Halbes Quadrat

Natürlich kann auch im schrägstehenden Fall mit dynamischer Geometrie gearbeitet werden (Abb. 12).

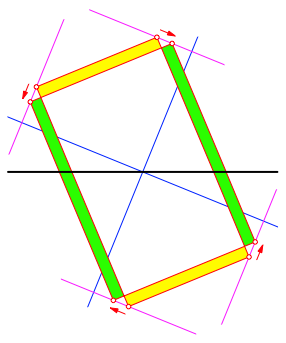
Abb. 12: Lösung mit Beweglichkeit

Die von uns auf dem rechnerischen Weg frei gewählte Variable x hängt mit der Schrägstellung des Quadrates zusammen. Für den in der Abbildung 13 eingezeichneten Winkel gilt:

(8)

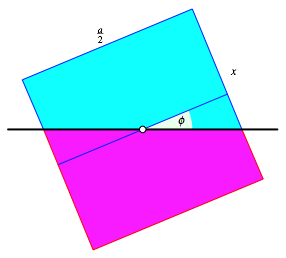
Abb. 13: Schrägstellung

Für ergibt sich der Sonderfall der Abbildung 14.

Abb. 14: Sonderfall

Literatur

[Vogel / Wittmann 2010] Vogel, Markus und Wittmann, Gerald: Mit Darstellungen arbeiten – tragfähige Vorstellungen entwickeln. PM, Praxis der Mathematik in der Schule Sekundarstufen 1 und 2, Heft 32, April 2010, 52. Jg., S. 1-8.