Hans Walser, [20130516], [20130520], [20130525b]

Zerlegungsgleichheit

1 Worum es geht

In der Ebene sind flächengleiche Polygone immer auch zerlegungsgleich.

Wie finden wir bei Dreiecken und Rechtecken eine gemeinsame Zerlegung?

2 Dreiecke

2.1 Gleiche Grundlinie und gleiche Höhe

Zwei Dreiecke mit gleicher Grundlinie und gleicher Höhe sind flächengleich. Die Abbildung 1 zeigt das Vorgehen zur Auffindung der Zerlegungsgleichheit. Dabei werden 5 Puzzle-Teile verwendet. Wir arbeiten mit einem Vergleichsrechteck.

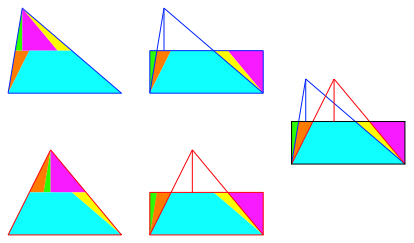
Abb. 1: Gleiche Grundlinie und Höhe

Es geht auch mit nur vier Puzzle-Teilen (Abb. 2). Wir arbeiten mit einem Vergleichsparallelogramm, das sich am oberen Dreieck orientiert.

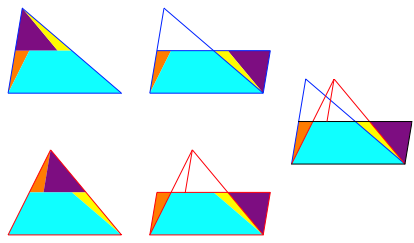
Abb. 2: Nur vier Puzzle-Teile

Die Abbildung 3 zeigt einen Fall mit „hohen“ Dreiecken.

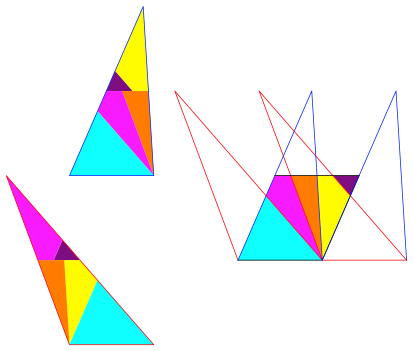
Abb. 3: „Hohe“ Dreiecke

Die Abbildung 4 zeigt ein noch höheres Beispiel mit 15 Puzzle-Teilen. Das Vergleichsparallelogramm ist zweimal gezeichnet.

Abb. 4: Sehr hohe Dreiecke

2.2 Ein gemeinsamer Winkel

Wir gehen von zwei flächengleichen Dreiecken aus, welche zudem einen Winkel gemeinsam haben (Abb. 5).

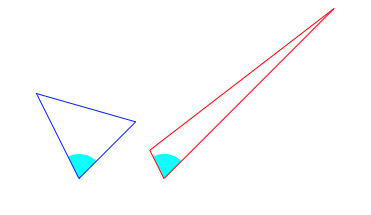
Abb. 5: Gleicher Flächeninhalt und ein gemeinsamer Winkel

Wir bringen den gemeinsamen Winkel zur Deckung. Durch Einzeichnen der schwarzen Strecke erkennen wir, dass wir es bei den oberen Teilen der beiden Dreiecke mit der Situation gleicher Grundlinie und gleicher Höhe zu tun haben (Abb. 6).

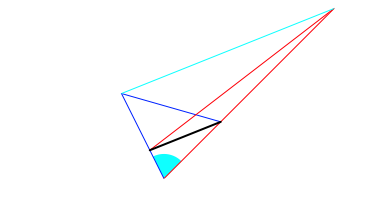
Abb. 6: Gemeinsame Grundlinie der oberen Teildreiecke

Dieses Problem haben wir bereits gelöst. Die Abbildung 7 zeigt nun einen Zerlegungsbeweis.

Abb. 7: Zerlegungsbeweis

3 Rechtecke

Wir gehen von zwei flächengleichen Rechtecken aus (Abb. 8).

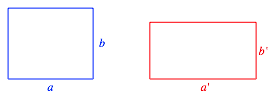
Abb. 8: Zwei flächengleiche Rechtecke

3.1 Rationale Seitenverhältnisse

Bei rationalen Seitenverhältnissen, also , gibt es ein größtes gemeinsames Teilrechteck, das die beiden Rechtecke mit der gleichen endlichen Anzahl von Teilrechtecken ausschöpft (Abb. 9).

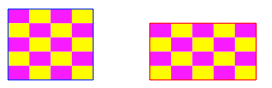
Abb. 9: Größtes gemeinsames Teilrechteck

Natürlich geht es dann auch mit weniger Puzzle-Teilen (Abb. 10).

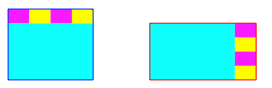
Abb. 10: Weniger Teile

3.2 Irrationale Seitenverhältnisse

Bei können wir nicht mit Rechtecken ausschöpfen.

3.2.1 Sonderfall

Wir untersuchen den Sonderfall der Abbildung 11.

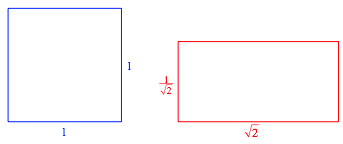
Abb. 11: Sonderfall

Der Versuch, mit Rechtecken auszuschöpfen, führt zwar zu einer interessanten Figur (Abb. 12), die aber ins Unendliche läuft.

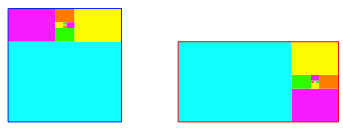
Abb. 12: Versuch einer Ausschöpfung

Die Puzzle-Teile treten mit Ausnahme des ersten paarweise auf und haben alle das Seitenverhältnis des DIN-Formates, passen aber nicht in eine DIN An Folge. Aufeinanderfolgende Teilrechtecke gehen nicht durch Halbieren oder Vierteln auseinander hervor.

Indessen lässt sich in unserem Sonderfall die Flächengleichheit mit einer Zerlegung in nur vier kongruente Puzzle Teile zeigen (Abb. 13).

Abb. 13: Zerlegungsbeweis

Und jetzt eine Hausaufgabe: Gesucht ist ein einfacher Zerlegungsbeweis für die Flächengleichheit des Einheitsquadrates und des Rechteckes mit den Seiten und für einzelne Werte von . Die Abbildung 13 ist ein Beispiel für n = 2.

3.2.2 Allgemein

Für den allgemeinen Fall halbieren wir zunächst jedes der beiden Rechtecke. Wir haben dann zwei flächengleiche rechtwinklige Dreiecke. Bei flächengleichen Dreiecken mit einem gemeinsamen Winkel wurde die Zerlegungstechnik schon besprochen. Im Folgenden die einzelnen Schritte.

Wir beginnen zwei flächengleichen Rechtecken (Abb. 14).

Abb. 14: Flächengleiche Rechtecke

Wir halbieren beide Rechtecke längs einer Diagonalen und konstruieren einen Zerlegungsbeweis (Abb. 15).

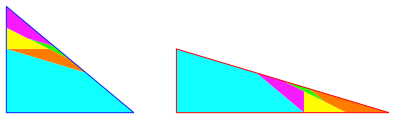
Abb. 15: Zerlegungsbeweis für halbe Rechtecke

Durch Punktspiegelung ergibt sich der Zerlegungsbeweis (Abb. 16).

Abb. 16: Zerlegungsbeweis für Rechtecke

4 Hinweise zur Hausaufgabe

Gesucht ist ein einfacher Zerlegungsbeweis für die Flächengleichheit des Einheitsquadrates und des Rechteckes mit den Seiten und für einzelne Werte von .

4.1 Quadratzahl

Für eine Quadratzahl gibt es die einfache Schachbrettlösung. Die Quadratseite und die lange Rechteckseite stehen in einem rationalen Verhältnis.

Die Abbildung 17 illustriert den Fall n = 9. Sie kann zu einer Streifenlösung vereinfacht werden (Abb. 18).

Abb. 17: Schachbrett

Abb. 18: Streifen

4.2 Summe zweier Quadratzahlen

Für den Fall gibt die Abbildung 13 eine einfache Lösung. Die Abbildung 19 zeigt eine Lösung für . Die ansteigenden schrägen Trennlinien im blauen Quadrat haben eine Steigung . Wir benötigen neun Puzzle-Teile, welche sich an einem schrägen Schachbrett orientieren.

Abb. 19: n = 5

Die Lösung lässt sich zu einer Streifenlösung mit vier Puzzle-Teilen vereinfachen (Abb. 20).

Abb. 20: Einfachere Lösung für n = 5

Die Abbildung 21 zeigt eine Lösung für . Die ansteigenden schrägen Trennlinien im blauen Quadrat haben eine Steigung .

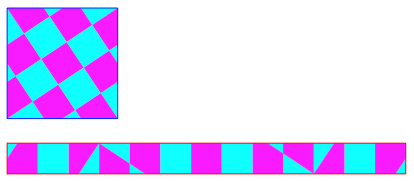
Abb. 21: n = 13

Auch diese Lösung lässt sich zu einer Streifenlösung vereinfachen (Abb. 22).

Abb. 22: Streifenlösung

Allgemein arbeiten wir für mit Streifen, welche im Quadrat die Steigung haben.

4.3 Differenz zweier Quadratzahlen

Die Abbildung 23 zeigt eine Lösung für . Die ansteigenden schrägen Trennlinien haben einen Steigungswinkel von . Die Lösung orientiert sich am schrägen Schachbrettmuster. Beim Übergang vom Quadrat zum Rechteck müssen die Puzzle-Teile um Vielfache von 30° verdreht und zum Teil (Fünfecke) sogar gespiegelt werden.

Abb. 23: n = 3

In der Lösung der Abbildung 24 können alle Puzzle-Teile vom Quadrat zum Rechteck parallel verschoben werden. Diese Lösung passt nicht so recht in das übliche Muster.

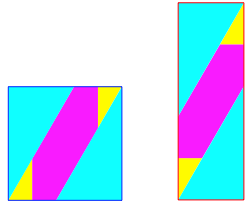
Abb. 24: n = 3

Die Abbildung 25 zeigt eine Lösung für . Die ansteigenden schrägen Trennlinien haben einen Steigungswinkel von . Die Lösung orientiert sich am schrägen Schachbrettmuster.

Abb. 25: n = 7

Die Abbildung 26 zeigt eine Variante, die sich noch stärker an die schräge Quadratrasterung anlehnt.

Abb. 26: Rastervariante

Es scheint sich da ein allgemeines Muster abzuzeichnen. Für eine Zahl von der Form müssen wir mit einem Steigungswinkel arbeiten.

Nun ist aber auch eine Differenz von Quadratzahlen. Dies führt zur Lösung der Abbildung 27, welche von der Lösung der Abbildung 19 verschieden ist. Die ansteigenden schrägen Trennlinien haben den Steigungswinkel .

Abb. 27: n = 5

Auch dieses Beispiel lässt sich verrastern (Abb. 28).

Abb. 28: Rastervariante

Für ergibt sich eine Lösung mit dem Steigungswinkel (Abb. 29).

Abb. 29: n = 9

Es ist mir nicht gelungen, eine „schöne“ Lösung für n = 11 zu finden.

4.4 Der Trick mit dem Kathetensatz

Die Abbildung 30 zeigt eine Zerlegungssituation für den Kathetensatz.

Abb. 30: Kathetensatz

Wir können nun die Situation rechts von der Höhentrennlinie für unser Problem ausnützen. Dazu zeichnen wir in einem Quadratraster der Maschenweite ein Hochformat-Rechteck der Breite und der Höhe und ergänzen zur Kathetensatz-Figur. Das zugehörige Kathetenquadrat hat dann die Seitenlänge 1. Damit haben wir eine Lösung für beliebiges n. Die Abbildung 31 illustriert das Vorgehen für n = 7.

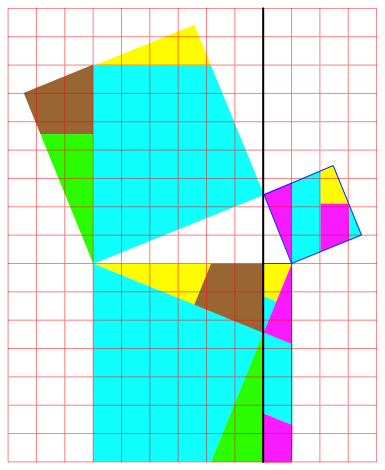
Abb. 31: Anwendung des Kathetensatzes

Die Abbildung 32 zeigt die aus der Abbildung 31 isolierte Lösung für n = 7. Es ist dabei noch geeignet gedreht und gespiegelt worden. Die Lösung weicht ab von den symmetrischen Lösungen der Abbildungen 25 und 26.

Die ansteigenden schrägen Linien haben die Steigung .

Abb. 32: n = 7

4.5 Der Trick mit dem Höhensatz

Die Abbildung 33 zeigt eine Zerlegungssituation für den Höhensatz. Die ansteigenden Schrägen sind parallel zu einer Kathete.

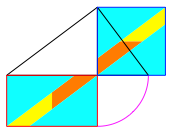
Abb. 33: Höhensatz

Wir können dies für unser Problem ausnützen. Dazu zeichnen wir in einem Quadratraster der Maschenweite ein Querformat-Rechteck der Breite und der Höhe und ergänzen zur Höhensatz-Figur. Das zugehörige Höhenquadrat hat dann die Seitenlänge 1. Damit haben wir eine Lösung für beliebiges n. Die Abbildung 34 illustriert das Vorgehen für n = 7.

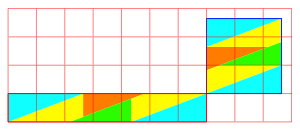
Abb. 34: n = 7

Schließlich doch noch eine Lösung für n = 11 (Abb. 35).

Abb. 35: n = 11

Die Abbildung 36 zeigt dasselbe mit einem zerhackten Raster.

Abb. 36: Zerhackter Raster