Hans Walser, [20180401]

Zimmermannsknoten

1 Worum es geht

Es wird versucht, den bekannten Zimmermannsknoten so zu variieren, dass wir mit sechs kongruenten Teilen auskommen.

2 Der klassische Zimmermannsknoten

2.1 Ansicht

Die Abbildung 1 zeigt den klassischen Zimmermannsknoten in zusammengebautem Zustand. Da sieht man nicht viel.

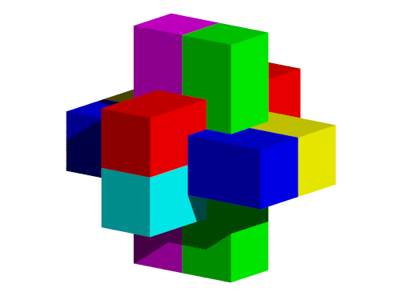
Abb. 1: Zimmermannsknoten zusammengebaut

2.2 Bauteile

Die Abbildung 2 zeigt die sechs Einzelteile in einer Explosionsdarstellung.

Abb. 2: Die sechs Einzelteile

Die Einzelteile sind nicht alle gleich.

Die Abbildung 3 zeigt die Teile grün und magenta. Diese beiden Teile sind gleich.

Abb. 3: Teile grün und magenta

Die Abbildung 4 zeigt die Teile blau und gelb. Diese Teile sind untereinander gleich, aber verschieden von den Teilen grün und magenta. Sie sind, aus meiner Sicht, die kompliziertesten Teile.

Abb. 4: Teile blau und gelb

Die Abbildung 5 schließlich zeigt die Teile zyan und rot.

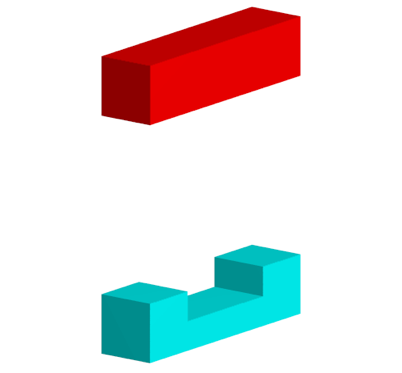
Abb. 5: Teile zyan und rot

Diese beiden Teile sind unterschiedlich. Der Teil zyan ist gleich den Teilen grün und magenta. Der Teil rot ist ein Vierkant mit quadratischem Querschnitt.

Soweit die Einzelteile.

2.3 Zusammenbau

Der Zusammenbau geschieht folgendermaßen. Wir beginnen mit dem Teil zyan und fügen auf beiden Seiten die Teile grün und magenta symmetrisch an (Abb. 6).

Abb. 6: Beginn des Zusammenbaus

Nun schieben wir seitlich die Teile blau und gelb gemäß Abbildung 7 ein.

Abb. 7: Einschieben der Teile blau und gelb

Diese beiden Teile können wir nun herunterschieben, bis sie auf dem Teil zyan aufsitzen (Abb. 8).

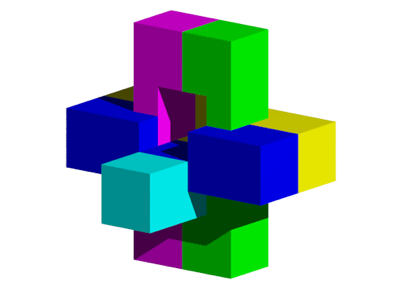
Abb. 8: Herunterschieben der Teile blau und gelb

Nun bleibt ein Loch mit quadratischem Profil übrig, in das wir den roten Teil seitlich einschieben können. Dann haben wir die Lösung gemäß Abbildung 1.

3 Die unlösbare Lösung

Sechs gleiche Teile vom Typ zyan, grün oder magenta passen zwar ebenfalls zur Figur der Abbildung 1 zusammen. Im Innern bleibt ein würfelförmiger Hohlraum übrig. Das Problem ist, dass es unmöglich ist, sechs separat gegebene Teile zur Figur zusammenzufügen, ohne einen Teil zu zerlegen (etwa eine äußere Noppe abschneiden und nachher wieder anfügen).

Um den würfelförmigen Hohlraum aufzufüllen, kann bei jedem Teil noch eine Pyramide gemäß Abbildung 9 angebaut werden. Aber auch damit können die Teile natürlich nicht zusammengebaut werden, obwohl sie „passen“.

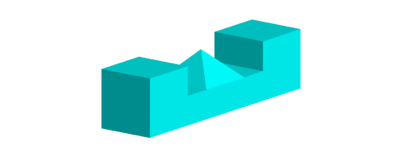
Abb. 9: Anbau einer Pyramide

4 Modifikation

Wir modifizieren den Bauteil der Abbildung 9 zum Bauteil der Abbildung 10.

Abb. 10: Modifikation

Unten wird auf beiden Seiten ein Keil abgeschnitten, der oben wieder angefügt wird. Der Bauteil hängt immer noch massiv zusammen. Er ist „am Stück“.

5 Zusammenschieben

Mit sechs solchen Bauteilen können wir den Zimmermannsknoten zusammenbauen. Allerdings müssen wir die sechs Bauteile simultan einschieben. Wir brauchen also sechs Hände dazu.

Die Abbildung 11 zeigt eine Startposition.

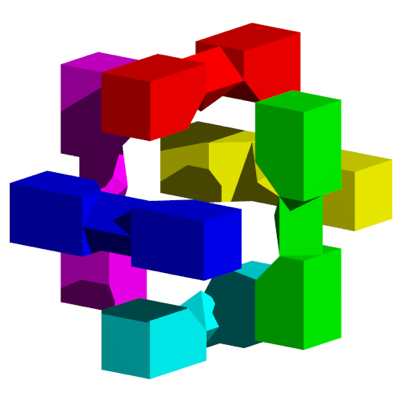
Abb. 11: Startposition

In der Abbildung 12 haben sich alle Teile gleich weit dem Zentrum angenähert. Wir sehen, wie die durch die Modifikation entstandenen Schrägen aufeinander zukommen.

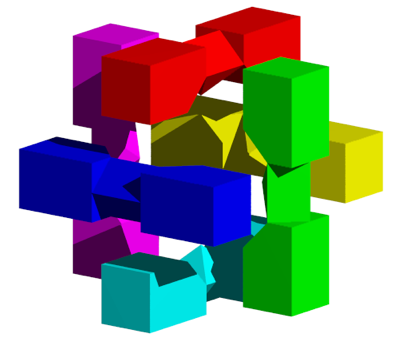
Abb. 12: Stalldrang

In den Abbildungen 13 und 14 haben sich die Teile weiter dem Zentrum angenähert.

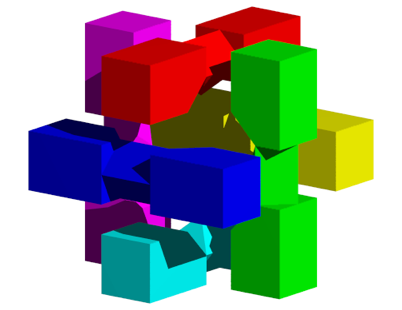
Abb. 13: Warm

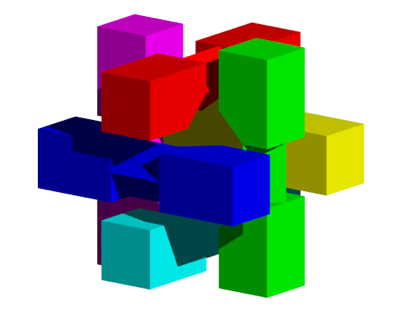
Abb. 14: Wärmer

In der Abbildung 15 sehen wir den Moment der Kontaktaufnahme.

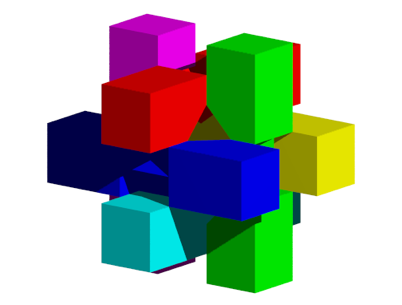
Abb. 15: Kontaktaufnahme

Nun gleiten die in der Modifikation eingefügten Schrägebenen aufeinander (Abb. 16).

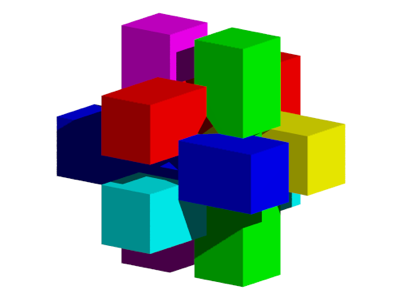
Abb. 16: Schrägebenen gleiten aufeinander

In der Abbildung 17 ist die Endlage erreicht. Das äußere Ansehen entspricht der Abbildung 1.

Abb. 17: Endlage

Damit ist das Eingangsproblem gelöst.

6 Weitere Modifikationen

6.1 Anfasen

Die Abbildung 18 zeigt eine weitere Modifikation. Gegenüber der Figur der Abbildung 10 sind die Längskanten angefast (das heißt auf 45° abgeschrägt) und der Bauteil verkürzt. Die relevante Konfiguration im Zentrum ist beibehalten.

Abb. 18: Weitere Modifikation

Mit sechs Teilen der Abbildung 18 kann ebenfalls ein Zimmermannsknoten hergestellt werden. Die Abbildung 19 zeigt eine mögliche Startposition, die Abbildung 20 die Endlage. Dieser Knoten wird gelegentlich als kanadischer Zimmermannsknoten bezeichnet.

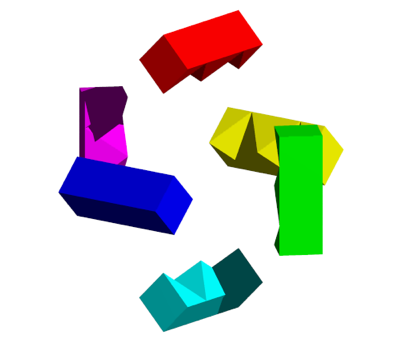
Abb. 19: Startposition

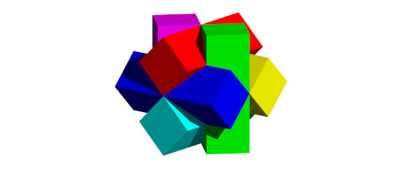
Abb. 20: Endlage

6.2 „Schiffchen“

Die Abbildung 21 zeigt eine schiffchenförmige Modifikation der Figur der Abbildung 18.

Abb. 21: „Schiffchen“

Die Abbildung 22 zeigt eine Startposition mit sechs Teilen, die Abbildung 23 die Endlage.

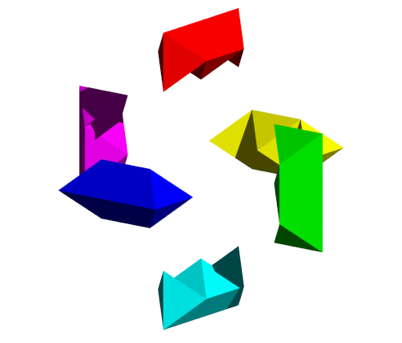
Abb. 22: Startposition

Abb. 23: Endlage

Die Endlage ist eine Art Stern mit zwölf Spitzen. Die Abbildung 24 zeigt diesen Stern monochrom.

Abb. 24: Roter Stern

Dieser Stern ist ein Raumfüller. Wir können damit den Raum lückenlos und überlappungsfrei auffüllen.

Die Abbildung 25 zeigt eine würfelförmige Anordnung.

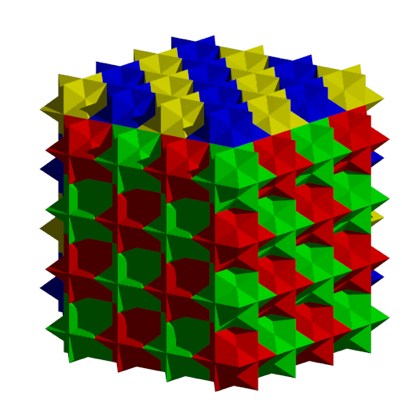
Abb. 25: Sternenkubus

Die Abbildung 26 gibt eine pyramidale Anordnung.

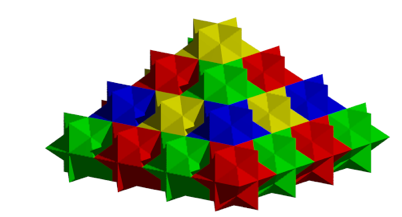
Abb. 26: Pyramidale Anordnung