Hans Walser, [20200523]

Zwei Quadrate

1 Worum geht es?

Spiel mit zwei gelenkig verbundenen Quadraten.

2 Grundfigur

Wir arbeiten mit zwei Quadraten der Seitenlängen a und b mit a > b, welche an einer Ecke gelenkig verbunden sind. Die Abbildung 1 zeigt drei verschiedenen Positionen.

Abb. 1: Grundfigur in verschiedenen Positionen

3 Quadrate diagonal einpassen

Wir passen nun zwei weitere Quadrate diagonal ein.

3.1 Beispiel 1

Aus der Position der Abbildung 1a) ergibt sich die Figur der Abbildung 2.

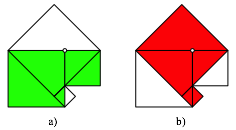
Abb. 2: Diagonal eingepasste Quadrate

Nun gilt: Die rote Flächensumme ist gleich der grünen Flächensumme. Rot = Grün.

Die Abbildung 3 zeigt einen Zerlegungsbeweis.

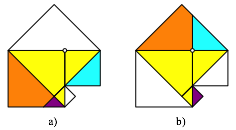
Abb. 3: Zerlegungsbeweis

Für den rechnerischen Beweis eine Vorbemerkung: Der Flächeninhalt eines Quadrates mit der Seitenlänge s ist s². Der Flächeninhalt eines Quadrates mit der Diagonalen d ist (Abb. 4).

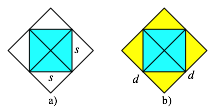
Abb. 4: Quadratfläche

Frage 1: Warum kann die Rechteckfläche nicht aus den Diagonalen berechnet werden? Bei welchen Vierecken kann der Flächeninhalt sehr einfach als halbes Produkt aus den Diagonalen berechnet werden?

Die grünen Quadrate der Abbildung 2a) haben die Seiten a beziehungsweise b. Die roten Quadrate der Abbildung 2b) haben die Diagonalen beziehungsweise . Für ihre Flächensumme ergibt sich daher:

(1)

Die rote Flächensumme ist also gleich der grünen Flächensumme.

3.2 Beispiel 2

Aus der Position der Abbildung 1b) ergibt sich die Figur der Abbildung 5. Die roten Quadrate werden diagonal an denjenigen Ecken der grünen Quadrate eingepasst, welche an den Gelenkpunkt anschließen. Das war schon bei der Abbildung 2 so, aber dort sieht man es nicht so gut.

Interessant ist bei der Abbildung 5b), dass auch die beiden roten Quadrate einen Eckpunkt gemeinsam haben. Wir werden das im allgemeinen Beispiel wieder antreffen und beweisen.

Wiederum ist die rote Flächensumme gleich der grünen Flächensumme.

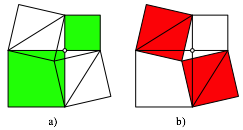
Abb. 5: Rot = Grün

Rechnerischer Beweis mit dem Satz des Pythagoras: Für die Diagonalen d der roten Quadrate gilt:

(2)

Somit gilt für die rote Flächensumme:

(3)

Die Abbildung 6 visualisiert die zweimalige halbe Anwendung des Satzes des Pythagoras.

Abb. 6: Satz des Pythagoras

3.3 Beispiel 3

Aus der allgemeinen Position der Abbildung 1c) ergibt sich die Figur der Abbildung 7. Wird dies mit einer dynamischen Geometrie-Software gezeichnet, lässt sich leicht verifizieren, dass die rote Flächensumme wiederum gleich der grünen Flächensumme ist. Und wiederum haben die beiden roten Quadrate eine Ecke gemeinsam.

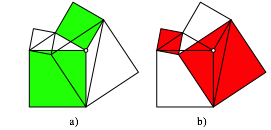
Abb. 7: Rot = Grün

Für den Beweis der Flächensummeneigenschaft berechnen wir die Diagonalen d und e der beiden roten Quadrate (Abb. 8). Dazu verwenden wir das rechtwinklige orange Dreieck.

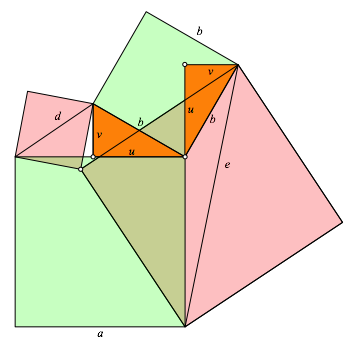
Abb. 8: Diagonalen

Es ist:

(4)

Daraus ergibt sich:

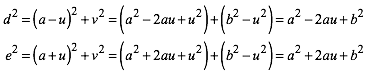(5)

Für die rote Flächensumme erhalten wir:

(6)

Damit ist die rote Flächensumme gleich der grünen Flächensumme.

Nun berechnen wir die Position des rechten unteren Eckpunktes des kleinen roten Quadrates (Abb. 9).

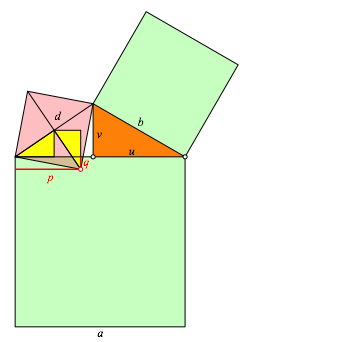
Abb. 9: Position der Ecke des kleinen roten Quadrates

Das gelbe rechtwinklige Dreieck hat die lange Kathete und die kurze Kathete . Daraus ergibt sich:

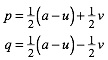(7)

Analog berechnen wir die Position des linken oberen Eckpunktes des großen roten Quadrates (Abb. 10).

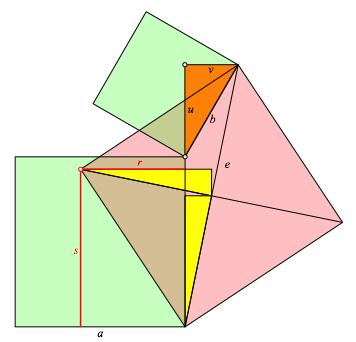
Abb. 10: Position der Ecke des großen roten Quadrates

Das rechtwinklige Dreieck hat hier die lange Kathete und ebenfalls die kurze Kathete . Daraus ergibt sich:

(8)

Aus (7) und (8) folgt:

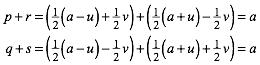(9)

Das heißt aber, dass die betrachteten Eckpunkte der beiden roten Quadrate zusammenfallen.

Unsere Figur ist also strukturell symmetrisch (Abb. 11a). Wir können jetzt ebenso gut sagen, dass die roten Quadrate an einer Ecke verbunden sind und die grünen diagonal eingespannt.

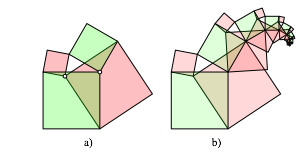
Abb. 11: Symmetrie. Spirale

Frage 2: Wie ist die Spirale der Abbildung 11b) entstanden?

4 Ausblick

Einige weitere Eigenschaften der Figur der Abbildung 11a), ohne Beweise.

4.1 Verbindungsstrecken

Die Abbildung 12a) enthält die Verbindungsstrecken der Außenecken der Quadrate. Diese Strecken sind gleich lang und rechtwinklig. Sie verlaufen durch die Gelenkpunkte der Gegenfarbe und werden durch diese halbiert.

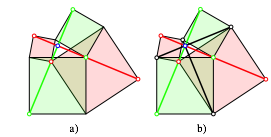
Abb. 12: Verbindungsstrecken

In der Abbildung 12b) sind weitere Verbindungsstrecken eingezeichnet. Sie sind untereinander gleich lang und orthogonal und schneiden sich im Schnittpunkt der Verbindungsstrecken der Abbildung 12a). Sie schließen zu diesen Verbindungsstrecken Winkel von 45° ein. Die Länge der Verbindungsstrecken der Abbildung 12a) ist das der Länge der schwarzen Verbindungsstrecken der Abbildung 12b).

4.2 Umkreise

Die Umkreise der vier Quadrate verlaufen durch einen gemeinsamen Punkt (Abb. 13a), nämlich durch den Schnittpunkt der Verbindungsstrecken der Abbildung 12.

Abb. 13: Umkreise

Die Zentren der Umkreise bilden ein Quadrat (Abb. 13b).

5 Bearbeitung der Fragen

Bearbeitung der Frage 1: Genau bei Vierecken mit rechtwinkligen Diagonalen ist der Flächeninhalt das halbe Produkt der Diagonalenlängen. Die Abbildung 14 zeigt Beispiele. Dazu gehören die Raute und das Drachenviereck, aber noch weitere Vierecke.

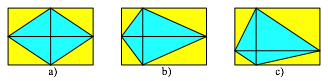
Abb. 14: Vierecke mit rechtwinkligen Diagonalen

Bearbeitung der Frage 2: Das dritte grüne Quadrat verhält sich zum zweiten wie dieses zum ersten. Und so weiter.

Websites

Hans Walser: Im rechtwinkligen Dreieck

http://www.walser-h-m.ch/hans/Miniaturen/R/Rechtw_Dreieck/Rechtw_Dreieck.htm

Hans Walser: Orthodiagonale Vierecke

www.walser-h-m.ch/hans/Miniaturen/O/Orthodiag_Vierecke/Orthodiag_Vierecke.htm

Hans Walser: Orthogonale Diagonale

www.walser-h-m.ch/hans/Miniaturen/O/Orthogonale_Diagonalen/Orthogonale_Diagonalen.htm

Hans Walser: Zwei Quadrate

http://www.walser-h-m.ch/hans/Miniaturen/Z/Zwei_Quadrate/Zwei_Quadrate.htm