Hans Walser, [20160118]

Zweiecke als Deltakurven

Idee: Renato Pandi

1     Worum geht es

Eine Delta-Kurve ist eine geschlossene Kurve, die sich beliebig in einem gleichseitigen Dreieck (ãDeltaÒ) verdrehen lŠsst. Dabei sollen immer alle drei Dreieckseiten von der Kurve berŸhrt werden.

Bogen-Zweiecke mit Winkeln von 60¡ oder 120¡ sind solche Deltakurven.

Es wird gezeigt, dass es unter den Delta-Kurven keine anderen konvexe Bogen-Zweiecke gibt.

2     Disposition

Das Bogen-Zweieck habe den Bogenradius 1 und den Zentriwinkel  fŸr jeden der beiden Bšgen. Es gelten dann die in der Abbildung 1 eingetragenen Beziehungen.  

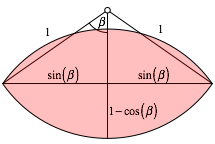
Abb. 1: Das Zweieck

An den beiden Ecken hat das Bogen-Zweieck dann die Innenwinkel . (Der Innenwinkel ergibt sich durch die Tangenten an die Kreisbšgen in der Ecke des Zweiecks.)

3     Fallunterscheidung

Wir unterscheiden folgende drei FŠlle bezŸglich des Winkels :

1.  (ãZahnstocherÒ)

2.  (ãmittleres ZweieckÒ)

3.  (ãdicke ZweieckeÒ)

Die Fallunterscheidungen sind nicht disjunkt, sondern haben gemeinsame Grenzen.

In jedem der drei FŠlle zeichnen wir das Bogen-Zweieck im Querformat und im Hochformat und umschreiben ein gleichseitiges Dreieck. Falls das zur Diskussion stehende Bogen-Zweieck eine Delta-Kurve ist, mŸssen die beiden umbeschriebenen Dreiecke dieselbe Hšhe haben. Damit haben wir eine notwendige Bedingung fŸr die zulŠssigen Winkel .

3.1    Zahnstocher

Es ist also . Die Abbildung 2 zeigt das Beispiel fŸr .

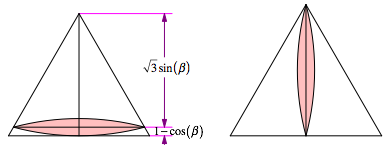
Abb. 2: Zahnstocher. beta = 15¡

FŸr den Zahnstocher im Querformat erhalten wir die Dreieckshšhe:

 

                                                                                           (1)

 

FŸr den Zahnstocher im Hochformat erhalten wir die Dreieckhšhe:

 

                                                                                                               (2)

 

Die Bedingung  liefert die Gleichung:

 

                                                                                       (3)

 

Die Gleichung (3) hat im Intervall  die Lšsung:

 

                                                                                                                               (4)

 

Das ist die Rand-Lšsung.

3.2    Mittleres Zweieck

Es ist: . Die Abbildung 3 zeigt das Beispiel fŸr .

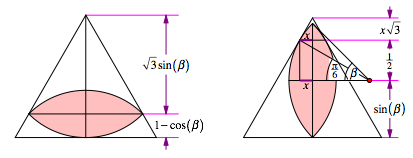
Abb. 3: beta = 45¡

Beim Bogen-Zweieck im Querformat ergibt sich die Dreieckshšhe wie bei (1):

 

                                                                                           (5)

 

FŸr das Hochformat berechnen wir zunŠchst die Hilfsgrš§e x:

 

                                                                                 (6)

 

Damit erhalten wir die Dreieckshšhe:

 

                                   (7)

 

Gleichsetzen der beiden Hšhen liefert:

 

                                                               (8)

 

Die Gleichung (8) hat im Intervall  die beiden Lšsungen:

 

                                                        und                                                   (9)

 

Das sind die beiden Rand-Lšsungen.

3.3    Dickes Zweieck

Es ist . Die Abbildung 4 zeigt das Beispiel fŸr .

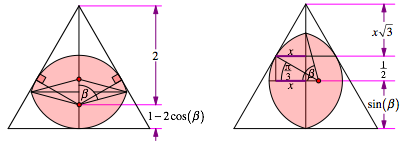
Abb. 4: Dickes Zweieck. beta = 75¡

Beim Querformat erhalten wir die Dreieckshšhe:

 

                                                                           (10)

 

FŸr das Hochformat benštigen wir wiederum die Hilfsgrš§e (6) und erhalten die Dreieckshšhe wie bei (7):

 

                                 (11)

 

Gleichsetzen liefert:

 

                                                                           (12)

 

Die Gleichung (12) hat im Intervall  die beiden Rand-Lšsungen:

 

                                                        und                                                 (13)

 

Somit haben wir als einzige Lšsungen die Bogen-Zweiecke mit Innenwinkeln von 60¡, 120¡ und 180¡. Letzteres ist der Inkreis des Dreiecks.