Hans Walser, [20180605]
Zwlfknotenschnur
1 Die Unwahrheit
Eine der harmloseren Unwahrheiten im Mathematikunterricht ist die Behauptung, die alten gypter htten den rechten Winkel mit der Zwlfknotenschnur modelliert (Abb. 1a). Diese Behauptung lsst sich nicht belegen. Sie widerspricht auch handwerklichen Grundprinzipien (Przision und Sicherheit, einfache und schnelle Handhabung) der Vermessungstechnik.
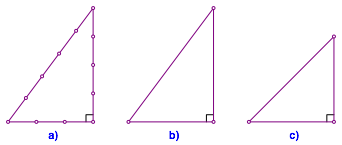
Abb. 1: Knotenschnre
Tatschlich htte eine Dreiknotenschnur (Abb. 1b) gengt und wre viel handlicher gewesen. Man bruchte nicht bei jedes Mal die Knoten abzuzhlen. Noch einfacher ist eine Dreiknotenschnur mit zwei gleichlangen Abschnitten (Abb. 1c). Der dritte, lngere Abschnitt lsst sich leicht mit Symmetrietechniken ermitteln und setzt in der Praxis den Satz des Pythagoras nicht voraus.
Dennoch hat die Zwlfknotenschnur ein gro§es Didaktisches Potential.
2 Verzhlen
Man kann sich beim Abzhlen der Knoten vertun (Abb. 2). Welche Winkel entstehen dabei?
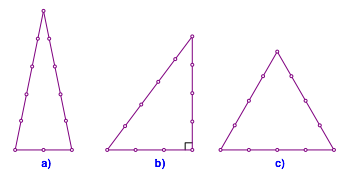
Abb. 2: Falsches Abzhlen
3 Halbrunde Auslegeordnung
Wenn wir die Zwlfknotenschnur halbrund auslegen (Abb. 3a), haben wir auch eine Visualisierung des Flchensatzes von Pythagoras. Rot ist gleich gro§ wie blau plus blau.
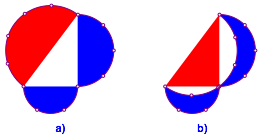
Abb. 3: Flchensatz. Mndchen
Bei den Mndchen des Hippokrates gibt es ein Problem: Beim rechten Winkel sitzen die Punkte nicht richtig. Lsst sich das Problem beheben, indem wir mit anderen pythagoreischen Dreiecken arbeiten?
4 Kreisrunde Auslegeordnung
Mit der kreisrunden Auslegeordnung (Abb. 4) knnen wir verschiedenen Figuren bauen, welche an den Knoten orientiert sind. Dabei muss allerdings klar sein, dass eine runde Anordnung dem Grundsatz des Seilspannens widerspricht und daher eher theoretischen berlegungen entspricht.
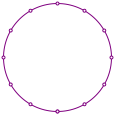
Abb. 4: Kreisrunde Auslegeordnung
4.1 Thaleskreis und Ortsbogen
Wir knnen alte Bekannte exemplarisch illustrieren.
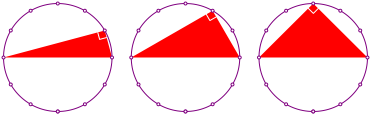
Abb. 5: Thaleskreis
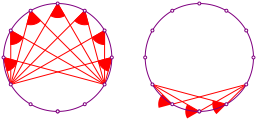
Abb. 6: Ortsbogen
4.2 Schnittpunkte
Stimmen die in der Abbildung 7 dargestellten Schnittpunkte?
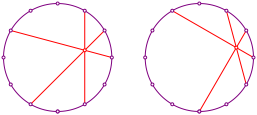
Abb. 7: Schnittpunkte
ber Schnittpunkte siehe Walser (2012).
4.3 Kreisfiguren in der Ebene

Abb. 8.1: Kreisfigur

Abb. 8.2: Kreisfigur
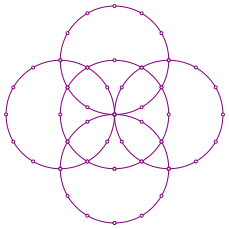
Abb. 8.3: Kreisfigur

Abb. 8.4: Kreisfigur

Abb. 8.5: Kreisfigur

Abb. 8.6: Kreisfigur

Abb. 8.7: Kreisfigur
4.4 Kreisfiguren im Raum und auf der Kugel
4.4.1 Gro§kreise
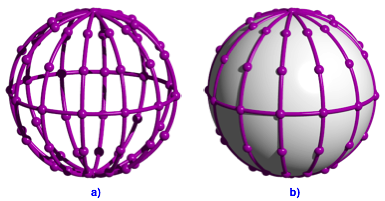
Abb. 9: quator und Meridiane
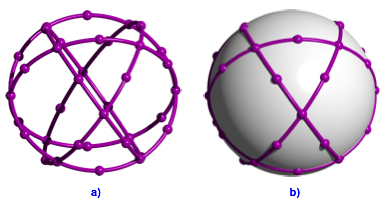
Abb. 10: Kreisfigur mit Gro§kreisen
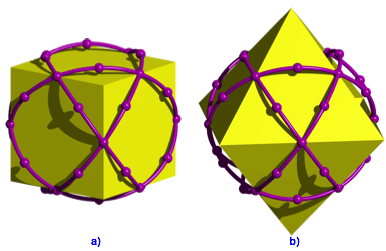
Abb. 11: Mit Wrfel und Oktaeder
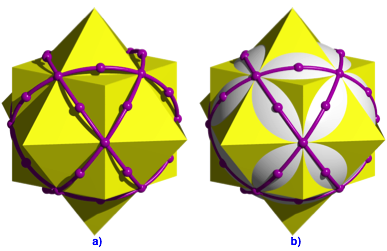
Abb. 12: Das volle Programm
4.4.2 Kleinkreise
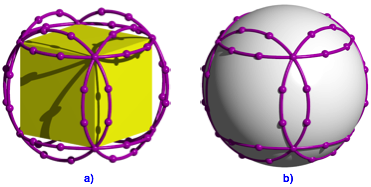
Abb. 13: Kleinkreise am Wrfel
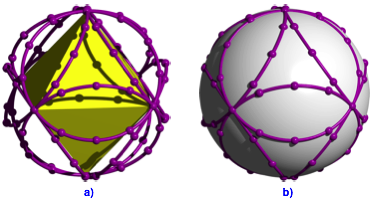
Abb. 14: Kleinkreise am Oktaeder
4.4.3 Gro§- und Kleinkreise
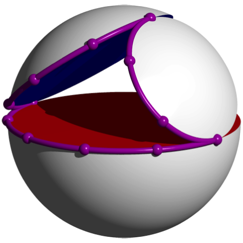
Abb. 15: Ein Gro§kreisbogen und zwei Kleinkreisbgen
Literatur
Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0.