Hans Walser, [20070901a]

Zyklische Fibonacci-Folgen

Anregung: [Weihmann 1996]

1 Worum es geht

In [Weihmann 1996, S. 5] wird gezeigt, dass die in definierte Rekursion

stets einen Zwölfer-Zyklus ergibt. Mit den allgemeinen Startwerten und gilt nämlich:

z[0] = p + I*q

z[1] = r + I*s

z[2] = p + I*q + I*r - s

z[3] = I*p - q

z[4] = I*r - s

z[5] = I*p - q - r - I*s

z[6] = - p - I*q

z[7] = - r - I*s

z[8] = s - I*q - I*r - p

z[9] = q - I*p

z[10] = s - I*r

z[11] = q - I*p + r + I*s

z[12] = p + I*q

z[13] = r + I*s

So erhalten wir etwa mit den Startwerten und in der Gaußschen Zahlenebene die folgende Figur:

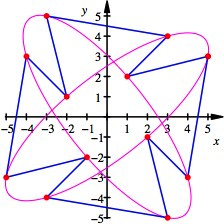
Zyklische Figur

Die Punkte liegen offenbar alternierend auf zwei Ellipsen.

Wir können dieses Beispiel auf beliebige geradzahlige Zyklenlängen verallgemeinern.

2 Zyklenlänge n

Es sei , und . Dann führt die reelle Rekursion

bei beliebigen Startwerten zu einer Folge mit der Zyklenlänge n.

Beweis:

Für die n-ten Einheitswurzeln gilt:

Dies kann durch Einsetzen verifiziert werden:

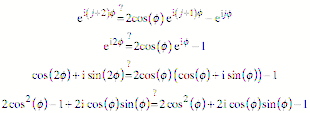
Die Rekursion liefert also mit den Startwerten und genau die n-ten Einheitswurzeln . Die Folge ist zyklisch mit der Zyklenlänge n; und in der Gaußschen Ebene erhalten wir das reguläre n-Eck.

Zu zwei beliebigen Startwerten und verwenden wir nun die affine Abbildung mit dem Fixpunkt im Ursprung, welche durch und definiert ist. Da die Rekursion affin invariant ist, erhalten wir:

Die Folge ist also ebenfalls zyklisch mit der Zyklenlänge n. Die Punkte bilden in der Gaußschen Ebene ein affin-reguläres n-Eck (affines Bild eines regulären n-Eckes).

2.1 Bemerkungen

2.1.1 Reelle Rekursion

Die Rekursion ist reell; mit reellen Startwerten erhalten wir eine reelle zyklische Folge.

2.1.2 Affine Abbildung

Mit den Startwerten und ist die affine Abbildung durch folgende Matrix gegeben:

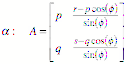
2.1.3 Außenellipse

Das affine Bild des Einheitskreises wird zur Außenellipse des affin-regulären n-Eckes. Diese Ellipse hat die Parameterdarstellung:

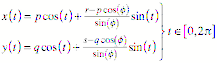
2.2 Beispiel

Für ist und . Wir haben also die Rekursion:

Mit den allgemeinen Startwerten und gilt:

a[0] = p + I*q

a[1] = r + I*s

a[2] = r - I*q - p + I*s

a[3] = - p - I*q

a[4] = - r - I*s

a[5] = p + I*q - r - I*s

a[6] = p + I*q

a[7] = r + I*s

Insbesondere erhalten wir mit den Startwerten und in der Gaußschen Zahlenebene die folgende Figur:

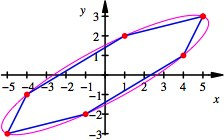
Affin-reguläres Sechseck

3 Zyklenlänge 2n

Zu , sei nun ; es ist also . Dann führt die in definierte Rekursion

bei beliebigen Startwerten zu einer Folge mit der Zyklenlänge 2n.

Beweis:

Wir berechnen in Abhängigkeit von und . Zunächst ist:

Aus der Rekursion ergibt sich:

Wir setzen dies oben ein und erhalten:

Nun ist aber:

Somit haben wir bei Schrittlänge 2 die reelle Rekursion:

Das entspricht aber der oben besprochenen Rekursion . Daher sind die Teilfolgen (gerade Indizes) und (ungerade Indizes) je zyklisch mit der Zyklenlänge n. In der Gaußschen Ebene bilden sie je ein affin-reguläres n-Eck und liegen auf einer Ellipse.

Die Gesamtfolge ist zyklisch mit der Zyklenlänge 2n.

3.1 Beispiel n = 6

Für ist . Wir erhalten die in [Weihmann 1996] und im Eingangsbeispiel besprochene Rekursion .

3.2 Beispiel n = 7

Für und die Startwerte und erhalten wir:

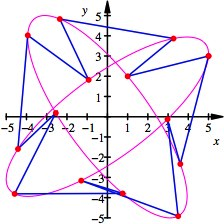
n = 7

Die Punkte liegen abwechslungsweise auf zwei Ellipsen; die Figur hat aber keine Symmetrien.

Die Beispiele zeigen, dass diese beiden Ellipsen immer kongruent und um verdreht sind. Dies konnte ich bis jetzt nicht beweisen.

Literatur

[Weihmann 1996] Weihmann, Christopher: Fibonacci-Folgen im komplexen Zahlbereich. Mathematisch-physikalische Korrespondenz, Nr. 187, Weihnachten 1996, S. 3-26