Hans Walser, [20100221b]
Zykloide
1 Parameterdarstellung
Wir gehen aus von der
Parameterdarstellung:
![]()
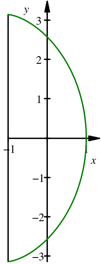
Zykloide
Der Einheitskreis rollt
auf der Geraden ![]() im positiven
Drehsinn hinauf. Die Zykloide ist symmetrisch zur x-Achse gezeichnet.
im positiven
Drehsinn hinauf. Die Zykloide ist symmetrisch zur x-Achse gezeichnet.
2
Längenberechnung
Aus der
Parameterdarstellung erhalten wir:
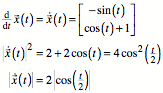
Im Definitionsbereich ![]() können die
Betragsstriche weggelassen werden. Für die Bogenlänge s ergibt sich:
können die
Betragsstriche weggelassen werden. Für die Bogenlänge s ergibt sich:
![]()
Für den
Definitionsbereich ![]() ergibt sich der
Wertebereich
ergibt sich der
Wertebereich ![]() .
.
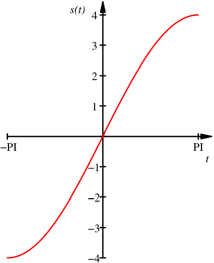
Kurvenlänge
Wir sehen, dass der
Zykloidenbogen die Länge 8 hat.
3
Natürlicher Parameter
Wir parametrisieren die
Zykloide mit der eigenen Bogenlänge. Aus ![]() erhalten wir:
erhalten wir:
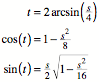
Eingesetzt in die
Parameterdarstellung ergibt die Parameterdarstellung im natürlichen Parameter s:
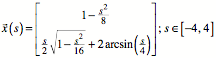
4
Richtung und Krümmung
In natürlichen
Parametern lassen sich Richtung und Krümmung sehr einfach berechnen.
Für die Ableitung nach s verwenden wir das Strich-Symbol.
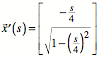
Daraus ergibt sich ![]() , was den natürlichen Parameter charakterisiert.
, was den natürlichen Parameter charakterisiert.
4.1
Richtung
Für den Richtungswinkel
![]() der Zykloide
ergibt sich aus dem Tangentialvektor
der Zykloide
ergibt sich aus dem Tangentialvektor ![]() :
:
![]()
Der Richtungswinkel
dreht von 0 auf π, was sich ja auch aus der Zykloidenfigur ergibt.
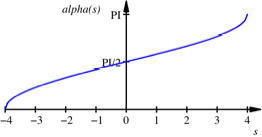
Richtungswinkel
4.2
Bezug zum ursprünglichen Parameter t
Aus ![]() und
und ![]() ergibt sich:
ergibt sich:
![]()
4.3
Krümmung
Die Krümmung ![]() ist die Richtungsänderung relativ zum Kurvenfortschritt,
also:
ist die Richtungsänderung relativ zum Kurvenfortschritt,
also:
![]()
Andererseits ist:
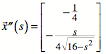
Daraus ergibt sich:
![]()
Das ist offensichtlich
die Krümmung. Allgemein ist bei natürlichen Parametern ![]() . In unserem Beispiel ist die Krümmung positiv.
. In unserem Beispiel ist die Krümmung positiv.
5
Radlinien
Die Zykloide ist selber
eine Radlinie. Wir lassen nun zusätzlich auf der Zykloide ein Rad mit dem
Radius ![]() oder einem
Bruchteil davon abrollen. Der Radius ist so gewählt, dass es „aufgeht“.
oder einem
Bruchteil davon abrollen. Der Radius ist so gewählt, dass es „aufgeht“.
5.1
Radlinie rechts
5.1.1
Ein Bogen
Wir wählen ![]() . Das Rad macht einen Umlauf, es gibt einen Bogen.
. Das Rad macht einen Umlauf, es gibt einen Bogen.
Es sei ![]() der um
der um ![]() gedrehte Vektor
gedrehte Vektor ![]() , also:
, also:
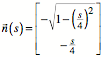
Dieser Vektor weist auf
die linke Seite der Zykloide. Somit beschreibt ![]() den Weg des
Mittelpunktes des auf der rechten Seite der Zykloide abrollenden Rades. Um den
Weg eines Punktes auf der Peripherie des Rades zu verfolgen, brauchen wir noch
den Drehwinkel
den Weg des
Mittelpunktes des auf der rechten Seite der Zykloide abrollenden Rades. Um den
Weg eines Punktes auf der Peripherie des Rades zu verfolgen, brauchen wir noch
den Drehwinkel ![]() des Rades. Bei
Abrollen auf einer Geraden ist
des Rades. Bei
Abrollen auf einer Geraden ist ![]() , wobei
, wobei ![]() eine additive
Justierkonstante ist. Bei Abrollen auf einer gekrümmten Kurve kommt aber noch
die Krümmung, also die Veränderung der Kurvenrichtung dazu:
eine additive
Justierkonstante ist. Bei Abrollen auf einer gekrümmten Kurve kommt aber noch
die Krümmung, also die Veränderung der Kurvenrichtung dazu:
![]()
Am Anfang, also bei ![]() , muss der Drehwinkel
, muss der Drehwinkel ![]() sein, wenn wir
den Weg des anfänglichen Berührungspunktes des Rades mit der Zykloide als
Radlinie haben möchten. Daraus ergibt sich.
sein, wenn wir
den Weg des anfänglichen Berührungspunktes des Rades mit der Zykloide als
Radlinie haben möchten. Daraus ergibt sich.
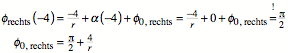
Somit ist:
![]()
Somit erhalten wir für
die Radlinie die Parameterdarstellung im Parameter s:
![]()
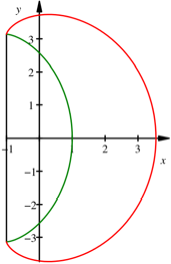
Radlinie rechts auf der
Zykloide
Der Parameter s ist aber nicht die Bogenlänge der Radlinie. Diese
ist ja länger als die Zykloide. Numerisch ergibt sich:
![]()
Leider konnte meine
Software das Längenintegral nicht exakt lösen.
5.1.2
Mehrere Bogen
Wir wählen ![]() , es gibt also m
Bogen. Die Abbildung zeigt den Fall
, es gibt also m
Bogen. Die Abbildung zeigt den Fall ![]() .
.
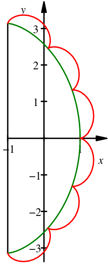
Sechs Bogen
Die einzelnen Bögen
sind unterschiedlich lang:
Bogenlänge rechts [1] = 1.87939424
Bogenlänge rechts [2] = 1.802403437
Bogenlänge rechts [3] = 1.789264826
Bogenlänge rechts [4] = 1.789264826
Bogenlänge rechts [5] = 1.802403437
Bogenlänge rechts [6] = 1.87939424
Für die Gesamtlänge
erhalten wir:
Summe der Bogenlängen rechts =
10.94212501 = 68.75139907/(2*PI)
Für ![]() erhalten wir:
erhalten wir:
Summe der Bogenlängen rechts =
10.23547712 = 64.31139947/(2*PI)
Für ![]() ergibt sich:
ergibt sich:
Summe der Bogenlängen rechts =
10.19096602 = 64.03172794/(2*PI)
Vermutlich gilt:
![]()
5.2
Radlinie links
Analog können wir für
Radlinien links vorgehen. Das Rad dreht nun im negativen Drehsinn.
5.2.1
Ein Bogen
Wir wählen wiederum ![]() . Es ist:
. Es ist:
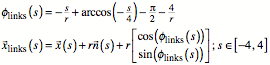
Die Abbildung zeigt
beide Radlinien.
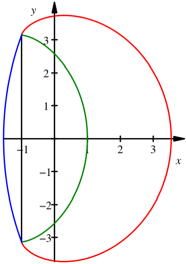
Beide Radlinien auf der
Zykloide
Numerisch ergibt sich:
![]()
So weit so gut. Die
Sache hat allerdings einen Haken. Die Zykloidenkrümmung
![]()
wird für ![]() beliebig groß,
das heißt, dass die Zykloide gegen die Enden zu beliebig stark gekrümmt ist und
sicher einmal stärker als der abrollende Kreis. Auf der linken Seite der
Zykloide kann also der abrollende Kreis die Zykloide nicht ganz ausfahren. Man
muss sich da von der mechanischen Vorstellung des Abrollens lösen.
beliebig groß,
das heißt, dass die Zykloide gegen die Enden zu beliebig stark gekrümmt ist und
sicher einmal stärker als der abrollende Kreis. Auf der linken Seite der
Zykloide kann also der abrollende Kreis die Zykloide nicht ganz ausfahren. Man
muss sich da von der mechanischen Vorstellung des Abrollens lösen.
5.2.2
Mehrere Bogen
Wir wählen ![]() , es gibt also m
Bogen. Die Abbildung zeigt den Fall
, es gibt also m
Bogen. Die Abbildung zeigt den Fall ![]() mit den Bogen
links und rechts.
mit den Bogen
links und rechts.
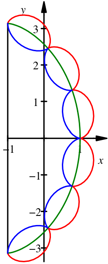
Sechs Bogen links und
rechts
Die einzelnen Bögen
links sind unterschiedlich lang:
Bogenlänge links [1] = 1.515961025
Bogenlänge links [2] = 1.592902016
Bogenlänge links [3] = 1.606040627
Bogenlänge links [4] = 1.606040627
Bogenlänge links [5] = 1.592902016
Bogenlänge links [6] = 1.515961025
Für die Gesamtlänge
erhalten wir:
Summe der Bogenlängen links =
9.429807335 = 59.2492269/(2*PI)
Für ![]() erhalten wir:
erhalten wir:
Summe der Bogenlängen links = 10.13635562 = 63.68860067/(2*PI)
Für ![]() ergibt sich:
ergibt sich:
Summe der Bogenlängen links =
10.1808667 = 63.96827206/(2*PI)
Vermutlich gilt auch
links:
![]()