Hans Walser, [20111231] / [20120102]

Zykloidenapproximation
Anregung: R. W., F.

1 Abrollen eines regelmäßigen n-Ecks

Wir rollen ein regelmäßiges n-Eck mit Umkreisradius 1 auf einer Geraden ab und verfolgen den Weg eines partikulären Eckpunktes. Beim Dreieck setzt sich dieser Weg aus zwei Kreisbogen zusammen, welche die Seitenlänge des Dreieckes als Radius haben (Abb. 1).

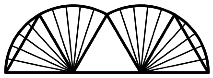
Abb. 1: Abrollen des Dreiecks

Beim Fünfeck haben wir vier Kreisbogen. Die Radien sind die Seiten- und Diagonalenlängen des Fünfeckes

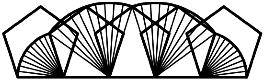
Abb. 2: Abrollen des Fünfecks

Beim Siebeneck (Abb. 3) haben wir sechs Bögen, deren Radien der Reihe nach die Längen der von einem Eckpunkt ausgehenden Seiten und Diagonalen sind („Diagonalenfächer“). Bei einem n-Eck haben wir entsprechend Bögen.

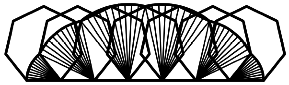
Abb. 3: Abrollen des Siebenecks

Für wachsendes n nähert sich die Bogenfigur der Zykloide an. Die Abbildung 4 zeigt die Situation für .

Abb. 4: Approximation der Zykloiden

2 Farbige Dreiecke

Zwischen den Sektoren sehen wir weiße Dreiecke, die wir in der Abbildung 5 rot färben. Zudem lassen wir die n-Ecke weg.

Abb. 5: Rote Dreiecke

Nun ersetzen wir auch noch die Kreissektoren durch je zwei gleichschenklige Dreiecke, eins gelb und das andere blau. Die Abbildung 6 illustriert den Fall . Der Kreisbogen wird also durch einen Polygonzug mit zwei Strecken ersetzt.

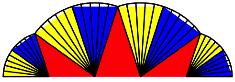
Abb. 6: Gelbe und blaue Dreiecke

Im folgenden lassen wir die Kreisbogen weg. Die Abbildung 7 illustriert die Fälle und . Wir sehen die Zykloide auch so. (Wir werden im Folgenden fast immer mit den Beispielen und illustrieren.)

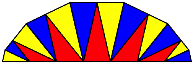
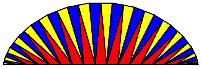
Abb. 7: Drei Farben

Nun lassen wir die gelben und blauen Dreiecke mal weg und klappen die übrig bleibenden roten Dreiecke zusammen wie ein Taschenmesser. Es entsteht das ursprüngliche n-Eck, unterteilt durch seine Diagonalen (Abb. 8).

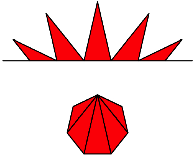
Abb. 8: Ein- und Ausklappen

Für entsteht der Einheitskreis.

Die gelben Dreiecke für sich genommen lassen sich auf einen Startpunkt zusammenschieben (Abb. 9).

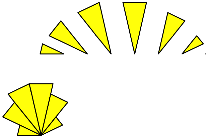
Abb. 9: Die gelben Dreiecke

Für entsteht der Einheitskreis. Analoges gilt für die blauen Dreiecke.

3 Flächeninhalt

Wenn wir die Dreiecke nach Farben sortieren (Ab. 10 für ), erhalten wir für drei Einheitskreise.

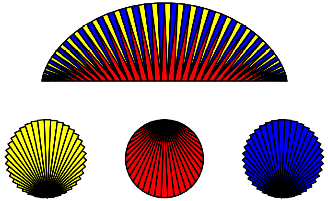
Abb. 10: Drei Einheitskreise

Somit hat die Fläche unter dem Zykloidenbogen den Inhalt , ein pro Farbe.

4 Bogenlänge

Nun entfernen wir die blauen Dreiecke und klappen die verbleibenden gelben und roten Dreiecke zusammen (Abb. 11).

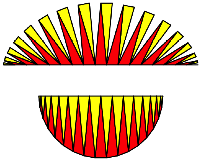
Abb. 11: Halbkreis

Es entsteht ein prächtiger Halbkreis. Dieser besteht aus zwei Farben, hat also den Flächeninhalt . Sein Durchmesser ist daher 4. Nun ist dieser Durchmesser genau die halbe Bogenlänge der Zykloide (es fehlen die blauen).

Somit hat der Zykloidenbogen die Länge 8. Dieses Resultat geht auf Christopher Wren (1658) zurück.

5 Die gelben Dreiecke allein

Nun entfernen wir im Halbkreis der Abbildung 11 die roten Dreiecke und klappen die gelben zusammen (Abb. 12). Die Scharniere sind jetzt an den oberen Ecken der gelben Dreiecke.

Abb. 12: Neue Zykloide

Wir sehen verschiedenes. Die obere Kontur ist eine verkleinerte Ausgabe der ursprünglichen Zykloide. Die Bogenlänge ist 4 (Durchmesser des Halbkreises der Abbildung 11). Somit ist die Zykloide längenmäßig halb so groß wie die ursprüngliche Zykloide. Der Flächeninhalt oberhalb der Spannsehne ist ein Viertel des Flächeninhaltes unter dem ursprünglichen Zykloidenbogen, also . Die Gesamtfläche der Figur ist aber (gelbe Farbe). Damit ist der Flächeninhalt unter der Wasserlinie , ein Viertel der Gesamtfläche. Weiter sehen wir, dass die Zykloide eine Evolvente ist von Kurven, die ihrerseits kongruente Zykloiden sind. Die Gesamtfigur hat daher den Umfang 8.

6 Gelbe und blaue Dreiecke

6.1 Scharniere oben

Wir klappen nun die gelben und blauen Dreiecke von oben her zusammen. Die Scharniere sind also an den oberen Ecken der Dreiecke (Abb. 13).

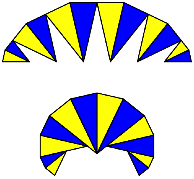
Abb. 13: Epizykloiden

Die obere Umrisskurve ist gleich lang wie die ursprüngliche Zykloide, hat also die Länge 8. Sie ist Evolvente der unteren Umrisskurve. Die untere Umrisskurve hat also die Länge 4 (zwei Mal die Fadenlänge 2).

Die Umrisskurven sind Epizykloiden, welche durch Abrollen eines halb so großen Kreises auf einem Grundkreis entstehen. Die obere Umrisskurve hat die Darstellung:

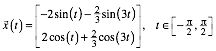
Die untere Umrisskurve har die Darstellung:

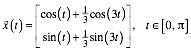
6.2 Fehlanzeige

Wir bündeln die gelben und blauen Dreiecke nun an den unteren Spitzen (Abb. 14 für und ).

Abb. 14: Was ist die Umrisskurve?

Der Autor vermutete zunächst, dass für die Kardioide (Herzkurve) entsteht. Das ist aber falsch. Die Abbildung 15 zeigt links „unsere“ Kurve (schwarz) und rechts zusätzlich die Kardioide (rot).

Abb. 15: Vergleich mit Kardioide

Der Unterschied besteht in folgendem:

Unsere Kurve hat die Parameterdarstellung:

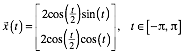
Der Flächeninhalt ist (zwei Farben).

Die Kardioide entsteht durch Abrollen eines Kreises auf einem anderen Kreis, wobei beide den gleichen Durchmesser a haben. In unserem Fall ist . Sie hat dann die Parameterdarstellung:

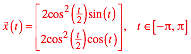
Das Quadrat mach den Unterschied. Der Flächeninhalt der Kardioide ist .

7 Doppelter Bausatz

Man kann ja auch unbescheiden sein, und zwei Bausätze kombinieren. Zunächst setzen wir mit den roten Dreiecken des einen Satzes das regelmäßige Vieleck zusammen. Anschließend setzen wir die roten Dreiecke des zweiten Satzes außen an gemäß Abbildung 16. Sie können sich selber einen Namen für dieses Insekt ausdenken.

Abb. 16: Zwei rote Bausätze

Nun haben wir gewaltige Lücken. Aber die gelben und blauen Dreiecke der beiden Sätze reichen zusammen gerade aus, diese Lücken aufzufüllen (Abb. 17).

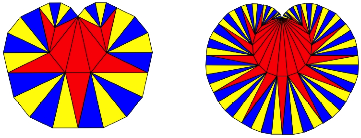
Abb. 17: Auffüllen der Lücken

Wir erhalten nun wirklich eine Kardioide. Diese hat den Umfang 16 (gelb und blau je doppelt) und den Flächeninhalt (drei Farben je doppelt). Die Fläche ist vier Mal so groß wie oben angegeben, weil wir nun auf dem Einheitskreis mit Durchmesser 2 abrollen.

8 Rote Dreiecke allein

8.1 Zickzack

Die roten Dreiecke entsprechen einer Zerlegung des regelmäßigen n-Ecks durch den Diagonalenfächer eines Eckpunkts (Abb. 8). Dieselben Dreiecke ergeben sich aber auch aus einer Zickzackzerlegung (Abb. 18). Wie viele Möglichkeiten gibt es überhaupt, die roten Dreiecke zum regelmäßigen Vieleck zusammenzusetzen?

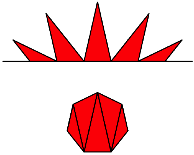
Abb. 18: Zickzack

Nun nehmen wir lediglich die Zicks (Spitze nach oben) und lassen die Zacks weg (Abb. 19). Das ist in etwa die halbe Miete.

Abb. 19: Nur Zicks

8.2 Tropfen

Wir denken uns nun die Zicks der Abbildung 19 an den unteren Ecken gelenkig verbunden und klappen zusammen wie ein Taschenmesser. Es entsteht eine tropfenförmige Figur (Abb. 20).

Abb. 20: Tropfen

Der untere Rand ist ein regelmäßiger Polygonzug, im Vergleich mit dem ursprünglichen n–Eck sind die Richtungsänderungen aber anderthalb Mal so groß ( statt ). Die „Krümmung“ ist also anderthalb Mal so groß. Für geht der Untere Rand also gegen einen Kreis mit dem Radius . Da der Umfang die Hälfte des ursprünglichen Kreisumfanges ausmacht, haben wir somit als unteren Rand einen . Wie sich der Rand dann zur Spitze fortsetzt, weiß ich nicht. Es ist kein Kreisbogen.

Mit den Zacks können wir einen Gegentropfen bauen (Abb. 21).

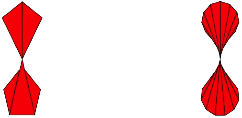
Abb. 21: Doppeltropfen

8.3 Kleeblatt

Nun fassen wir die Zicks oben an den Spitzen zusammen (Abb. 22).

Abb. 22: Gesammelte Zicks

Das gibt eine recht bescheidene Sache. Daher bündeln wir auch noch die Zacks, legen sie oben rechtwinklig an und verdoppeln die Figur mit einer Punktspiegelung (Abb. 23).

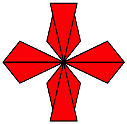
Abb. 23: Zicks in der Vertikalen und Zacks in der Horizontalen

Wir erhalten ein Kreuz, das sich für als Kleeblatt darstellt (Abb. 24 für ).

Abb. 24: Rotes Kleeblatt

Und zum Schluss nochmals eine Fehlanzeige: Die Randlinie, eine doppelte 8, ist keine Lemniskate. Die Abbildung 25 zeigt links die richtige Randlinie (schwarz) und rechts zusätzlich die Lemniskate (blau).

Abb. 25: Randkurve und Lemniskate

Die Lemniskate ist zu dick.

Die Randkurve hat die Parameterdarstellung:

Der Flächeninhalt ist insgesamt (zwei Mal rot), pro Blatt also .

Die gezeichnete Lemniskate hat die Parameterdarstellung:

Die Wurzel macht den Unterschied. Pro Blatt hat die Lemniskate den Flächeninhalt 2.

9 Hands on Geometry

9.1 Modell

Im Anhang findet sich ein Bastelbogen für und in zwei Größen. Dieser kann auf Karton aufgezogen und dann ausgeschnitten werden. Damit können wir spielen.

9.2 Virtuell

Mit DGS wird eine Vorlage konstruiert, die dann in ein Grafikprogramm übertragen wird. Dort wird die Bastelbogenfigur in die einzelnen Dreiecke aufgelöst, die dann virtuell auf dem Bildschirm bewegt werden können. Man braucht lediglich Translationen und (mehrfache) Drehungen um . Für viele Beispiele genügen Drehungen um . Da die Dreiecke paarweise spiegelbildlich sind, genügt ein „halber“ Bogen. Wir benötigen dann aber noch Spiegelungen.

Ebenso kann mit CAS gearbeitet werden. Die benötigten Eckpunkte der Dreiecke können in vielen Fällen (etwa Abb. 14. 23) in Polarkoordinaten einfach angegeben werden. Dann ist es auch einfach, daraus die Darstellung für den Grenzfall anzugeben. In anderen Beispielen (etwa Abb. 13, 20) müssen die Punkte rekursiv definiert werden. In diesen Fällen kann nicht direkt eine Darstellung für gefunden werden.

9.3 Im Kopf

Der Umgang mit Modellen oder virtuellen Modellen fördert die Fähigkeiten, sich die Figuren vorzustellen. Dann ist man unabhängig von der Realität und vom Computer.

Hands on Geometry findet im Kopf statt.

9.4 Der Grenzfall

Der Grenzübergang kann nur im Kopf vollzogen werden. Aus den diskreten Winkeln wird schreibtechnisch ein , aus den in der Programmierung (CAS) vorkommenden Winkeln wird dann einfach t. Häufig haben wir den Fall (da die Peripheriewinkel halb so groß sind wie die Zentriwinkel), woraus sich dann ergibt.

Anhang: Bastelbogen

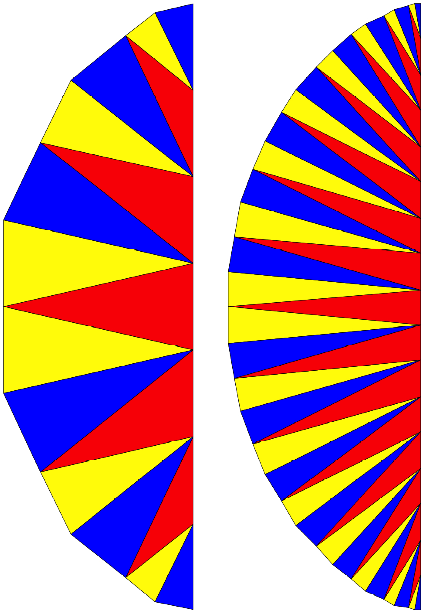
Bastelbogen für und , klein

Bastelbogen , linke Seite

Bastelbogen , rechte Seite

Bastelbogen , linke Seite

Bastelbogen , rechte Seite