Hans Walser, [20220124], [20220218]

Zylinder-Keil

1 Worum geht es?

Volumen eines „runden“ Körpers ohne die Kreiszahl π in der Formel.

Sture Rechenaufgabe mit verblüffendem Resultat.

2 Zwei Körper im Würfel

Einem Würfel wird einerseits eine Pyramide (Abb. 1a) und andererseits ein Zylinder-Keil (Abb. 1b) einbeschrieben. Der Keil ist aus einem Viertelzylinder herausgeschnitten.

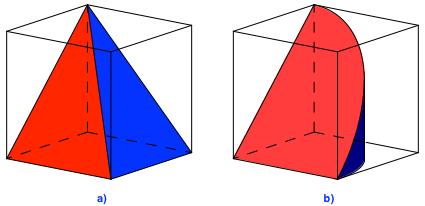
Abb. 1: Pyramide und Zylinder-Keil

Die Abbildung 2 zeigt den Zylinder-Keil von verschiedenen Seiten. Der gekrümmte Rand der schiefen Ebene ist ein ebener Ellipsenbogen (Viertel einer Ellipse), also keine Schraubenlinie. Die Steigung gegenüber dem Boden nimmt mit zunehmender Höhe ab.

Abb. 2: Zylinder-Keil

3 Problemstellung

Welcher der beiden Körper hat das größere Volumen?

4 Didaktischer Senf

Die Pyramide ist ein Klassiker. Im Unterricht wird gezeigt, dass drei solche Pyramiden lückenlos und überlappungsfrei in den Würfel passen. Das Volumen der Pyramide ist also ein Drittel des Würfelvolumens. Schön rational.

Der aus einem Viertel-Zylinder herausgeschnittene Keil hat eine runde Mantelfläche. Da ist zu befürchten, dass die irrationale Kreiszahl π hineinspielt.

5 Volumenberechnungen

Wir rechnen im Einheitswürfel.

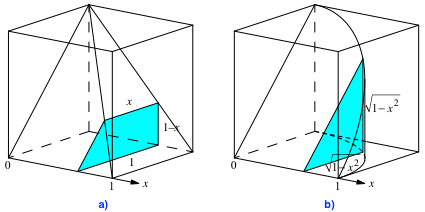
Abb. 3: Schnitte parallel zu den Seitenflächen

Wir schneiden die beiden Körper je mit einer zu den Seitenflächen des Würfels parallelen Ebene im Abstand x von der linken Seitenfläche (Abb. 3).

5.1 Pyramide

Bei der Pyramide ist die Schnittfigur ein Trapez mit der Grundkante 1, der Deckkante x und der Höhe 1 – x. Das Trapez hat den Flächeninhalt:

(1)

Daraus ergibt sich für das Pyramidenvolumen:

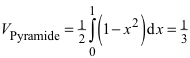(2)

5.2 Zylinder-Keil

Beim Zylinder-Keil ist die Schnittfigur ein rechtwinklig gleichschenkliges Dreieck. Es hat die Kathetenlänge:

(3)

Für den Flächeninhalt ergibt sich:

(4)

Das Trapez bei der Pyramide und das rechtwinklig gleichschenklige Dreieck beim Zylinder-Keil sind flächengleich. Damit ist alles klar.

Wir erhalten für das Volumen des Zylinder-Keils:

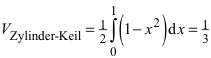(5)

Die beiden Körper haben dasselbe Volumen.

6 Oberflächen

Wenn wir schon am Rechnen sind, nun auch noch die beiden Oberflächen.

6.1 Pyramide

Die Oberfläche (inklusive Boden) der Pyramide besteht aus einem Einheitsquadrat, zwei rechtwinklig gleichschenkligen Dreiecken der Kathetenlänge 1 und zwei rechtwinkligen Dreiecken mit der einen Kathete 1 und der anderen Kathetenlänge gleich der Quadratwurzel aus 2.

Für die gesamte Oberfläche der Pyramide erhalten wir daher:

(6)

6.2 Zylinder-Keil

Die Mantelfläche des Zylinder-Keils lässt sich in die Ebene abwickeln (Abb. 4). Sie ist ein halber Sinusbogen und hat den Flächeninhalt 1. Erstaunlich, dass da die Kreiszahl π erneut fehlt.

Abb. 4: Mantelfläche

Allerdings ist der Boden des Zylinder-Keils ein Viertelkreis und die schräge Deckfläche eine Viertel-Ellipse mit den Halbachsen 1 und Quadratwurzel aus 2. Hier ist die Kreiszahl π unerlässlich. Für die gesamte Oberfläche erhalten wir:

(7)

Die Oberfläche des Zylinder-Keils ist etwas kleiner als jene der Pyramide.

Websites

Hans Walser: Rund ohne π

http://www.walser-h-m.ch/hans/Miniaturen/R/Rund_ohne_Pi/Rund_ohne_Pi.htm

Hans Walser: Zylinder-Keil

http://www.walser-h-m.ch/hans/Miniaturen/Z/Zylinder-Keil/Zylinder-Keil.html