Publication List
Last modified: December 17, 23
Articles
A158 2023 Brigitte Lutz-Westphal, Patrik Kolb und Hans
Walser: Werkstatt Mathematikunterricht. Aufgaben im Dialog III. Mitteilungen
der Deutschen Mathematiker-Vereinigung, 2023, 31, 4, S. 271-273.
A157 2023 Hans Walser: Invariante Flächensummen. In:
Andreas Filler · Anselm Lambert · Marie-Christine von
der Bank (Hrsg.) Freude an Geometrie –Zum Gedenken an Hans Schupp Vorträge auf
der 36. Herbsttagung des Arbeitskreises Geometrie in der Gesellschaft für Didaktik der Mathematik vom 10. bis 12. September 2021
in Saarbrücken. S. 237-248. Springer Spektrum. 2023.
ISBN 978-3-662-67393-5. ISBN 978-3-662-67394-2 (eBook).
https://link.springer.com/book/10.1007/978-3-662-67394-2
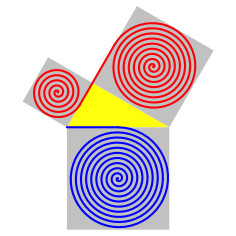
Einige geometrische Sätze, insbesondere der Satz des Pythagoras, werden unter
dem Aspekt der invarianten Flächensumme untersucht. Diese neue Sichtweise
ermöglicht ein ganzes Feld von Verallgemeinerungen und zugehörigen
Illustrationen.
A156 2023 Hans Walser: Rhombenfiguren. In: Frank Förster,
Torsten Fritzlar & Benjamin Rott (Hrsg): Probleme
sind zum Lösen da. Eine mathematisch-didaktische Festschrift zur Verabschiedung
in den Ruhestand von Prof. Dr. Frank Heinrich. WTM Verlag für
wissenschaftliche Texte und Medien, Münster 2023. ISBN
978-3-95987-182-2. S. 279-310.
https://www.wtm-verlag.de/festschriften-8/

Wir verwenden Rhomben als Bauteile für zusammengesetzte Figuren in der Ebene
und im Raum. Zunächst arbeiten wir mit Rhomben, die alle die gleichen Winkel
haben, die also zueinander ähnlich sind. Dies ermöglicht Verallgemeinerungen von
Sätzen der Elementargeometrie. Wir finden eine struktursymmetrische Schließungsfigur
und erhalten eine neue Sicht auf den Satz des Pythagoras. Anschließend
verwenden wir Rhomben, die alle die gleiche Seitenlänge haben. Damit schaffen
wir den Übergang von der Ebene in den Raum. Wir konstruieren einen
Rhombenkörper, der die Kosinusspindel approximiert.
A155 2023 Hans Walser: Vielecke einpacken. MU. Der
Mathematik-Unterricht. 69, Heft 3, August 2023. S. 10-17.
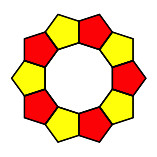
Welche regelmäßigen Vielecke können von regelmäßigen Vielecken eingepackt
werden? Die Frage der Lösbarkeit wird mit Winkelberechnungen angegangen. Eine
Verallgemeinerung führt zu regelmäßigen Stern-Figuren.
A154 2023 Hans Walser: Quadrate und Schnittpunkte. MU.
Der Mathematik-Unterricht. 69, Heft 3, August 2023. S. 4-9.
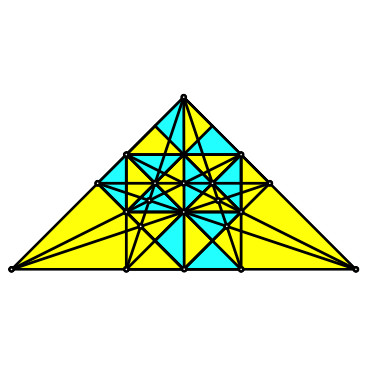
Ausgehend von einem speziellen Schnittpunkt in der
Beweisfigur des Euklid zum Satz von Pythagoras finden wir zusätzliche Quadrate
und spezielle Schnittpunkte. Für die Beweise arbeiten wie hauptsächlich mit der
Ähnlichkeit.
A153 2022 Hans Walser: Invariante Flächensummen. MU.
Der Mathematik-Unterricht. 68, Heft 4, Oktober 2022. S. 45-56.
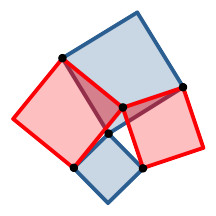
Ein Perspektivenwechsel beim Satz des Pythagoras führt fast zwangsläufig zu
vielen Verallgemeinerungen. Diese lassen sich entweder von Fall zu Fall durch
oft mühsame trigonometrische Rechnungen nachweisen oder dann recht einfach im
großen Überblick durch eine fast physikalische Schwerpunktüberlegung. Im
Hintergrund spielen Symmetrien, oft Drehsymmetrien, eine zentrale Rolle. Mit
heute im Schulunterricht gängiger dynamischer Geometrie-Software lassen sich
Animationen bauen.
A152 2022 Hans Walser: Magic Symmetry. Mathematics and
Its Connections to the Arts and Sciences (MACAS). 15 Years of Interdisciplinary
Mathematics Education. Editors: Claus Michelsen, Astrid Beckmann, Viktor Freiman, Uffe Thomas Jankvist, Annie Savard. P. 467-485. Springer Nature, 2022.
ISBN 978-3-031-10517-3. doi.org/10.1007/978-3-031-10518-0.
A151 2022 Jo Niemeyer und Hans Walser: Trisection of
an Angle. Bridges Aalto 2022. Mathematics / Art / Music / Architecture /
Culture. Conference Proceedings. P. 407-408. ISBN 978-1-938664-42-7. ISSN 1099-6702
Dividing an angle into thirds is one of the three classic problems that cannot
be solved with ruler and compass, along with doubling the cube and squaring the
circle. We discuss a very simple fit-in solution using squares.
A150 2022 Hans
Walser: Winkelschwerpunkte. IBDG. Informationsblätter der Geometrie. Heft
1/2022. Jahrgang 41. S. 35-36.
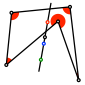
Mit den Winkeln im und am Dreieck werden drei spezielle Punkte definiert. Diese
liegen in einem invarianten Teilverhältnis auf einer Geraden. Auch der
Schwerpunkt des Dreiecks liegt auf dieser Geraden. Die Definitionen geben
Anlass, über die Konstruierbarkeit mit Zirkel und Lineal nachzudenken.
A149 2022 Hans Walser: Quadrate in Rhomben. MI, Mathematikinformation Nr.
76, 15. Januar 2022. ISSN 1612-9156. 5-15.

In einen Rhombus werden zwei verschieden positionierte Quadrate eingebaut. Wir
untersuchen das Flächenverhältnis dieser beiden Quadrate in Abhängigkeit von
der Form des Rhombus. Die Gleichheit der beiden Quadrate führt zum DIN-Format
und einer speziellen Parkettierung. Bei einem rationalen Diagonalenverhältnis
des Rhombus kann das Flächenverhältnis der beiden Quadrate in einem gemeinsamen
Raster ausgezählt werden.
A148 2021 Hans
Walser: Hyperbolische Kepler-Sterne. IBDG. Informationsblätter der
Geometrie. Heft 2/2021. Jahrgang 40. S. 30-31.
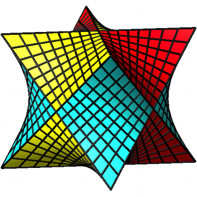
Es werden zwei verschiedene Möglichkeiten vorgestellt, einem Kepler-Stern
hyperbolische Flächen zu applizieren.
A147 2021 Hans Walser: Spiralen in Rechtecken. MI, Mathematikinformation
Nr. 75, 15. September 2021. ISSN 1612-9156. 3-15.
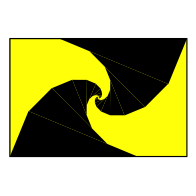
In Rechtecke werden eckige logarithmische Spiralen eingebaut. Dabei wird mit
rechtwinkligen Dreiecken gearbeitet. Wir erhalten auch einen geometrischen
Zugang zu pythagoreischen Dreiecken.
A146 2021 Hans Walser: Spiel mit Quadraten. MU, Der Mathematikunterricht.
Jahrgang 67. Heft 3-2021. S. 17-27. ISSN 0025-5807.
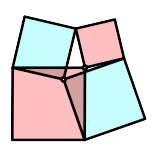
Wir arbeiten mit zwei Quadraten, welche an einer Ecke gelenkig verbunden sind.
Einfügen weiterer Geraden oder Quadrate führt auf spezielle Schnittpunkte von
drei Geraden und auf invariante Flächensummen. Folgende Geometrie-Kompetenzen
der Sekundarstufe 1 werden aktiviert: Ähnlichkeit und Strahlensatz, Satz des
Pythagoras, Peripheriewinkel am Kreis, Kongruenz- und Bewegungsgeometrie,
Zerlegungsgleichheit, Rotationssymmetrie, rechnerische Beweise und dynamische
Geometrie-Software.
A145 2021 Hans
Walser: Geometrie mit dynamischer Geometrie-Software. In: Eva Vasarhelyi & Johann Sjuts
(Hrsg.): Theoretische und empirische Analysen zum geometrischen Denken.
WTM-Verlag für wissenschaftliche Texte und Medien, Münster. S. 405-418. Print:
ISBN 978-3-95987-199-0
Ebook: ISBN 978-3-95987-200-3
DOI: https://doi.org/10.37626/GA9783959872003.0
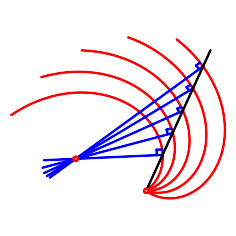
Die dynamische Geometrie Software (DGS) ist seit langem im Schulunterricht
etabliert und im Lehrplan verankert. Nach meinen Erfahrungen wird allerdings
dynamische Geometrie Software im schulischen Bereich sehr oft nur als
Zeicheninstrument gehandhabt. Damit wird das eigentliche Potential dieser
Software nicht ausgenützt. Für geometrische Fragen wird nach wie vor mit Zirkel
und Geodreieck gearbeitet. Dabei stellt sich die entwicklungspsychologische
Frage, ob man die tradierten Methoden beherrschen müsse, um die aktuellen
Methoden nutzbringend anwenden zu können. Es gibt aber interessante Beispiele,
welche zunächst spezifische technische Fragen um die Handhabung der dynamischen
Geometrie Software aufwerfen. Diese Fragen tangieren auch das tradierte Bild
der Geometrie. Es werden exemplarisch einige Fälle dazu vorgestellt (Inkreis,
archimedische Spiralen, Zykloide). Dabei kommen wir zu Fragen der
Arbeitsökonomie, der logischen Schlüssigkeit und der strukturellen Symmetrie
A144 2020 Hans Walser: Aufwickeln und Abwickeln. In: Andreas Filler und Anselm Lambert (Hrsg.): Geometrie als Quelle von
Bildung: Anwenden, Strukturieren, Problemlösen. Vorträge auf der 36.
Herbsttagung des Arbeitskreises Geometrie in der Gesellschaft für Didaktik der
Mathematik vom 13. bis 15. September 2019 in Saarbrücken. S. 41-60. ISBN
978-3-88120-616-7.
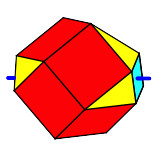
Unter dem Aspekt „Aufwickeln und Abwickeln“ finden sich in der Mathematik und
insbesondere in der ebenen und räumlichen Geometrie, aber auch in der Technik,
verschiedene, zum teil lose zusammenhängende Figuren,
Methoden und Prozesse, Bilder und Kurven.
A143 2020 Hans
Walser: Ortsbogen. IBDG. Informationsblätter der Geometrie. Heft 2/2020.
Jahrgang 39. S. 55-56.
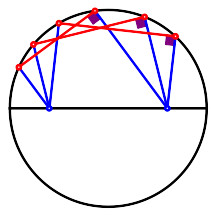
Der Umfangwinkelsatz mit dem Ortsbogen lässt sich in einen größeren
Zusammenhang einbetten.
A142 2020 Hans
Walser: Falsche Perspektive. IBDG. Informationsblätter der Geometrie. Heft
2/2020. Jahrgang 39. S. 27-30.
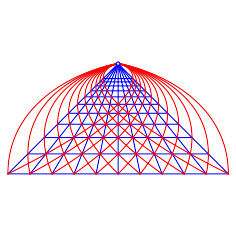
Diskussion der Sonne am Wolfgangsee
A141 2020 Kinga Szücs,
Hartmut Müller-Sommer, Hans Walser, Jörg Meyer: Winkeldreiteilung mit einer
Hyperbel. MU, Der Mathematikunterricht. Jahrgang 66. Heft 1-2020. S. 32-36.
ISSN 0025-5807.
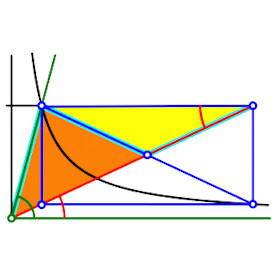
János Bolyai, der Vater
einer nichteuklidischen Geometrie, hat ein Verfahren entwickelt, mit Hilfe der
zu xy = 1 gehörigen Hyperbel Winkel zu dritteln.
A140 2020
Hans Walser: Le théorème d’Eddy. VSMP Bulletin. Janvier 2020, No 142, p.
30-32.
A139 2019 Hans Walser: Satz des Pythagoras im Raum. ml mathematik lehren 216 | 2019. S. 44-46. ISSN 0175-2235.
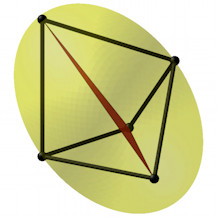
Wir schneiden von einem Würfel oder einem Quader eine Ecke ab. Das
abgeschnittene Stück ist ein unregelmäßiges Tetraeder. Drei Seitenflächen des
Tetraeders sind rechtwinklige Dreiecke, die vierte ein spitzwinkliges Dreieck.
Nun ist die Summe der Quadrate der Flächeninhalte der drei rechtwinkligen
Seitendreiecke gleich groß wie das Quadrat des Flächeninhaltes des
spitzwinkligen Seitendreiecks. Durch das Quadrieren der Flächeninhalte entstehen
Gebilde im vierdimensionalen Raum.
A138 2019 Hans Walser: Perspektivenwechsel. MI,
Mathematikinformation Nr. 71, 15. September 2019. ISSN 1612-9156. 3-11.
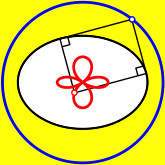
Orthoptische und isoptische
Kurven an Kegelschnitte.
A137 2019 Hans Walser: Der Satz von Eddy. VSMP Bulletin. September 2019, No
141, S. 14-16.
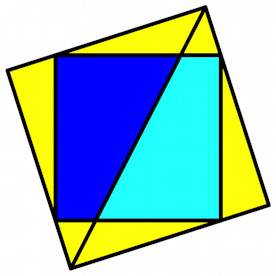
Ein elementargeometrischer Satz von Eddy führt auf eine
neue Sicht des Satzes von Pythagoras und eine Invarianz von
Flächenquadratsummen.
A136 2019 Hans Walser: Umkehrung. In: Andreas Filler
und Anselm Lambert (Hrsg.): Geometriedidaktik zwischen Geometrie und Didaktik.
Vorträge auf der 35. Herbsttagung des Arbeitskreises Geometrie in der
Gesellschaft für Didaktik der Mathematik vom 14. Bis 16. September 2018 in
Saarbrücken. S. 39-50.

Die Umkehrung der Sichtweise, ein Perspektivenwechsel also, führt zu neuen
Einsichten. Exemplarisch wird dies an der Umkehrung einer klassischen
Schulaufgabe der Sekundarstufe 2 gezeigt. Wir kommen zu einer Verallgemeinerung
der Begriffe „Thaleskreis“ und „Ortsbogen“.
A135 2019 Hans
Walser: Halbe Würfel. IBDG, Informationsblätter der Geometrie. Heft 2/2018,
Jahrgang 37. S. 37-42.
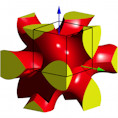
Ein Würfel kann nicht mit Zirkel und Lineal in einen volumenmäßig halb so
großen Würfel verwandelt werden. Hingegen gibt es eine Vielzahl von einfach zu
konstruierenden Figuren, welche das Würfelvolumen halbieren. Dabei spielen
Symmetrieüberlegungen eine wichtige Rolle. Mit diesen Figuren kann der Raum
lückenlos und überlappungsfrei aufgefüllt werden. Dabei zeigt sich der
Unterschied zwischen dem statischen „Passen“ und dem kinematischen „Einpassen“.
Die Überlegungen spielen in den Dimensionen zwei, drei und vier.
A134 2019 Hans Walser: IMO, Parität, Gleichdick und Archimedische Spirale. .
VSMP Bulletin, Januar 2019, Ausgabe 139, S. 46-47.
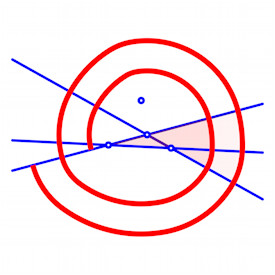
Eine kleine Erweiterung einer IMO-Aufgabe führt zu einem Paritätsproblem, zu
Kurven mit konstantem Durchmesser und zu einer Art archimedischer Spiralen.
A133 2018
Hans Walser: Semi-regular figures
between beauty and regularity. In: MATHEMATICS AS A BRIDGE BETWEEN THE
DISCIPLINES PROCEEDINGS OF MACAS – 2017 SYMPOSIUM HELD AT DANISH SCHOOL OF EDUCATION,
AARHUS UNIVERSITY, COPENHAGEN 27-29 JUNI, 2017. EDITED BY Claus Michelsen,
Astrid Beckmann, Viktor Freiman, and Uffe Thomas Jankvist. © 2018 LSUL, University of
Southern Denmark. ISBN
978-87-92321-27-5. 29-38.

A132 2018 Hans Walser: Rechtwinkliges Dreieck und Binomialverteilung. In Fachgruppe Didaktik der Mathematik der Universität Paderborn (Hrsg.) Beiträge zum Mathematikunterricht 2018 (S. 1907 - 1910). Münster: WTM-Verlag.
A131 2018 Hans Walser: Entdeckungen an einem halbregulären Fünfeck. In Fachgruppe Didaktik der Mathematik der Universität Paderborn (Hrsg.) Beiträge zum Mathematikunterricht 2018 (S. 1903 - 1906). Münster: WTM-Verlag.
A130 2018 Hans Walser: Magische Symmetrie. MI, Mathematikinformation
Nr. 69, 15. September 2018. ISSN 1612-9156. 25-33.
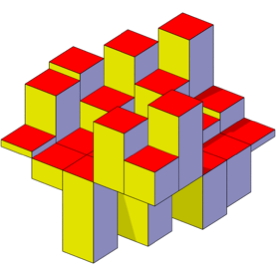
Bei der Analyse magischer Quadrate ungerader Seitenlänge treten verschiedene
Symmetrien auf. Umgekehrt ist für die Konstruktion magischer Quadrate ein
symmetrisches modulo-Rechnen problemadäquat. Ebenso brauchen wir ein
angepasstes symmetrisches Positionssystem.
A129 2018 Hans Walser: Bandornamente als
Scherenschnitte. Mathematik. Unterricht. Aufgaben. Materialien. 5 bis 10.
Papierkram. Verstehen mit und durch Papier. Materialpaket. 44. Bestell-Nr.
14644. 3. Quartal I 2018. 7.
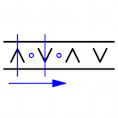
Arbeitsmaterial zu A128.
A128 2018 Hans Walser: Bandornamente aus Papier. Verschiedene Symmetrien
durch Scherenschnitte herstellen. Mathematik. Unterricht. Aufgaben.
Materialien. 5 bis 10. Papierkram. Verstehen mit und durch Papier. Materialien.
44. Bestell-Nr. 13844. 3. Quartal I 2018. 14-17.
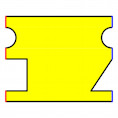
Bandornamente sind ein Paradebeispiel für Symmetrien und laden ein zu eigenen
Entdeckungen im Unterricht.
A127 2018 Hans Walser: Klassifikation der Symmetriegruppen der
Flächenornamente als Werkzeug. In: Andreas Filler,
Anselm Lambert (Hrsg.), Geometrie mit Tiefe. Vorträge auf der 34. Herbsttagung
des Arbeitskreises Geometrie in der Gesellschaft für Didaktik der Mathematik
vom 8. bis 10. September 2017. Hildesheim: Franzbecker 2018. 75-90. ISBN
978-3-88120-612-9.
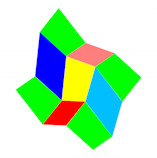
Die Klassifikation der Symmetriegruppen der Flächenornamente wird als
Hilfsmittel für den Beweis eines Theorems aus der Elementargeometrie verwendet.
Die Idee dabei ist, ein lokales Phänomen in eine Übersichtsdarstellung
einzubinden und von daher zu verstehen.
A126 2018 Hans Walser: Die Acht in der Kugel. MU, Der Mathematikunterricht.
Jahrgang 64. Heft 4-2018. S. 50-55.
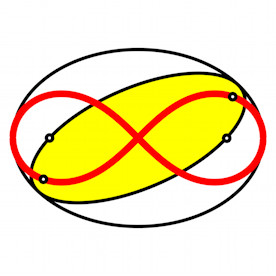
In einem Schrägbild der Erdkugel entdecken wir merkwürdige Eigenschaften der
Meridiane und Breitenkreise. Insbesondere finden wir auch die Lemniskate von
Bernoulli.
A125 2018 Hans
Walser: Schrägkanten-Modelle. IBDG, Informationsblätter der Geometrie,
Fachverband Geometrie. Heft 1/2018, Jahrgang 37, S. 26-31.

Aus einem einzigen Streifen können wir mit geeigneten Faltlinien Modelle bauen,
deren Ecken auf Ecken der platonischen Körper liegen. Die Modelle halten in der
Regel ohne Bindemittel und sind leicht wieder zerlegbar. Die Methode erlaubt
auch eine Faltkonstruktion des regelmäßigen Siebenecks.
A124 2018 Hans Walser: Zahnräder im Zeigerwerk. ml mathematik lehren 208 | 2018. S. 46-47.
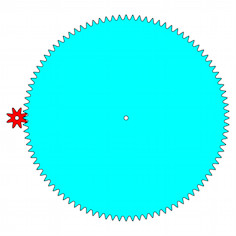
Zahnräder sind für die
passende Altersstufe (4. – 8. Klasse) geeignet, Fragen zu Verhältnissen ganzer
Zahlen, also Fragen rationaler Zahlen, implizit anzugehen. Am Beispiel einer
mechanischen Zeigeruhr wird die Irrationalität der Quadratwurzel aus 12
aufgezeigt.
A123 2018 Hans Walser: DIN A4 und US
Letter. ml mathematik lehren 208 | 2018. S.
34-35.
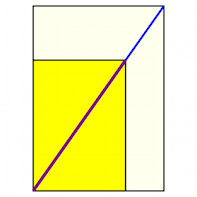
Die beiden gängigen Papierformate DIN A4 und US Letter
unterscheiden sich nicht nur (geringfügig) in den Ausmaßen, sondern auch und
vor allem im zugrundeliegenden geometrisch-mathematischen Konzept. Das US Letter Format hat ein rationales Seitenverhältnis, das
DIN A4 Format hingegen ist für Schülerinnen und Schüler was wohl erste Beispiel
eines irrationalen Verhältnisses. Dies kann mit verschiedenen Falt-Prozessen
aufgezeigt werden.
A122 2018 Hans Walser: Halbregelmäßiges Fünfeck. MU,
Der Mathematikunterricht. Jahrgang 64. Heft 2-2018. S. 38-46.

Wir arbeiten mit einer einzigen Figur, einer halbregelmäßigen Modifikation des
regelmäßigen Fünfeckes.
A121 2018 Hans Walser: Falsche Perspektive. MNU Journal – Ausgabe 2.2018.
S. 87-89.

Es werden zwei Testverfahren zur Erkennung von falschen Zentralperspektiven
besprochen.
A120 2017 Hans
Walser: Der Teufel sitzt im Detail. IBDG Informationsblätter der Geometrie.
Heft 2/2017. Jahrgang 36. S. 15-16.
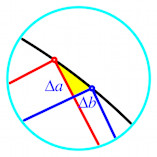
Diskussion von Beweisen zum Satz von Pythagoras.
A119 2017 Hans Walser: Würfel auf Ecke. mathematik
lehren 205 | 2017, 46-47.

Kann ein Würfel auf einer Ecke stehen? Oder anders
gefragt: Ist das Foto echt?
A118 2017 Hans Walser: Viererpuzzle. Aufgabenstellung: AZ/AN Magazin, Nummer 255, 4. Nov. 2017, letzte Seite. Lösung: AZ/AN Magazin, Nummer 261, 11. Nov. 2017, letzte Seite.
A117 2017 Hans Walser: Rechtwinklige Dreiecke ... . Ideenkiste. mathematik lehren 204 | 2017, 51.
A116 2017 Hans Walser: Dreiecksunterteilung und Binomialverteilung – In: Fachnewsletter mathematik lehren vom 18.9.2017
A115 2017 Hans Walser: Das erste Wachstumsmodell. In: Füglister, Kurt M. / Hicklin, Martin / Mäser, Pascal (Hg.): natura obscura. 200 Naturforschende — 200 Naturphänomene — 200 Jahre Naturforschende Gesellschaft in Basel. Basel: Schwabe 2017. ISBN 978-3-7965-3686-1. S. 210.
A114 2017 Heinz Klaus Strick und Hans Walser: Parabeln, Primzahlen und
Geradenfächer. mathematik lehren 201 | 2017, 42-44.
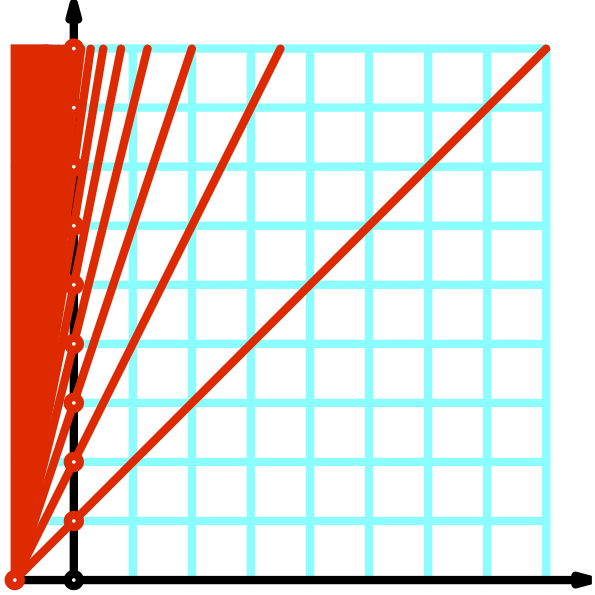
A113 2017 Hans Walser: Reuleaux-Zweiecke.
In: Andreas Filler, Anselm Lambert (Hrsg.), Von Phänomenen
zu Begriffen und Strukturen. Konkrete Lernsituationen für den Geometrieunterricht.
Vorträge auf der 32. Herbsttagung des Arbeitskreises Geometrie in der
Gesellschaft für Didaktik der Mathematik vom 11. bis 13. September 2015 und auf
der 33. Herbsttagung vom 09. bis 11. September 2016 in Saarbrücken. Hildesheim:
Franzbecker 2017. 165-176. ISBN 978-3-88120-610-5.

Analog zum Reuleaux-Dreieck,
das sich in verschiedenen Positionen ins immer gleiche Quadrat einpassen lässt,
gibt es Reuleaux-Zweiecke, die sich in ein
gleichseitiges Dreieck einpassen lassen. Es werden zwei Beispiele vorgestellt
sowie verschiedene Beweistechniken diskutiert: Rechnung, Einbinden in einen
übergeordneten Zusammenhang, Kinematik. Ein wichtiger Aspekt ist die
Beschreibung von Kurven in verschiedenen zueinander bewegten Referenzsystemen.
Schließlich wird eine Verallgemeinerung auf Reuleaux-Vierecke
besprochen.
A112 2017 Hans Walser: Ein namenloses Phänomen. In:
Andreas Filler, Anselm Lambert (Hrsg.), Von Phänomenen
zu Begriffen und Strukturen. Konkrete Lernsituationen für den
Geometrieunterricht. Vorträge auf der 32. Herbsttagung des Arbeitskreises Geometrie
in der Gesellschaft für Didaktik der Mathematik vom 11. bis 13. September 2015
und auf der 33. Herbsttagung vom 09. bis 11. September 2016 in Saarbrücken.
Hildesheim: Franzbecker 2017. 87-100. ISBN 978-3-88120-610-5.
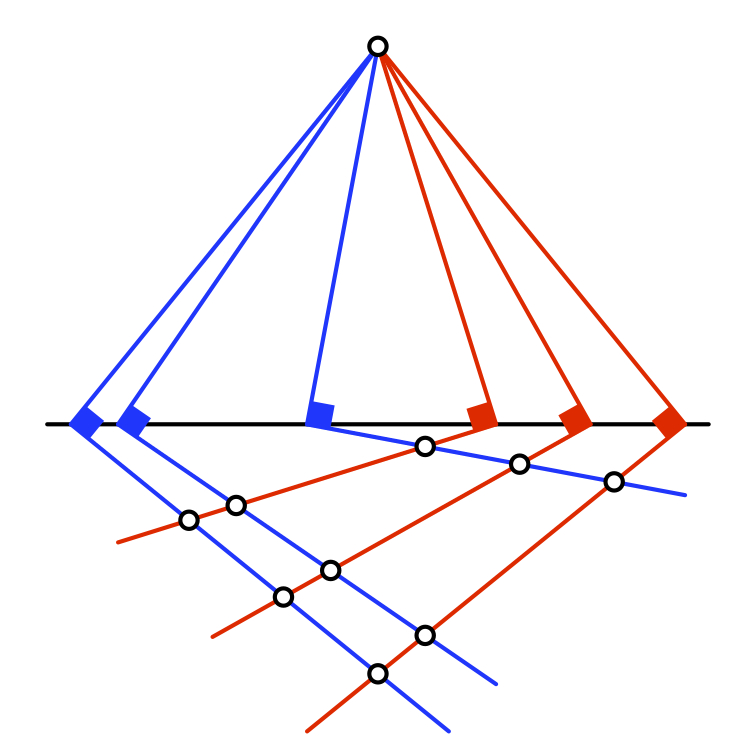
Ein Faltspiel und ein Spiel mit rechten Winkelhaken führen beide zu einem
symmetrischen Phänomen, welches im Lehrplan nicht kodifiziert ist. Der
(asymmetrische) Strahlensatz erweist sich als Grenzfall. Die Überlegungen
wurden angeregt durch einen didaktischen Fehler in einem Arbeitsblatt für das
achte Schuljahr.
A111 2017 Renato Pandi und Hans Walser: Reuleaux-Zweiecke. MNU Journal. Der mathematische und naturwissenschaftliche
Unterricht 70/4, 255-258. ISSN 0025-5866.

Analog zum Reuleaux-Dreieck, das sich in verschiedenen
Positionen ins immer gleiche Quadrat einpassen lässt, gibt es zwei Reuleaux-Zweiecke,
die sich in jeder Lage in ein gleichseitiges Dreieck einpassen lassen. Der Reiz
der Thematik liegt in der kinematischen Geometrie, also der Geometrie relativ
zueinander bewegter Figuren. Dies lässt sich mit realen Modellen sowie mit
Modellierungen in DGS zeigen.
A110 2017 Hans Walser: Wie viele Teiler hat die Zahl? ml mathematik lehren 200 | 2017, 50-51.
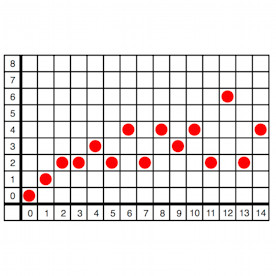
Vorgestellt wird eine einfache
Aktivität, mit der sich die Anzahl der Teiler von natürlichen Zahlen durch ein
schrittweises Verschieben von Knöpfen in einer Tabelle bestimmen lassen. Die
immer gleiche und monotone Formulierung der Schritte zeigt, dass ein
Algorithmus abgearbeitet wird. Die Schülerinnen und Schüler können bei der
Auswertung mehrere interessante Feststellungen machen. So kennzeichnen etwa
Knöpfe in der Reihe drei die Quadrate der Primzahlen.
A109 2016 Hans Walser: Spielereien im DIN-Format. MU,
Der Mathematikunterricht. Jahrgang 62. Heft 5-2016. S. 3-13.
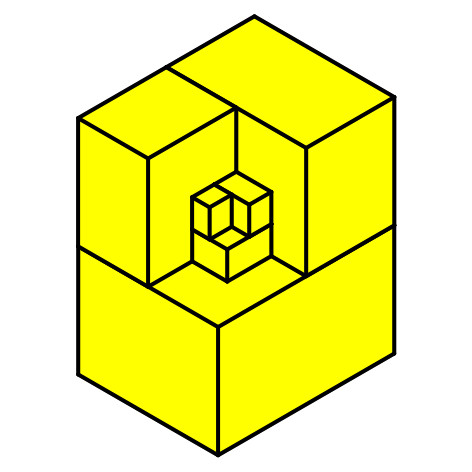
Das DIN A4-Papier ist Basis verschiedener mathematischer und insbesondere
geometrischer Aktivitäten: Falten, Zerlegen, Abschneiden und Hinzufügen,
Anordnen, Vergleichen und gelegentlich Rechnen. Wir kommen propädeutisch zu
Spiralen und Grenzprozessen und studieren Symmetrien in der Ebene und im Raum.
Es gibt Analogien zu anderen Figuren mit der DIN-Zerlegungseigenschaft, und wir
können in höhere Dimensionen verallgemeinern. Wird von einem DIN A4-Papier ein
Quadrat als Origami-Papier abgeschnitten, bleibt als „Abfall“ das so genannte
Silberne Rechteck übrig, das eng mit dem regelmäßigen Achteck verknüpft ist.
A108 2016 Renato Pandi und Hans Walser:
Kreisfiguren im Rhombus. MI, Mathematikinformation Nr. 65. S. 5-13.
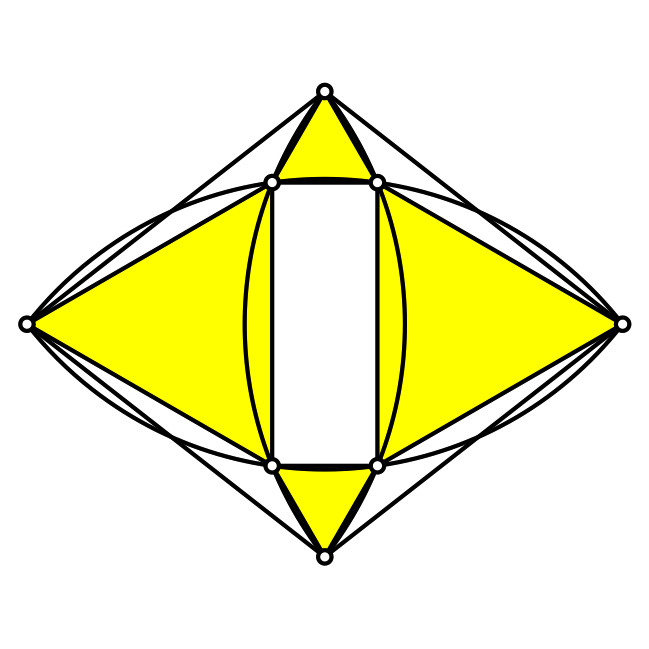
Im Rhombus finden wir durch Einzeichnen von Kreisbogen-Zweiecken neue
Zusammenhänge. Wir treffen auf gleichseitige Dreiecke, Winkelbeziehungen,
Invarianten, Delta-Kurven, Schnittpunkte und kinematische Prozesse. Ebenso
finden wir Zusammenhänge zu Architektur, Grafik und Süßigkeiten.
A107 2016 Hans Walser: Sehnenvieleck. VSMP Bulletin, September 2016, No 132, S.
29-31.

Konstruktionen mit MINT und Papier für das Sehnenvieleck.
A106 2016 Hans Walser: Winkeleisen. MNU Journal. Der mathematische und
naturwissenschaftliche Unterricht, 69/3, 158-160. ISSN 0025-5866.
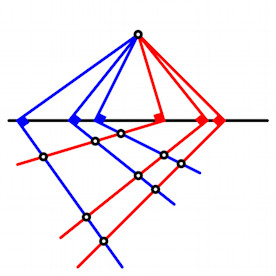
Die übliche Strahlensatzfigur ist begrifflich asymmetrisch. Wir haben
einerseits eine Schar von parallelen Geraden und andererseits eine Schar von
kopunktalen Geraden. Mit rechten Winkeln können wir aber eine begrifflich
symmetrische Figur mit gleichen Teilverhältnissen konstruieren. Die
Strahlensatzfigur ergibt sich daraus als Sonderfall mit einem Grenzübergang.
A105 2016 Hans Walser: Puzzles and Dissections. In Astrid Beckmann, Viktor Freiman, Claus
Michelsen: Proceedings of
MACAS–2015. Hildesheim: Franzbecker. ISBN 978-3-88120-760-7. p 124-132.

A104 2016 Hans Walser: Alternative Konstruktionen im Dreieck. Die Wurzel.
Zeitschrift für Mathematik. März/April 2016. S. 79-81.

A103 2016 Hans Walser: Vom Strahlensatz zum Strahlensatz – Motive und Phänomeine. In F. Caluori, H. Linneweber-Lammerskitten & C. Streit (Hrsg.), Beiträge zum Mathematikunterricht 2015. Münster: WTM-Verlag, S. 976-979.
A102 2016 Hans Walser: Siebenbannstein. In F. Caluori,
H. Linneweber-Lammerskitten & C. Streit (Hrsg.),
Beiträge zum Mathematikunterricht 2015. Münster: WTM-Verlag, S. 972-975.

A101 2016 Hans Walser: Das DIN-Format. Workshop. In F. Caluori,
H. Linneweber-Lammerskitten & C. Streit (Hrsg.),
Beiträge zum Mathematikunterricht 2015. Münster: WTM-Verlag, S. 968-971.

A100 2016 Jean Pedersen und Hans Walser: Pascal, Fibonacci and geometry. Elem.
Math. 71 (2016), 1-6.
A99 2015 Hans Walser: Vielecke aus Streifen. Der
Falter // Magazin. Origami Deutschland e. V., 64, Oktober 2015, 9-12

A98 2015 Hans Walser: DIN-Format und Raum. In: Andreas
Filler, Anselm Lambert (Hrsg.): Geometrie zwischen
Grundbegriffen und Grundvorstellungen. Raumgeometrie. Vorträge auf der 31.
Herbsttagung des Arbeitskreises Geometrie in der Gesellschaft für Didaktik der
Mathematik vom 12. Bis 14. September 2014 in Saarbrücken. Hildesheim:
Franzbecker. S. 105-119.
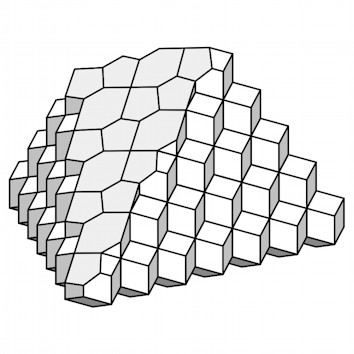
Ausgehend von didaktischen und erkenntnistheoretischen
Problemen der Raumgeometrie werden zunächst einige Modelle von Polyedern
vorgestellt, welche aus Papier oder Karton im DIN-Format hergestellt werden
können. Anschließend wird die Grundidee des DIN-Formates auf andere Figuren
übertragen, wobei wiederum der Raum eine wichtige Rolle spielt.
A97 2015 Hans Walser: Dreieck und Quader. Monoid 122. S. 4-5.
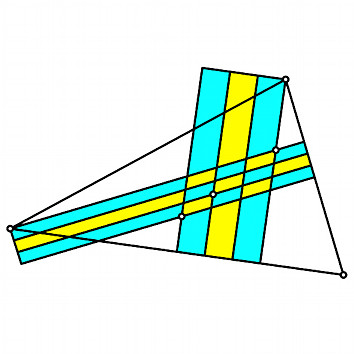
In einem Dreieck ABC zeichnen wir den
Umkreismittelpunkt U. Dann ergänzen
wir die drei Verbindungsstrecken vom Umkreismittelpunkt U zu den Ecken A, B, C
zum Bild eines Quaders. Die dem Punkt U
gegenüberliegende Ecke des Quaderbildes bezeichnen wir mit V. Welche Bedeutung hat der Punkt V für das Dreieck ABC?
A96 2015 Emese Vargyas und
Hans Walser: Verallgemeinerung des Satzes von Viviani.
MI, Mathematikinformation Nr. 63, 15. September 2015. ISSN 1612-9156. S. 3-10.
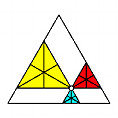
Der Satz von Viviani besagt, dass in einem gleichseitigen
Dreieck die Summe der Abstände von einem beliebigen Punkt im Innern des
Dreieckes unabhängig von der Lage des Punktes ist. Wir haben also eine
Invariante. Der Invariantenbegriff ist in der
Mathematik zentral, viele Sätze der Mathematik lassen sich mit Hilfe von
Invarianten formulieren und verstehen. Für die Beweise kommen verschiedene
Lösungswege zur Sprache, die je einen eigenen Aspekt der Mathematik beleuchten.
Der Satz von Viviani
kann in verschiedener Hinsicht verallgemeinert werden.
A95 2015
Hans Walser: Vieleck-Knoten.
MNU. Der mathematische und naturwissenschaftliche
Unterricht 68/4 (15. 7. 2015), S. 224-227. ISSN 0025-5866.

Die Konstruktion des regelmäßigen Fünfeckes als Papierstreifen-Knoten wird
zunächst auf das regelmäßige Siebeneck und weiter auf beliebige regelmäßige
Vielecke verallgemeinert. Dabei treffen wir auf ein
gerade-ungerade-Paritätsproblem, auf topologische Fragen und
Teilbarkeitsprobleme.
A94 2015 Hans Walser: Maßstab 1:1 – Geometrie für Geomatiker (2015). In: Ludwig, Mathias und Filler, Andreas und Lambert, Anselm: Geometrie zwischen Grundbegriffen
und Grundvorstellungen. Jubiläumsband des Arbeitskreises Geometrie in der
Gesellschaft für Didaktik der Mathematik. S. 193-211. Springer Spektrum.
Wiesbaden, Springer Fachmedien. ISBN 978-3-658-06834-9.
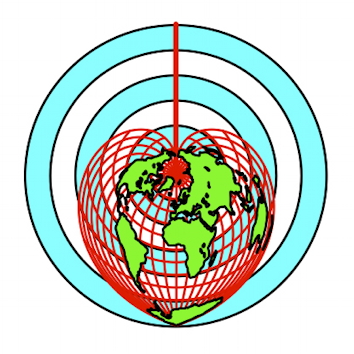
Es werden exemplarisch geometrische Beispiele aus der Ausbildung Studierender
in Geomatik, Kartografie, Vermessungswesen und
Geografie vorgestellt. Viele Beispiele mit räumlichen und sphärischen
Überlegungen sind für Schulunterricht und Begabtenförderung geeignet.
A93 2014 Hans Walser: Flächenschwerpunkte. MNU. Der
mathematische und naturwissenschaftliche Unterricht 67/8 (1.12.2014), S.
466-467. ISSN 0025-5866.
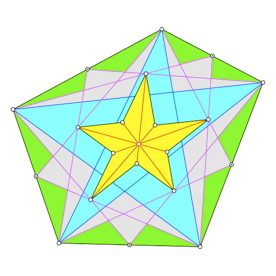
Die Konstruktion der Flächenschwerpunkte von Viereck, Fünfeck und Sechseck
führt auf überraschende Figuren.
A92 2014 Hans Walser: Höhenschnittpunkt ohne Höhen.
Die Wurzel. Zeitschrift für Mathematik. (48). 11/ 2014 . S. 247-249.

Der Höhenschnittpunkt eines Dreiecks kann ohne die Höhen konstruiert werden. Es
werden verschiedene Konstruktionen angegeben. In allen Konstruktionen spielt der
Umkreismittelpunkt eine Schlüsselrolle.
A91 2014 Hans Walser: Faltgeometrie im DIN-Format.
Jenaer Schriften zur Mathematik und Informatik. Herausgegeben von Michael
Schmitz. Friedrich Schiller Universität Jena. 06/2014.
S. 10-22.

Das DIN-Format ist mehr als ein Stück Papier und die Quadratwurzel aus Zwei.
Wir treffen auf Spiralen, Grenzpunkte, die gleichtemperierte 12-Ton-Stimmung,
das Silberne Rechteck, Faltprobleme und Legespiele nach Fröbel. Explizit werden
Faltaufgaben besprochen, die nur mit einem Papierblatt in einem DIN-Format
möglich sind. Insbesondere kommen das regelmäßige Achteck sowie Kantenmodelle
von Würfel und Tetraeder zur Sprache.
A90 2014 Johanna Heitzer und Hans Walser: Ideenkiste.
Mathematiklehren 185 / 2014. S. 50-51.
A89 2014 Hans Walser: MatheWelt.
Das Schülerarbeitsheft. Baustelle Viereck. S. 1-16. Beilage zu Mathematiklehren
185 / 2014.
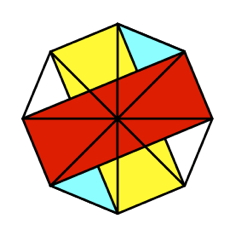
A88 2014 Johanna Heitzer und Hans Walser: Der rechte
Winkel. Mathematiklehren 185 / 2014. S. 2-9.

A87 2014 Hans Walser: Eins zu Eins – Kurzfassung
eines Vortrages im Arbeitskreis Geometrie. GDM-Mittteilungen 97 . 2014. S.
22-27.

A86 2014
Hans Walser: Rot = Blau. Aufgabe. MNU. Der mathematische und naturwissenschaftliche Unterricht
67/5 (15. 7. 2014), S. 317. ISSN 0025-5866.
A85 2014 Hans Walser: Ein Vexierbild. MNU. Der mathematische und
naturwissenschaftliche Unterricht 67/1 (15. 1. 2014), S. 29-30. ISSN 0025-5866.
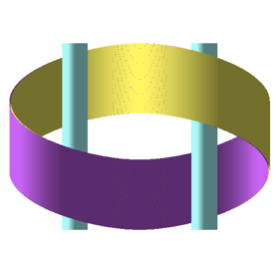
Die Geometrie einer schematischen Darstellung regt zum Nachdenken an und
fördert das räumliche Vorstellungsvermögen.
A84 2013 Manfred Pietsch und Hans Walser: Dritteln
durch Halbieren. Mathewelt. Das Schülerheft. Beilage zu: Die faszinierende Welt
der Grenzwerte. Mathematik Lehren. 180 / Oktober 2013. Pädagogische
Zeitschriften bei Friedrich in Velber in Zusammenarbeit
mit Klett.
A83 2013 Hans Walser: Vergessene Vierecke. In: Filler, Andreas / Ludwig, Mathias (Hrsg.): Wege zur
Begriffsbildung für den Geometrieunterricht. Ziele und Visionen 2020. Vorträge
auf der 29. Herbsttagung des Arbeitskreises Geometrie in der Gesellschaft für
Didaktik der Mathematik vom 14. bis 16. September 2012 in Saarbrücken.
Hildesheim : Franzbecker 2013. ISBN: 978-3-88120-589-4. S. 153-166.
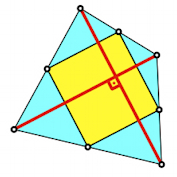
Es werden drei Vierecke vorgestellt, die im üblichen Begriffskanon wie etwa dem
Haus der Vierecke fehlen. Sie haben
nicht einmal einen Namen. Eines der drei Vierecke hat Beziehungen zu Pythagoras
(Quadratsummen), Briefumschlägen, Faltgeometrie und Wegoptimierung im Viereck.
Eingebettet in die exemplarischen Darstellungen werden allgemeine Gedanken zur
Begriffsbildung diskutiert.
A82 2013
Angel Plaza und Hans R. Walser: Proof
Without Words: Fibonacci Triangles and Trapezoids. Mathematics Magazine. 86 (2013) p. 55.
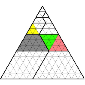
Proof of
the identity: ![]() (Fibonacci-Numbers)
(Fibonacci-Numbers)
A81 2013 Hans Walser: Die bunte Binomialverteilung.
MNU. Der mathematische und naturwissenschaftliche Unterricht 66/1 (15. 1.
2013), S. 16-18. ISSN 0025-5866.
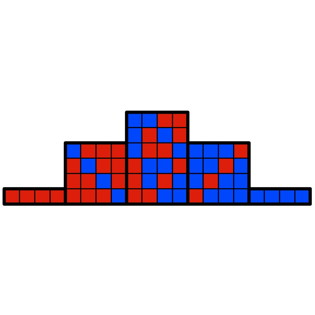
Die Histogramme der Binomialverteilung ![]() können farbig
gestaltet werden, so dass jede einzelne
Auswahlmöglichkeit von k Elementen
aus n gegebenen Elementen direkt
sichtbar wird. Die Figuren haben interessante Symmetrien und einen ästhetischen
Reiz.
können farbig
gestaltet werden, so dass jede einzelne
Auswahlmöglichkeit von k Elementen
aus n gegebenen Elementen direkt
sichtbar wird. Die Figuren haben interessante Symmetrien und einen ästhetischen
Reiz.
A80 2013 Jo Niemeyer und Hans Walser: Papierfalten,
Seilspannen, Goldener Schnitt und Hundekurve. MI, Mathematikinformation Nr. 58,
15. Januar 2013. ISSN 1612-9156. S. 3-8.
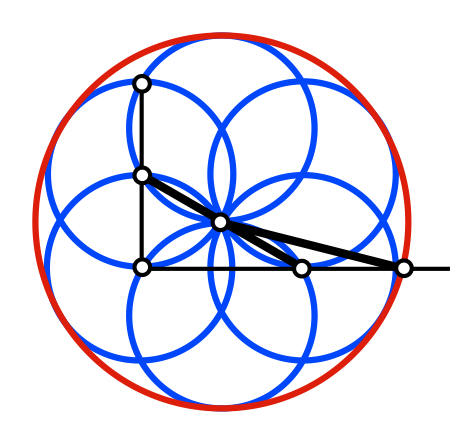
Ausgehend von einem Legespiel mit durch Falten
halbierten Blättern oder aber durch wiederholten Einsatz des von den Ägyptern
her bekannten Knotenseils kommen wir zum Goldenen Schnitt. Eine Variation des
Verfahrens führt im Grenzfall zur Traktrix.
A79 2012 Dieter Götzl und Hans Walser: Abstandssummen
am regelmäßigen n-Eck. MNU. Der mathematische und naturwissenschaftliche
Unterricht 65/8 (1. 12. 2012), S. 465-467. ISSN 0025-5866.
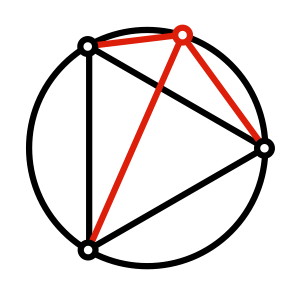
Für einen Punkt auf dem Umkreis eines regelmäßigen n-Ecks wird die Summe der
Abstände von den Eckpunkten des n-Ecks untersucht - mit durchaus erstaunlichen
Ergebnissen.
A78 2012 Hans Walser: Früh krümmt sich, was ein
Häkchen werden will. In: Filler, Andreas / Ludwig,
Mathias (Hrsg): Vernetzungen und Anwendungen im
Geometrie-Unterricht. Ziele und Visionen 2020. Vorträge auf der 28. Herbsttagung
des Arbeitskreises Geometrie in der Gesellschaft für Didaktik der Mathematik
vom 09. Bis 11. September 2011 in Marktbreit. Hildesheim : Franzbecker 2012.
ISBN: 978-3-88120-588-7. S. 95-108.
Der Krümmungsbegriff wird von verschiedener Seite her angegangen.
Vernetzung mit Schokoladekugeln, didaktischen Grundfragen,
Modellierungsproblemen in Unterricht und Praxis, Topologie, Verkehrs-Trassen
sowie einem Unesco Welterbe.
A77 2012 Hans Walser: Schwerpunkt.
Mathematikinformation Nr. 57. 15. September 2012. S. 14-22. ISSN 1612-9156.
Mathematikinformation ist eine Zeitschrift von Begabtenförderung Mathematik e.
V.
Beim Schwerpunkt treffen Geometrie und Physik aufeinander. Dies eröffnet
interessante Einsichten und Querverbindungen. Es kommen Beispiele am Dreieck
und Viereck zur Sprache. Insbesondere wird auf die Unterschiede von
Eckenschwerpunkt, Kantenschwerpunkt und Flächenschwerpunkt eingegangen.
Schließlich wird eine bemerkenswerte Gerade im Viereck vorgestellt. — Querbezüge
zwischen Bereichen der Elementargeometrie, der Mechanik und der Topologie.
A76 2012 Hans Walser: Fibonacci-Trapeze. In: Die Fibonacci-Zahlen und der goldene Schnitt. MU Der
Mathematik-Unterricht (58), Heft 1, Februar 2012, S. 19-23.

Einem regulären Sechseck werden iterativ Quadrate und gleichschenklige Trapeze
aufgesetzt. Dabei erscheinen die Fibonacci-Zahlen als Seitenlängen der Quadrate
und Trapeze. Die Trapeze führen zu einer Visualisierung der
Fibonacci-Rekursion.
A75 2012 Renato Pandi und
Hans Walser: Puzzle-Aktivitäten im Zwölfeck. MNU 65/2 (1.3.2012) S. 88-90, ISSN
0025-5866, Verlag Klaus Seeberger, Neuss.
Das regelmäßige Zwölfeck im Einheitskreis hat den Flächeninhalt 3. Dieses
unerwartet einfache Ergebnis lässt sich auf verschiedene Weisen herleiten,
insbesondere drängen sich Puzzle-Beweise auf. Zuschneiden, Verschieben und
Drehen der Puzzle-Teile fördert das zweidimensionale Vorstellungsvermögen und
bewegungsorientierte Lernprozesse. Es kommen auch Aspekte der Symmetrie und der
Ästhetik zum Tragen.
A74 2011 Hans Walser: Gleichgewichtsfiguren: Thales,
Pythagoras und Archimedes. MNU Der mathematische und naturwissenschaftliche
Unterricht 64/7 (15. 10. 2011), S. 442-443, ISSN 0025-5866.
Der Kreis des Thales und Satz des Pythagoras lassen sich auf nahe liegende
Weise verallgemeinern. Die zugehörigen Figuren haben eine
Gleichgewichtseigenschaft, sie sind in sich ruhend. Damit kommen als Querbezug
zur Physik die Hebelgesetze des Archimedes ins Spiel. Eine zentrale Rolle
spielt die Summe von Quadraten von Abständen, die wir auch in der Stochastik
(Durchschnitt, Varianz) antreffen. Bei der Organisation der Hebelmechanismen
treten Fragen der Topologie und der Kombinatorik auf.
A73 2011 Hans Walser: Proof Without Words: Fibonacci
Trapezoids. Mathematics Magazine. 84 (2011) p. 295.
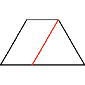
Proof of
the identity: ![]() (Fibonacci-Numbers)
(Fibonacci-Numbers)
A72 2011 Hans Walser:
Der Baustein ist das Werkzeug. In: Filler, Andreas /
Ludwig, Mathias / Oldenburg, Reinhard (Hrsg): Werkzeuge im Geometrieunterricht. Vorträge auf der
29. Herbsttagung des Arbeitskreises Geometrie in der Gesellschaft für Didaktik
der Mathematik vom 10. bis 12. September 2010 in Marktbreit. Hildesheim –
Berlin: Franzbecker 2011.

In einer arbeitsteiligen Welt sind die Grenzen zwischen Werkzeug, Rohmaterial
und Produkt fließend geworden. Das gilt insbesondere in der Geometrie bei
Verwendung von DGS (dynamische Geometrie-Software) und anderen elektronischen
Hilfsmitteln. Ein Kreis muss nicht mehr mit dem Werkzeug „Zirkel“ gezeichnet
werden, sondern steht auf Abruf bereit. Dabei wird allerdings das Werkzeug
„Zirkel“ durch das Werkzeug „Software“ ersetzt. Es werden exemplarisch gegebene
Formen wie Quadrat, gleichseitiges Dreieck, gleichschenkliges Trapez als
„Werkzeuge“ eingesetzt. Als Werk-Plattformen werden regelmäßige Raster
verwendet. Einem regulären Sechseck werden Quadrate und gleichschenklige
Trapeze aufgesetzt. Es erscheinen die Fibonacci-Zahlen und der goldene Schnitt.
Ein passendes Gelenkmodell führt zum Kehrwert einer Zahl.
A71 2011 Hans Walser: Die Modellierung des schönen
Scheins. Mathematikinformation, Nr.
55, 15. September 2011, S. 3-14. ISSN 1612-9156.
Ein Dauerbrenner in der Mathematikdidaktik ist die Frage, wie Sach- und
Anwendungsbezüge aus der so genannten realen Welt in den Schulunterricht
eingebracht werden können. Der aktuelle Lösungsansatz läuft über das Stichwort Modellierung.
In dieser Arbeit werden verschiedene Beispiele dazu kritisch untersucht.
Insbesondere wird der Unterschied zwischen Modellierung durch Funktionen
einerseits und grafischer Darstellung mit sachgemäßen Hilfsmitteln andererseits
beleuchtet. Inhaltlich kommen Spline-Funktionen,
Bézier-Kurven und Klothoiden zur Sprache.
A70 2011 Hans Walser: Winkeldefizite bei konvexen Polyedern. Mathematikinformation, Nr. 54, 15. Januar 2011, S. 44-51. ISSN 1612-9156.
Die Summe der ebenen Winkel an einer konvexen Polyederecke ist kleiner als
360°. Zu jeder Polyederecke gibt es also ein Winkeldefizit als Ergänzung auf
360°. Die Summe dieser Winkeldefizite ist konstant, nämlich 720°. Die
Gedankengänge gehen auf René Descartes (1596-1650) zurück; der Satz von
Descartes ist äquivalent zur Polyederformel von Euler. Die vorgestellten
Beispiele sind geeignet, das räumliche Vorstellungsvermögen zu schulen. Der
Beweisgang verwendet eine grundlegende Formel der sphärischen Geometrie.
Exemplarisch werden auch einige nicht konvexe Polyeder besprochen.
A69 2010 Hans Walser: Handgreifliche Modelle der Kugelgeometrie und der hyperbolischen Geometrie. MU Der Mathematikunterricht. Elemente nichteuklidischer Geometrien. Jahrgang 56. Heft 6. Dezember 2010. Friedrich Verlag, Seelze. S. 28-37.
Aus Plastik- oder Metallstreifen (Verpackungsmaterial), welche nur ein Abbiegen nach oben oder unten, aber kein seitliches Krümmen nach links oder rechts zulassen, können Modelle mit geodätische Linien gebaut werden. Im Falle der Ebene sind diese geodätischen Linien Geraden, im Falle der Kugel Großkreise und in der hyperbolischen Geometrie einfach geodätische Linien. Ausgehend von einem ebenen Geflecht mit Sechsecken und Dreiecken kommen wir durch Abbau der Eckenzahl bei den Sechsecken automatisch zu Kugeln, durch Einbau zusätzlicher Ecken aber zu Flächen mit negativer Flächenkrümmung. Die Winkeleigenschaften des sphärischen Exzesses oder des hyperbolischen Defizits werden offensichtlich, ebenso Fragen um die Existenz oder Eindeutigkeit von Parallelen.
A68 2010 Hans Walser: Vom Gleisdreieck zur Klein’schen Flasche. MNU Der mathematische und
naturwissenschaftliche Unterricht 63/8 (1. 12. 2010), S. 465-467, ISSN
0025-5866, © Verlag Klaus Seeberger, Neuss.
Es wird eine Verallgemeinerung der Klein’schen
Flasche vorgestellt, welche sich mit Grafikprogrammen einfach darstellen lässt.
Insbesondere können die Flaschen in einem Arbeitsgang hergestellt werden, ohne
Zusammensetzung aus mehreren Teilen. Die Beispiele sind geeignet, topologische
Fragen in den Unterricht einzubringen und das räumliche Vorstellungsvermögen zu
schulen. Es ergibt sich auch ein technischer Querbezug zur Astronomie.
A67 2010 Hans Walser: Legespiel mit
Schließungsfiguren. Von lokalen zu globalen Symmetrien. ml mathematiklehren
161, August 2010. S. 47-50.
Schließungsfigur: Wir wiederholen denselben Arbeitsschritt und gelangen nach
endlich vielen Schritten zur Ausgangsposition zurück. Wir haben also eine im
weitesten Sinne zyklische Symmetrie. Im Unterricht werden Schülerinnen und
Schüler mit unerwarteten Phänomenen konfrontiert, die es zu verstehen gilt.
Warum geht es auf? Ein Arbeitsschritt besteht im Beispiel dieses Artikels im
bündigen Aneinanderfügen eines beliebigen Viereckes mit Quadraten oder
gleichseitigen Dreiecken. Die Schließungsfiguren haben auch einen ästhetischen
Reiz. Lernziele: Algorithmisches Denken in konkreten Beispielen. Umgang mit
dynamischer Geometrie-Software und einfacher Grafiksoftware.
A66 2010 Hans Walser: DIN-Format und Fibonacci Zahlen.
MNU Der mathematische und naturwissenschaftliche Unterricht 63/3 (15. 4. 2010),
S. 151, ISSN 0025-5866, © Verlag Klaus Seeberger, Neuss.
Eine einfache Konstruktion mit Rechtecken im DIN Verhältnis
liefert die Fibonacci Zahlen und damit indirekt den goldenen Schnitt.
A65 2010 Hans Walser: Ein Flächensatz. In: Katja
Krüger und Philipp Ullmann (Hg.): Von Geometrie und
Geschichte in der Mathematikdidaktik. Festschrift zum 65. Geburtstag von Lutz
Führer. Eichstätt: Polygon-Verlag 2010. ISNB: 978-3-928671-60-6. S. 41-52.
Zusammenfassung. Im stumpfwinkligen und im spitzwinkligen Dreieck findet sich
ein Flächensatz, der eine gewisse Verwandtschaft zum Satz des Pythagoras
aufweist. Zwar ist der Satz des Pythagoras kein Sonderfall dieses
Flächensatzes, gleichwohl lässt sich eine Verbindung herstellen. Durch wiederholtes
Anwenden und Zeichnen des Flächensatzes entstehen logarithmische und
archimedische Spiralen.
A64 2009 Hans Walser: Die spinnen, die Mathematiker. Argumentieren,
Beweisen und Standards im Geometrieunterricht. Hrsg:
Matthias Ludwig, Reinhard Oldenburg, Jürgen Roth.AK
Geometrie 2007/08. Hildesheim, Berlin: Franzbecker 2009. ISBN
978-3-88120-487-3. S. 255-262.
Zusammenfassung: Es werden zwei Argumentationsbeispiele referiert, eines aus
dem Unterricht, das andere aus einem Pausengespräch unter Lehrer/innen und
Fachdidaktiker/innen. Dabei werden folgende Punkte angetippt. Erstens: Welches
ist das passende Medium, insbesondere die adäquate Sprache, für ein sinnvolles
Argumentieren in der Geometrie? Zweitens: Wir müssen uns von der Vorstellung
lösen, dass Argumentieren und Beweisen eine rein rationale Angelegenheit ist. Emotionale Aspekte und soziale Strukturen führen zu
Randbedingungen, unter denen ein rationaler Gedankenaustausch sehr erschwert
wird.
A63 2009 Hans Walser: Was kommt denn da von draussen rein? Argumentieren,
Beweisen und Standards im Geometrieunterricht. Hrsg:
Matthias Ludwig, Reinhard Oldenburg, Jürgen Roth. AK Geometrie 2007/08.
Hildesheim, Berlin: Franzbecker 2009. ISBN 978-3-88120-487-3. S. 143-152.
Zusammenfassung: Unter dem Kürzel HarmoS wurde
2003/04 von der kantonalen Erziehungsdirektorenkonferenz ein Projekt zur
Harmonisierung der Schulen in der Schweiz gestartet. Ich möchte das Projekt
unter folgenden externen Aspekten beleuchten: Verwendete Sprache und
Terminologie, aktuelle Schulpolitik, engagierte Personen, Akzeptanz bei
Betroffenen, Rolle und Bedeutung der Bildungsstandards.
A62 2009 Hans Walser: Fünfpunktekreise. MNU Der mathematische und naturwissenschaftliche Unterricht 62/3 (15. 4. 2009), S. 146, ISSN 0025-5866 .
A61 2009 Hans Walser: Steckmodelle. MU Der Mathematikunterricht. Polyeder im Mathematikunterricht. Jahrgang 55. Heft 1. Februar 2009. Friedrich Verlag, Seelze. S. 38-47.
A60 2008 Stephan Rosebrock und Hans Walser: Zerlegungen der Ebene und reguläre n-Ecke. Karlsruher pädagogische Beiträge. Kpg 69/2008. S. 115-125. ISSN 0724-5688
A59 2008 Hans Walser: Verquere Schülerfragen. Mathematikinformation, Nr. 49, 15. September 2008, S. 24-37. ISSN 1612-9156
A58 2007 Hans Walser: Was war vor dem Startwert? Mathematikinformation, Nr. 47, 15. September 2007, S. 63-73. ISSN 1612-9156
A57 2007 Hans Walser: Die Eulersche Gerade. Beweis ohne Worte. UNI NOVA Wissenschaftsmagazin der Universität Basel. 105 – März 2007. S. 20
A56 2006 Hans Walser: Optimierung in der Geometrie. Experimentieren im Geometrieunterricht. Hrsg: Timo Leuders und Reinhard Oldenburg. Hildesheim, Berlin: Franzbecker 2006. S. 129-146. ISBN 978-3-88120-477-4
A55 2006 Hans Walser: Innen und Außen. Mathematikinformation, Nr. 45, 15. September 2006, S. 31 – 41. ISSN 1612-9156
A54 2005 Hans Walser: Wie weit sehen wir? Praxis der Mathematik (3/47), 2005, S. 38
A53 2004 Hans Walser: Pythagoras, eine archimedische Spirale und eine Approximation von π. Praxis der Mathematik (6/46), 2004, S. 287-288
A52 2004 Heinrich Quillmann
und Hans Walser: Näherungsformeln zur Abschätzung des Umfanges gestreckter
Ellipsen. Praxis der Mathematik (6/46), 2004, S. 278
A51 2004 Hans Walser: Polyhedra from Pyramids. Math Horizons. Published by the Mathematical Association of America. November 2004. p. 15-17, 22
A50 2003 Hans Walser: Der goldene Schnitt. Mathematiklehren. Die Zeitschrift für den Unterricht in allen Schulstufen. Heft 121, Dezember 2003. S. 50 - 51
A49 2003 Alfred Hoehn und Hans Walser: Gittergeometrie und pythagoreische Dreiecke. Praxis der Mathematik (5/45), 2003, S. 215 - 217
A48 2003 Hans Walser: Eine Schar von Schnittpunkten im Dreieck. Praxis der Mathematik (2/45), 2003, S. 66 - 68
A47 2003 Hans Walser: Gleitfiguren und Gelenkfiguren. Mathematikinformation, Nr. 38, 15. Januar 2003, S. 17 - 34
A46 2000 Hans Walser: Maturitätsprüfungen in der
Schweiz. (Prüfung verfasst von Reto Schuppli.) Praxis der Mathematik (6/42), 2000, S. 263 - 266
A45 2000 Hans Walser: The Pascal Pyramid.
The College Mathematics Journal, Vol. 31, No. 5, November 2000, p. 383 -
392
A44 2000 Hans Walser: Konstruieren
mit Lineal und ”rostigem”
Zirkel. Praxis der Mathematik
(5/42), 2000, S. 227
A43 2000 Hans Walser / Dieter Wode: Diagonalenverhältnisse im regelmäßigen Vieleck. ZDM Zentralblatt für Didaktik der Mathematik. Jahrgang 32, April 2000, Heft 2, S. 36 - 37
A42 2000 Hans Walser: Lattice Geometry and Pythagorean Triangles. ZDM Zentralblatt für Didaktik der Mathematik. Jahrgang 32, April 2000, Heft 2, S. 32 - 35
A41 2000 Hans Walser: Symmetrie in Schulalltag und Theorie. Uni nova. Wissenschaftsmagazin der Universität Basel, 87, Juni 2000, S. 56 - 59
A40 2000 Hans Walser: The Pop-up Cuboctahedron. The College Mathematics Journal, Vol.
31, No. 2, March 2000, p. 89 - 92
A39 2000 Hans Walser: Gitter und ganze Zahlen. Mathematikinformation. Nr. 32, 15. Januar 2000. S. 3 – 26
A38 2000 Hans Walser: Pascal-Türme. MNU Der mathematische und naturwissenschaftliche Unterricht. 53/1 (15.1.2000), S. 12 – 17
A37 1999 Hans Walser: Folgen sehen (htm) / (pdf). Mathematik Lehren. Heft 96, Oktober 1999. S. 47-50
A36 1999 Hans Walser: Pythagoreische Dreiecke und Gittergeometrie. Beiträge zum Mathematikunterricht 1999. Vorträge auf der 33. Tagung für Didaktik der Mathematik vom 1. bis 5.3.1999 in Bern. Für die GDM herausgegeben von Michael Neubrand. Hildesheim: Franzbecker, 1999. ISBN 3-88120-304-4. S. 575-577
A35 1999 Frank Heinrich / Michael Schmitz / Hans Walser: Verallgemeinerungen der ”Möndchen des Hippokrates”. MNU Der mathematische und naturwissenschaftliche Unterricht 52/5, 1999, 264-270
A34 1999 Hans Walser: Pop Up Polyeder. MU Der Mathematik–Unterricht. Jahrgang 45. Heft 3. Mai 1999. S. 64-74
A33 1997 Hans
Walser: Stoffdruck. Beiträge
zum Mathematikunterricht: Vorträge auf der 31. Tagung für Didaktik der
Mathematik vom 3. bis 7. März 1997 in Leipzig. Für die GDM herausgegeben von
Kurt Peter Müller. Hildesheim: Franzbecker, 1997. ISBN 3-88120-284-6. S. 522-523
A32 1997 Scott Johnson and Hans Walser: The Pop-Up Octahedron. Mathematics in School. Vol. 25, No. 5, November 1997, 2-4
A31 1997 Scott Johnson and Hans Walser: Pop-Up Polyhedra. The Mathematical Gazette. Vol. 81, November 1997, 364-380
A30 1997 Peter Hilton, Jean Pedersen and Hans Walser:
The Faces of the Tri-hexaflexagon / pdf. Mathematics
Magazine. Vol. 70, October
1997, 243-251
A29 1997 Hans
Walser: Ein Zusammenhang zwischen dem DIN-A-Format und dem
goldenen Rechteck. Praxis der Mathematik (5/39), 1997, 197-198
A28 1997 Peter Hilton, Jean Pedersen and Hans Walser:
Greeting Cards and Fractals. The
Mathematical Gazette. Vol. 81, July
1997, 252-262
A27 1997 Scott Johnson and Hans Walser: Collapsible
cubes and other curiosities. The
Australian Mathematics Teacher (vol. 53, no 1, 1997), 34-37
A26 1997 Hans Walser: Permutationen und Raumgeometrie. MNU Der mathematische und naturwissenschaftliche Unterricht 50/2, 1997, 74-76
A25 1996 Hans Walser: Geschlossene Korbbögen. Praxis der Mathematik (38), 1996, 169-172
A24 1996 Hans Walser: Individuelle Semesterarbeiten im Fach Mathematik. VSMP-Bulletin 71, 31-33
A15a 1995 Hans Walser: Geometrie zum Anfassen. In Trends im Geometrieunterricht. Tagungsband der Zwölften Tagung des GDM-Arbeitskreises Geometrie im Unterricht in VISEGRAD 29. 09. – 03. 10. 1995.
A23 1995 Hans Walser: Pythagoreische Dreiecke in der Gittergeometrie. Didaktik der Mathematik (23), 1995, 193-205
A22 1994 Hans Walser: Periodizität bei der Newton-Rekursion. Die Wurzel (28, Heft 12/94), 270-271
A21 1994 Hans Walser: Geometrie zum Anfassen - Flechtmodelle für Polyeder. Tagungsband der Herbsttagung 1994 von VDBiol und MNU in Konstanz, 39-46
A20 1994 Hans Walser: Geometrie zum Anfassen. Mathematik Lehren, Heft 65, Aug. 1994, 56-59
A19 1994 Hans Walser: Eine Verallgemeinerung der Winkelhalbierenden. Didaktik der Mathematik (22), 1994, 50-56
A18 1993 Hans Walser: Reguläre Vielecke in der Rastergeometrie. Didaktik der Mathematik (21), 1993, 230-237
A17 1993 Hans Walser: Die Eulersche Gerade als Ort "merkwürdiger Punkte". Didaktik der Mathematik (21), 1993, 95-98
A16 1993 Martin Huber, Ueli Manz, Hans Walser: Annäherung an den Goldenen Schnitt. Berichte über Mathematik und Unterricht, Bericht 93-01, ETH-Zürich
A15 1993 Hans Walser: Geometrie zum Anfassen. Beiträge zum Mathematikunterricht. Vorträge auf der 27. Bundestagung für Didaktik der Mathematik vom 22. bis 26. 3. 1993 in Freiberg/Schweiz. Verlag Franzbecker, Hildesheim. 366-369
A14 1993 Hans Walser: Eine spezielle Klasse von Parallelogrammen. MNU Der mathematische und naturwissenschaftliche Unterricht 46/3, 1993, 163-164
A13 1993 Hans Walser: Geometrische Schließungsfiguren im Unterricht. Praxis der Mathematik (35), 1993, 77-84
A12 1991 Hans Walser: Schließungsfiguren. Didaktik der Mathematik (19), 1991, 187-206
A11 1991 Hans Walser: Ein Schnittpunktsatz. Praxis der Mathematik (33), 1991, 70-71
A10 1990 bis 1994 Hans Walser: Schlußpunkt (Geometrische "Comic-strips"). Didaktik der Mathematik (18 bis 22)
A09 1989 Hans Walser: Fraktale. Berichte über Mathematik und Unterricht, Bericht 89-01, ETH-Zürich
A08 1988 Hans Walser: Ein Schließungssatz der Elementargeometrie. Elemente der Mathematik (43), 1988, 161-169
A07 1987 Hans Walser: Der Goldene Schnitt. Didaktik der Mathematik (15), 1987, 176-195
A06 1987 Hans Walser: Flechtmodelle. Didaktik der Mathematik (15), 1987, 1-17
A05 1985 Hans Walser: Stirlingsche Zahlen im Unterricht. Didaktik der Mathematik (13), 1985, 150-168
A04 1983 Hans Walser: Ein Zerlegungssatz für punktsymmetrische konvexe Vielecke. Elemente der Mathematik (38), 1983, 159-160
A03 1980 Hans Walser: Der Einsatz von programmierbaren Taschenrechnern im Unterricht. Didaktik der Mathematik (8), 1980, 27-38
A02 1976 Hans Walser: Eine Übertragung der Formel von Gauß-Bonnet auf ebene Netze. Elemente der Mathematik (31), 1976, 59-64
A01 1975 Hans Walser: Reguläre Kreisnetze. Didaktik der Mathematik (3), 1975, 121-133