Hans Walser
Schnittpunkte 301-400
Die Bildsequenzen sind im Sinne einer ãminimal artÒ als Bilder ohne Worte konzipiert. Dabei wurde folgende grafische Systematik verwendet:

Die drei kleinen Bilder im Querstreifen deuten die Entstehung der Gesamtfigur an.
Gegebenenfalls finden sich unterhalb der Figur Literaturangaben oder Hinweise auf Anregungen, die zu diesen Figuren gefhrt haben.
Schnittpunkt
301
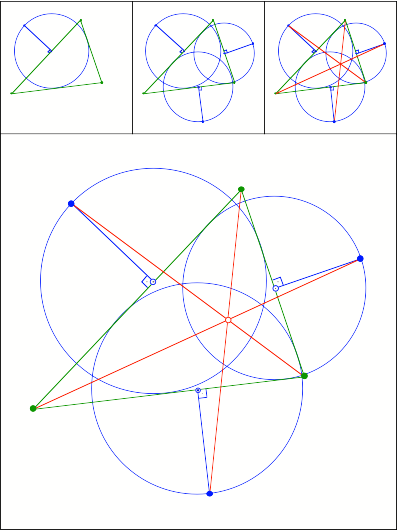
Schnittpunkt
302
Einbeschriebene Halbkreise
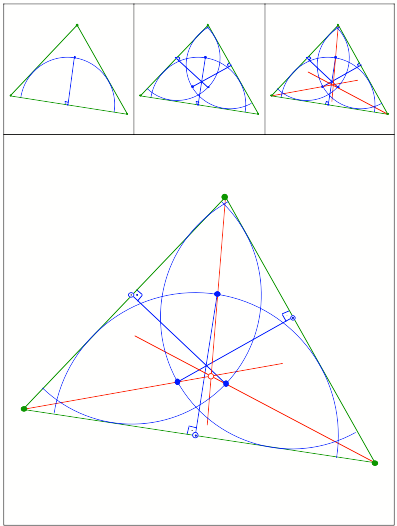
Schnittpunkt
303
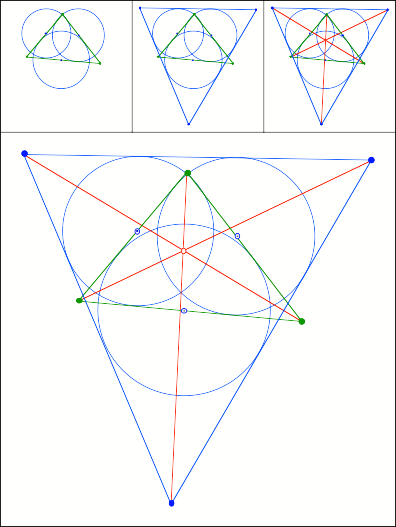
Schnittpunkt
304
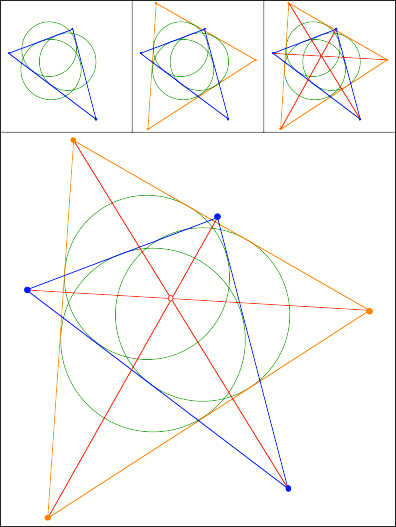
Schnittpunkt
305
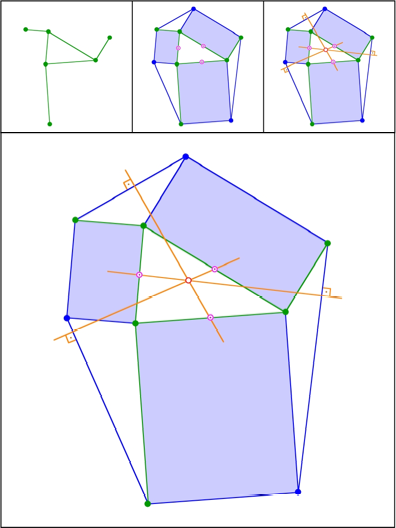
Aufgesetzte Rechtecke
Schnittpunkt
306
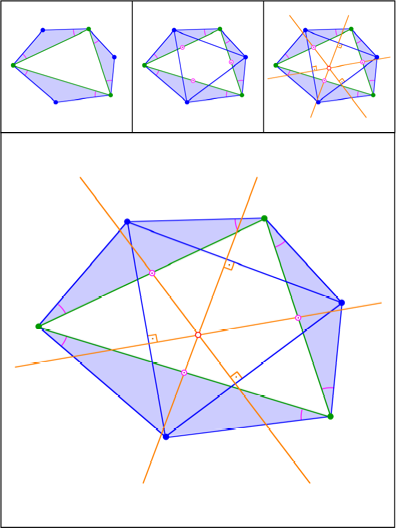
Aufgesetzte gleichschenklige Dreiecke
Schnittpunkt
307
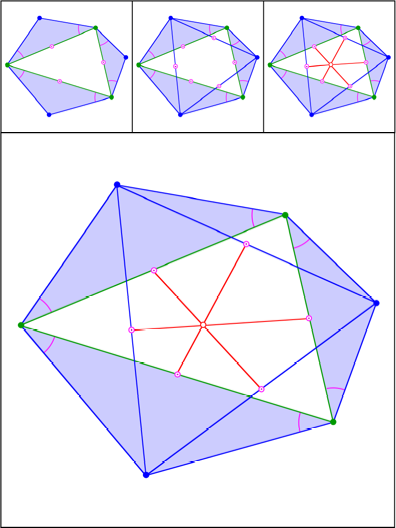
Aufgesetzte gleichschenklige Dreiecke
Schnittpunkt
308
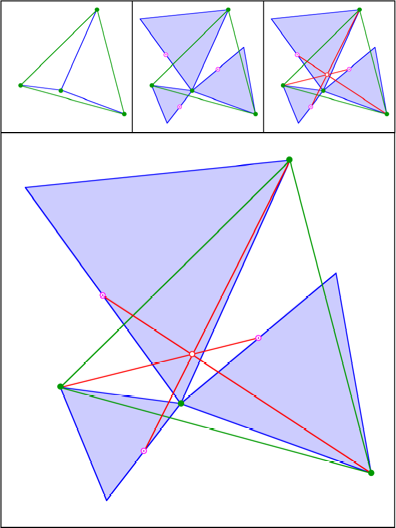
Gleichseitige Dreiecke
Schnittpunkt
309
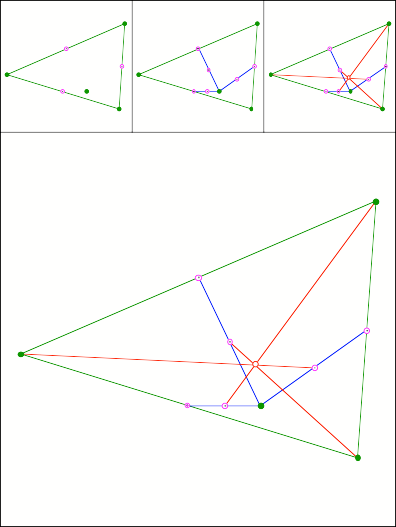
Schnittpunkt
310
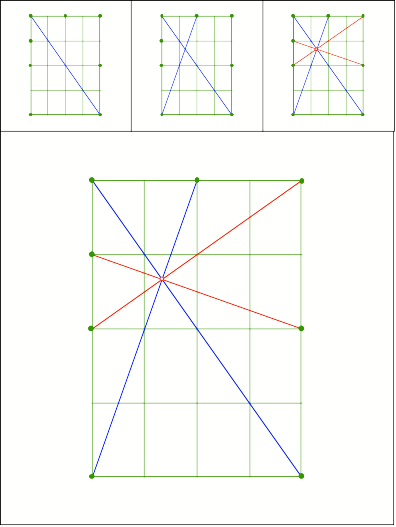
DIN Format
Schnittpunkt
311
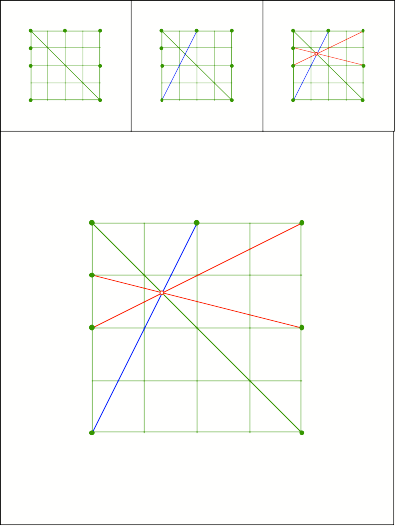
Schnittpunkt
312
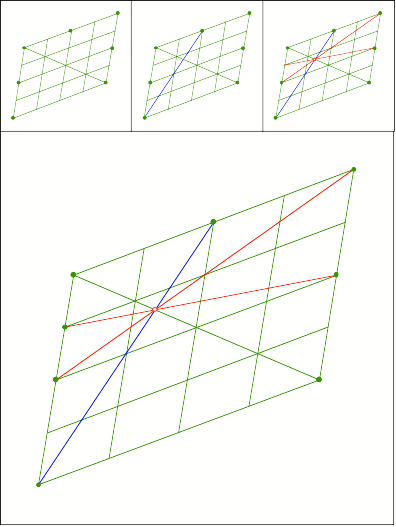
Schnittpunkt
313
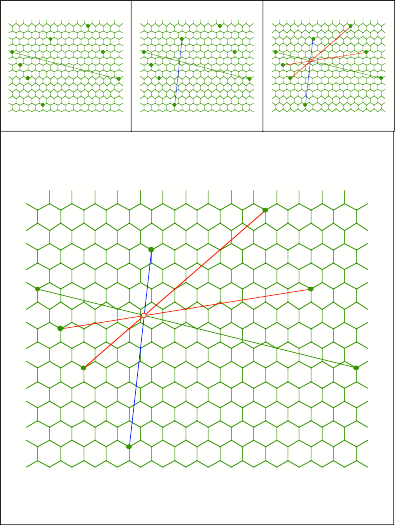
Schnittpunkt
314
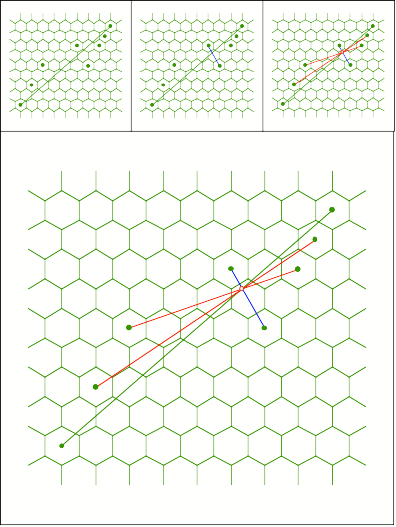
Schnittpunkt
315
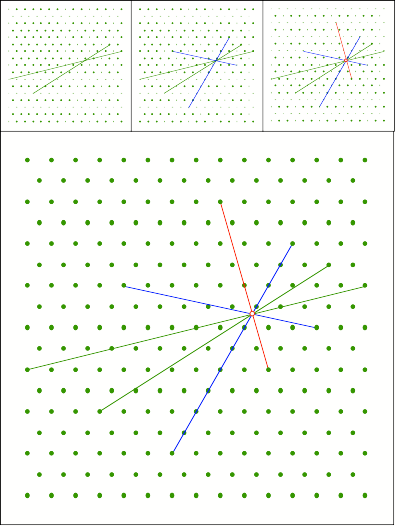
Schnittpunkt
316
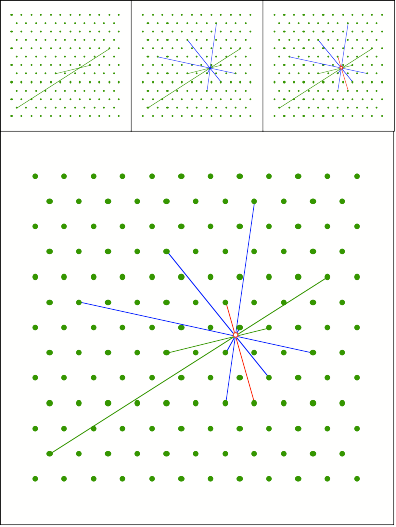
Schnittpunkt
317
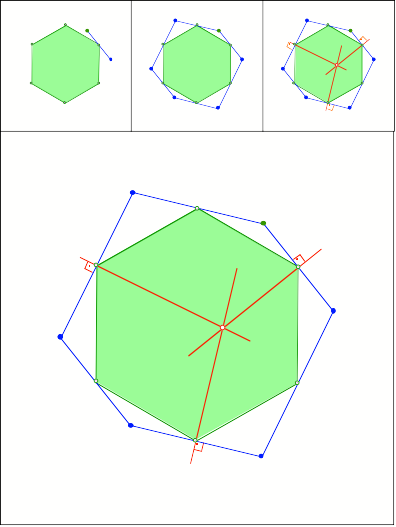
Schnittpunkt
318
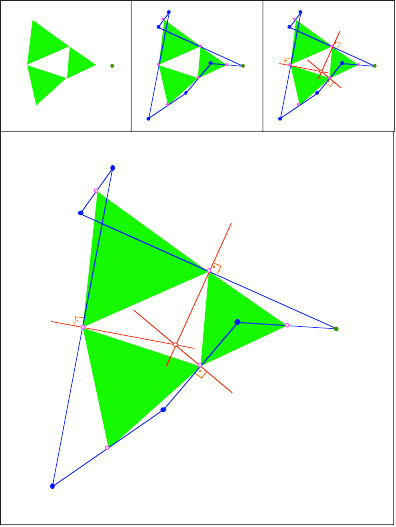
Schnittpunkt
319
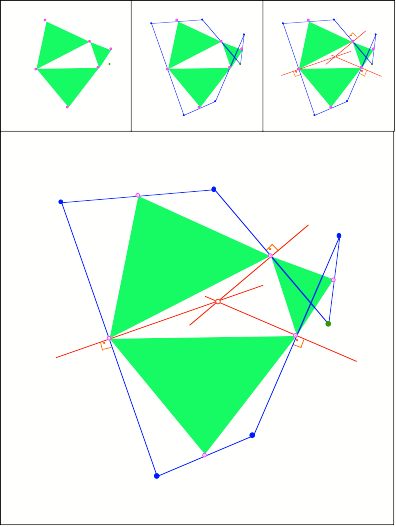
Schnittpunkt
320
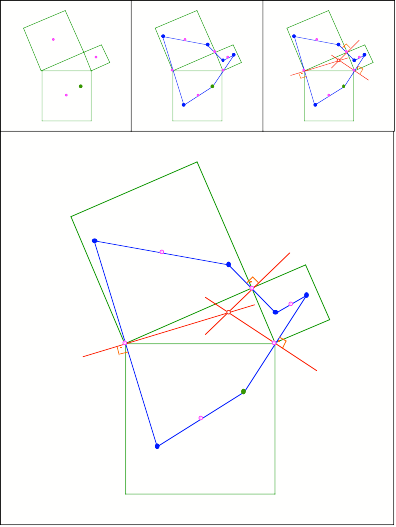
Schnittpunkt
321
![]()
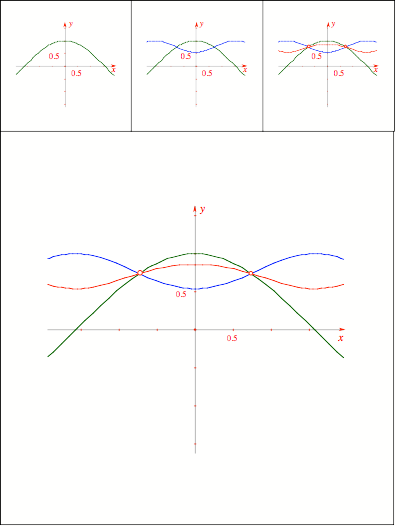
Schnittpunkt
322
![]()
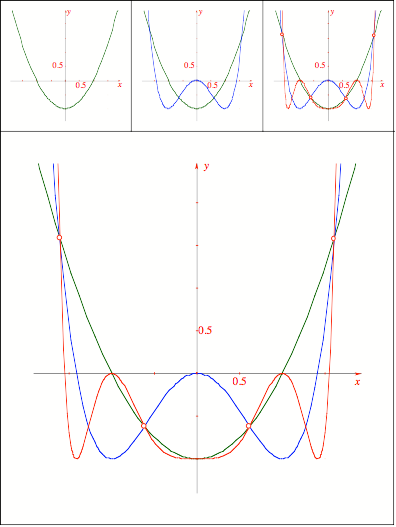
Schnittpunkt
323
![]()
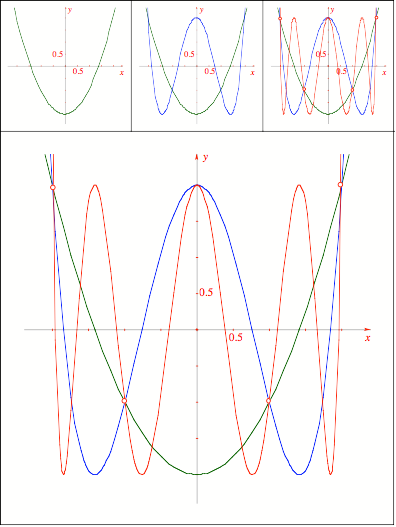
Schnittpunkt
324
![]()
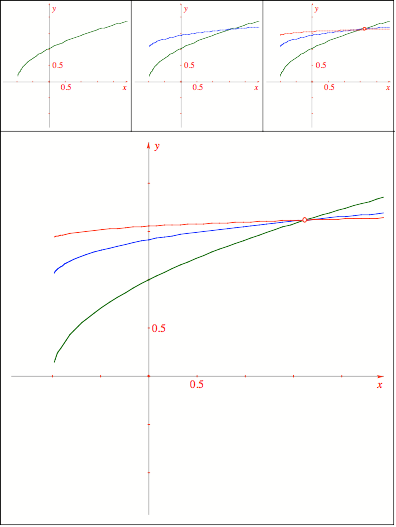
Schnittpunkt
325
![]()
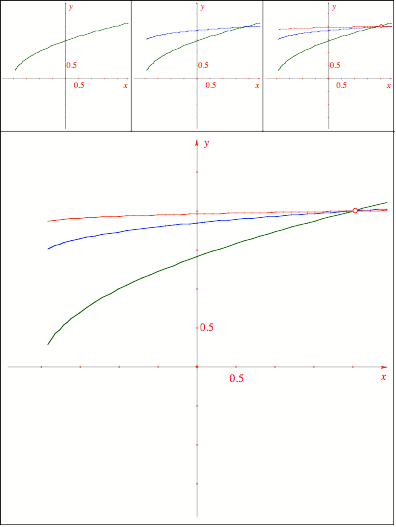
Schnittpunkt
326
![]()
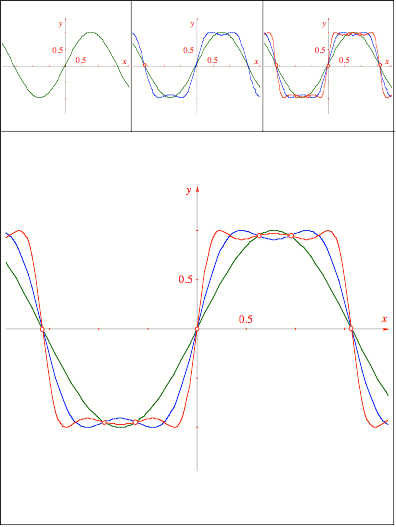
Schnittpunkt
327
![]()
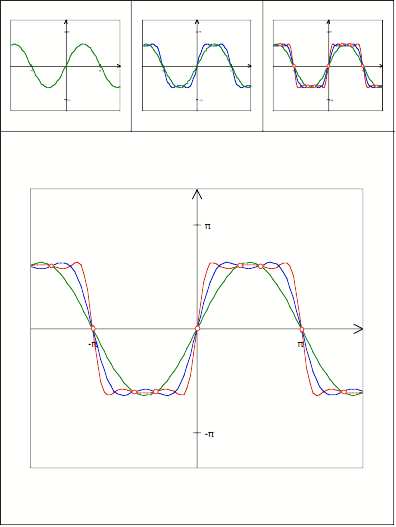
Schnittpunkt
328
![]()
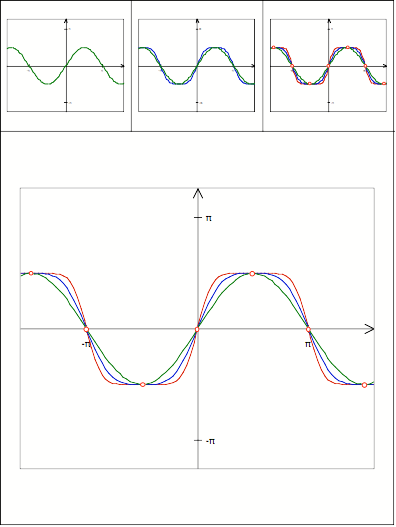
Schnittpunkt
329
![]()
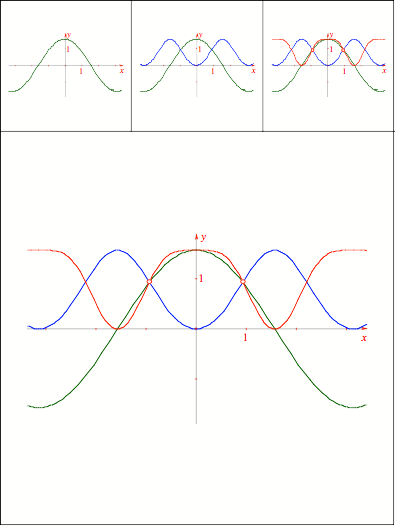
Schnittpunkt
330
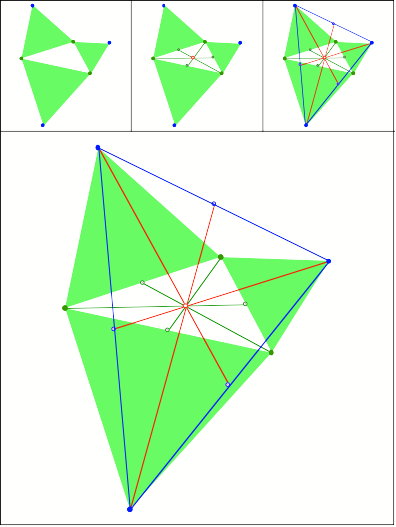
Schnittpunkt
331
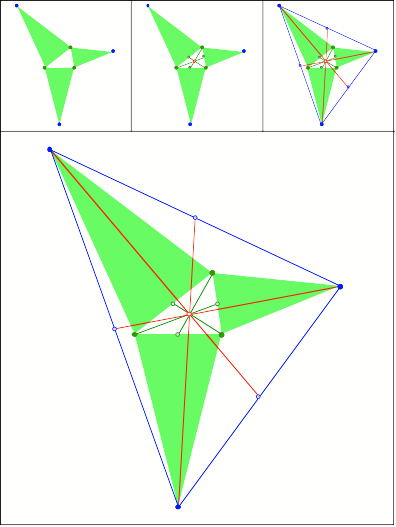
Schnittpunkt
332
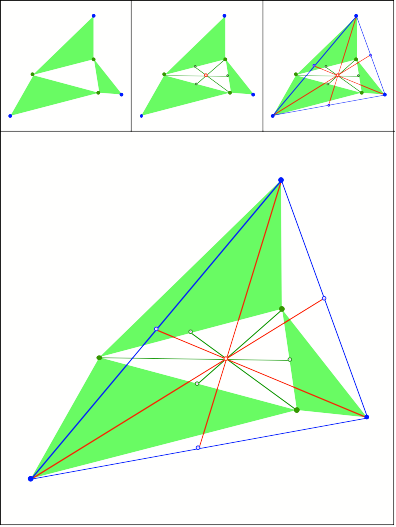
Schnittpunkt
333
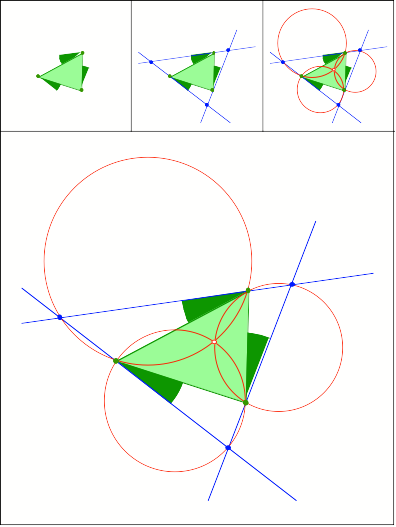
Anregung: Dieter Gtzl
Schnittpunkt
334
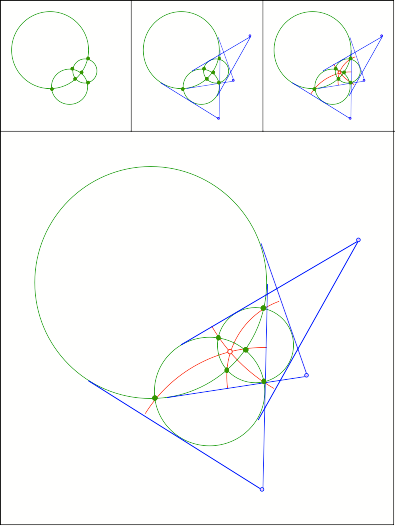
Anregung: Pierre Bolli
Schnittpunkt
335
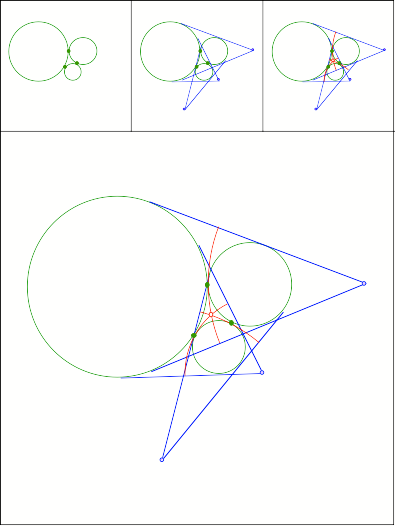
Schnittpunkt
336
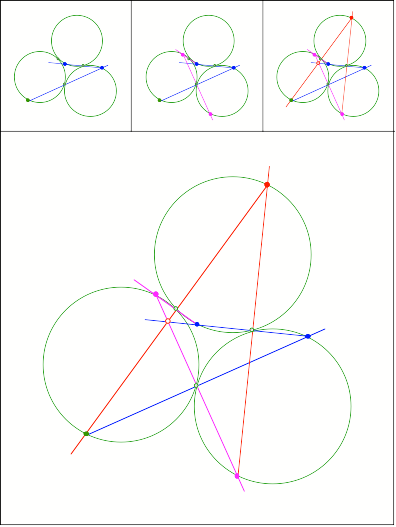
Drei gleich gro§e Kreise. Wie gro§ sind die auftretenden Winkel?
Schnittpunkt
337
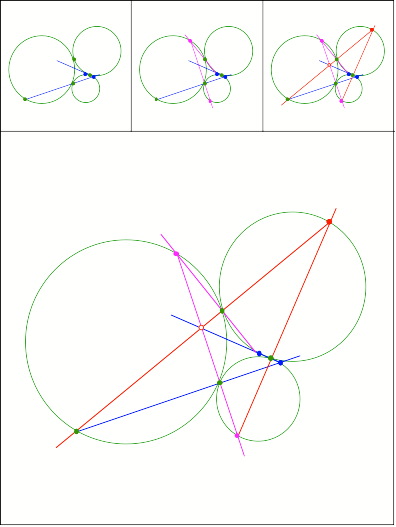
Schnittpunkt
338
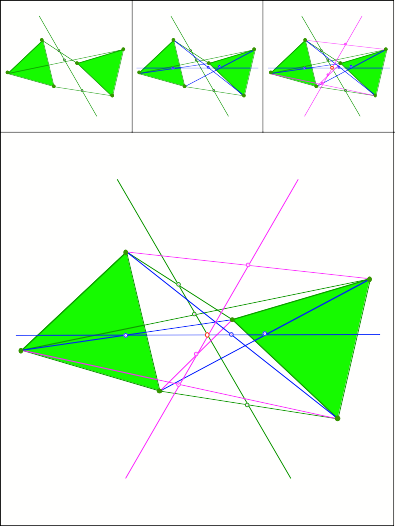
Schnittpunkt
339
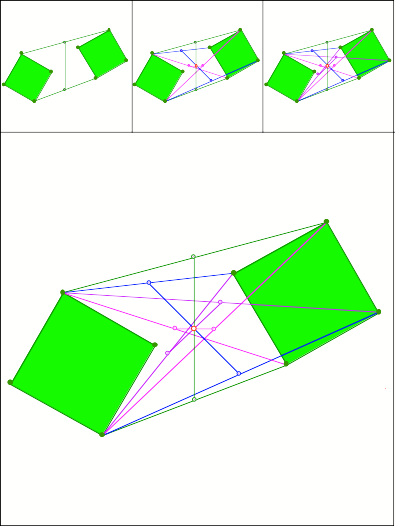
Anregung: Heiner Bubeck
Schnittpunkt
340
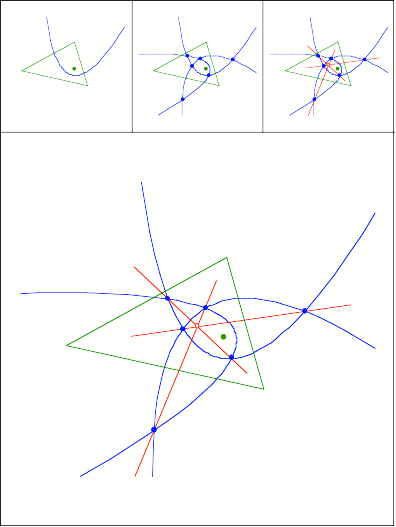
Schnittpunkt
341
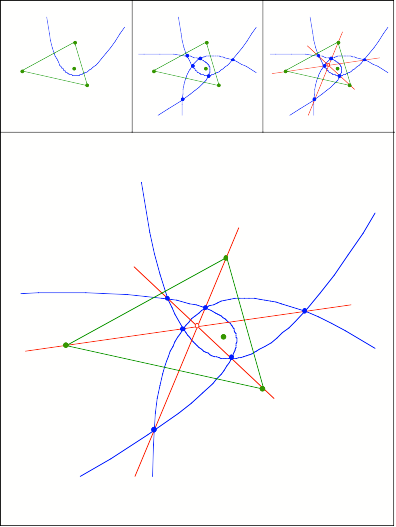
Konfokale Parabeln
Schnittpunkt
342
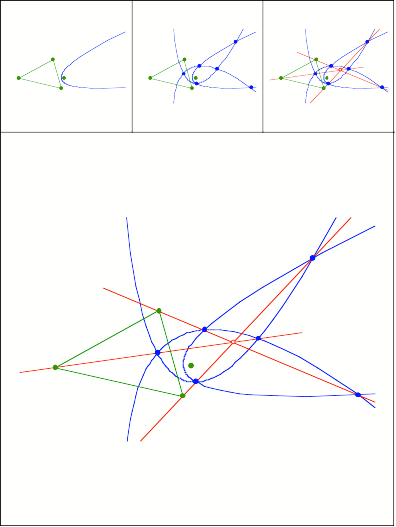
Konfokale Parabeln
Schnittpunkt
343
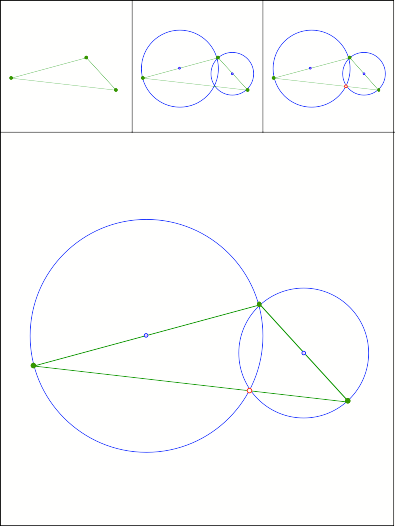
Schnittpunkt
344
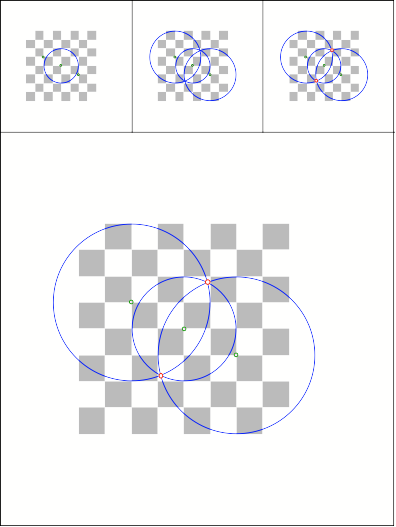
Anregung: Joe Niemeyer
Schnittpunkt
345
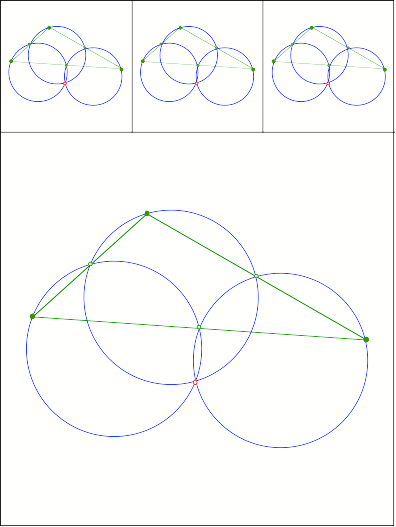
Miguel, Sonderfall
Schnittpunkt
346
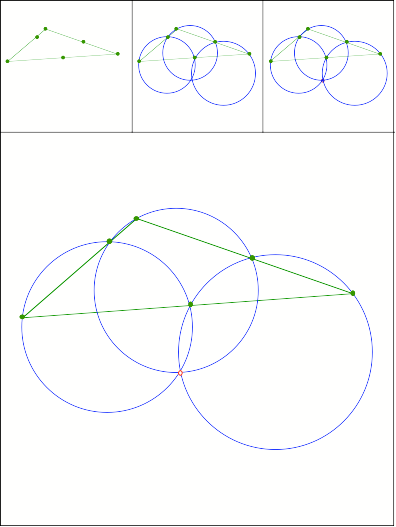
Miguel
Schnittpunkt
347
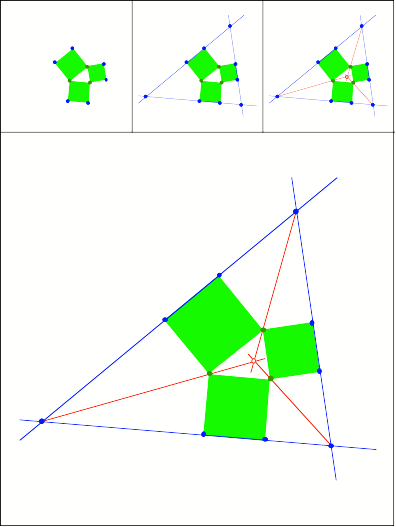
Schnittpunkt
348
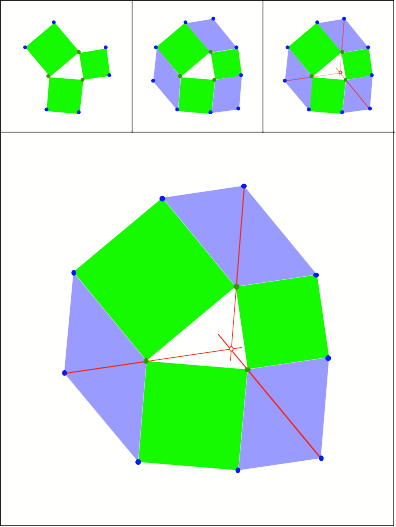
Schnittpunkt
349
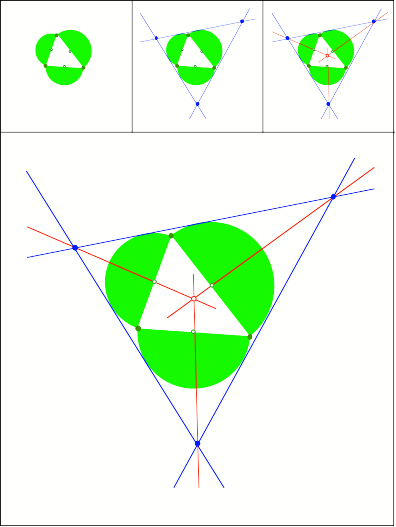
Schnittpunkt
350
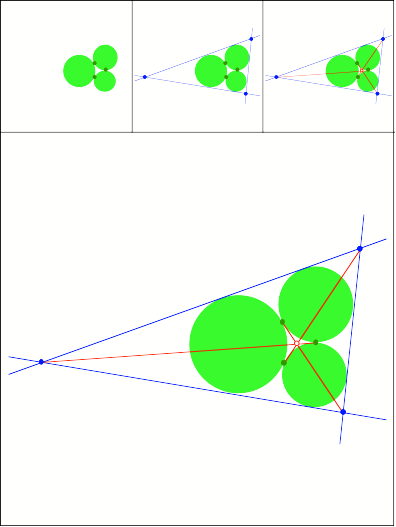
Schnittpunkt
351
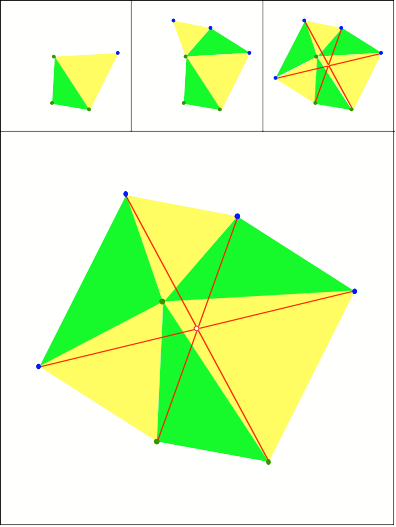
Ein Dreieck und drei
gleichseitige Dreiecke
Schnittpunkt
352
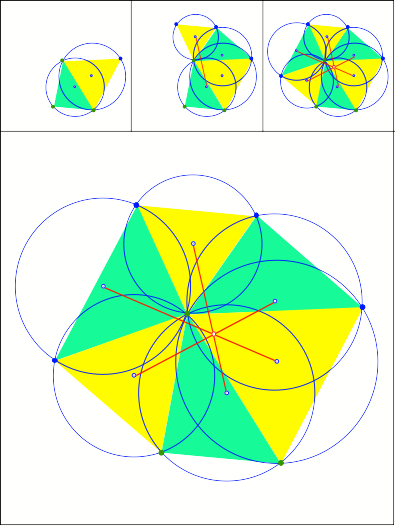
Ein Dreieck und drei
gleichseitige Dreiecke mit Umkreisen
Schnittpunkt
353
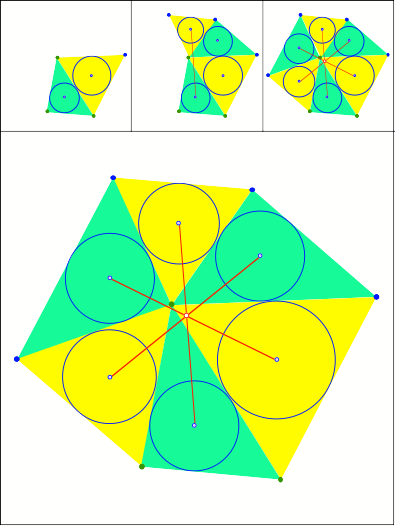
Ein Dreieck und drei
gleichseitige Dreiecke mit Inkreisen
Schnittpunkt
354
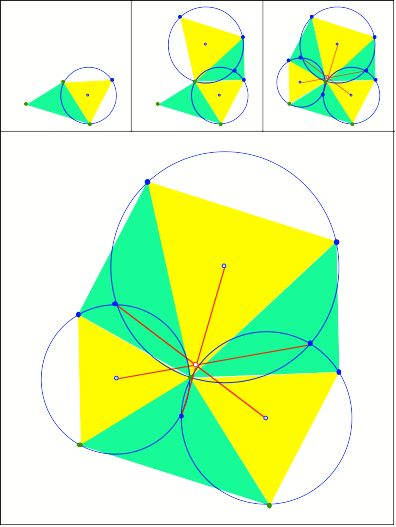
Ein Dreieck und drei
gleichseitige Dreiecke mit Umkreisen
Schnittpunkt
355
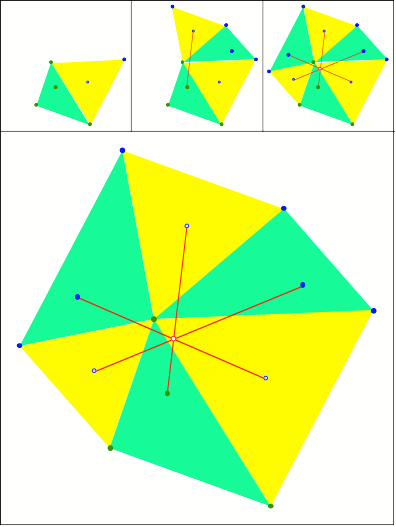
Beliebiger Punkt im
grnen Dreieck
Schnittpunkt
356
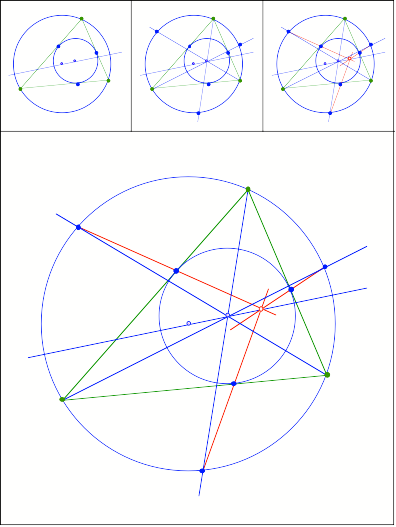
Mitteilung: Hans-Joachim Rein
Schnittpunkt
357
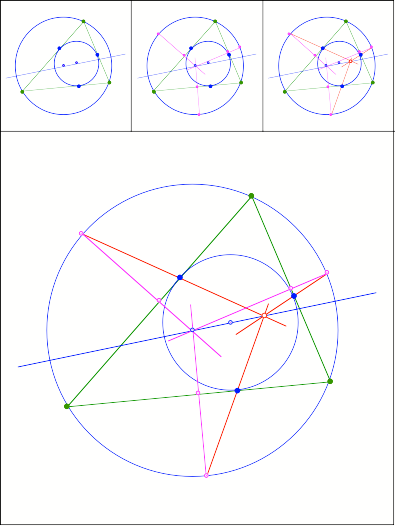
Anregung: Hans-Joachim Rein
Schnittpunkt
358
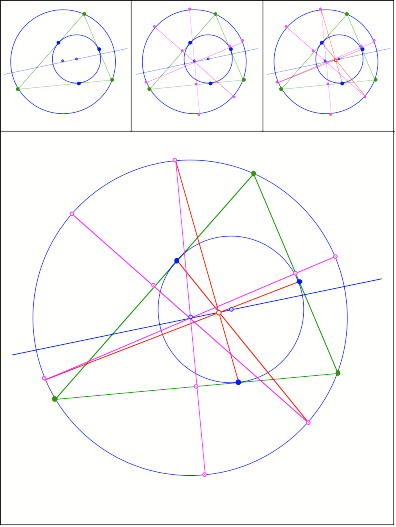
Anregung: Hans-Joachim Rein
Schnittpunkt
359
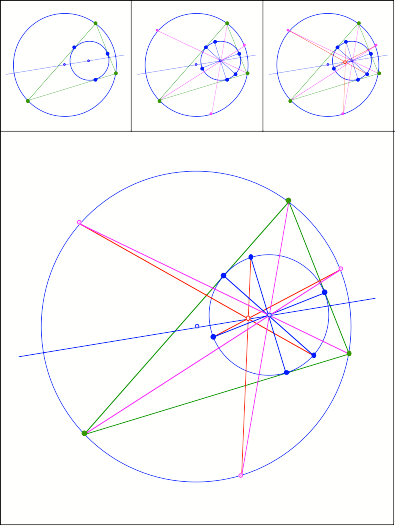
Anregung: Hans-Joachim Rein
Schnittpunkt
360
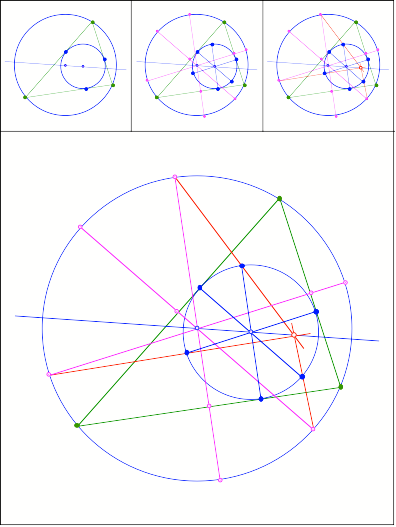
Anregung: Hans-Joachim Rein
Schnittpunkt
361
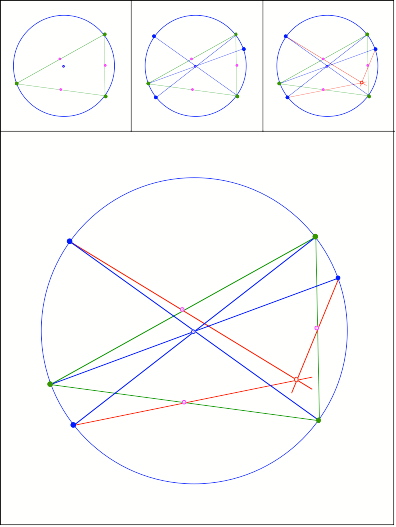
Tipp: Hhenschnittpunkt
Schnittpunkt
362
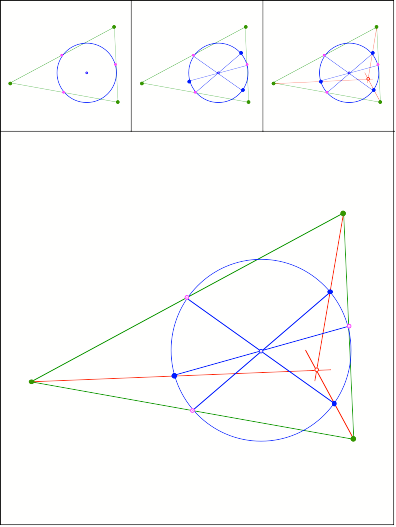
Tipp:
Hhenschnittpunkt. Feuerbachkreis
Schnittpunkt
363
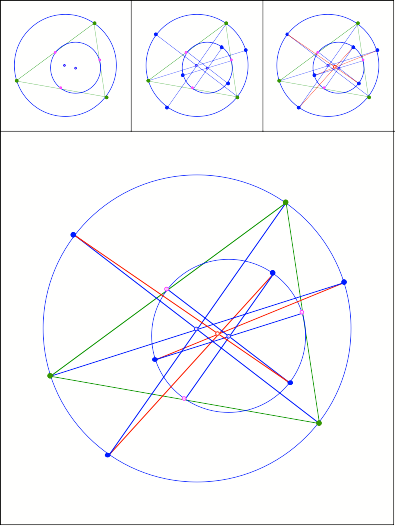
Schnittpunkt
364
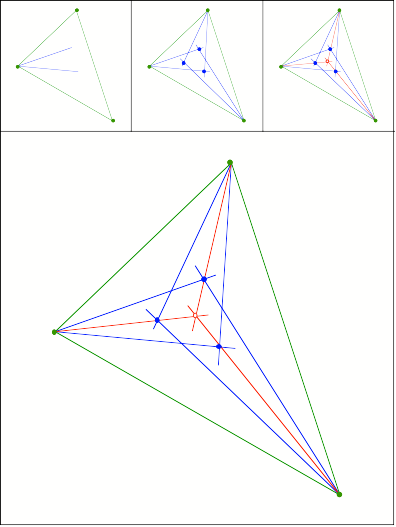
Winkeldrittelung; geht
nicht mit Zirkel und Lineal
Schnittpunkt
365
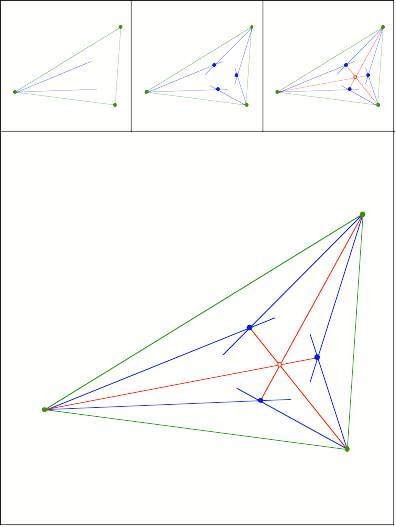
Winkelviertelung
Schnittpunkt
366
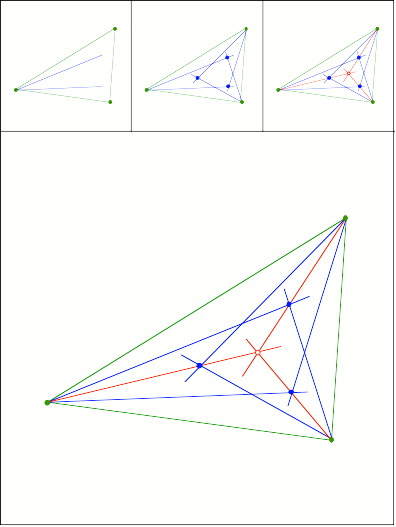
Winkelviertelung
Schnittpunkt
367
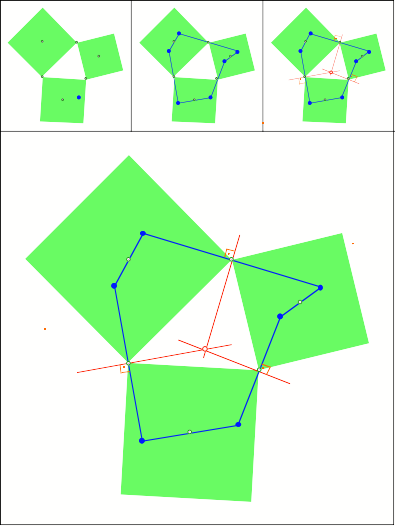
Anregung: Michael Bauer,
Wei§enburg
Schnittpunkt
368
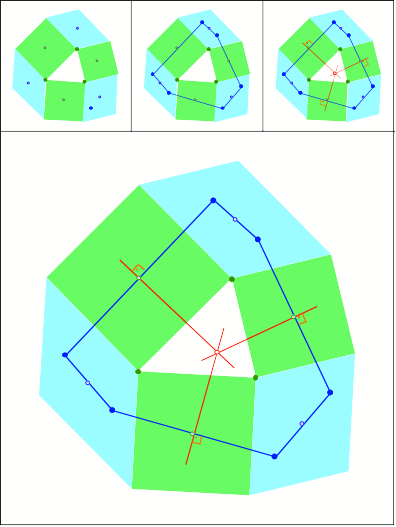
Schnittpunkt
369
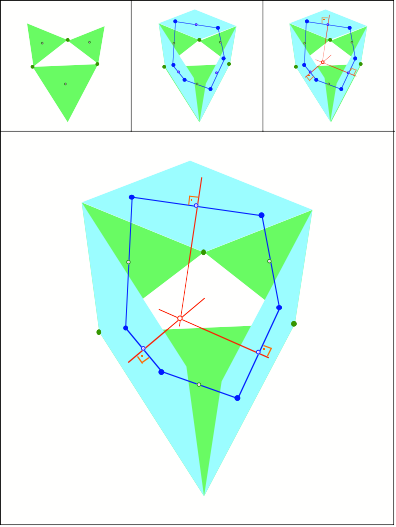
Schnittpunkt
370
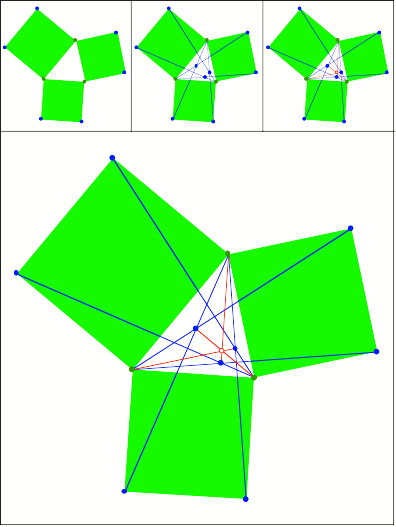
Schnittpunkt
371
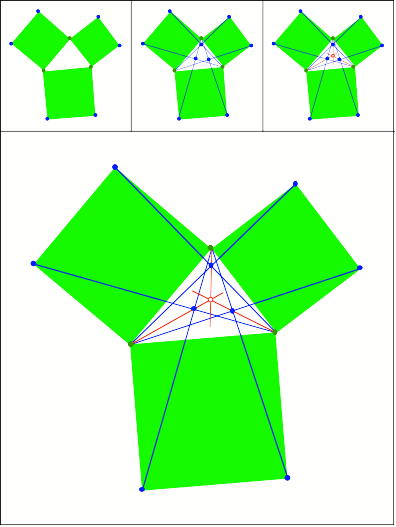
Schnittpunkt
372
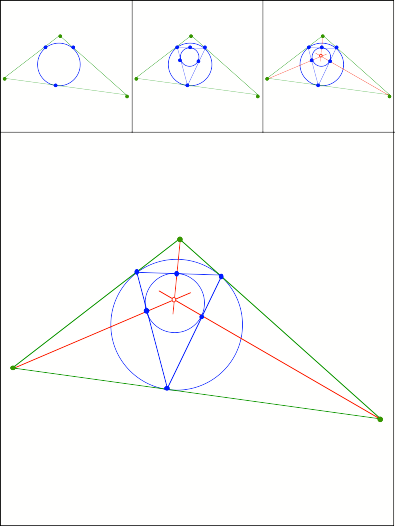
Schnittpunkt
373
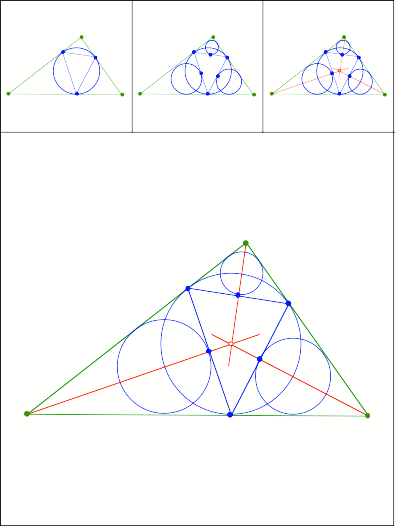
Schnittpunkt
374
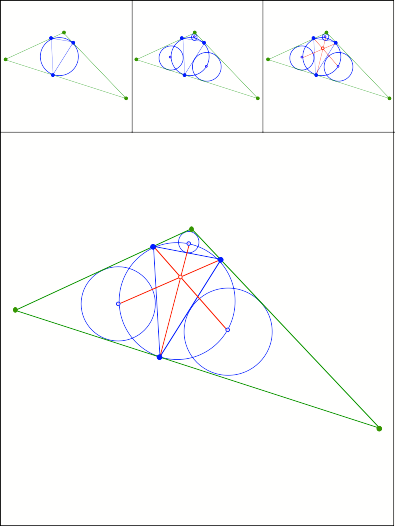
Schnittpunkt
375
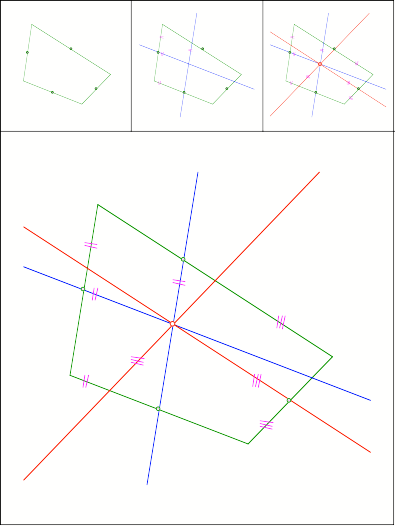
Schnittpunkt
376
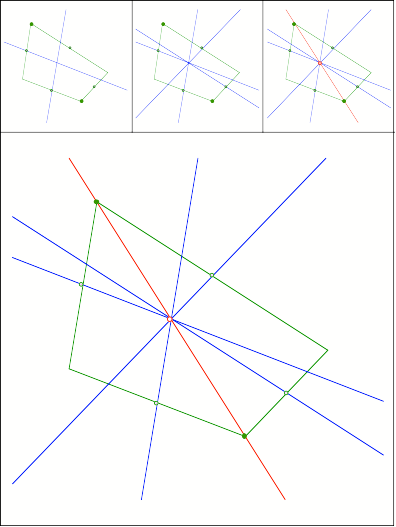
Schnittpunkt
377
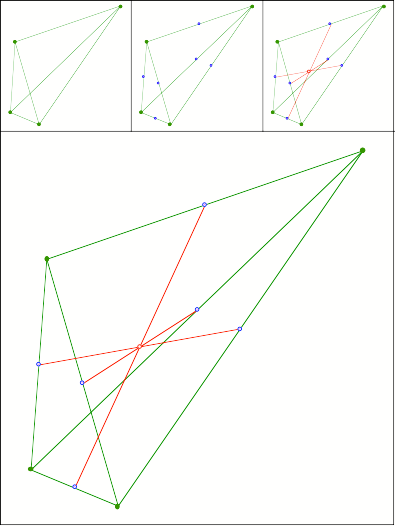
Schnittpunkt
378
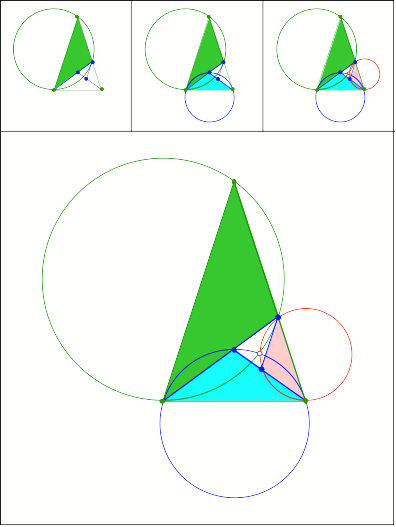
Goldener Schnitt
Schnittpunkt
379
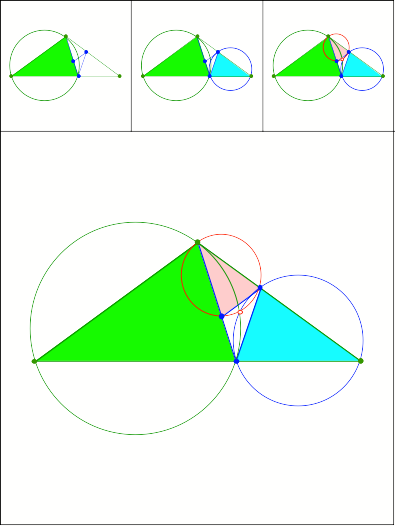
Goldener Schnitt
Schnittpunkt
380
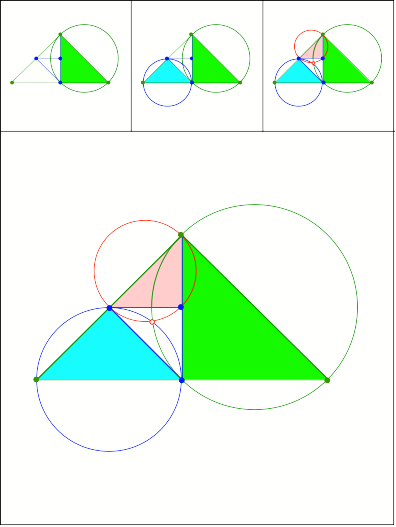
Thaleskreise
Schnittpunkt
381
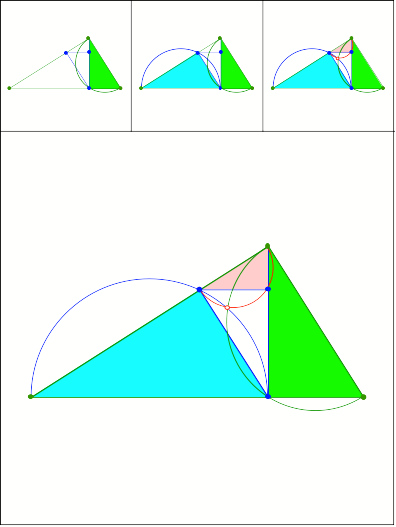
Schnittpunkt
382
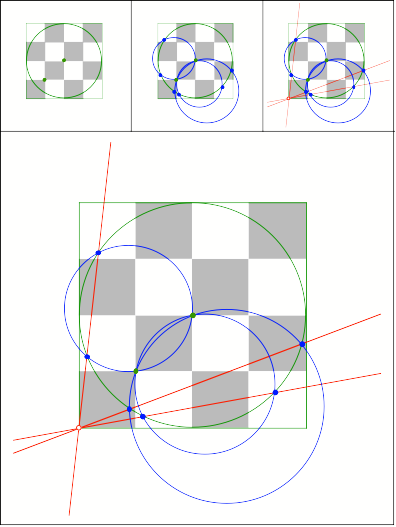
Schnittpunkt
383
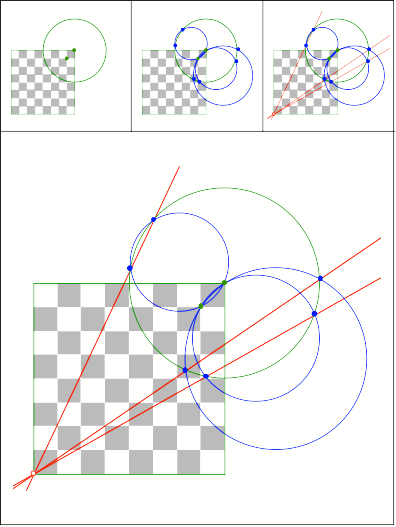
Schachbrett
Schnittpunkt
384
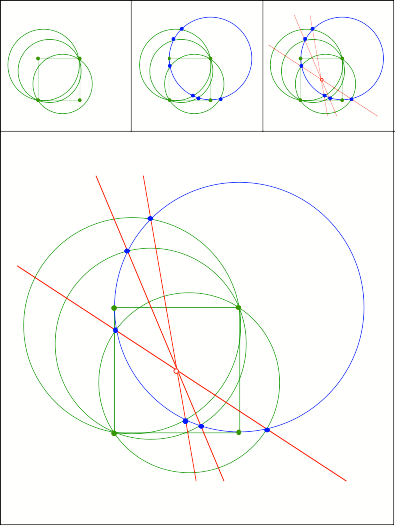
Schnittpunkt
385
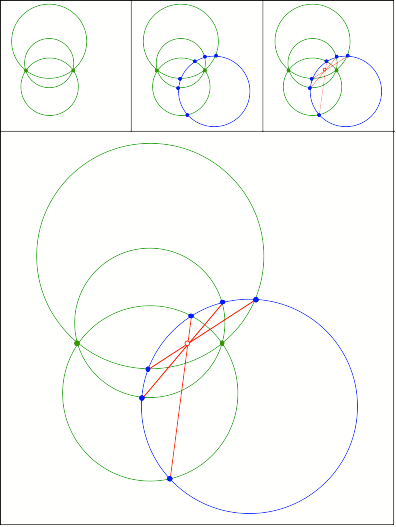
Kreisbschel
Schnittpunkt
386
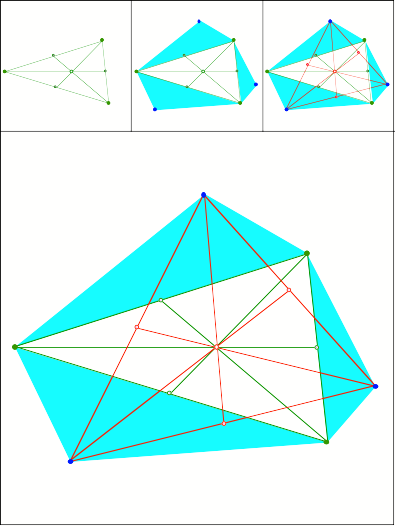
Aufsetzen hnlicher
Dreiecke
Schnittpunkt
387
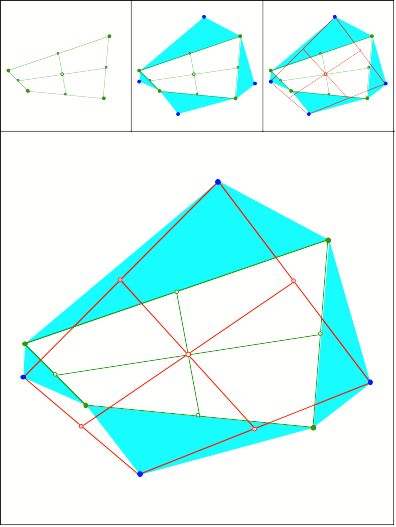
Aufsetzen hnlicher
Dreiecke
Schnittpunkt
388
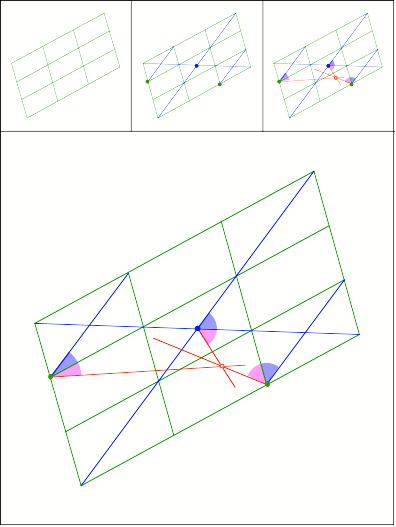
Schnittpunkt
389
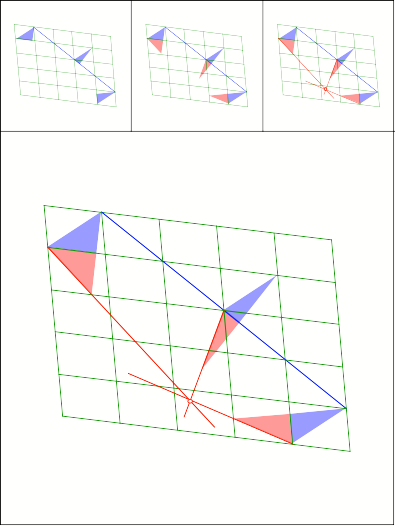
Schnittpunkt
390
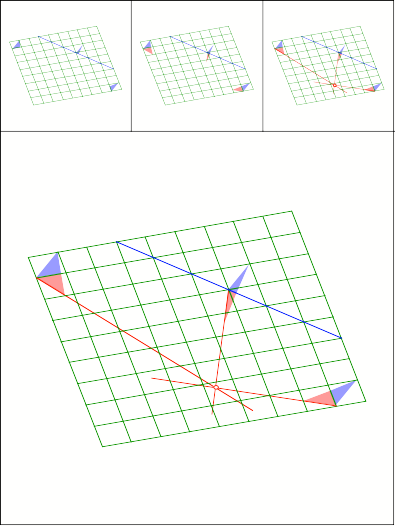
Schnittpunkt
391
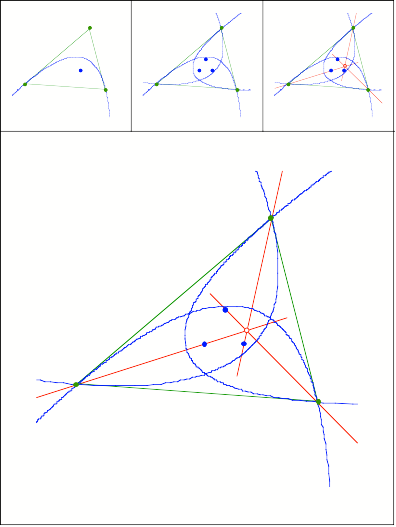
Brennpunkte der Inparabeln
Schnittpunkt
392
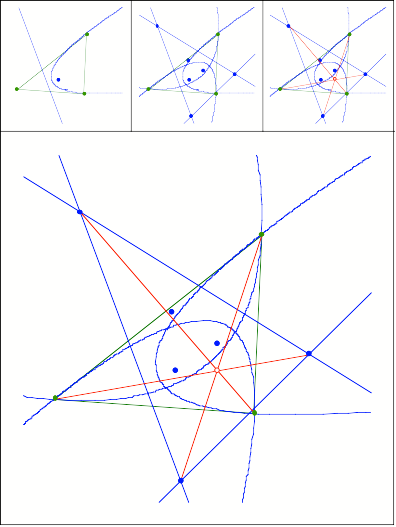
Leitliniendreieck der
Inparabeln
Schnittpunkt
393
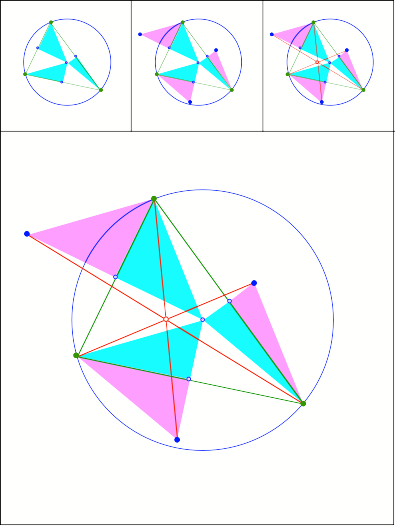
Der Schnittpunkt ist
das Zentrum des Feuerbachkreises
Schnittpunkt
394
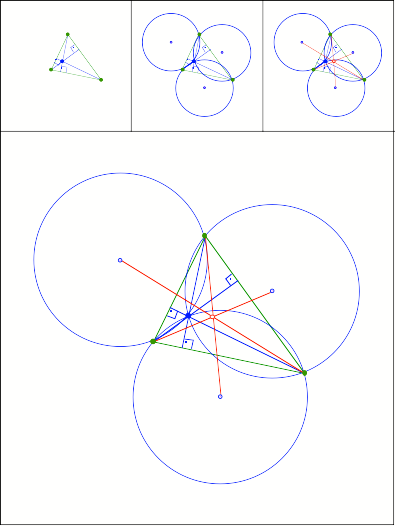
Der Schnittpunkt ist
das Zentrum des Feuerbach-Kreises
Schnittpunkt
395
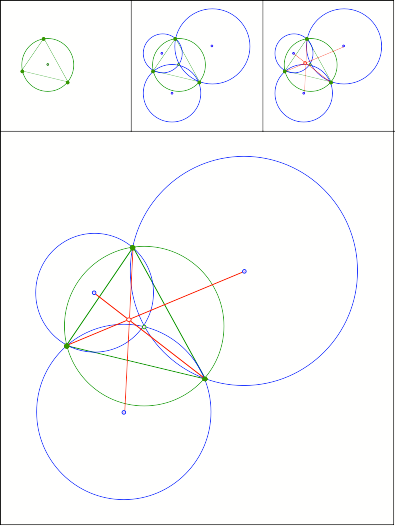
Schnittpunkt
396
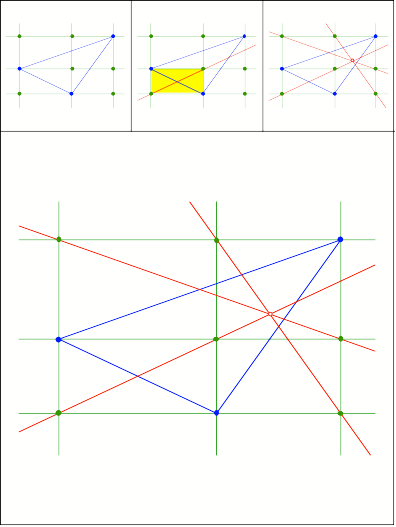
Anregung: [Wildberger 2010]
Schnittpunkt 397
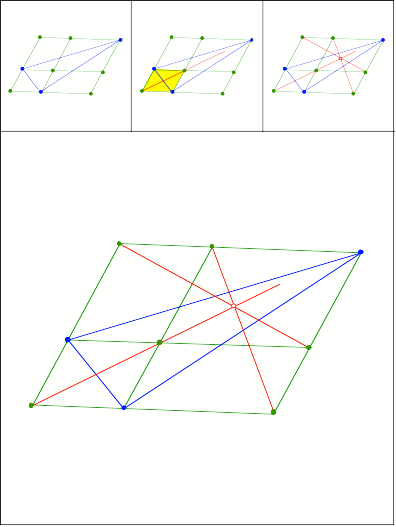
Schnittpunkt 398
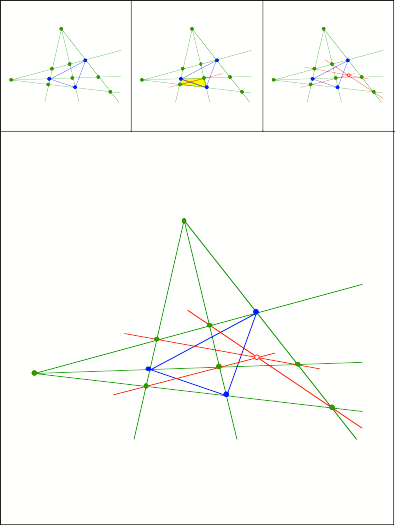
Schnittpunkt
399
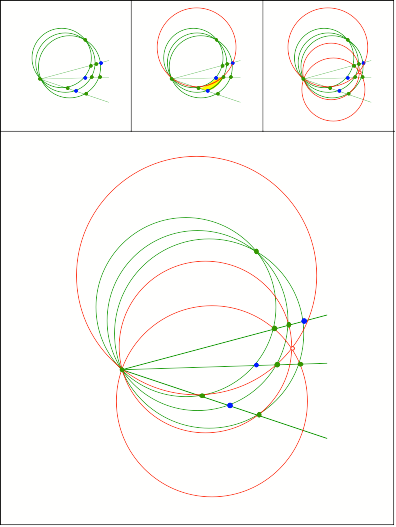
Schnittpunkt
400
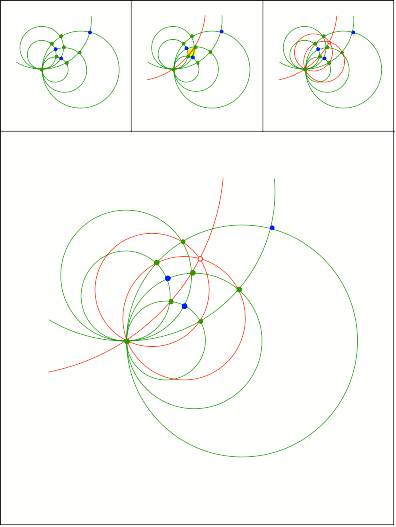
Literatur
[Baptist 1992] Baptist, Peter: Die Entwicklung der neueren Dreiecksgeometrie. Mannheim: B.I.Wissenschaftsverlag 1992. ISBN 3-411-15661-9
[Donath 1976] Donath, Emil: Die merkwrdigen Punkte und Linien des ebenen Dreiecks. Berlin: Deutscher Verlag der Wissenschaften, 3. Auflage 1976.
[Eddy/Fritsch 1994] Eddy, R.H. / Fritsch, R.: The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June 1994, p. 188-205
[Euklid 1980] Euklid: Die Elemente. Nach Heibergs Text aus dem Griechischen bersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft 1980. ISBN 3-534-01488-X
[G.-M. 1920/1991] G.-M., F.: Exercices de Gomtrie. Sixime dition. Tours - Paris: Mame - de Gigord 1920. Rimpression de la 6e dition publie par Mame et De Gigord en 1920. Sceaux: Gabay 1991. ISBN 2-87647-083-7
[Gtzl 2006] Gtzl, Dieter: Besondere Linien im Dreieck – eine Verallgemeinerung. MNU Der mathematische und naturwissenschaftliche Unterricht. 59/8 (1. 12. 2006), S. 468-471, ISSN 0025-5866
[Hauptmann 1995] Hauptmann, W.: Erzeugung ãmerkwrdiger PunkteÒ. PM Praxis der Mathematik 37, 1995, S. 8
[Hoehn 2001] Hoehn, Larry: Extriangles and Excevians. Mathematics Magazine, Vol. 74, No. 5, December 2001, p. 384-388
[Jacobi 1825] Jacobi, C. F. A.: De triangulorum rectilineorum proprietatibus quibusdam nondum satis cognitis. Naumburg 1825
[Kimberling 1998] Kimberling, Clark: Triangle Centers and Central Triangles. Congr. Numer. 129 (1998), p. 1 – 295
[Klemenz 2003] Klemenz, Heinz: Merkwrdiges im Dreieck. VSMP Bulletin, herausgegeben vom Verein Schweizerischer Mathematik- und Physiklehrer, No 91, Februar 2003, S. 16-23
[Walser 1990-1994] Walser, Hans: Schlu§punkt. Didaktik der Mathematik, 18 (1990) bis 22 (1994), jeweils letzte Heftseite
[Walser 1993] Walser, Hans: Die Eulersche Gerade als Ort "merkwrdiger Punkte". Didaktik der Mathematik (21), 1993, 95-98
[Walser 1994] Walser, Hans: Eine Verallgemeinerung der Winkelhalbierenden. Didaktik der Mathematik (22), 1994, S. 50-56
[Walser 2000] Walser, Hans: Lattice Geometry and Pythagorean Triangles. ZDM Zentralblatt fr Didaktik der Mathematik. Jahrgang 32, April 2000, Heft 2, S. 32 - 35
[Walser 2003] Walser, Hans: Eine Schar von Schnittpunkten im Dreieck. Praxis der Mathematik (2/45), 2003, S. 66 - 68
[Walser 2004] Walser, Hans: 99 Schnittpunkte. Beispiele – Bilder – Beweise. Edition am Gutenbergplatz, Leipzig 2004. ISBN 3-937219-10-2
[Walser 2006] 99 Points of Intersection. Examples
– Pictures – Proofs. Translated by Peter Hilton and Jean Pedersen.
The Mathematical Association of America 2006. ISBN 0-88385-553-4
[Walser 2009] Walser, Hans: Der Goldene Schnitt. 5., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig 2009. ISBN 978-3-937219-98-1
[Wildberger
2010] Wildberger,
Norman J.: Chromogeometry. The Mathematical Intelligencer. Volume 32, Number 1, 2010.
Springer. p. 26-32
Letzte nderung 2. Juli 2010