Hans Walser

Schnittpunkte 401-500

Die Bildsequenzen sind im Sinne einer „minimal art“ als Bilder ohne Worte konzipiert. Dabei wurde folgende grafische Systematik verwendet:

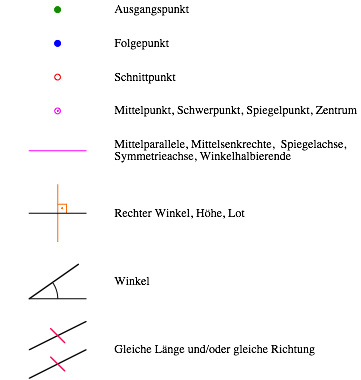
Die drei kleinen Bilder im Querstreifen deuten die Entstehung der Gesamtfigur an.

Gegebenenfalls finden sich unterhalb der Figur Literaturangaben oder Hinweise auf Anregungen, die zu diesen Figuren geführt haben.

Schnittpunkt 401

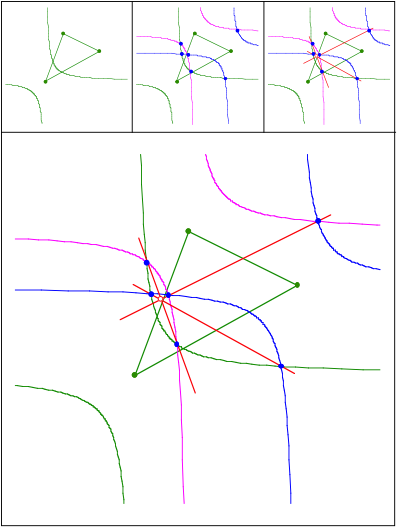
Verschobene gleichseitige Hyperbeln. Vgl. [Wildberger 2010]

Schnittpunkt 402

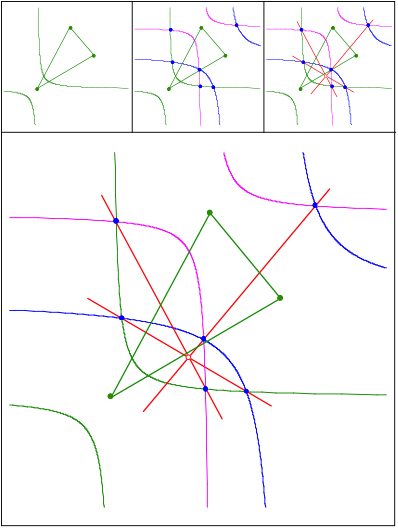
Verschieden große Hyperbeln

Schnittpunkt 403

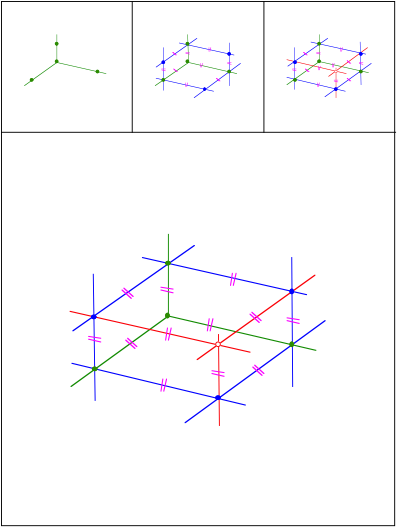
Ergänzung zum Quader

Schnittpunkt 404

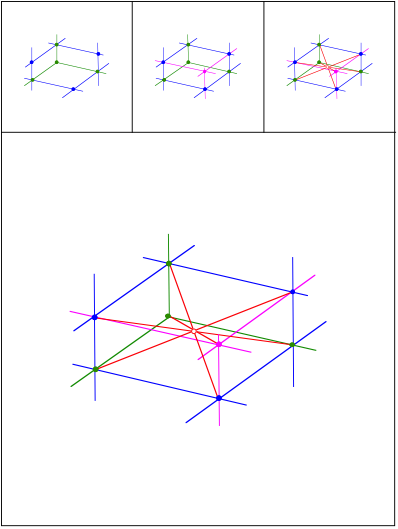
Raumdiagonalen im Quader

Schnittpunkt 405

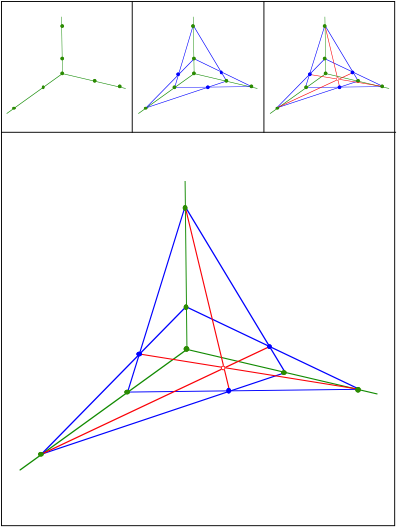
Ergänzung zum Quader in Perspektive

Schnittpunkt 406

Raumdiagonalen

Schnittpunkt 407

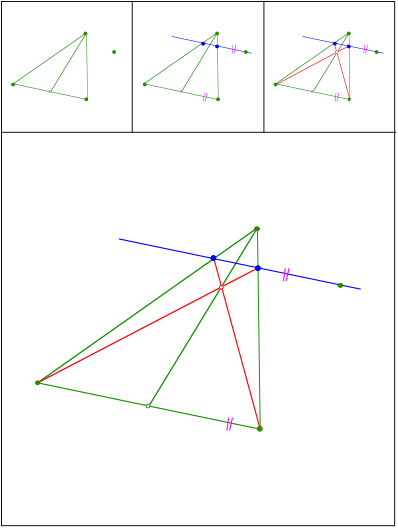
Schnittpunkt 408

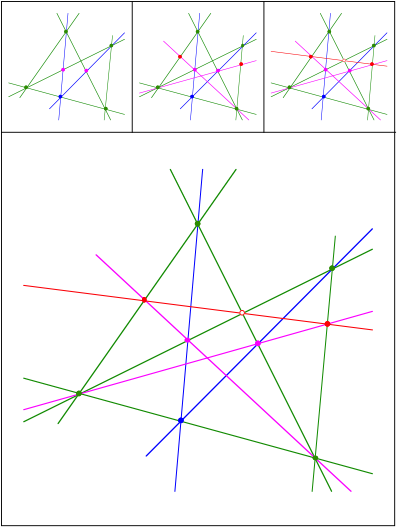
Schnittpunkt 409

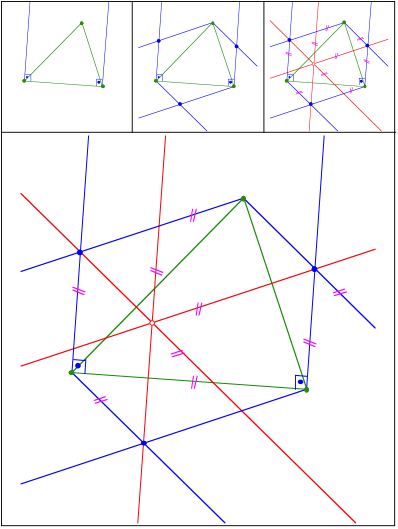
Schnittpunkt 410

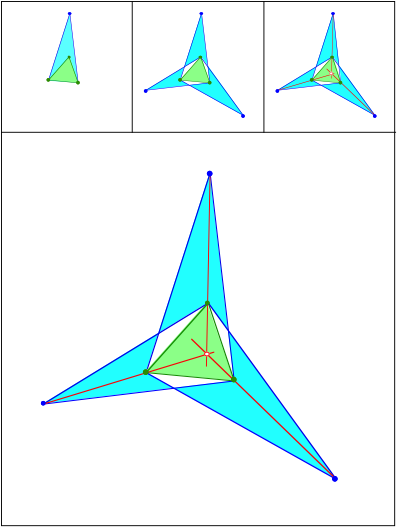
Ähnliche gleichschenklige Dreiecke (Kiepert)

Schnittpunkt 411

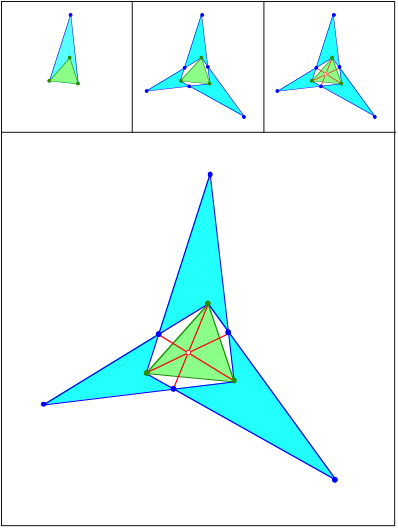
Ähnliche gleichschenklige Dreiecke

Schnittpunkt 412

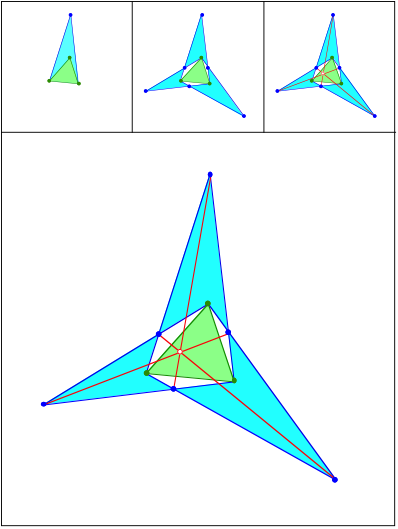
Ähnliche gleichschenklige Dreiecke

Schnittpunkt 413

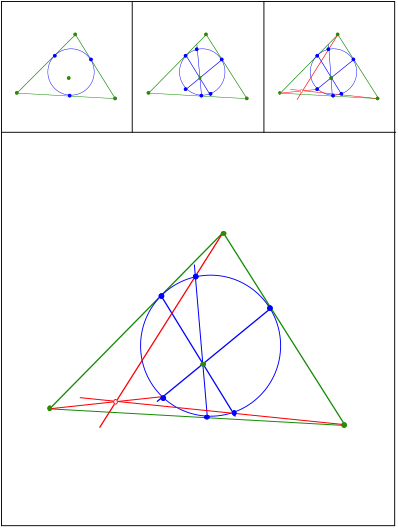
Rabinowitz

Schnittpunkt 414

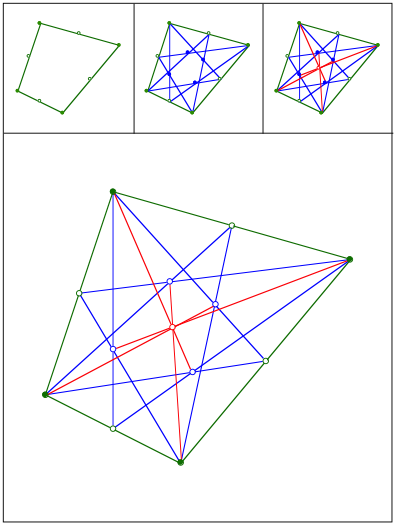
Eckenschwerpunkt

Schnittpunkt 415

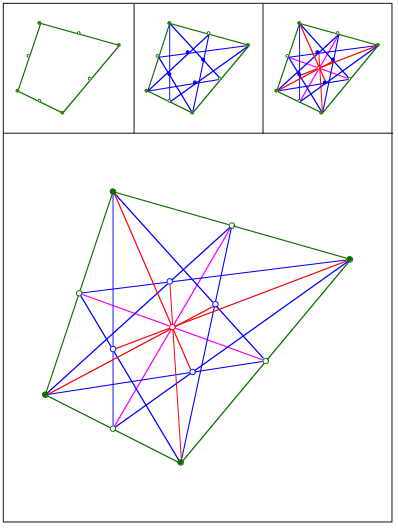
Eckenschwerpunkt

Schnittpunkt 416

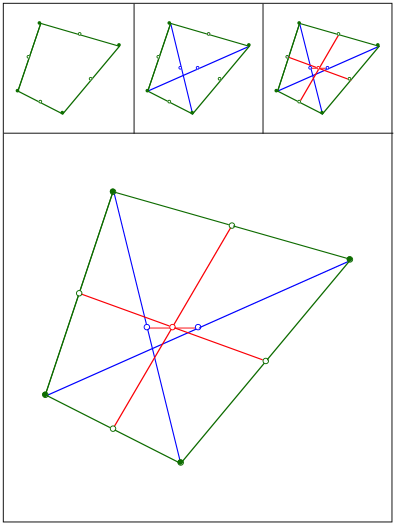
Eckenschwerpunkt

Schnittpunkt 417

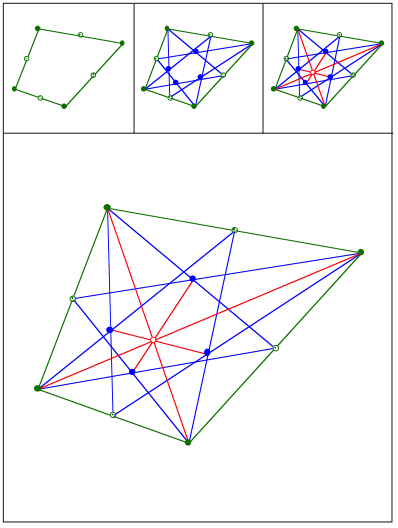
Schnittpunkt 418

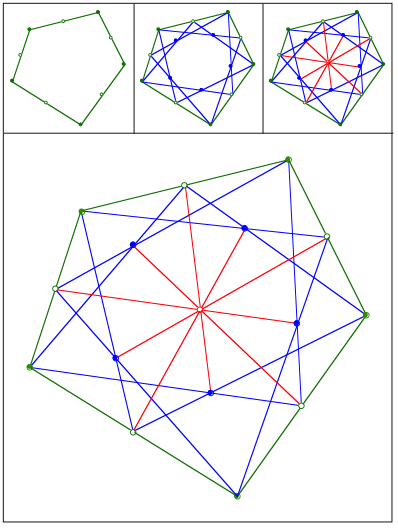
Eckenschwerpunkt

Schnittpunkt 419

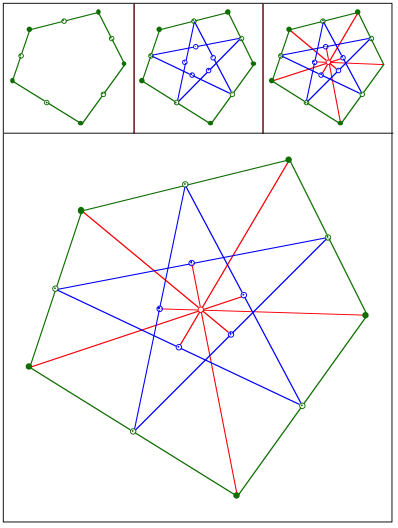
Eckenschwerpunkt

Schnittpunkt 420

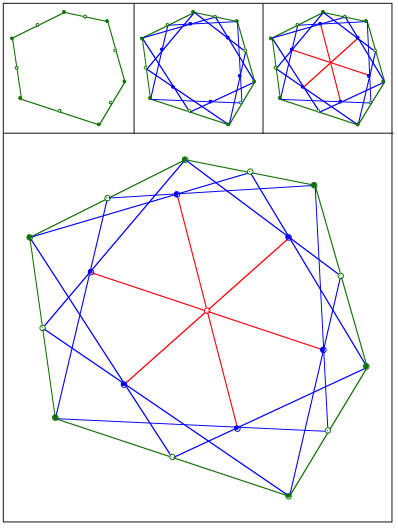
Eckenschwerpunkt. Das Sechseck mit den blauen Eckpunkten ist affin regulär.

Schnittpunkt 421

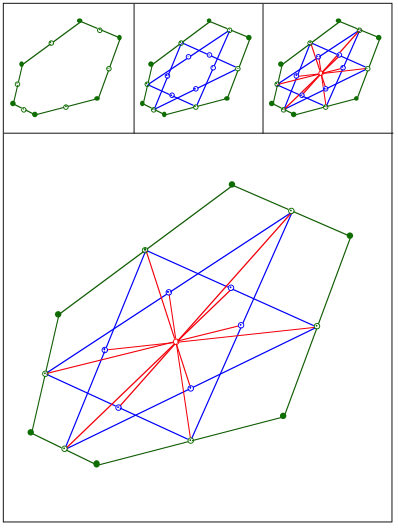
Eckenschwerpunkt

Schnittpunkt 422

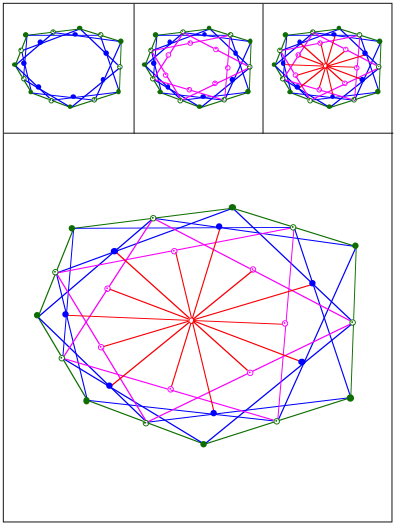
Eckenschwerpunkt

Schnittpunkt 423

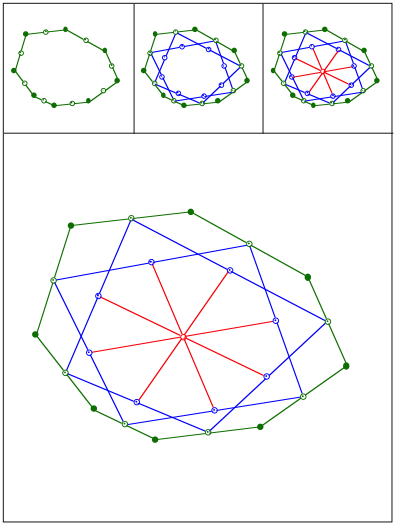
Eckenschwerpunkt

Schnittpunkt 424

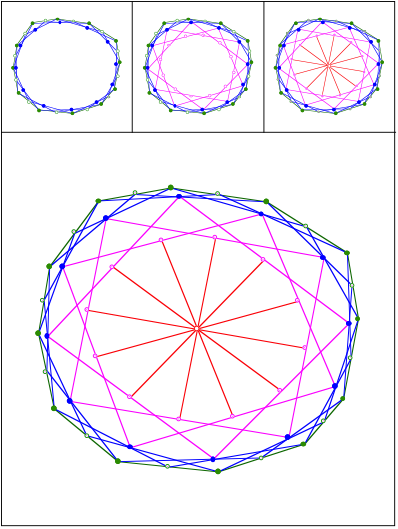
Eckenschwerpunkt

Schnittpunkt 425

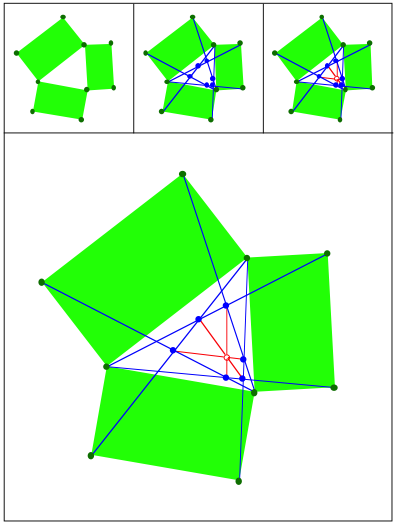
Ähnliche Rechtecke

Schnittpunkt 426

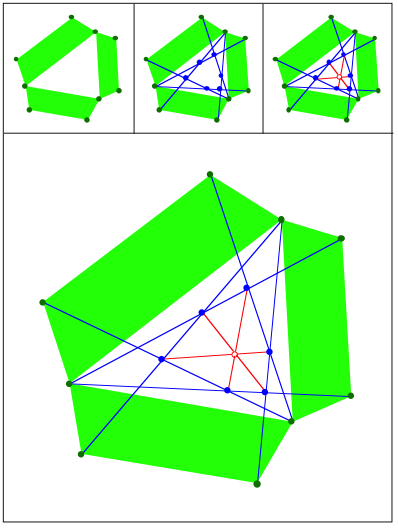
Ähnliche gleichschenklige Trapeze

Schnittpunkt 427

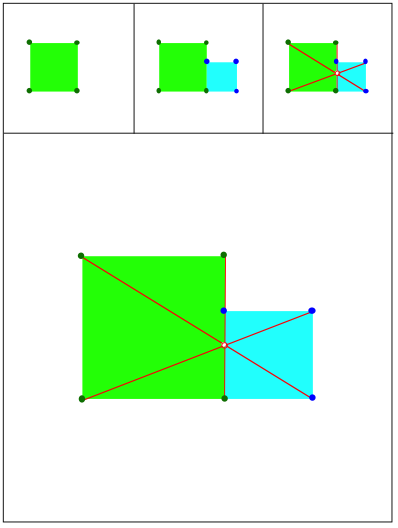
Schnittpunkt 428

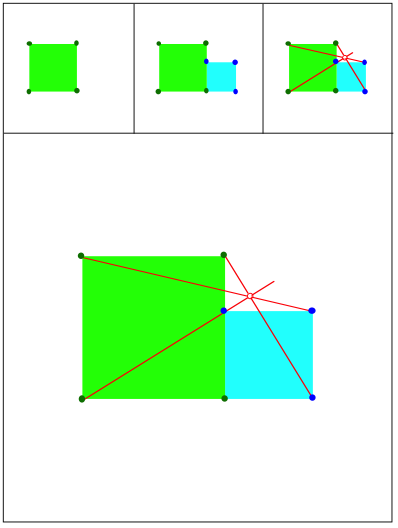
Schnittpunkt 429

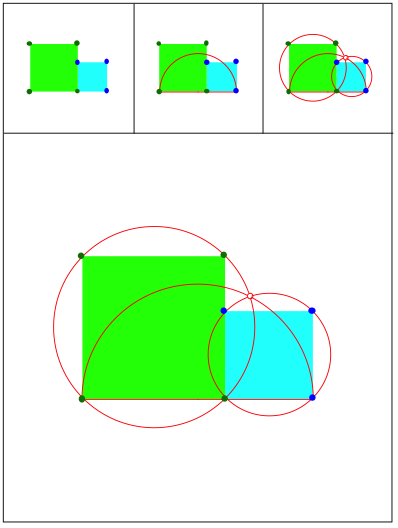
Thaleskreis und Umkreise

Schnittpunkt 430

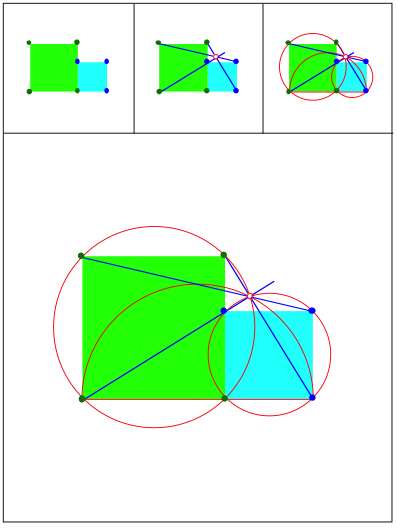
Schnittpunkt 431

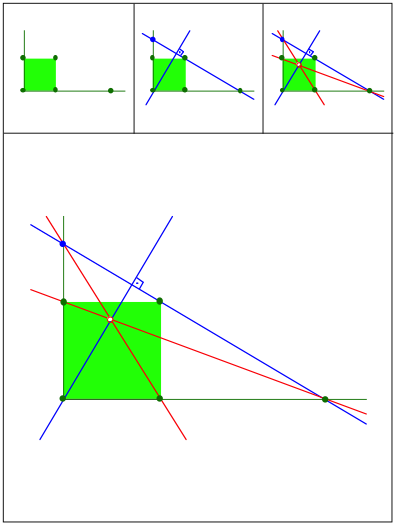
Schnittpunkt 432

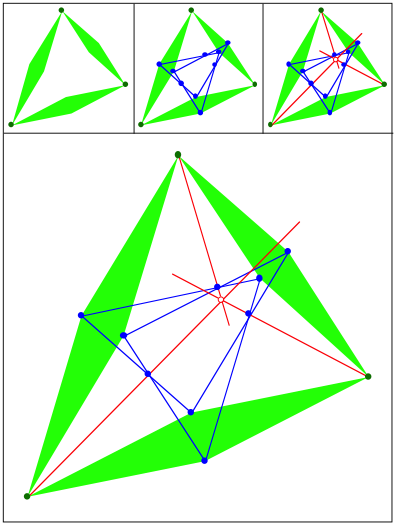
Ähnliche Rhomben

Schnittpunkt 433

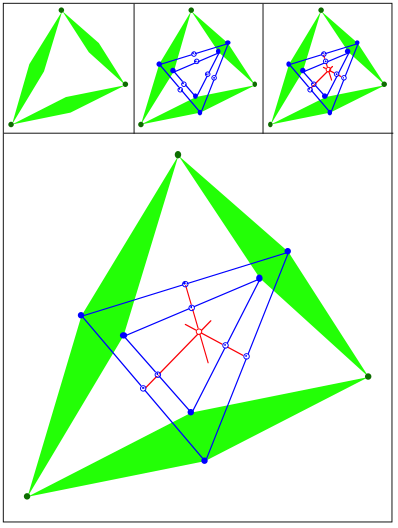
Schnittpunkt 434

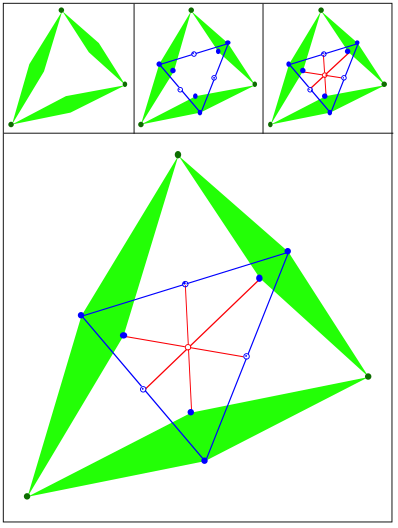
Schnittpunkt 435

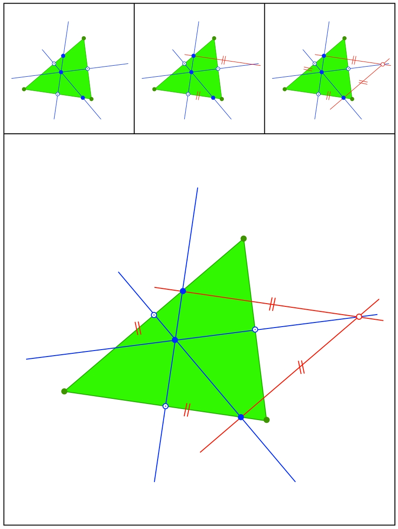
Parallelogramm

Schnittpunkt 436

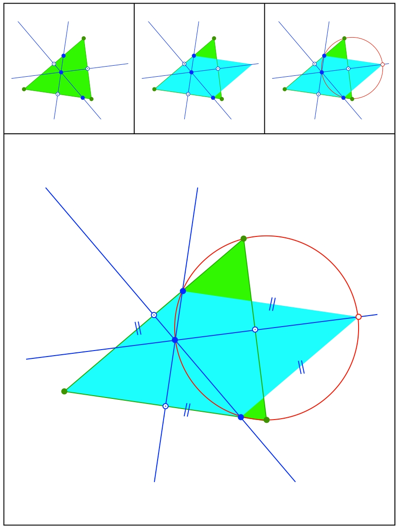
Parallelogramm

Schnittpunkt 437

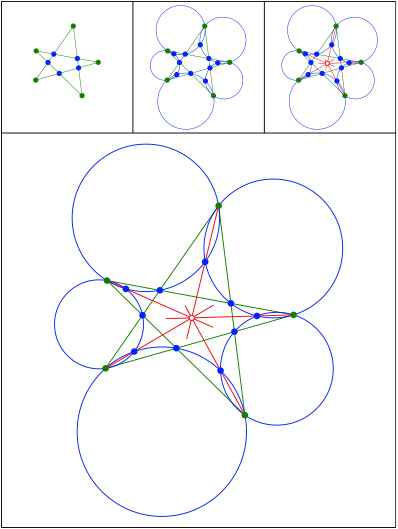
Idea: J. Chris Fisher, Larry Hoehn, and Eberhard M. Schröder

Schnittpunkt 438

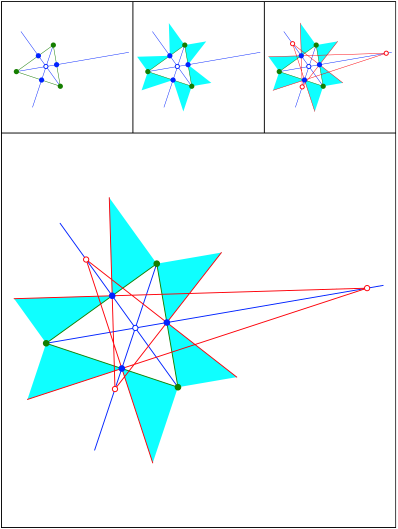
Höhen

Schnittpunkt 439

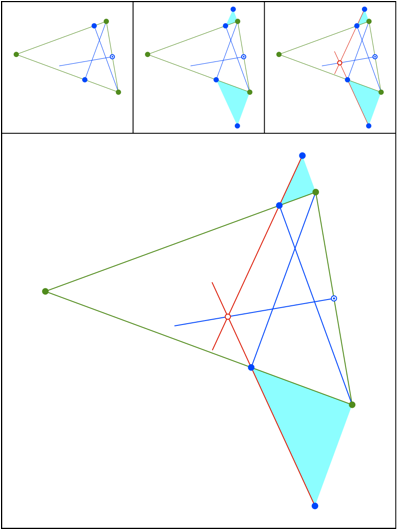
Höhen und eine Mittelsenkrechte

Schnittpunkt 440

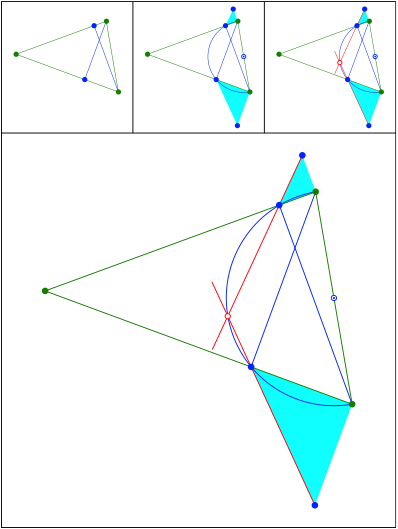
Höhen und Thaleskreis

Schnittpunkt 441

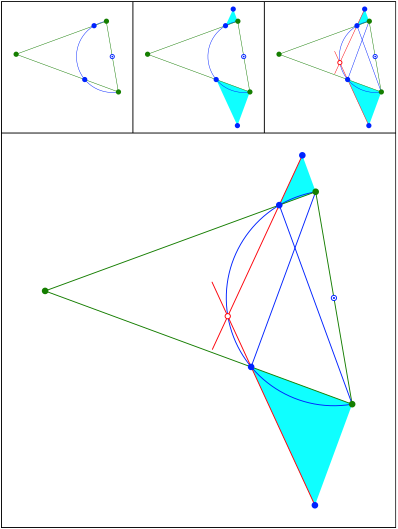
Schnittpunkt 442

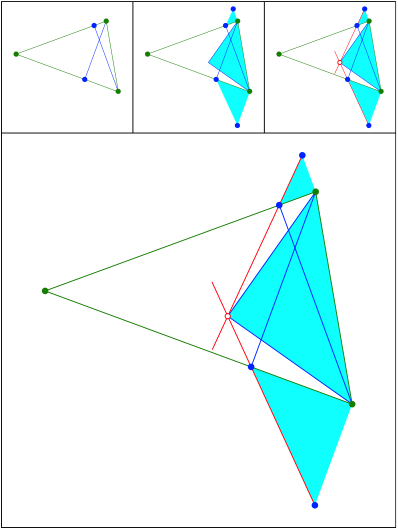
Schnittpunkt 443

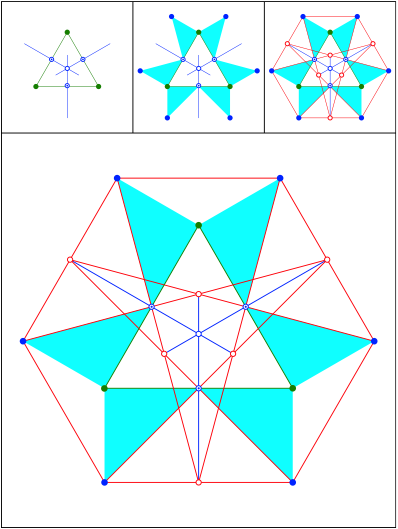
Schnittpunkt 444

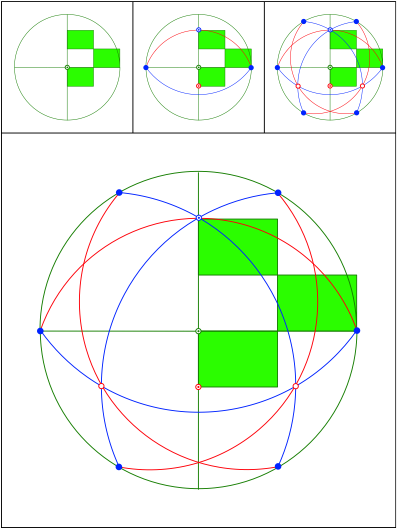
Rechtecke im DIN-Format

Schnittpunkt 445

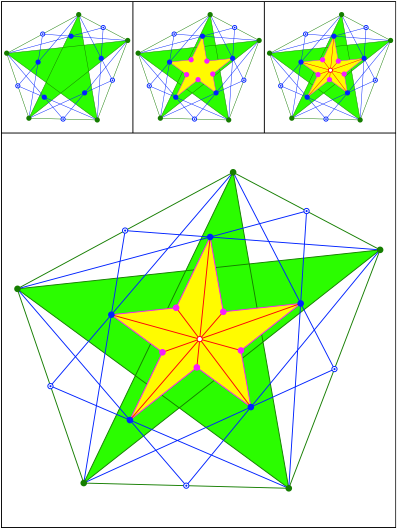
Flächenschwerpunkt

Schnittpunkt 446

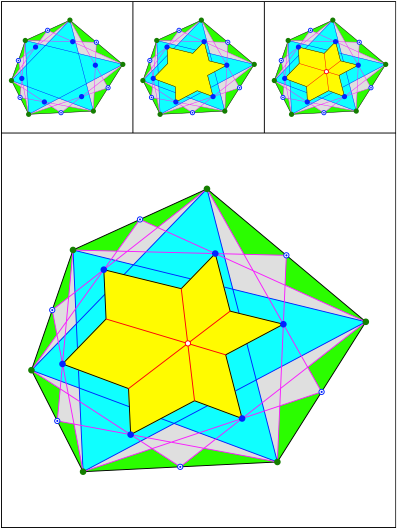
Schnittpunkt 447

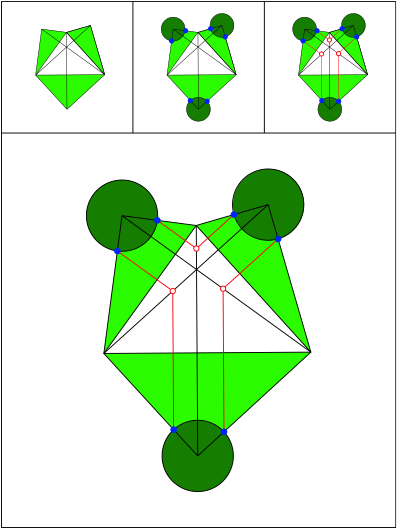
Schnittpunkt 448

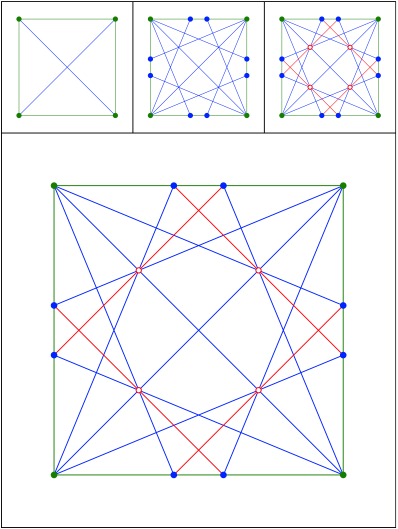
Winkelhalbierende

Schnittpunkt 449

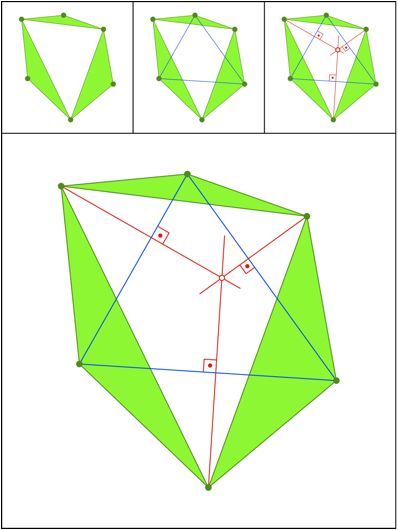
Gleichschenklige Dreiecke. Hintergrund: Potenzgeraden

Schnittpunkt 450

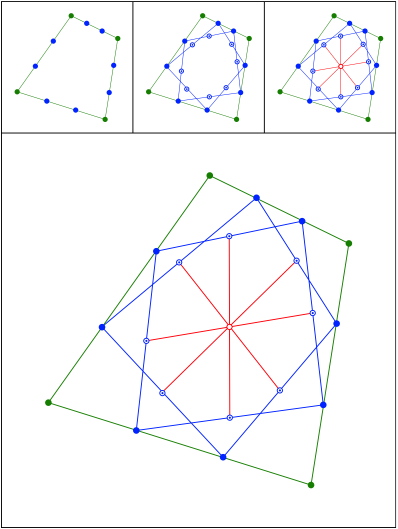
Dritteln und Halbieren

Schnittpunkt 451

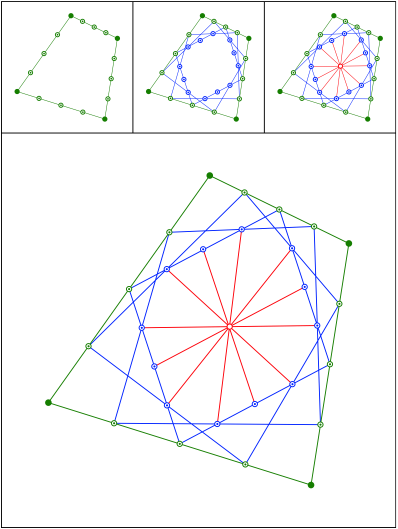
Halbieren und Vierteln

Schnittpunkt 452

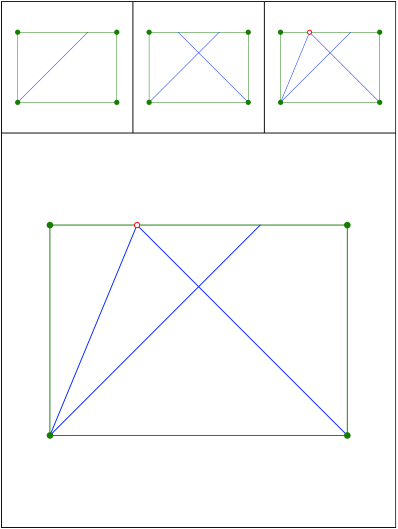
Winkelhalbierende im DIN-Rechteck

Schnittpunkt 453

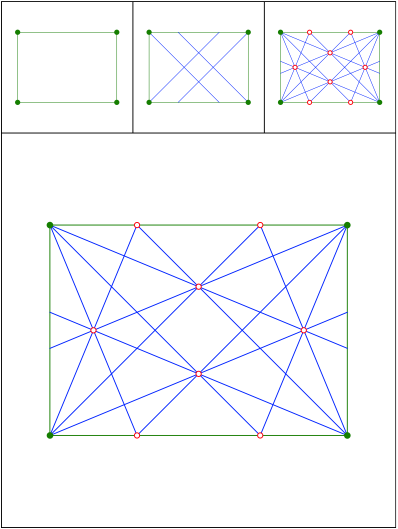
Winkelhalbierende im DIN-Rechteck

Schnittpunkt 454

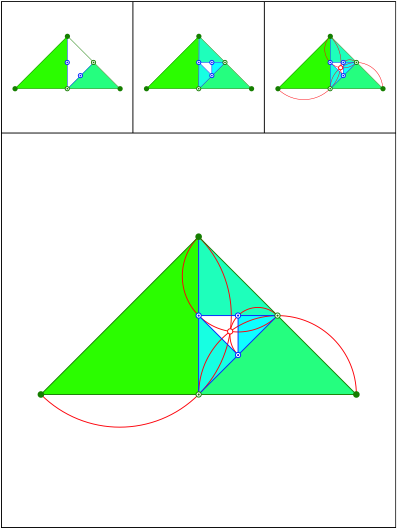
Rechtwinklig gleichschenklige Dreiecke. Thaleskreise

Schnittpunkt 455

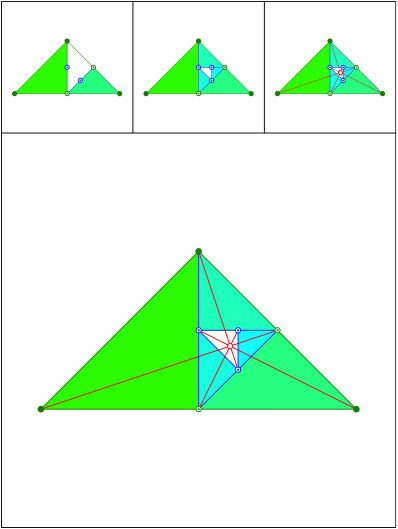
Rechtwinklig gleichschenklige Dreiecke

Schnittpunkt 456

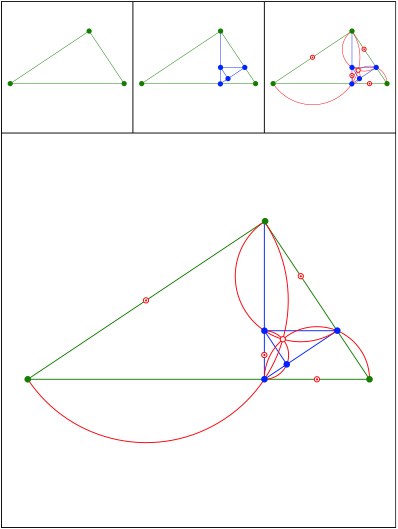
Rechtwinklige Dreiecke und Thaleskreise

Schnittpunkt 457

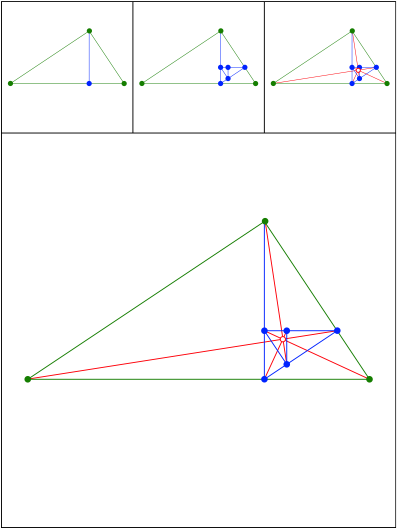
Rechtwinklige Dreiecke

Schnittpunkt 458

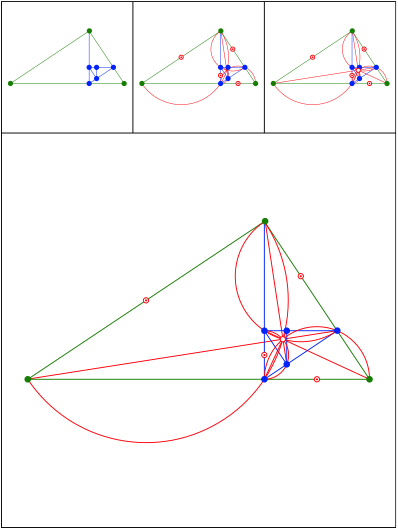
Rechtwinklige Dreiecke

Schnittpunkt 459

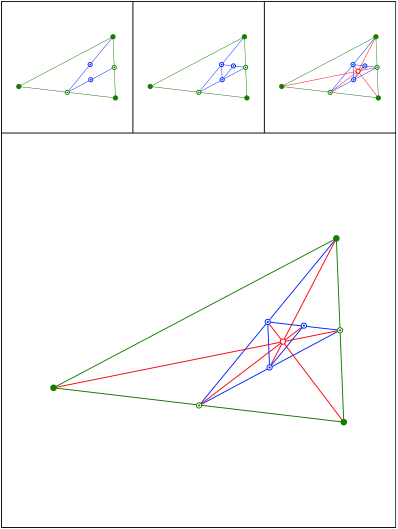
Schnittpunkt 460

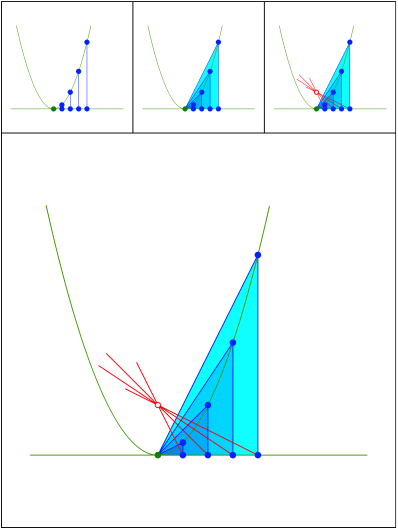
Dreieckshöhen. Wo ist der Brennpunkt der Parabel?

Schnittpunkt 461

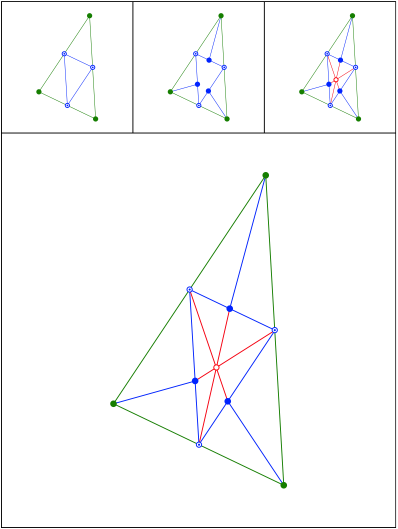
Mittendreieck und Winkelhalbierende

Schnittpunkt 462

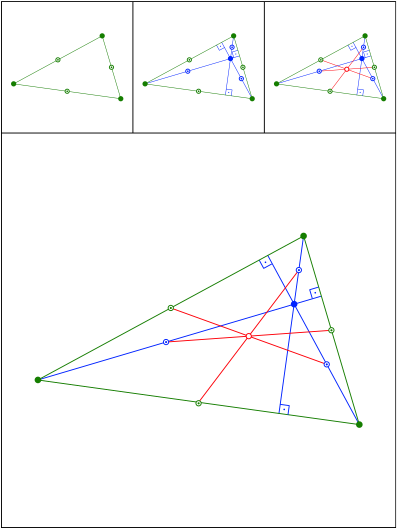
Feuerbach

Schnittpunkt 463

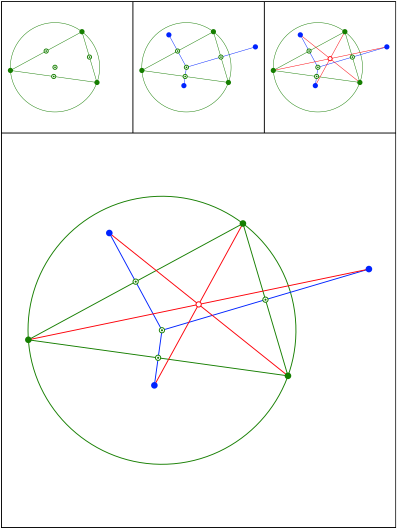
Schnittpunkt 464

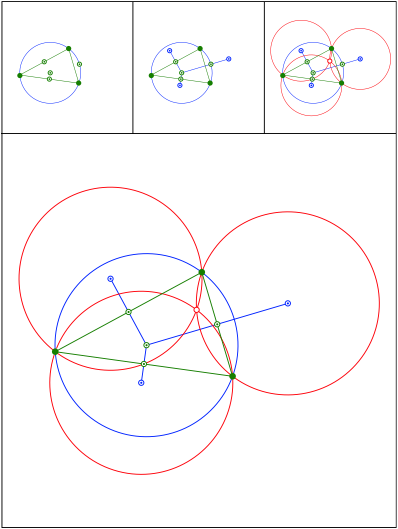
Schnittpunkt 465

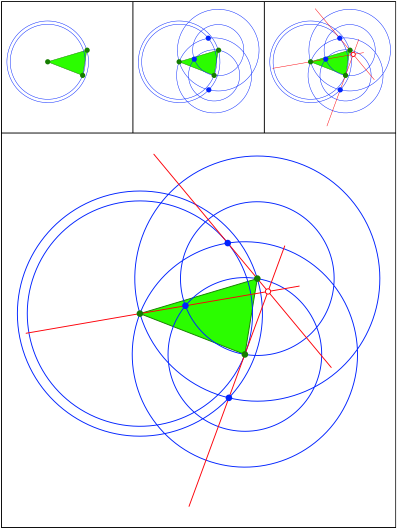
Anregung: Johanna Heitzer. Äußerer Fermat-Punkt

Schnittpunkt 466

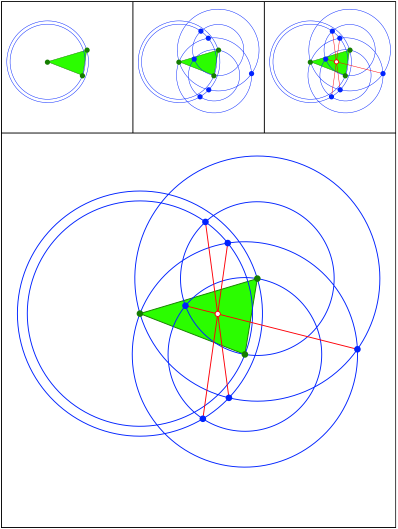
Anregung: Johanna Heitzer

Schnittpunkt 467

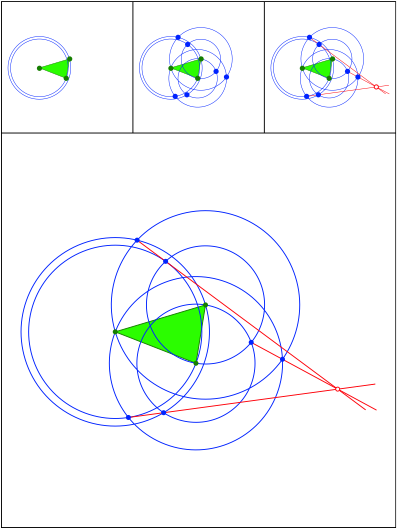
Anregung: Johanna Heitzer

Schnittpunkt 468

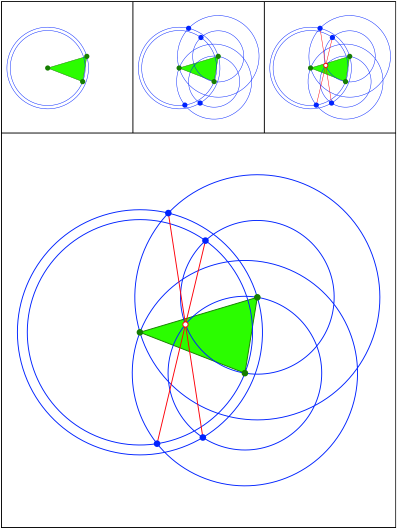
Anregung: Johanna Heitzer

Schnittpunkt 469

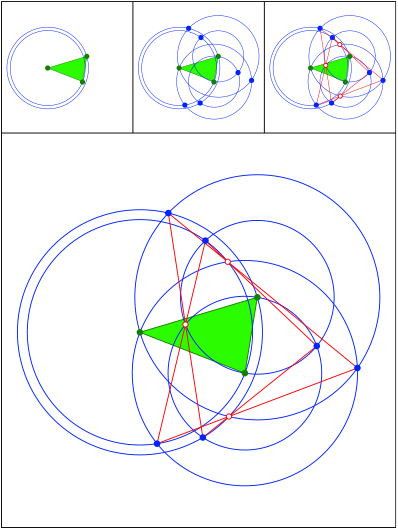
Anregung: Johanna Heitzer

Schnittpunkt 470

Inkreismittelpunkt

Schnittpunkt 471

Ankreismittelpunkt

Schnittpunkt 472

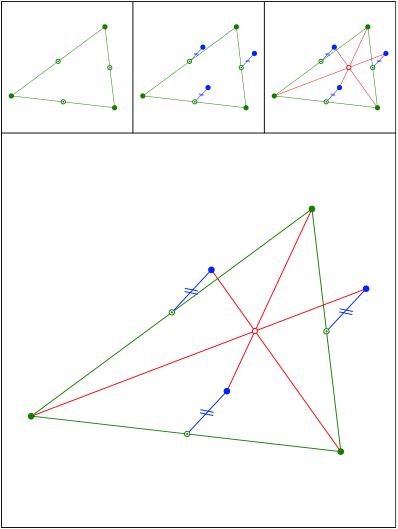
Schnittpunkt 473

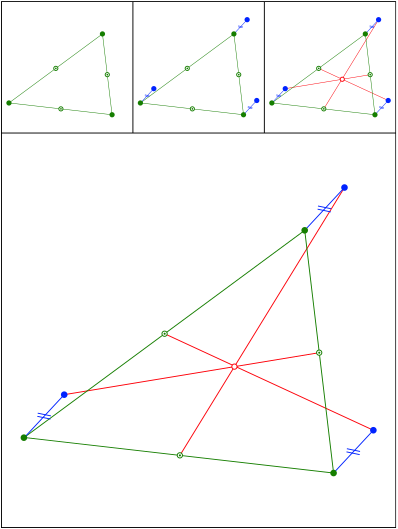
Schnittpunkt 474

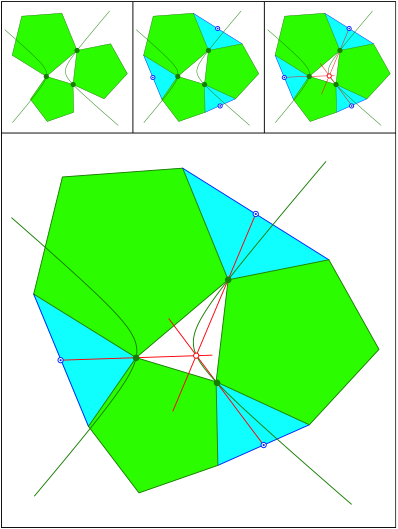
Punkt auf Kiepert-Hyperbel

Schnittpunkt 475

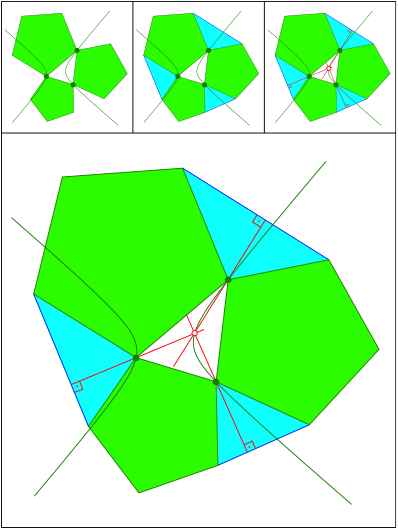
Punkt auf Kiepert-Hyperbel

Schnittpunkt 476

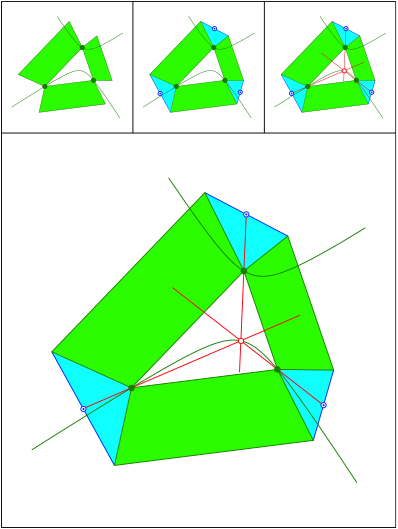
Gleichschenklige Trapeze. Punkt auf Kiepert-Hyperbel

Schnittpunkt 477

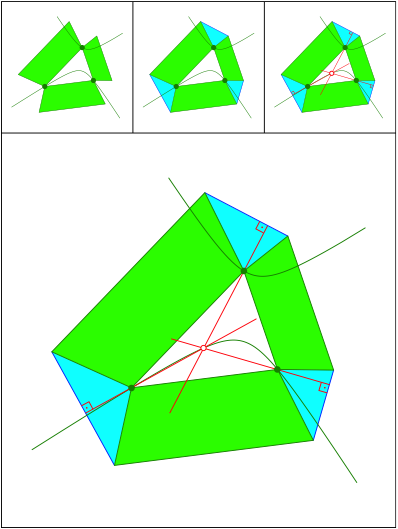
Gleichschenklige Trapeze. Punkt auf Kiepert-Hyperbel

Schnittpunkt 478

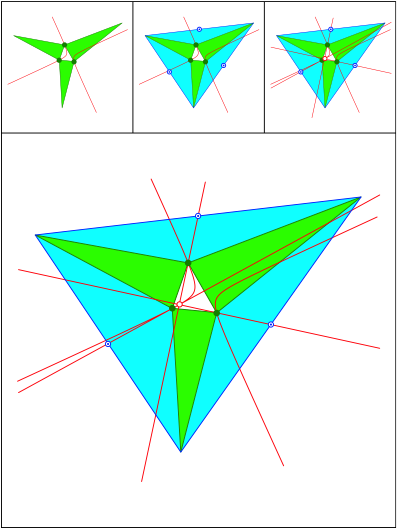
Gleichschenklige Dreiecke. Punkt auf Kiepert-Hyperbel

Schnittpunkt 479

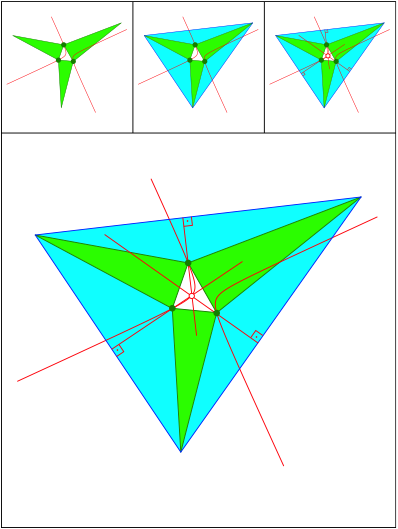
Gleichschenklige Dreiecke. Punkt auf Kiepert-Hyperbel

Schnittpunkt 480

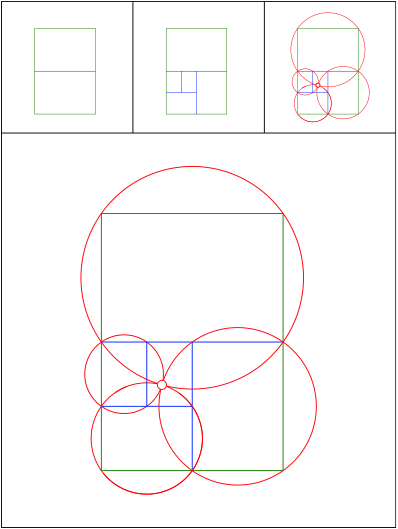
DIN-Format

Schnittpunkt 481

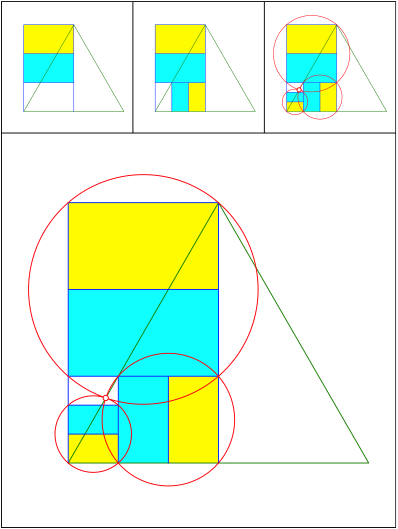
Schnittpunkt 482

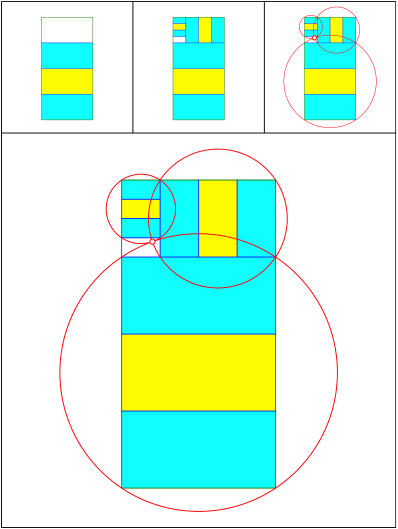
Schnittpunkt 483

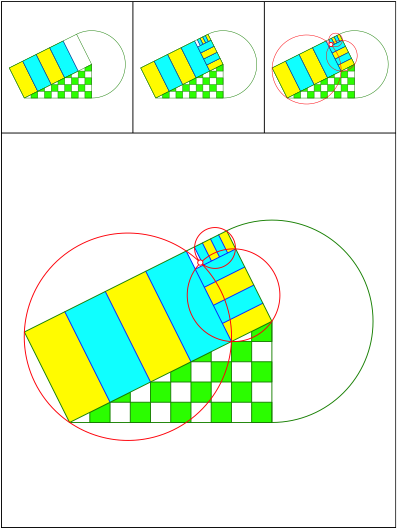
Schnittpunkt 484

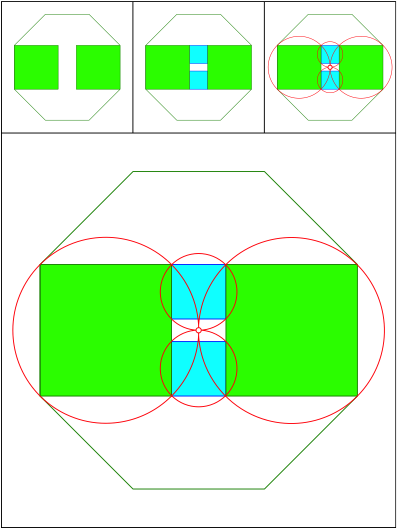
Schnittpunkt 485

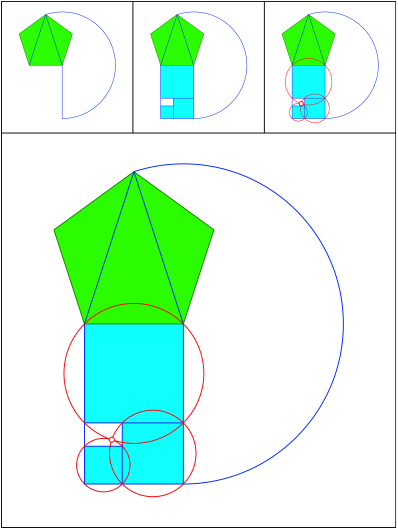
Schnittpunkt 486

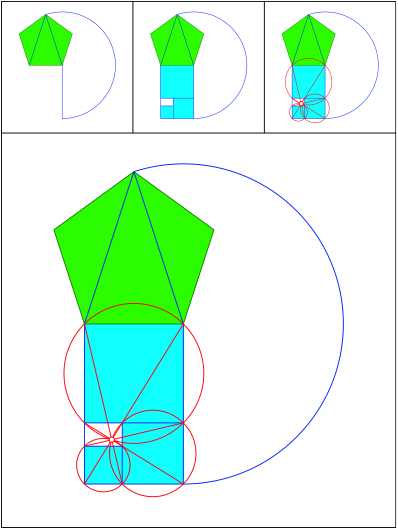
Schnittpunkt 487

Schnittpunkt 488

Schnittpunkt 489

Schnittpunkt 490

Schnittpunkt 491

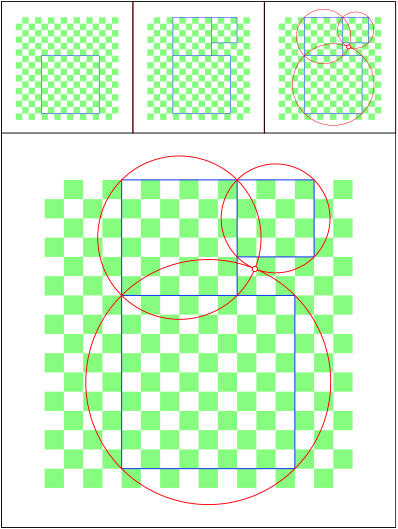
Schnittpunkt 492

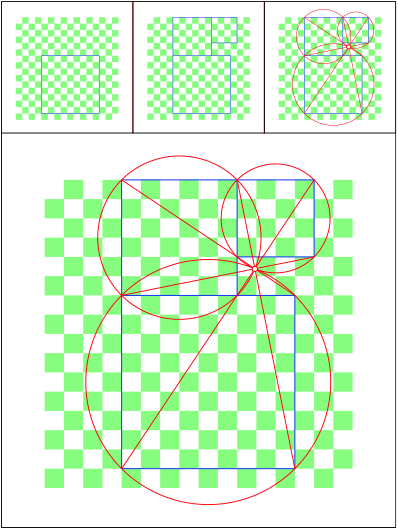
Schnittpunkt 493

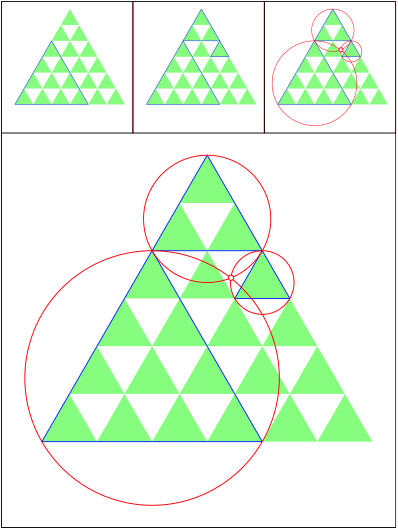
Schnittpunkt 494

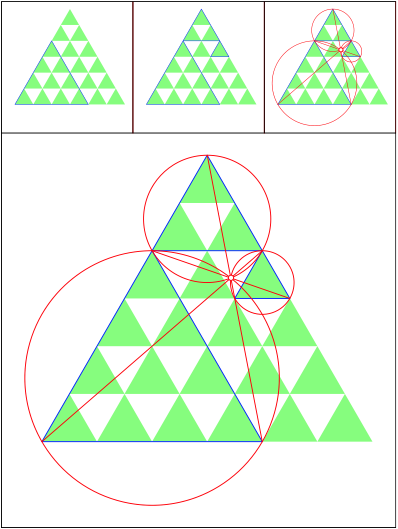
Schnittpunkt 495

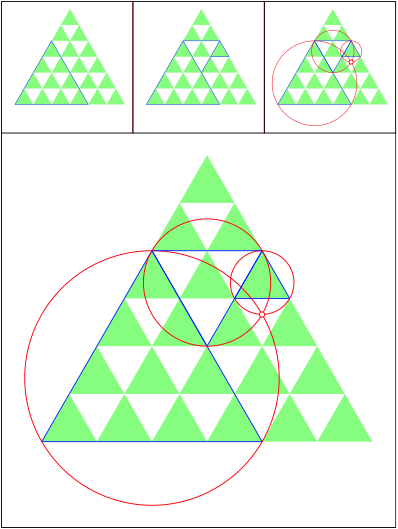
Schnittpunkt 496

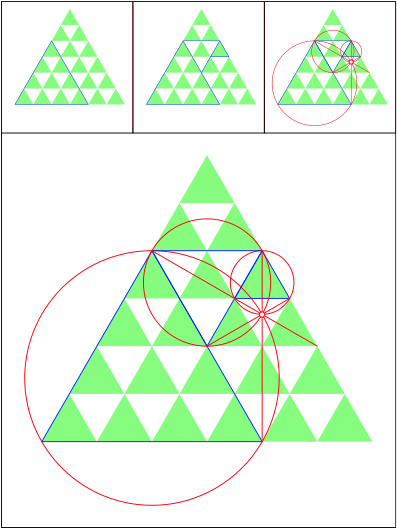
Schnittpunkt 497

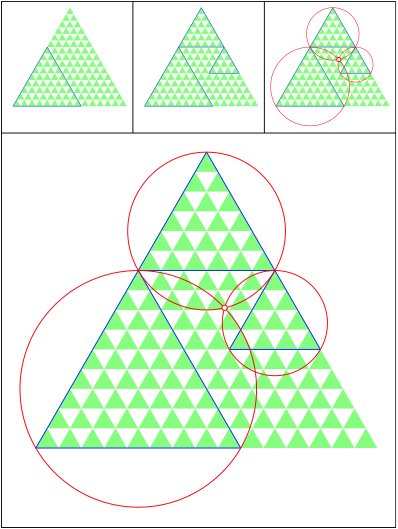
Schnittpunkt 498

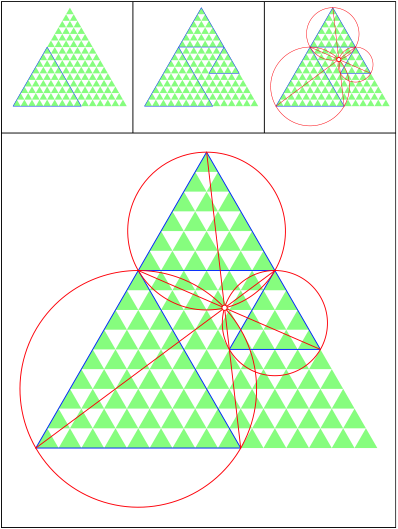
Schnittpunkt 499

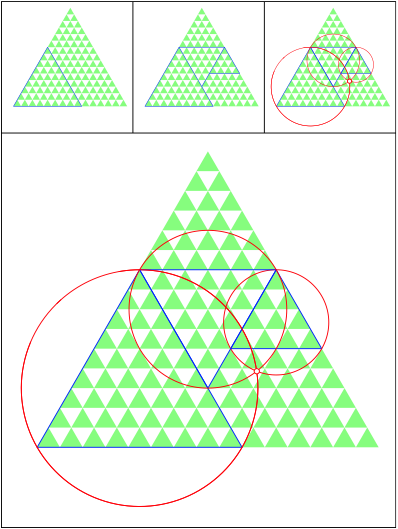
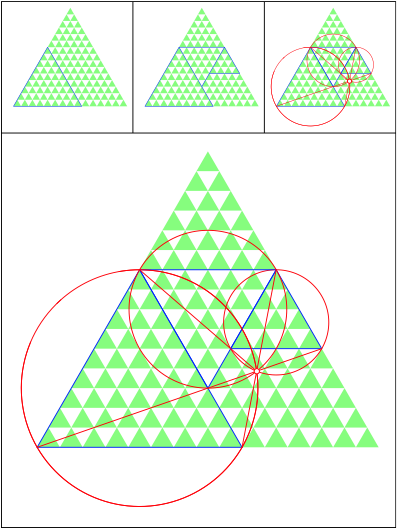
Schnittpunkt 500

Literatur

Baptist, Peter (1992): Die Entwicklung der neueren Dreiecksgeometrie. Mannheim: B.I.Wissenschaftsverlag. ISBN 3-411-15661-9

Donath, Emil (1976): Die merkwürdigen Punkte und Linien des ebenen Dreiecks. Berlin: Deutscher Verlag der Wissenschaften, 3. Auflage 1976.

Eddy, R.H. / Fritsch, R. (1994): The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June 1994, p. 188-205

Euklid (1980): Die Elemente. Nach Heibergs Text aus dem Griechischen übersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft. ISBN 3-534-01488-X

G.-M., F. (1920/1991): Exercices de Géométrie. Sixième édition. Tours - Paris: Mame - de Gigord 1920. Réimpression de la 6e édition publieé par Mame et De Gigord en 1920. Sceaux: Gabay 1991. ISBN 2-87647-083-7

Götzl, Dieter (2006): Besondere Linien im Dreieck – eine Verallgemeinerung. MNU Der mathematische und naturwissenschaftliche Unterricht. 59/8, S. 468-471, ISSN 0025-5866

Haag, Wilfried (2003): Wege zu geometrischen Sätzen. Stuttgart: Klett. ISBN 3-12-720120-6

Hauptmann, W. (1995): Erzeugung „merkwürdiger Punkte“. PM Praxis der Mathematik 37, S. 8

Hoehn, Larry (2001): Extriangles and Excevians. Mathematics Magazine, Vol. 74, No. 5, p. 384-388

Jacobi, C. F. A. (1825): De triangulorum rectilineorum proprietatibus quibusdam nondum satis cognitis. Naumburg.

Kimberling, Clark (1998): Triangle Centers and Central Triangles. Congr. Numer. 129, p. 1 – 295

Klemenz, Heinz (2003): Merkwürdiges im Dreieck. VSMP Bulletin, herausgegeben vom Verein Schweizerischer Mathematik- und Physiklehrer, No 91, S. 16-23

Walser, Hans (1990-1994): Schlußpunkt. Didaktik der Mathematik, 18 (1990) bis 22 (1994), jeweils letzte Heftseite

Walser, Hans (1993): Die Eulersche Gerade als Ort "merkwürdiger Punkte". Didaktik der Mathematik (21), 95-98

Walser, Hans (1994): Eine Verallgemeinerung der Winkelhalbierenden. Didaktik der Mathematik (22), S. 50-56

Walser, Hans (2000): Lattice Geometry and Pythagorean Triangles. ZDM Zentralblatt für Didaktik der Mathematik. Jahrgang 32, Heft 2, S. 32 - 35

Walser, Hans (2003): Eine Schar von Schnittpunkten im Dreieck. Praxis der Mathematik (2/45), S. 66 - 68

Walser, Hans (2006): 99 Points of Intersection. Examples – Pictures – Proofs. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America. ISBN 0-88385-553-4

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.

Wildberger, Norman J. (2010): Chromogeometry. The Mathematical Intelligencer. Volume 32, Number 1. Springer. p. 26-32

Letzte Änderung 24. Januar 2015