Hans Walser
Schnittpunkte 501 - 600
Die Bildsequenzen sind als Bilder ohne Worte konzipiert.
Farbreihenfolge: Dunkelgrn, blau, rot. Nach Bedarf werden auch andere Farben verwendet.
Die drei kleinen Bilder im Querstreifen deuten die Entstehung der Gesamtfigur an.
Gegebenenfalls finden sich unterhalb der Figur Literaturangaben oder Hinweise auf Anregungen, die zu diesen Figuren gefhrt haben.
Letzte nderung 17. Januar 2016
Schnittpunkt 501
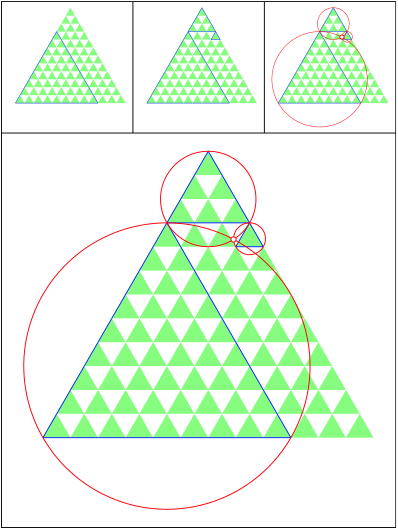
Schnittpunkt 502
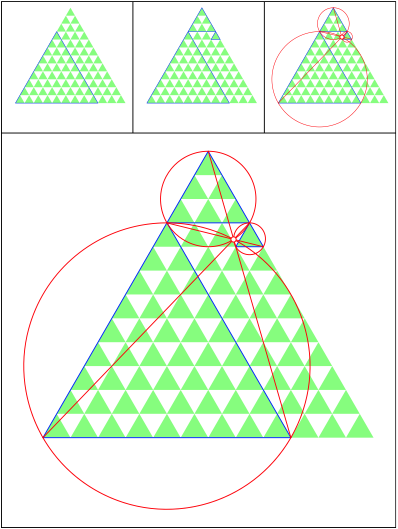
Schnittpunkt 503
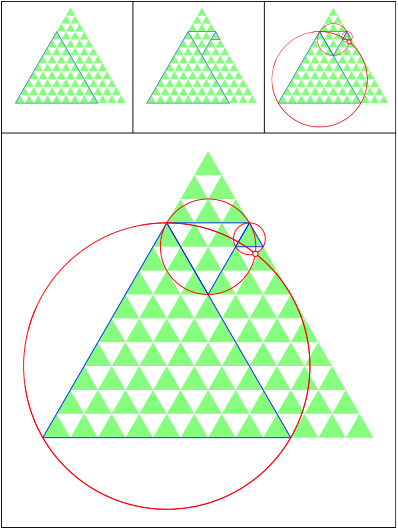
Schnittpunkt 504
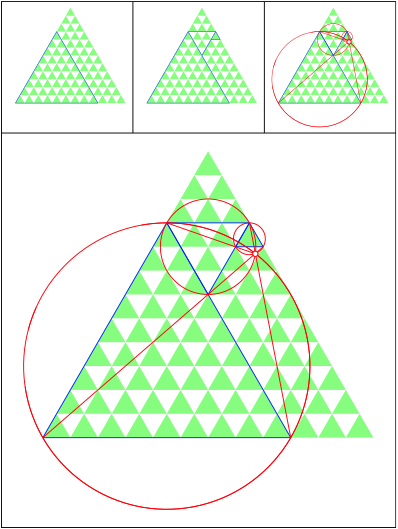
Schnittpunkt 505
Schnittpunkt 506
Schnittpunkt 507
Schnittpunkt 508
Schnittpunkt 509
Schnittpunkt 510
Schnittpunkt 511
Schnittpunkt 512
Schnittpunkt 513
Schnittpunkt 514
Schnittpunkt 515
Schnittpunkt 516
Schnittpunkt 517
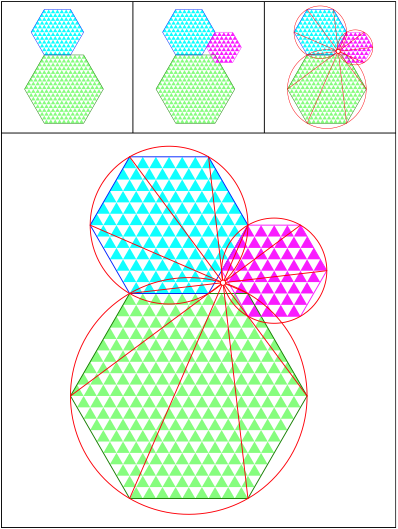
Schnittpunkt 518
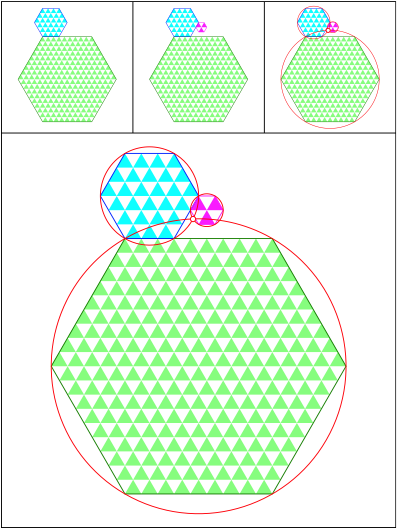
Schnittpunkt 519
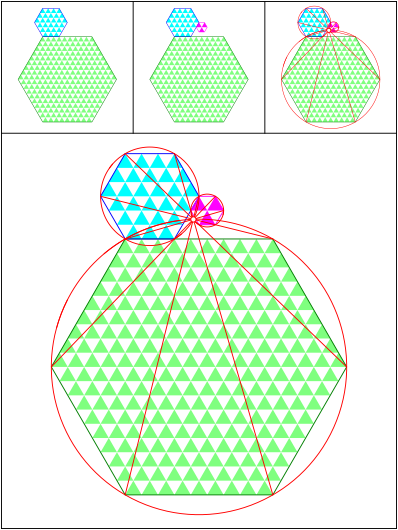
Schnittpunkt 520
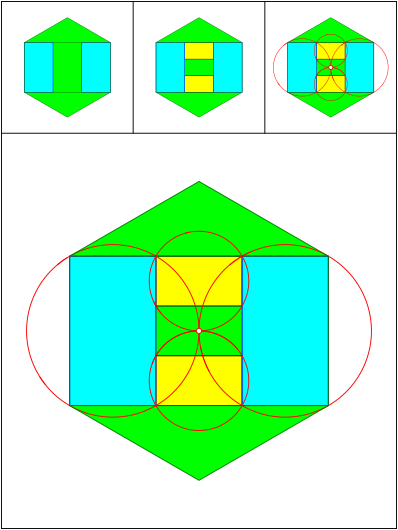
Schnittpunkt 521

Schnittpunkt 522
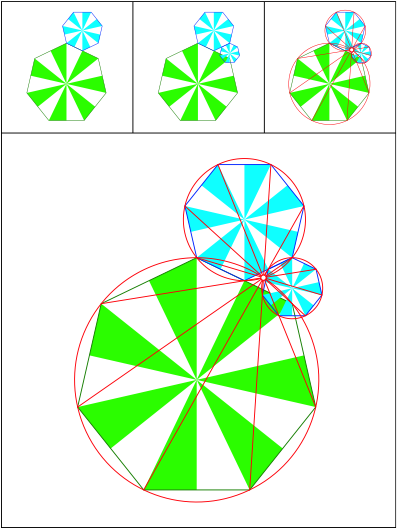
Schnittpunkt 523
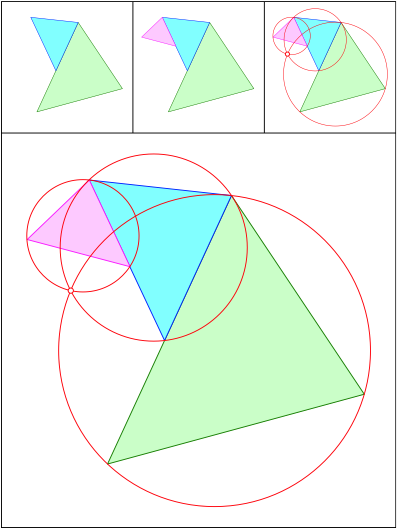
www.walser-h-m.ch/hans/Miniaturen/S/Schnittpunkt/Schnittpunkt.htm
Schnittpunkt 524
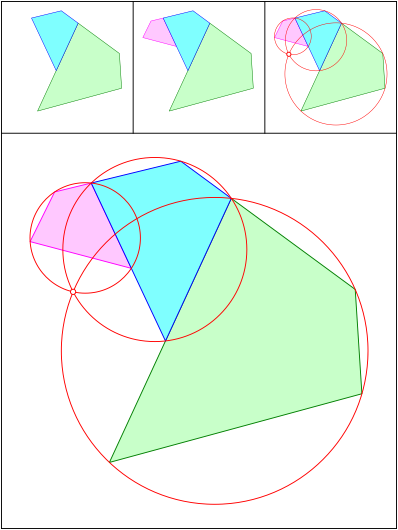
Schnittpunkt 525
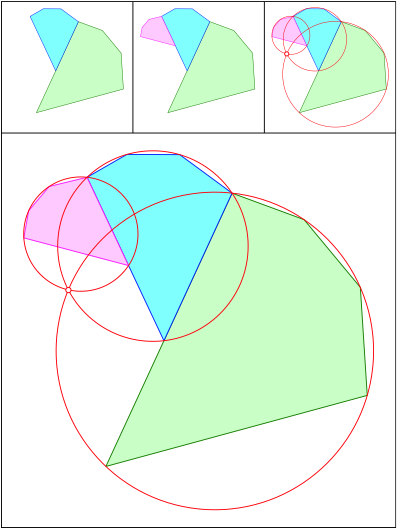
Schnittpunkt 526
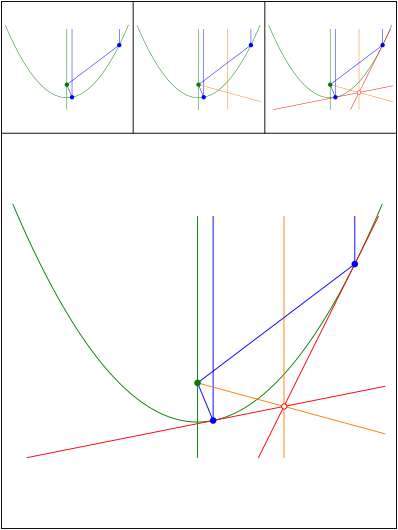
Winkelhalbierende, Mittelparallele und Tangenten
Schnittpunkt 527
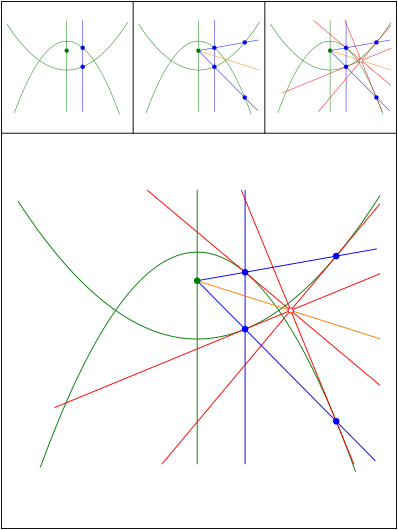
Konfokale Parabeln
Schnittpunkt 528
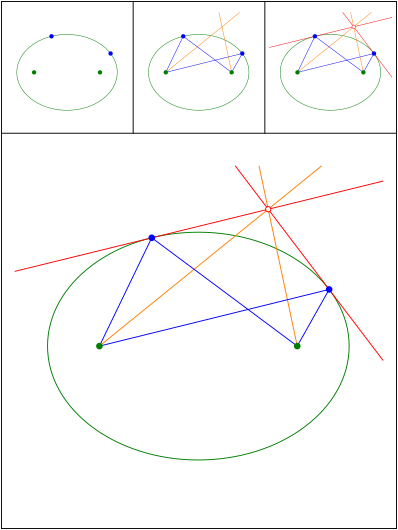
Winkelhalbierende und Tangenten
Schnittpunkt 529

Winkelhalbierende und Tangenten
Schnittpunkt 530
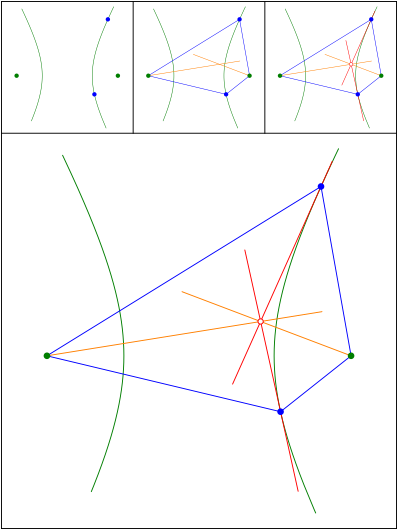
Winkelhalbierende und Tangenten
Schnittpunkt 531

Winkelhalbierende und Tangenten
Schnittpunkt 532
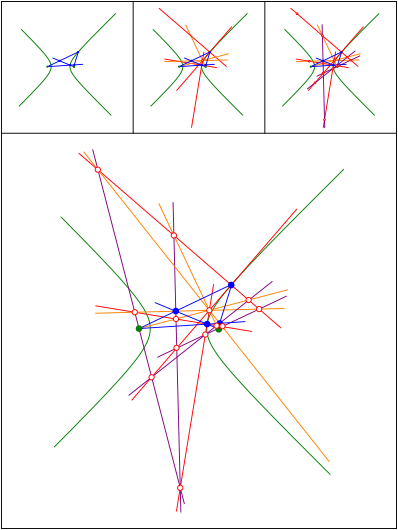
Tangenten, innere und u§ere Winkelhalbierende
Schnittpunkt 533
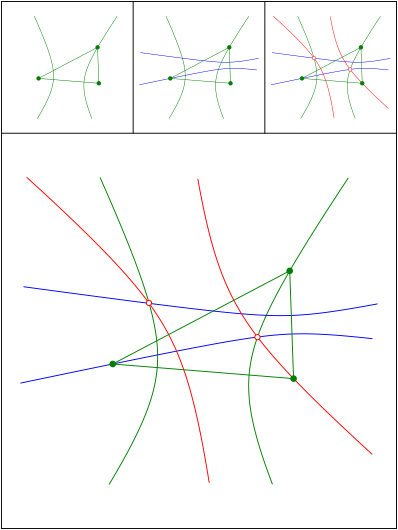
Hyperbeln im Dreieck
Schnittpunkt 534
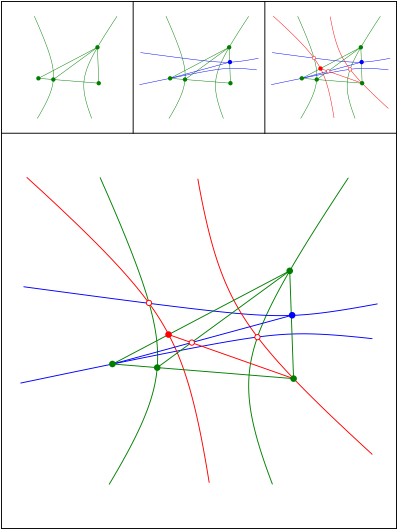
Nagel-Punkt
Schnittpunkt 535

Zwei Ellipsen und eine Hyperbel
Schnittpunkt 536

Schnittpunkt 537

Schnittpunkt 538

Schnittpunkt 539
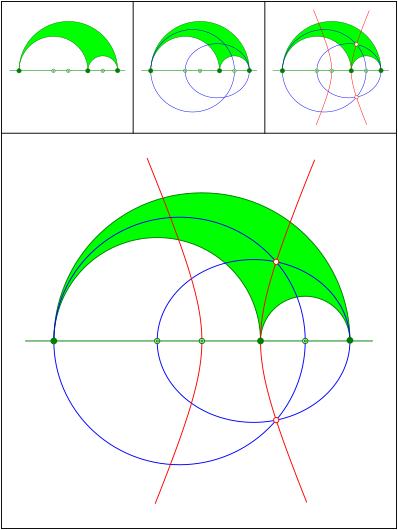
Kegelschnitte im Arbelos
Schnittpunkt 540

Schnittpunkt 541
Schnittpunkt 542
Schnittpunkt 543
Schnittpunkt 544
Schnittpunkt 545
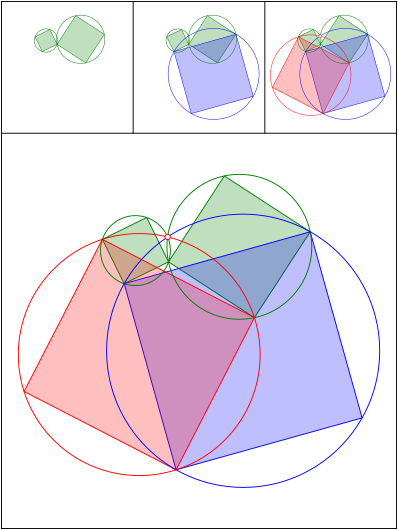
Schnittpunkt 546

Schnittpunkt 547

Schnittpunkt 548

Schnittpunkt 549

Schnittpunkt 550
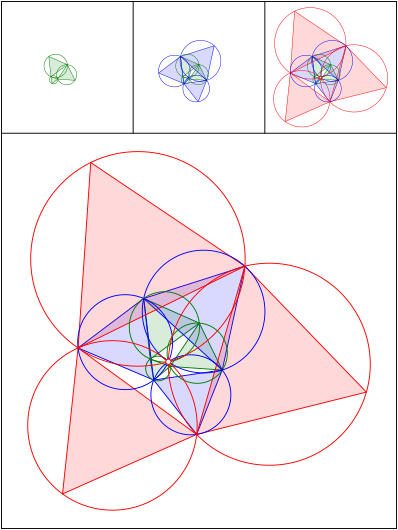
Schnittpunkt 551
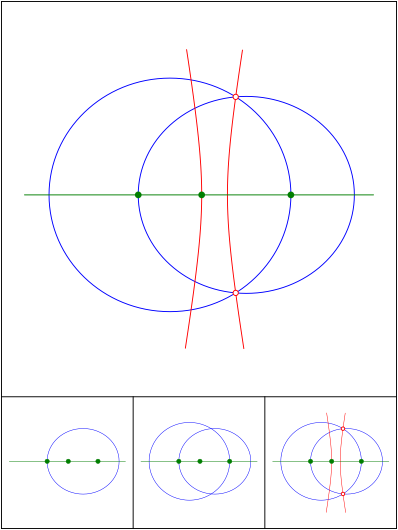
Zwei Ellipsen und eine Hyperbel
Schnittpunkt 552
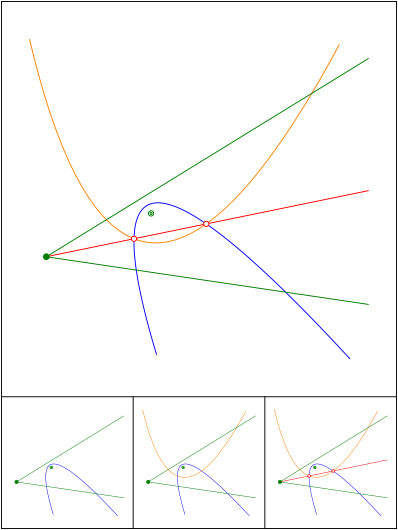
Zwei Parabeln und Winkelhalbierende
Schnittpunkt 553

Zwei Parabeln und u§ere Winkelhalbierende
Schnittpunkt 554

Drei Parabeln mit gemeinsamem Brennpunkt
Schnittpunkt 555
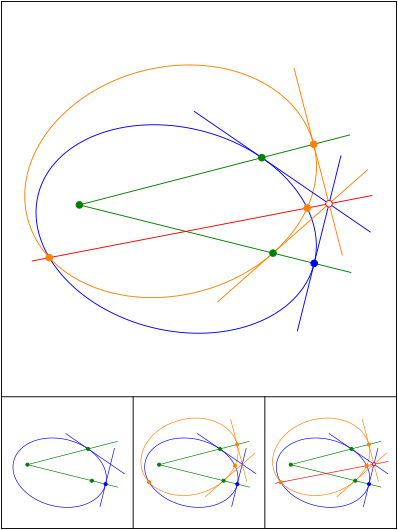
Schnittpunkt 556

Schnittpunkt 557

Schnittpunkt 558
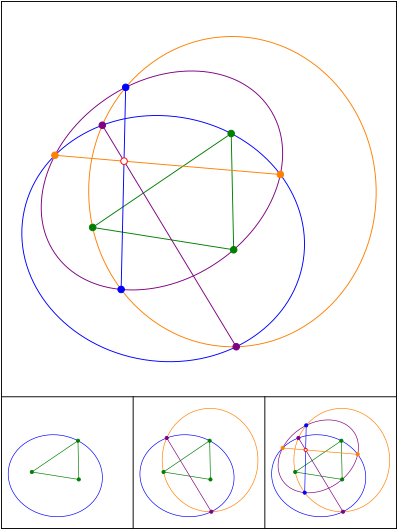
Drei Ellipsen
Schnittpunkt 559

Drei Ellipsen und Euler-Gerade
Schnittpunkt 560
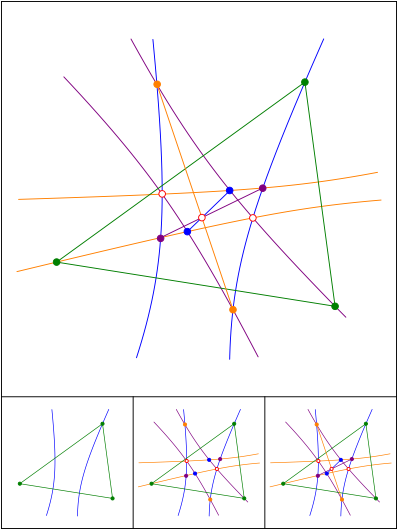
Drei Hyperbeln
Schnittpunkt 561
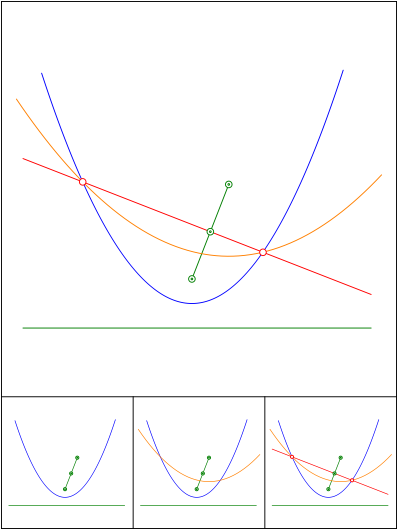
Schnittpunkt 562
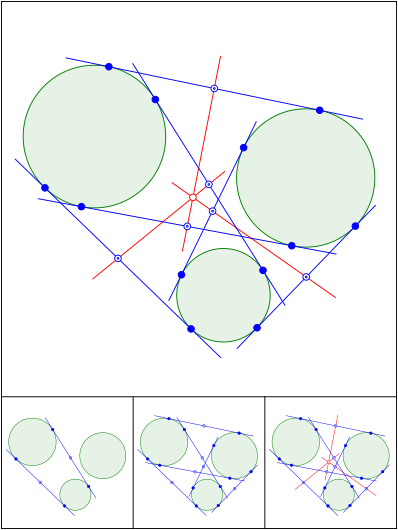
Schnittpunkt 563

Schnittpunkt 564

Schnittpunkt 565
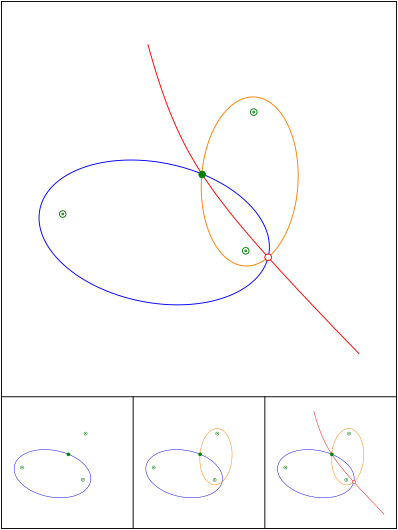
Zwei Ellipsen und eine Hyperbel
Schnittpunkt 566
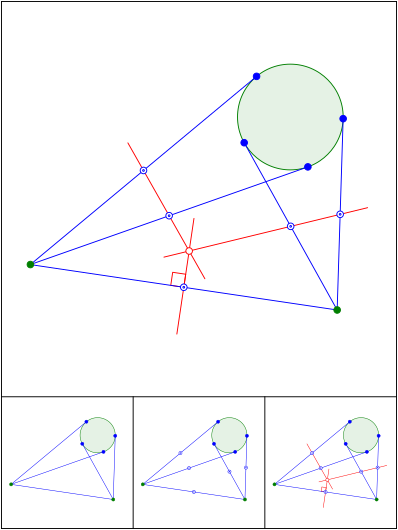
Schnittpunkt 567
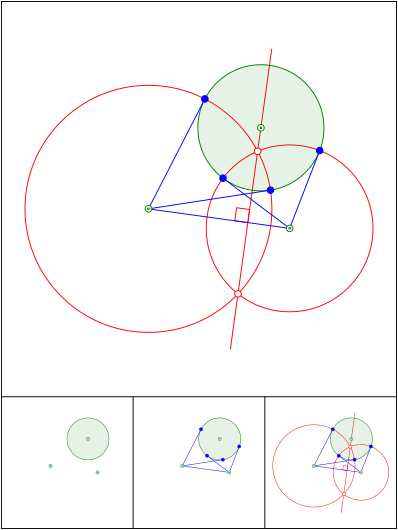
Schnittpunkt 568
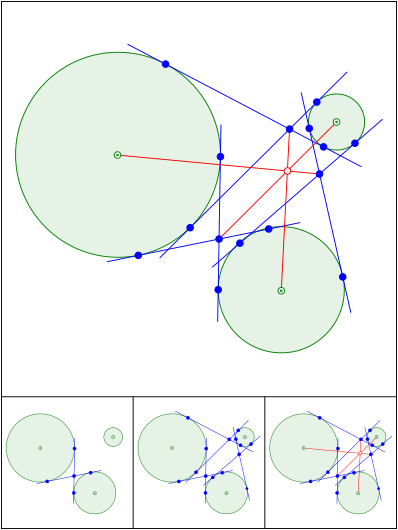
Schnittpunkt 569

Thaleskreise ber harmonischen Punktepaaren
Schnittpunkt 570

Thaleskreise ber harmonischen Punktepaaren
Schnittpunkt 571
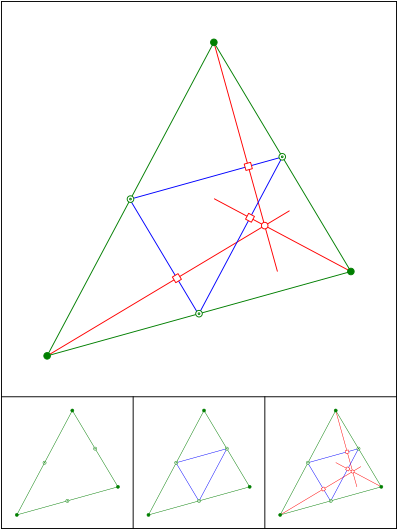
Henu so de
Schnittpunkt 572
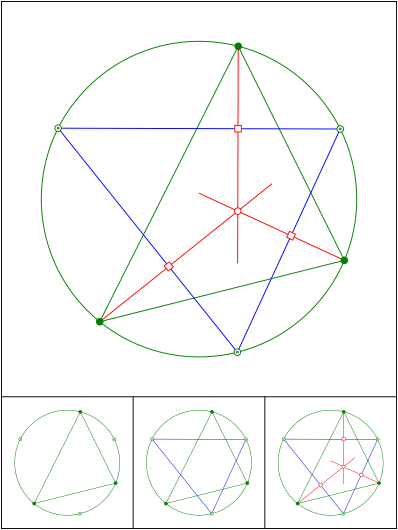
Schnittpunkt 573
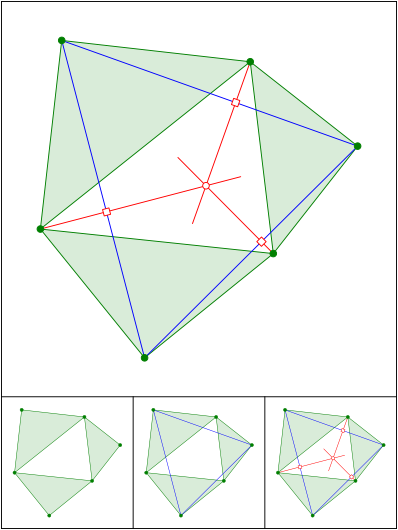
Schnittpunkt 574
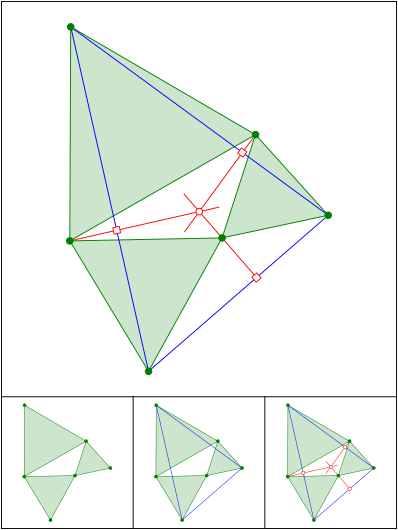
Schnittpunkt 575
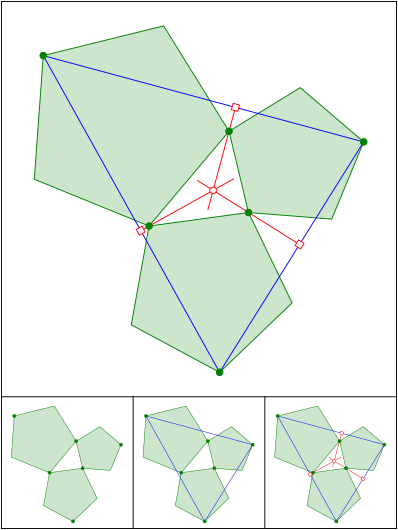
Schnittpunkt 576
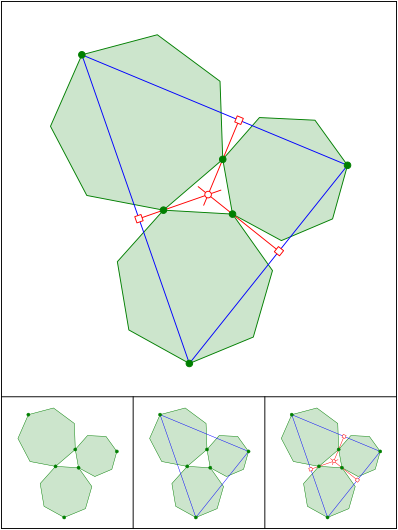
Schnittpunkt 577
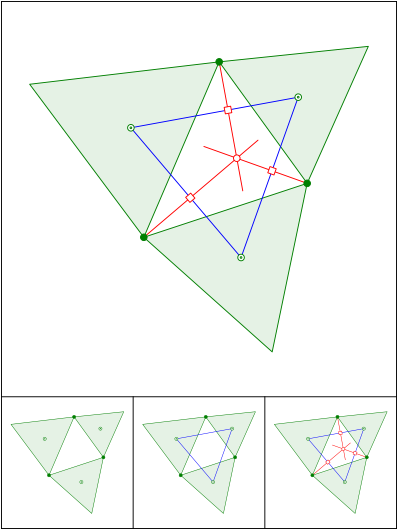
Schnittpunkt 578
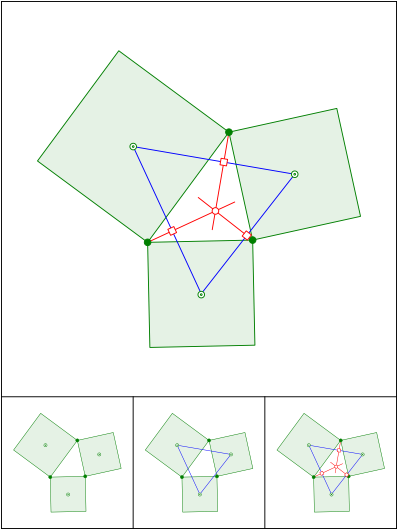
Schnittpunkt 579
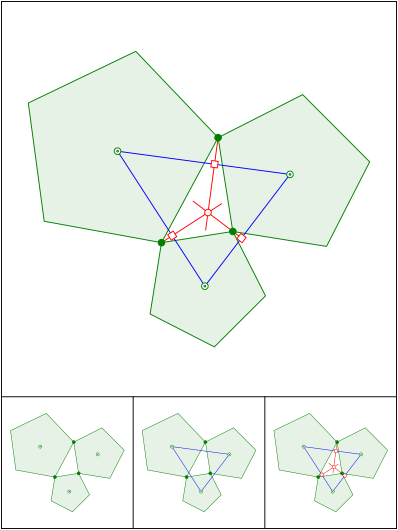
Schnittpunkt 580
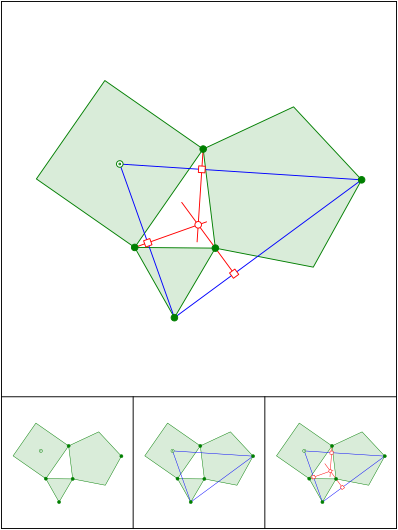
Schnittpunkt 581
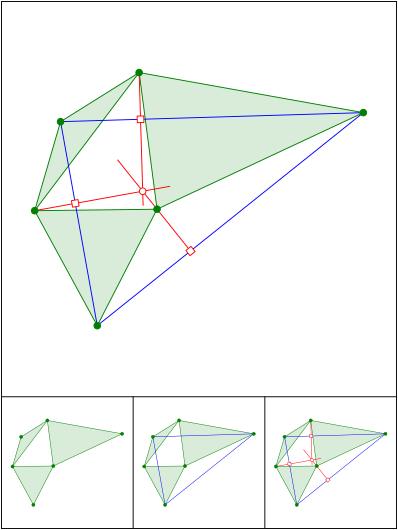
Beliebige gleichschenklige Dreiecke
Schnittpunkt 582
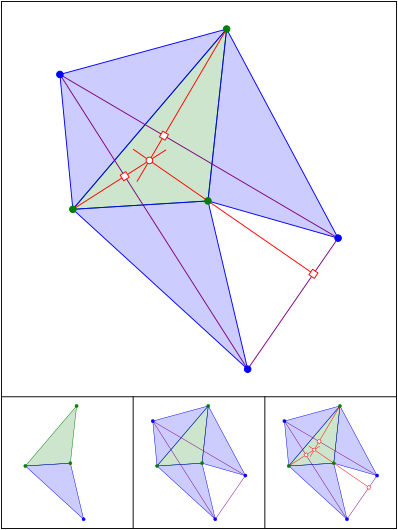
Schnittpunkt 583
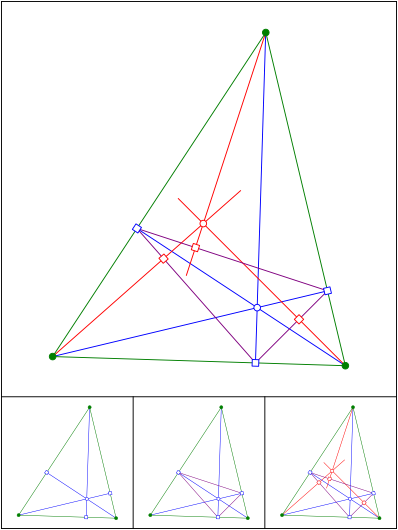
Hhenfu§punkte
Schnittpunkt 584
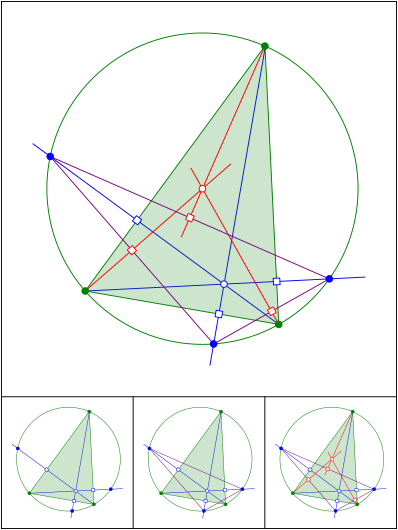
Schnittpunkt 585
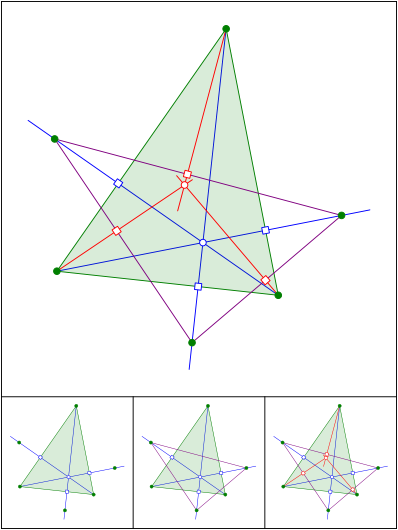
Beliebige Punkte auf den Hhen
Schnittpunkt 586
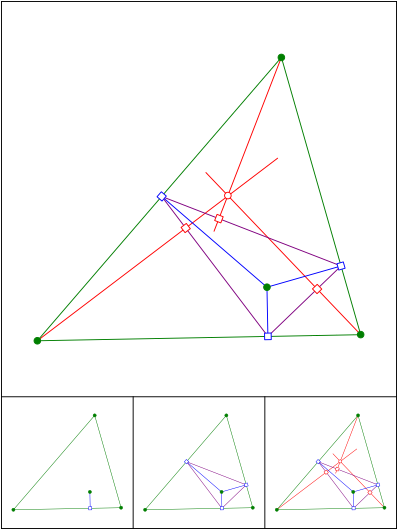
Schnittpunkt 587
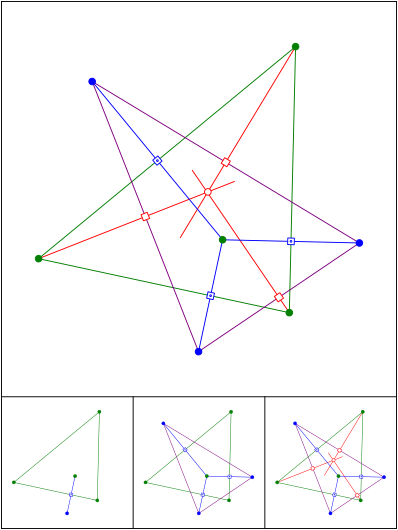
Herausspiegeln
Schnittpunkt 588
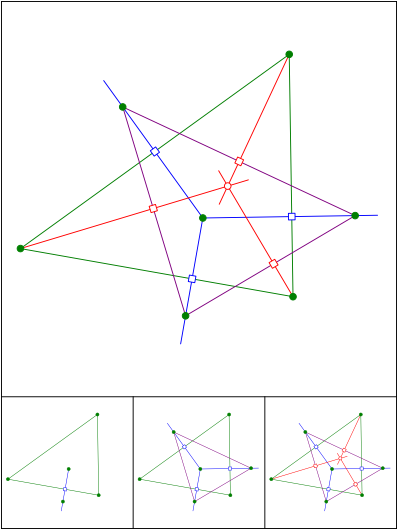
Schnittpunkt 589
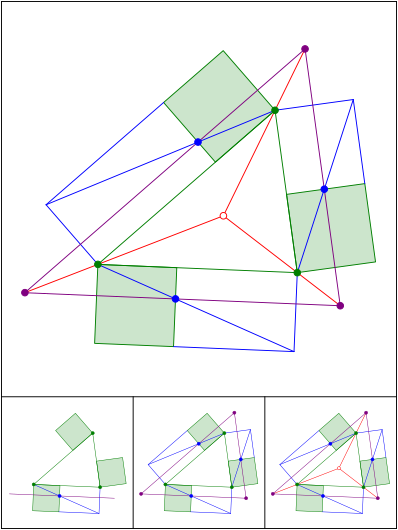
Auch so gehtÕs.
Schnittpunkt 590
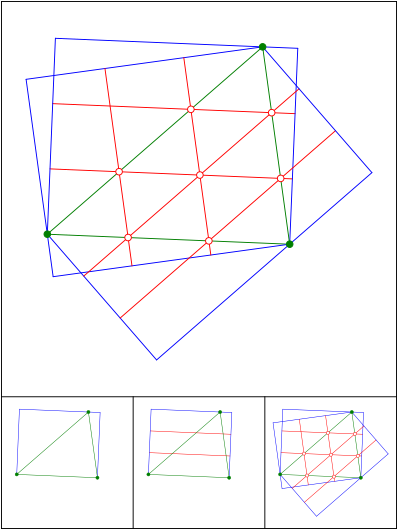
Schnittpunkt 591
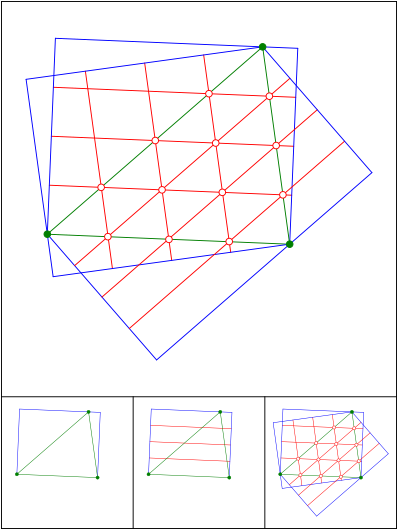
Schnittpunkt 592
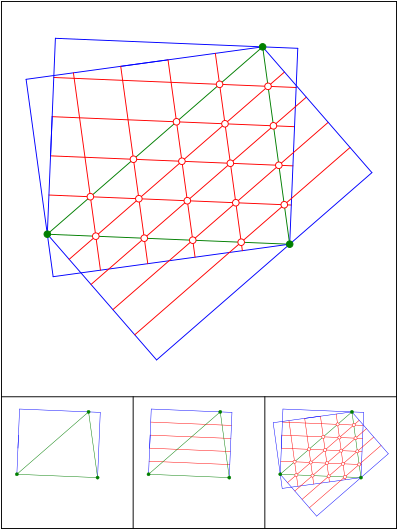
Schnittpunkt 593
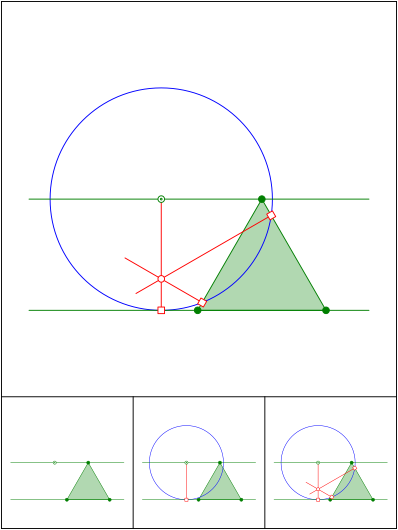
Reuleaux
Schnittpunkt 594
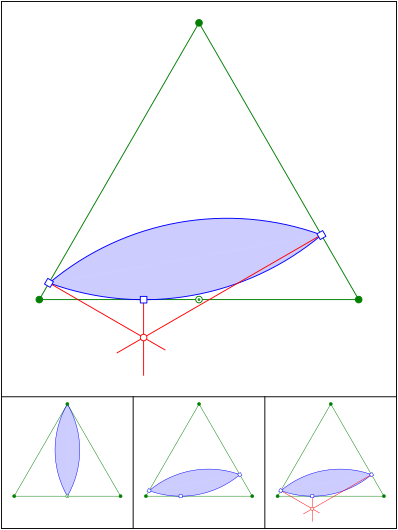
Reuleaux
Schnittpunkt 595
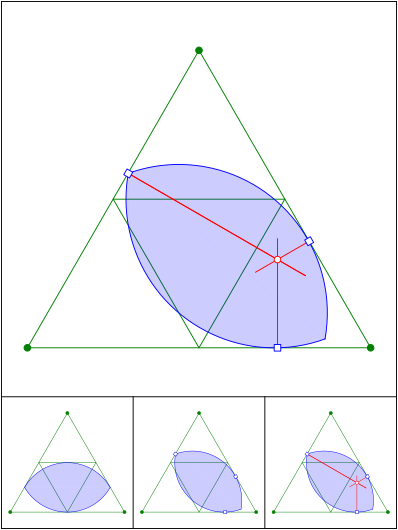
Reuleaux
Schnittpunkt 596
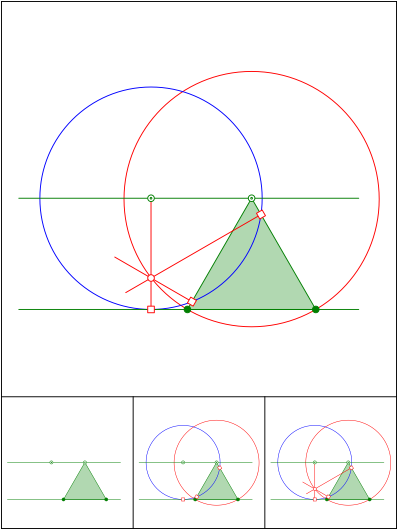
Reuleaux
Schnittpunkt 597
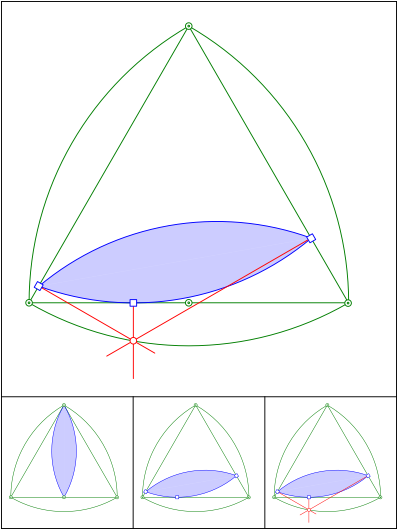
Reuleaux
Schnittpunkt 598
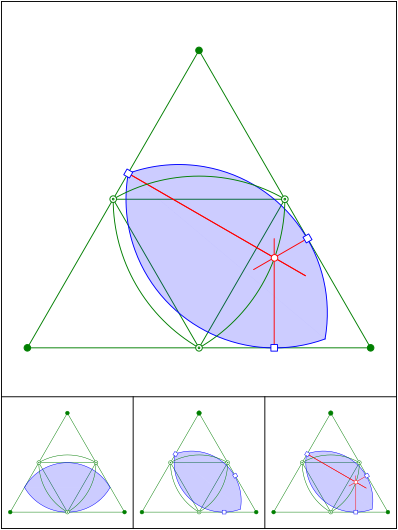
Reuleaux
Schnittpunkt 599
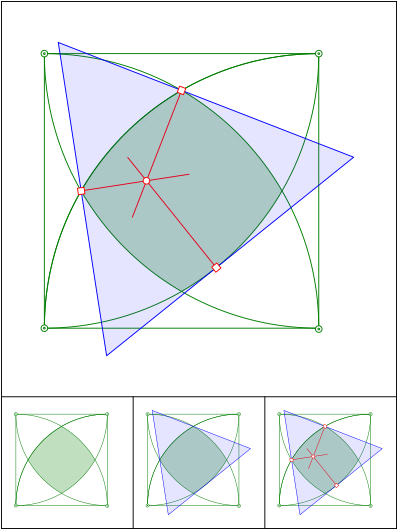
Schnittpunkt 600
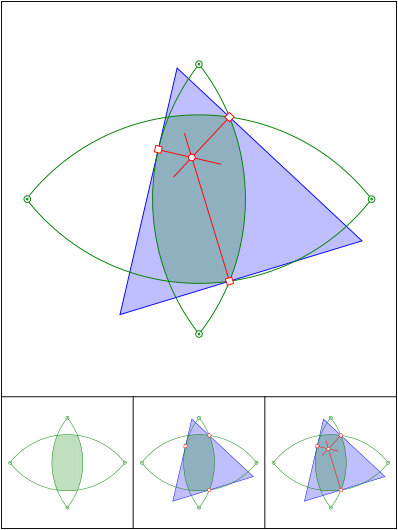
Literatur
Baptist, Peter (1992): Die Entwicklung der neueren Dreiecksgeometrie. Mannheim: B.I.Wissenschaftsverlag. ISBN 3-411-15661-9
Donath, Emil (1976): Die merkwrdigen Punkte und Linien des ebenen Dreiecks. Berlin: Deutscher Verlag der Wissenschaften, 3. Auflage 1976.
Eddy, R.H.
/ Fritsch, R. (1994): The Conics of Ludwig Kiepert: A Comprehensive Lesson in
the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June 1994,
p. 188-205
Euklid (1980): Die Elemente. Nach Heibergs Text aus dem Griechischen bersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft. ISBN 3-534-01488-X
G.-M., F.
(1920/1991): Exercices de Gomtrie. Sixime dition. Tours - Paris: Mame - de
Gigord 1920. Rimpression de la 6e dition publie par Mame et De Gigord en 1920.
Sceaux: Gabay 1991. ISBN 2-87647-083-7
Gtzl, Dieter (2006): Besondere Linien im Dreieck – eine Verallgemeinerung. MNU Der mathematische und naturwissenschaftliche Unterricht. 59/8, S. 468-471, ISSN 0025-5866
Haag, Wilfried (2003): Wege zu geometrischen Stzen. Stuttgart: Klett. ISBN 3-12-720120-6
Hauptmann, W. (1995): Erzeugung ãmerkwrdiger PunkteÒ. PM Praxis der Mathematik 37, S. 8
Hoehn, Larry (2001): Extriangles and Excevians. Mathematics Magazine, Vol. 74, No. 5, p. 384-388
Jacobi, C. F. A. (1825): De triangulorum rectilineorum proprietatibus quibusdam nondum satis cognitis. Naumburg.
Kimberling, Clark (1998): Triangle Centers and Central Triangles. Congr. Numer. 129, p. 1 – 295
Klemenz, Heinz (2003): Merkwrdiges im Dreieck. VSMP Bulletin, herausgegeben vom Verein Schweizerischer Mathematik- und Physiklehrer, No 91, S. 16-23
Walser, Hans (1990-1994): Schlusspunkt. Didaktik der Mathematik, 18 (1990) bis 22 (1994), jeweils letzte Heftseite
Walser, Hans (1993): Die Eulersche Gerade als Ort "merkwrdiger Punkte". Didaktik der Mathematik (21), 95-98
Walser, Hans (1994): Eine Verallgemeinerung der Winkelhalbierenden. Didaktik der Mathematik (22), S. 50-56
Walser, Hans (2000): Lattice Geometry and Pythagorean Triangles. ZDM Zentralblatt fr Didaktik der Mathematik. Jahrgang 32, Heft 2, S. 32 - 35
Walser, Hans (2003): Eine Schar von Schnittpunkten im Dreieck. Praxis der Mathematik (2/45), S. 66 - 68
Walser, Hans (2006): 99 Points of Intersection. Examples – Pictures – Proofs. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America. ISBN 0-88385-553-4
Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1
Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.
Wildberger, Norman J. (2010): Chromogeometry. The Mathematical Intelligencer. Volume 32, Number 1. Springer. p. 26-32