Hans Walser
Schnittpunkte 601 - 700
Die Bildsequenzen sind als Bilder ohne Worte konzipiert.
Farbreihenfolge: Dunkelgrn, blau, rot. Nach Bedarf werden auch andere Farben verwendet.
Die drei kleinen Bilder im Querstreifen deuten die Entstehung der Gesamtfigur an.
Gegebenenfalls finden sich unterhalb der Figur Literaturangaben oder Hinweise auf Anregungen, die zu diesen Figuren gefhrt haben.
Letzte nderung 7. Mrz 2017
Schnittpunkt 601
Schnittpunkt 602
Schnittpunkt 603
Schnittpunkt 604
Schnittpunkt 605
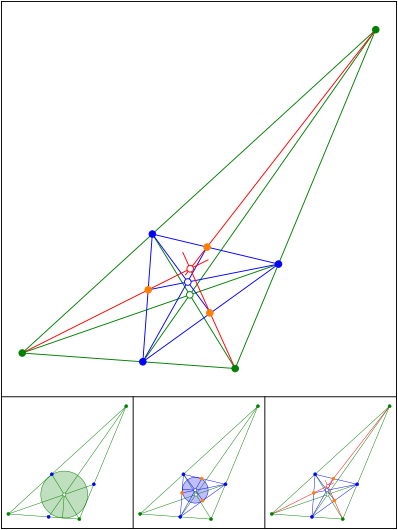
Schnittpunkt 606
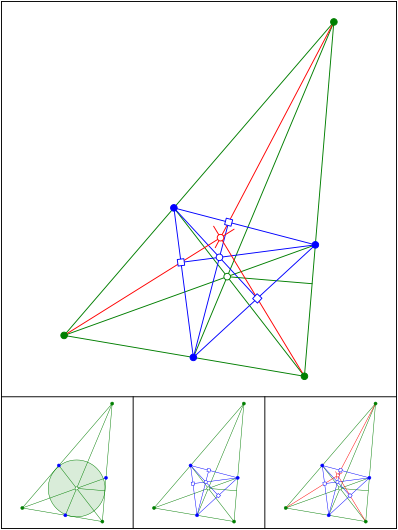
Schnittpunkt 607
Zweimal Ceva
Schnittpunkt 608
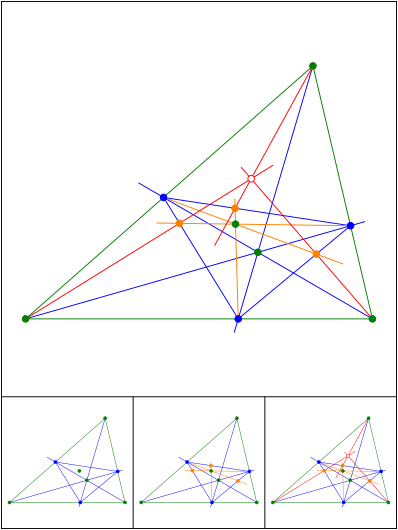
Menelaus, harmonische Punkte, Ceva
Schnittpunkt 609
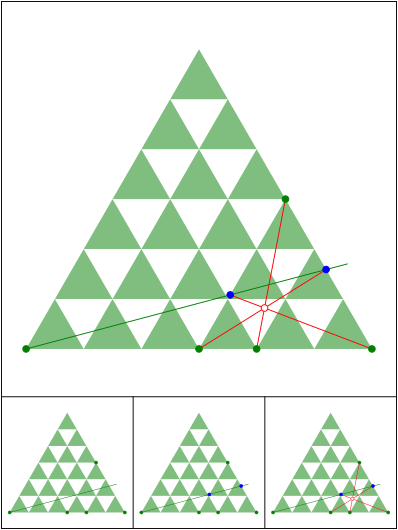
Schnittpunkt 610
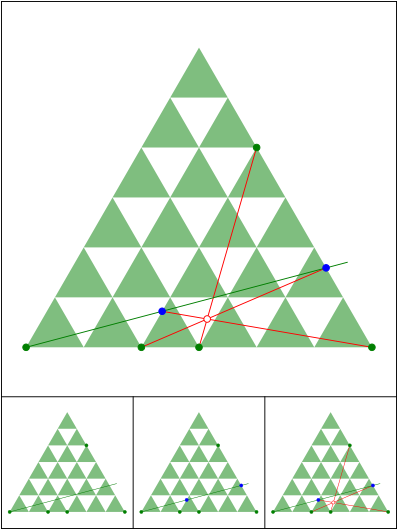
Schnittpunkt 611
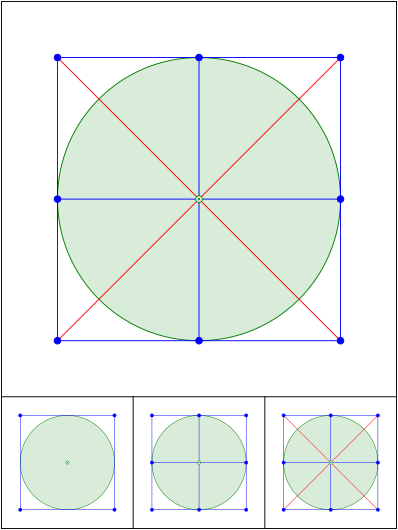
Na ja
Schnittpunkt 612
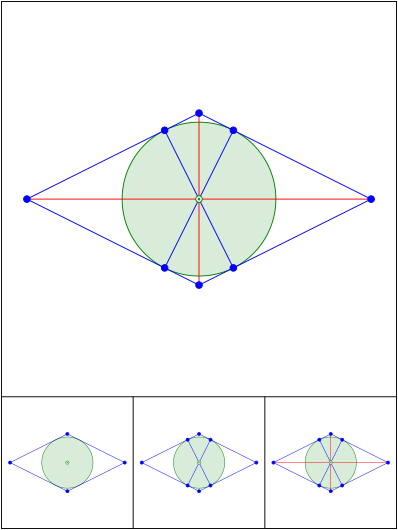
Rhombus
Schnittpunkt 613
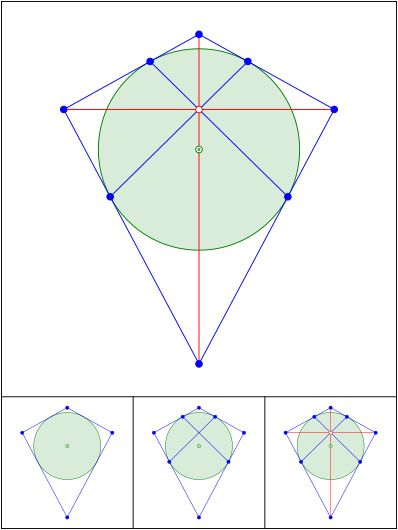
Drachen
Schnittpunkt 614
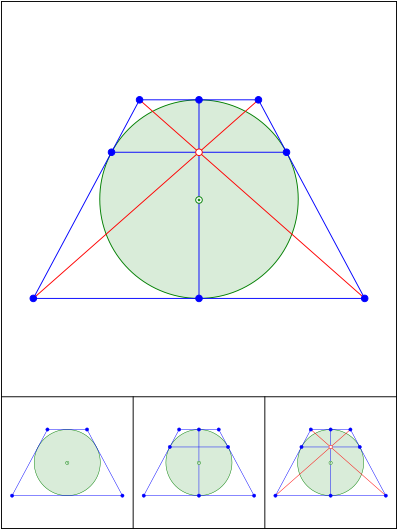
Schnittpunkt 615
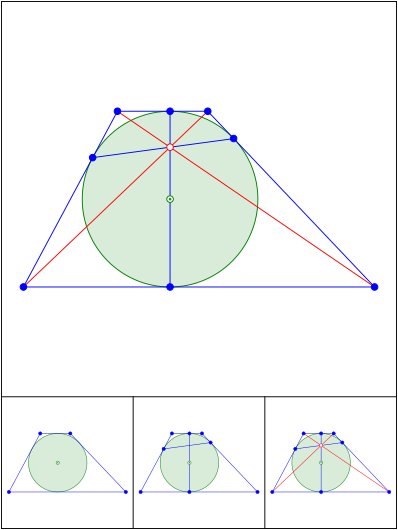
Schnittpunkt 616
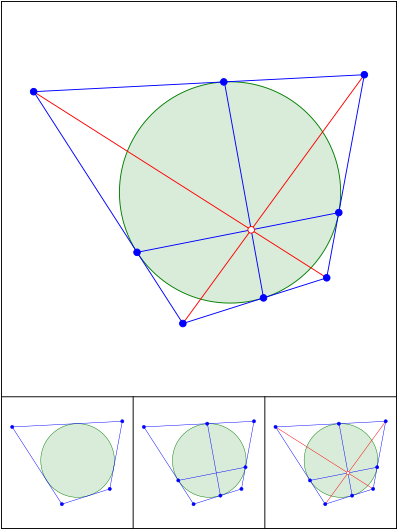
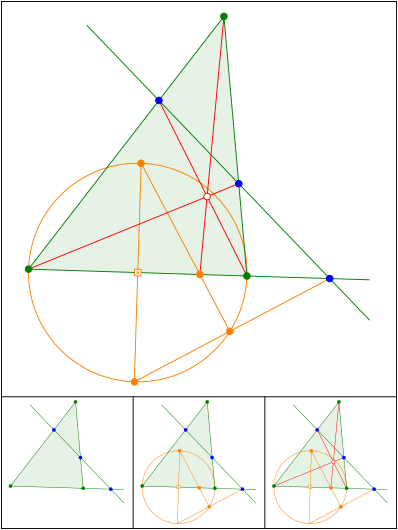
Tangentenviereck.
Newton. (vgl. G.-M., F. 1920/1991,
S. 573)
Schnittpunkt 617
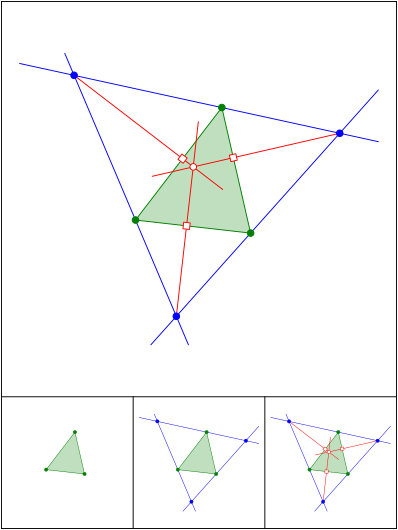
u§ere Winkelhalbierende
Schnittpunkt 618
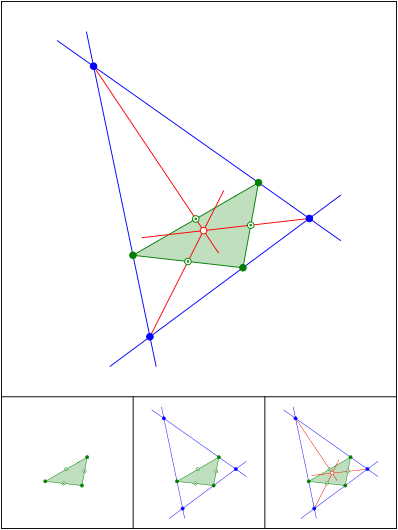
u§ere Winkelhalbierende
Schnittpunkt 619
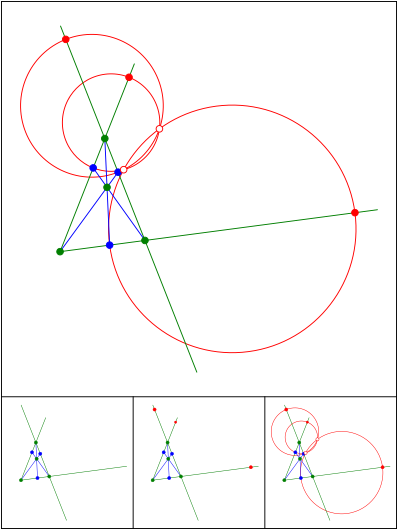
Kreise des Apollonius
Schnittpunkt 620
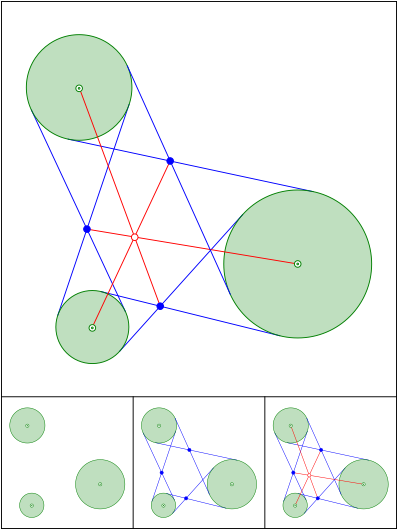
Vermutlich ein alter Bekannter
Schnittpunkt 621
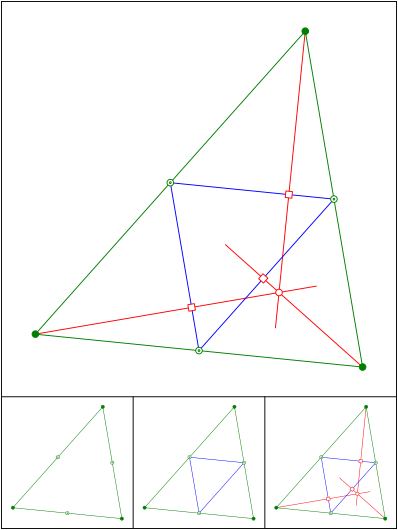
Hhenschnittpunkt neu erfunden
Schnittpunkt 622
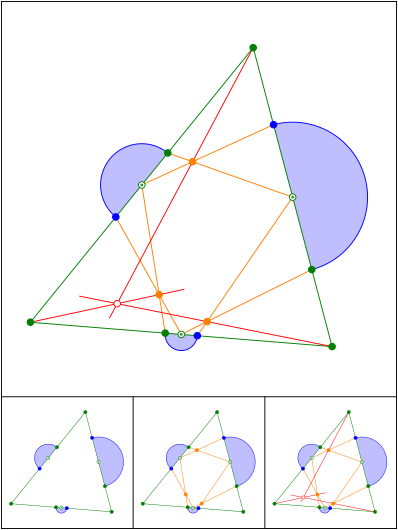
Schnittpunkt 623
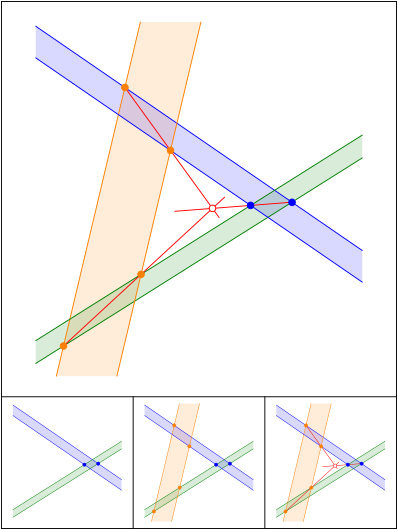
Schnittpunkt 624
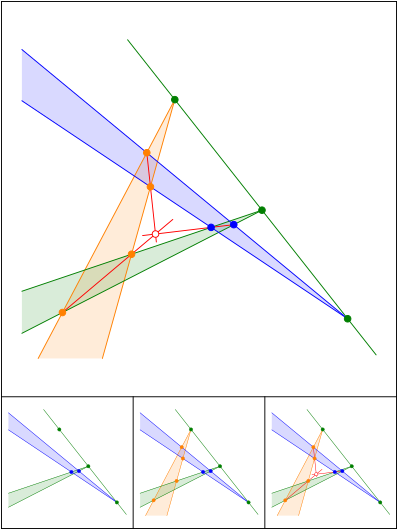
Schnittpunkt 625
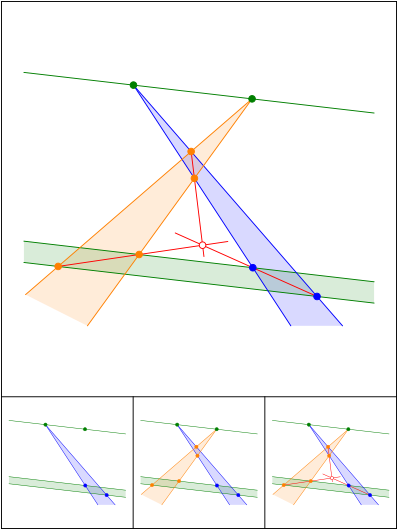
Schnittpunkt 626
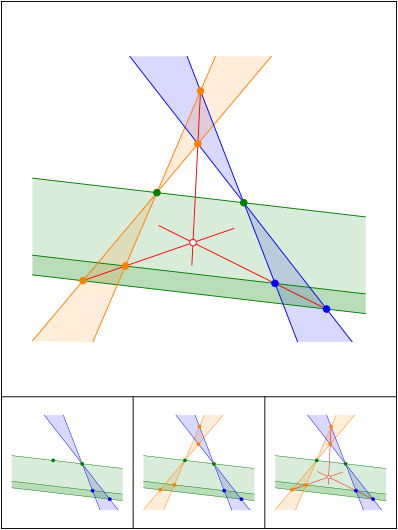
Schnittpunkt 627
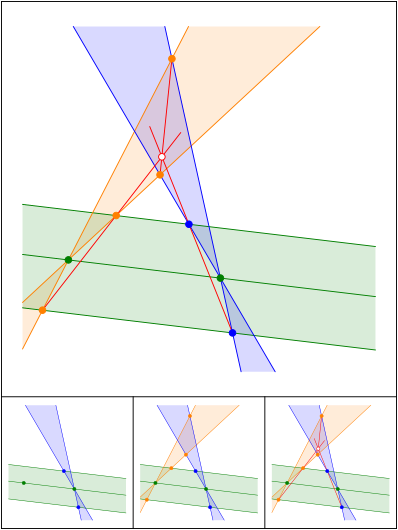
Schnittpunkt 628
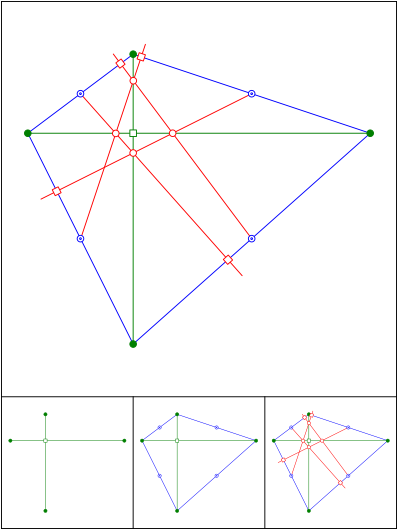
Schnittpunkt 629
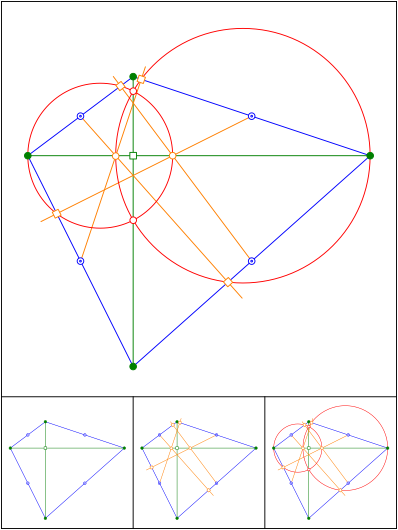
Schnittpunkt 630
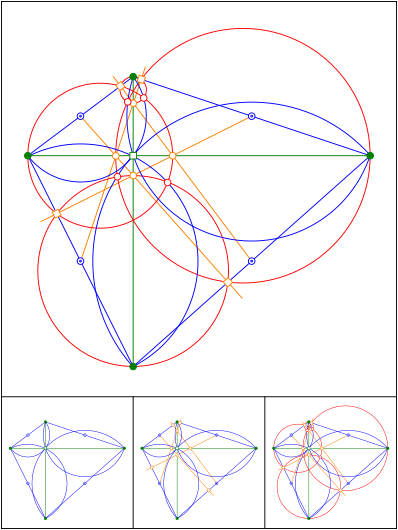
Schnittpunkt 631
Der Strahlensatz ist immer wieder lustig.
Schnittpunkt 632
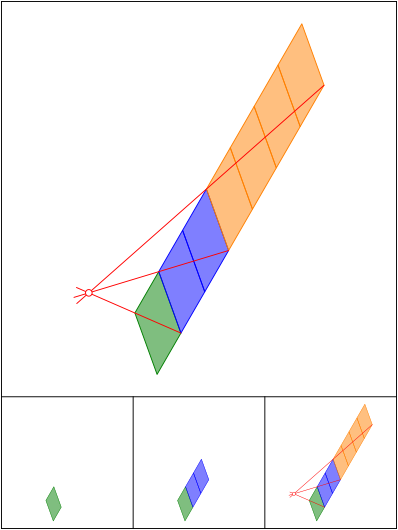
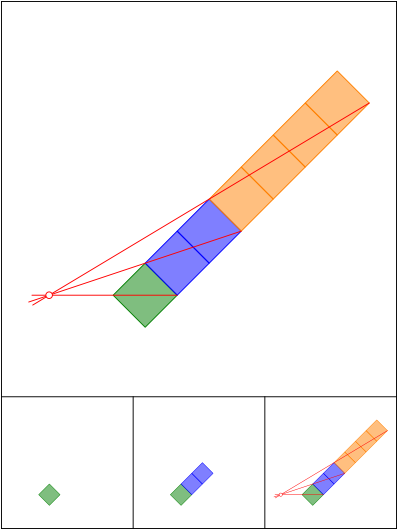
Schnittpunkt 633
Schnittpunkt 634
Schnittpunkt 635
Normalaxonometrisches Wrfelbild (Orthografische Projektion)
Schnittpunkt 636
Schnittpunkt 637
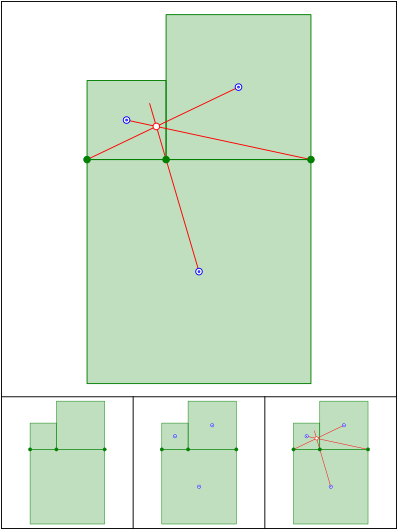
Gru§ von Kiepert
Schnittpunkt 638
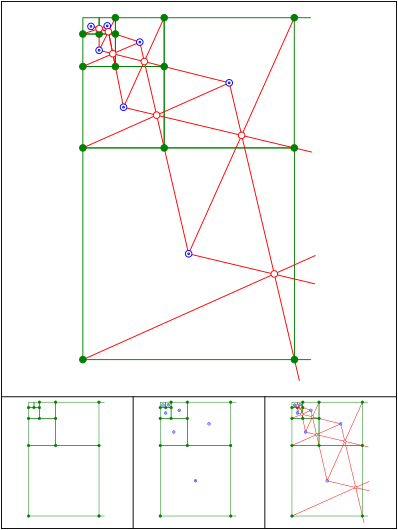
Fibonacci-Quadrate. Die roten Linien sind nicht parallel.
Schnittpunkt 639
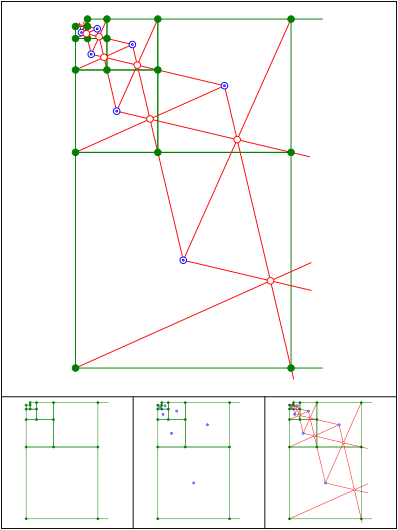
Goldener Schnitt. Die roten Linien sind parallel.
Schnittpunkt 640
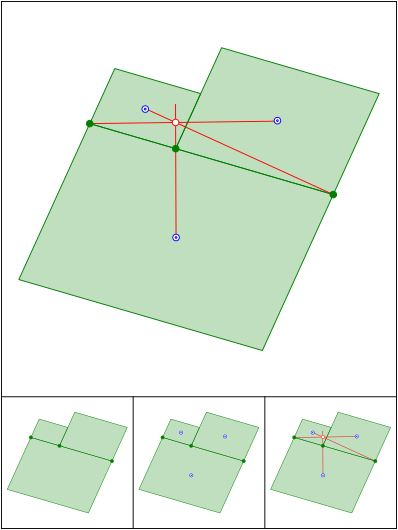
Schnittpunkt 641
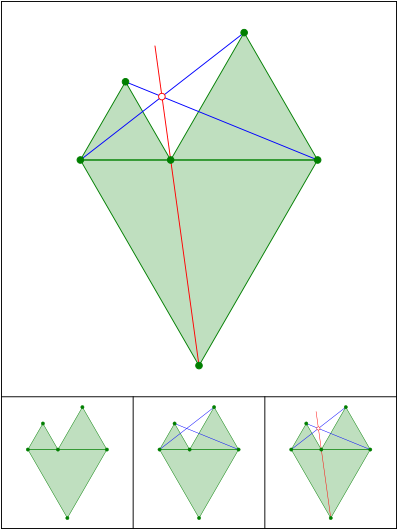
Gru§ von Fermat
Schnittpunkt 642
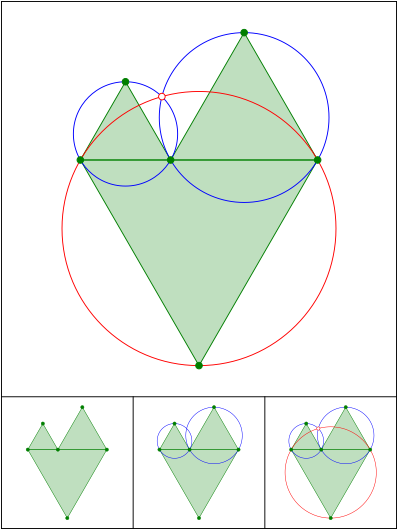
Noch ein Gru§ von Fermat
Schnittpunkt 643
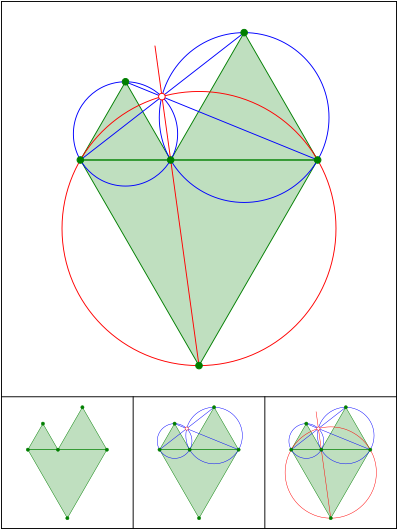
Schnittpunkt 644
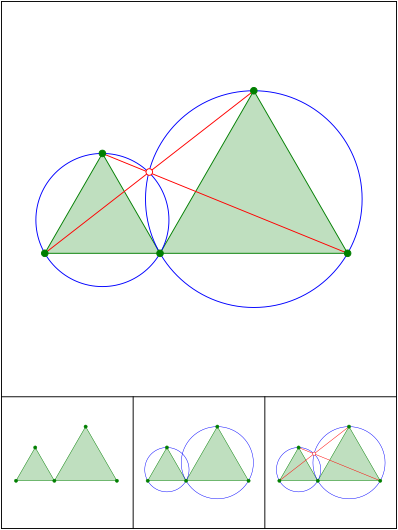
Schnittpunkt 645
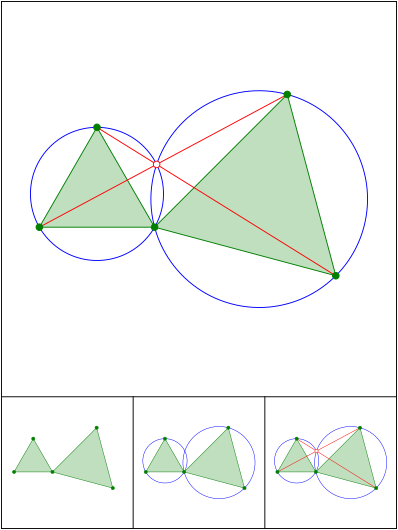
Ein alter Bekannter
Schnittpunkt 646
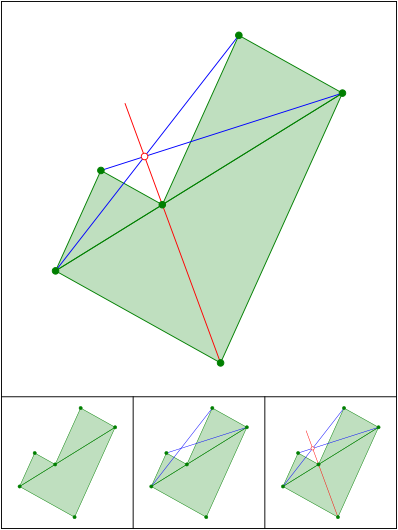
Schnittpunkt 647
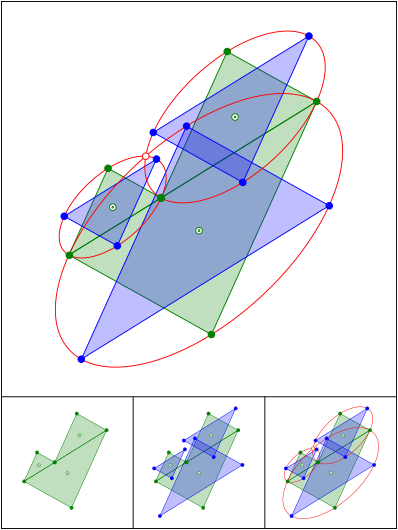
Steiner-Umellipsen
Schnittpunkt 648
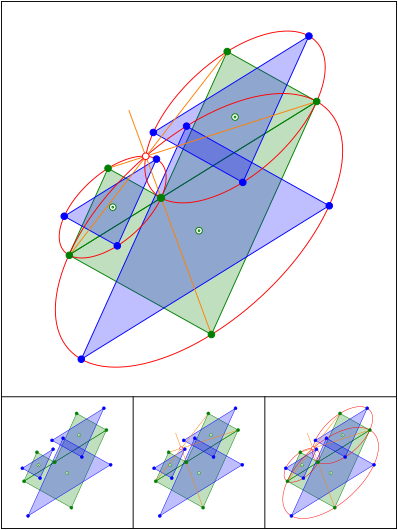
Schnittpunkt 649
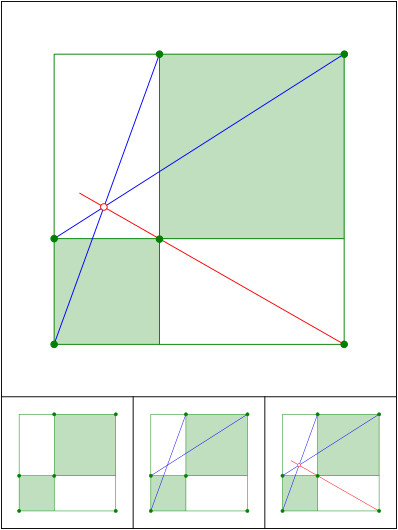
Schnittpunkt 650
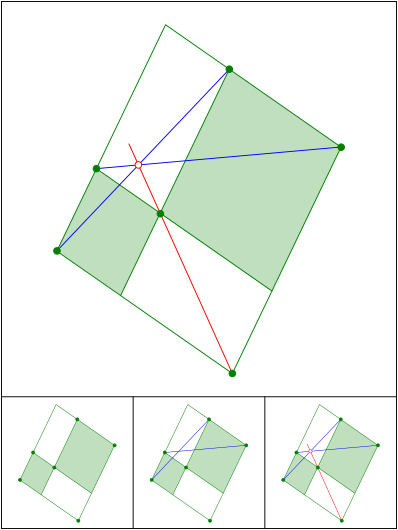
Schnittpunkt 651
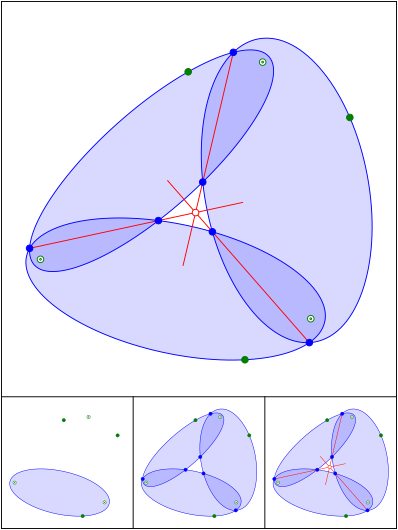
Konfokale Ellipsen
Schnittpunkt 652
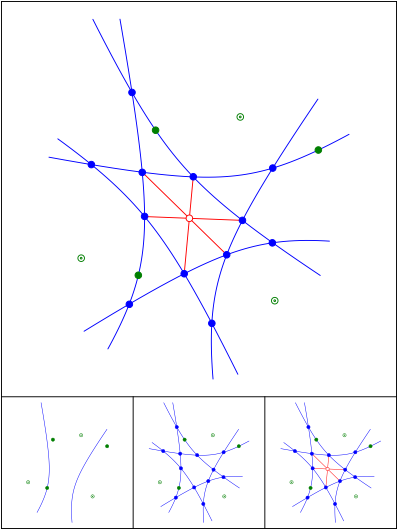
Konfokale Hyperbeln
Schnittpunkt 653
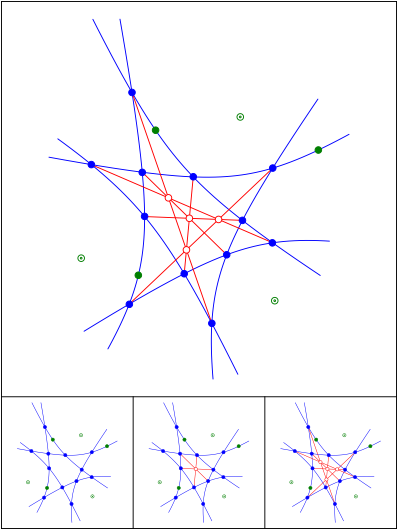
Konfokale Hyperbeln
Schnittpunkt 654

Konfokale Kegelschnitte
Schnittpunkt 655
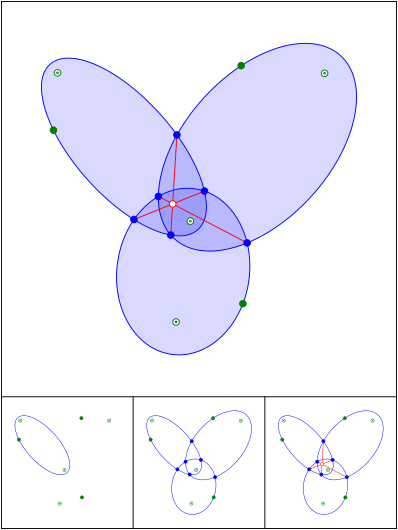
Konfokale Ellipsen
Schnittpunkt 656
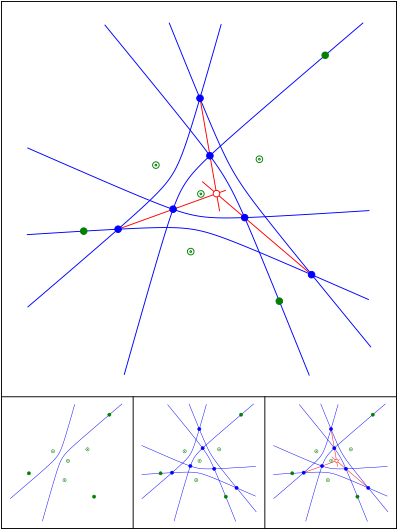
Konfokale Hyperbeln
Schnittpunkt 657
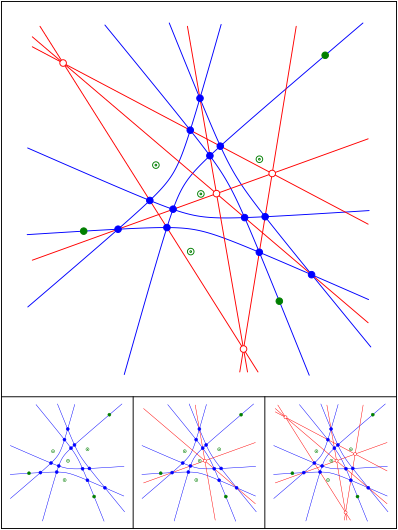
Konfokale Hyperbeln
Schnittpunkt 658
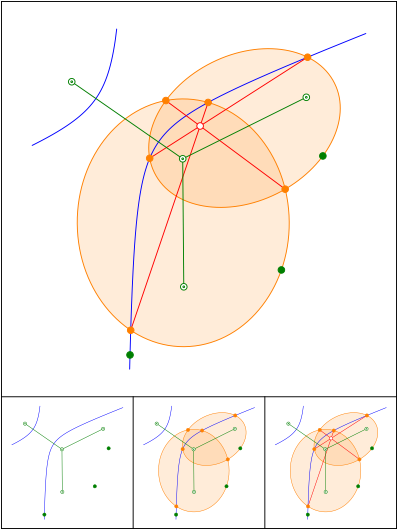
Schnittpunkt 659
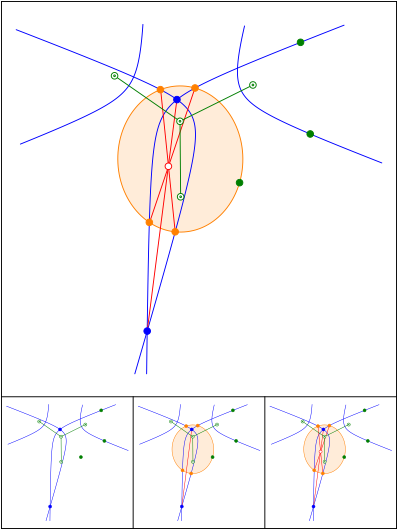
Schnittpunkt 660
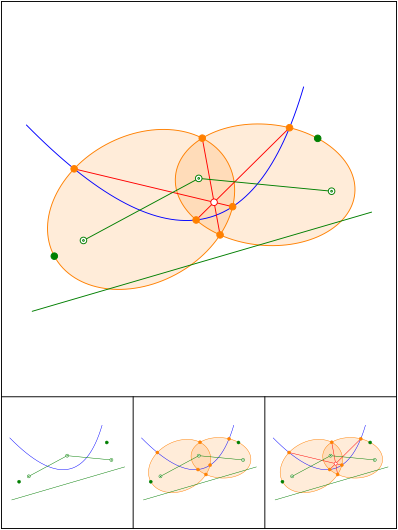
Konfokale Parabel und Ellipsen
Schnittpunkt 661
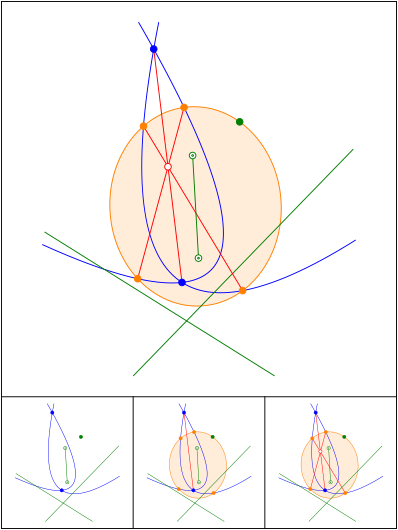
Konfokale Parabeln und Ellipse
Schnittpunkt 662
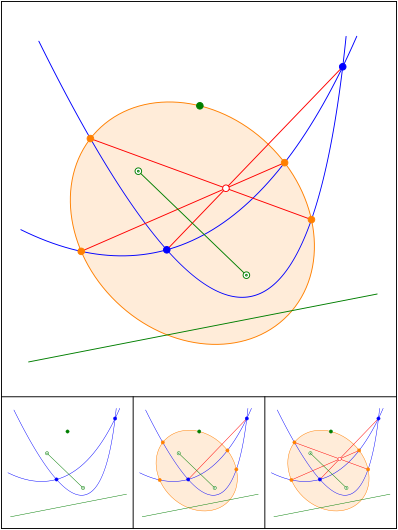
Schnittpunkt 663
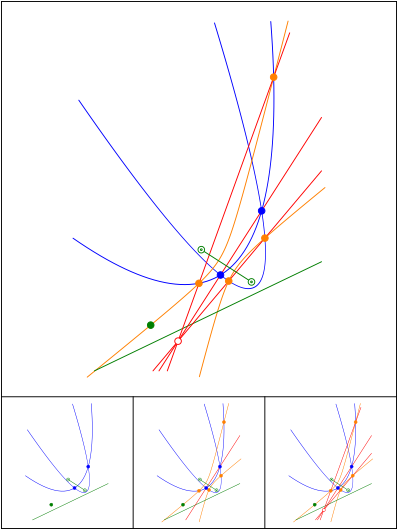
Schnittpunkt 664
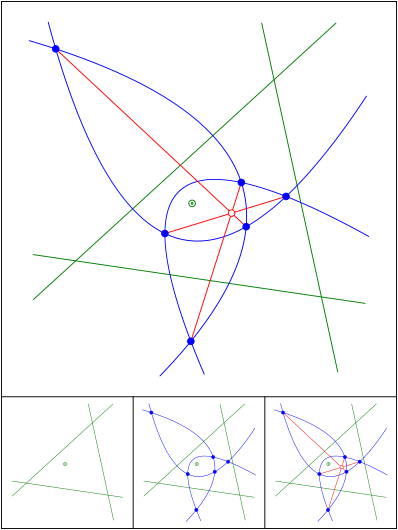
Drei konfokale Parabeln
Schnittpunkt 665
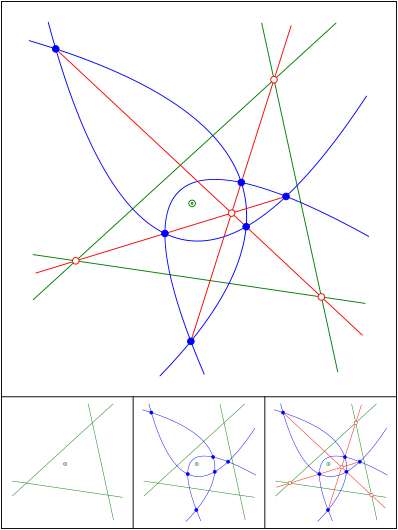
Ein alter Bekannter
Schnittpunkt 666
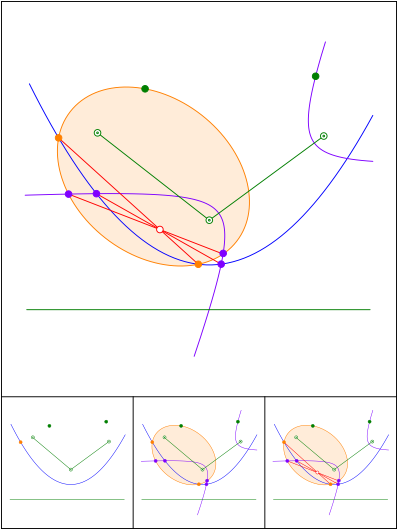
Parabel, Ellipse, Hyperbel
Schnittpunkt 667
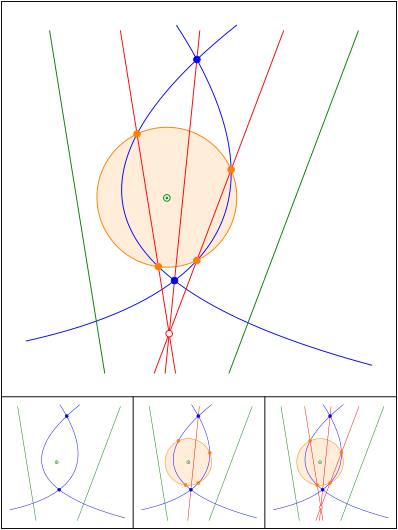
Schnittpunkt 668
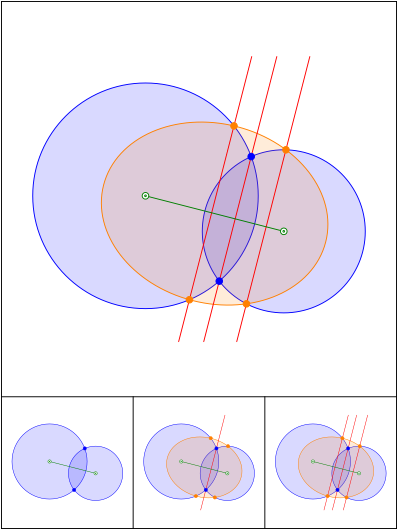
Schnittpunkt im Unendlichen
Schnittpunkt 669
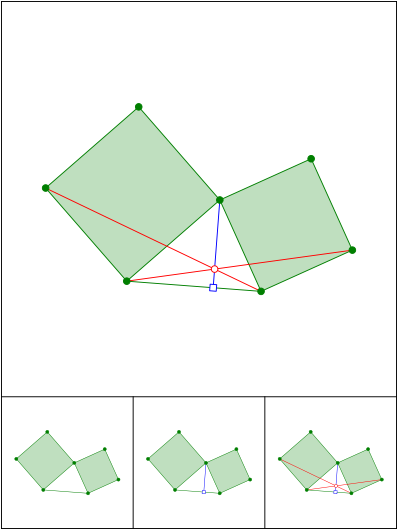
Kein rechtwinkliges Dreieck
Schnittpunkt 670
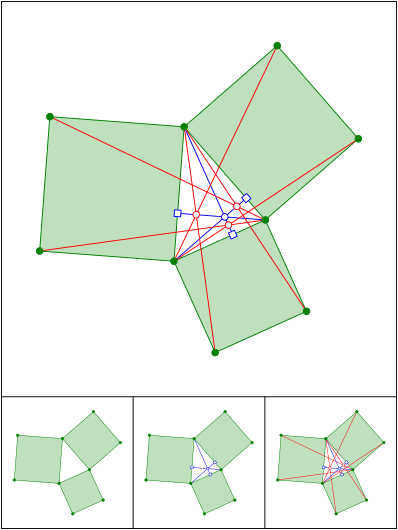
Schnittpunkt 671
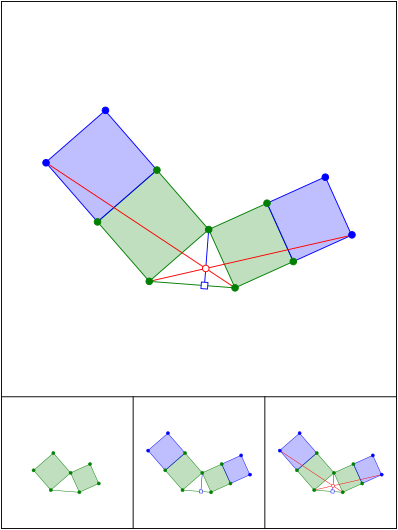
Schnittpunkt 672
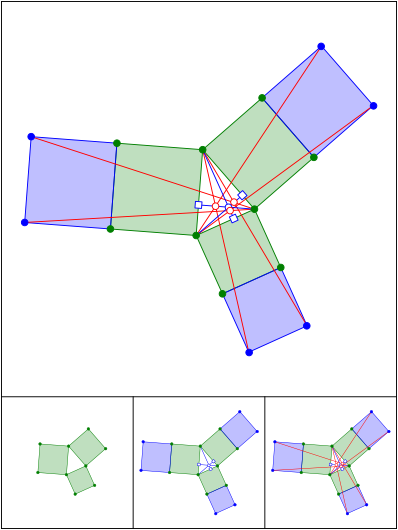
Schnittpunkt 673
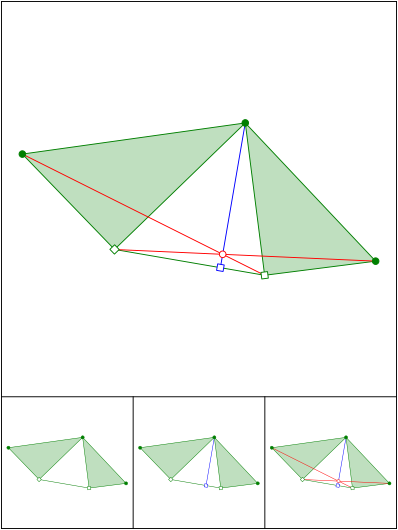
hnliche rechtwinklige Dreiecke
Schnittpunkt 674
Manfred Schmelzer, Regensburg
Schnittpunkt 675
Feuerbach
Schnittpunkt 676
Schnittpunkt 677

Streifen auf Keil
Schnittpunkt 678
Keil auf Keil
Schnittpunkt 679
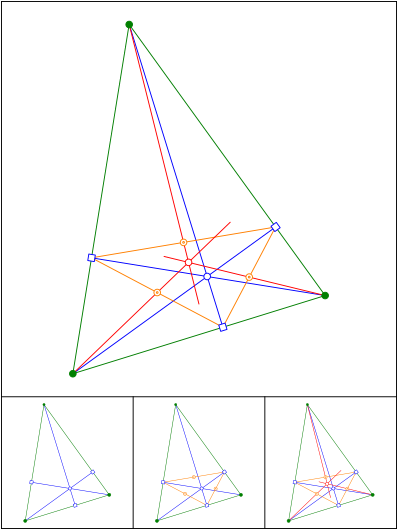
Hhenfu§punktdreieck
Schnittpunkt 680
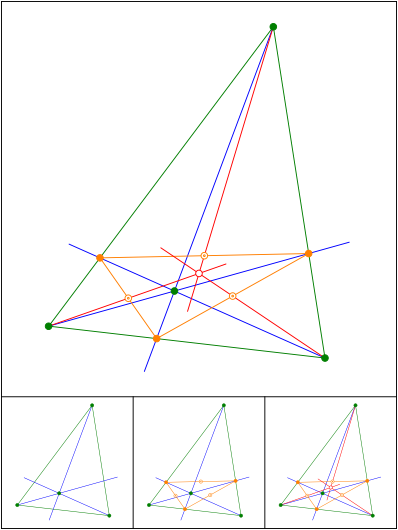
Ceva-Fu§punktdreieck
Schnittpunkt 681
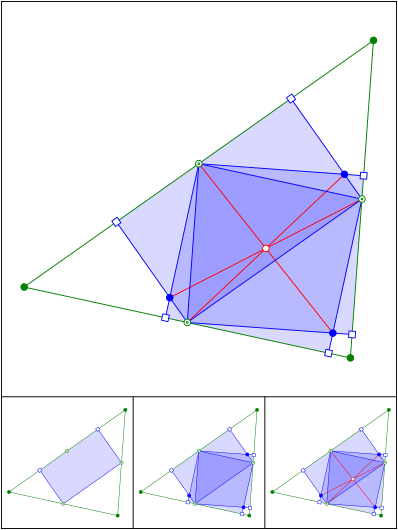
Optimale Rechtecke einpassen
Schnittpunkt 682
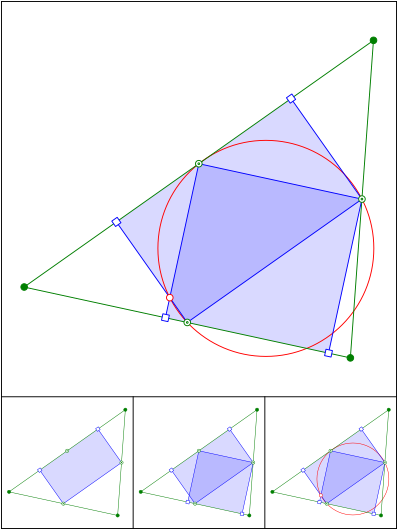
Optimale Rechtecke und Feuerbachkreis
Schnittpunkt 683
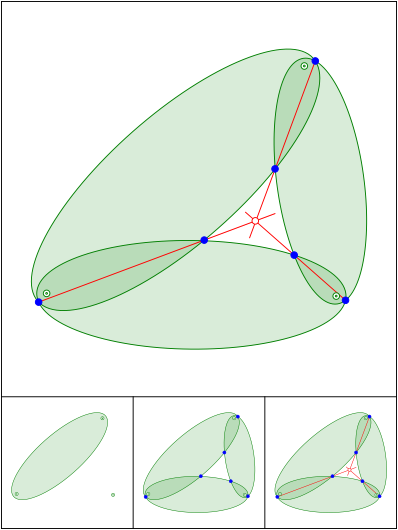
hnliche Ellipsen mit gemeinsamen Brennpunkten. Vgl. 651
Schnittpunkt 684
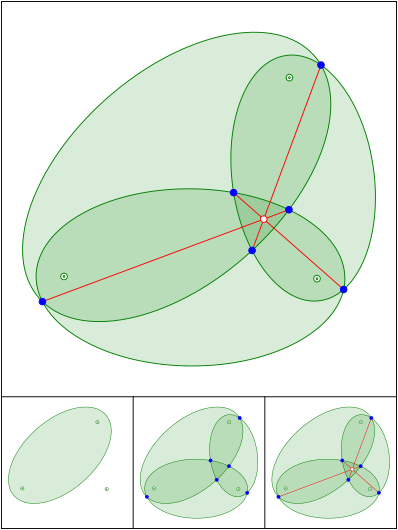
hnliche Ellipsen mit gemeinsamen Brennpunkten
Schnittpunkt 685
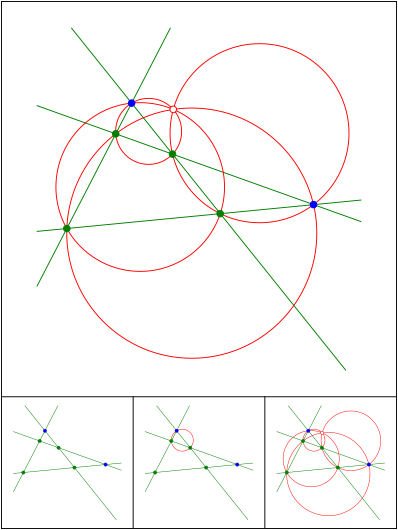
Schnittpunkt 686
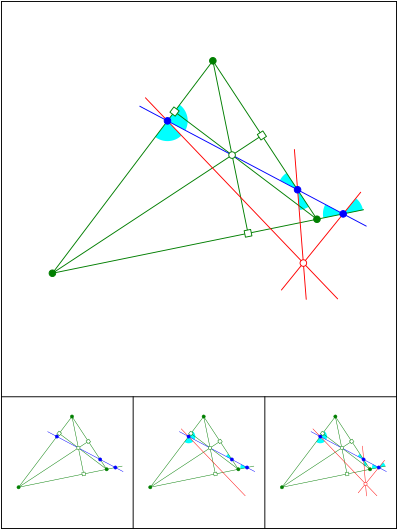
Schnittpunkt 687
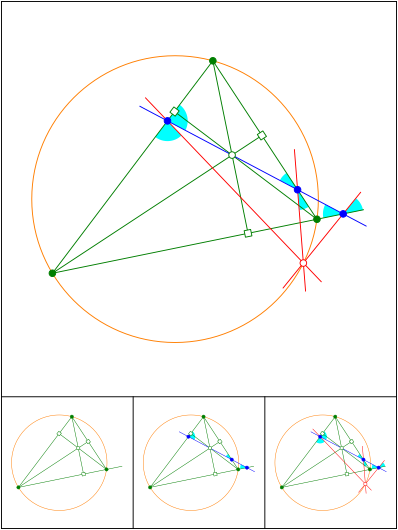
Schnittpunkt 688
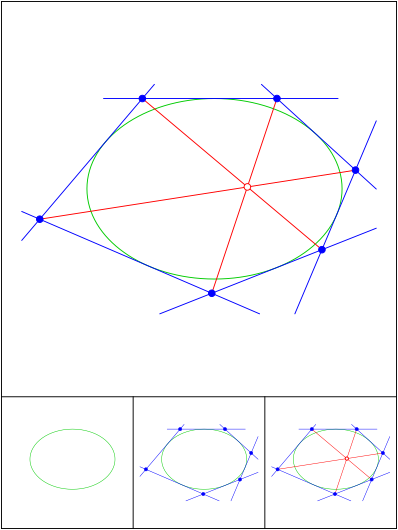
Brianchon
Schnittpunkt 689
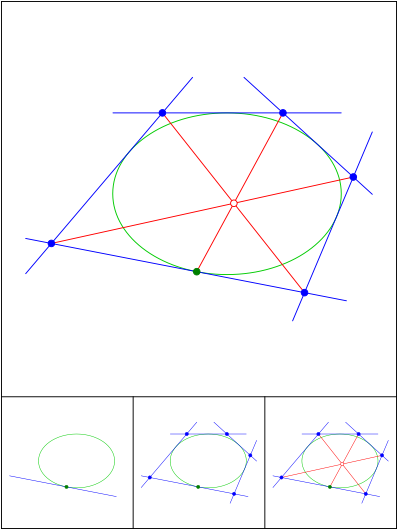
Brianchon
Schnittpunkt 690
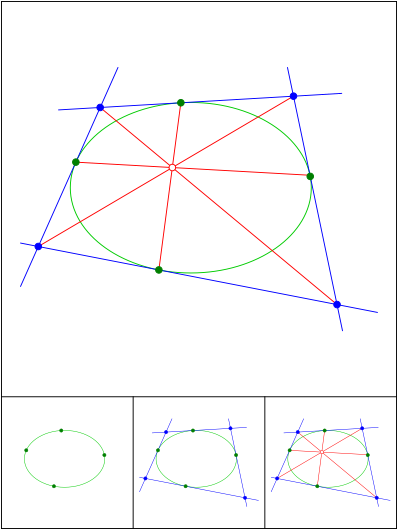
Newton, Brianchon
Schnittpunkt 691
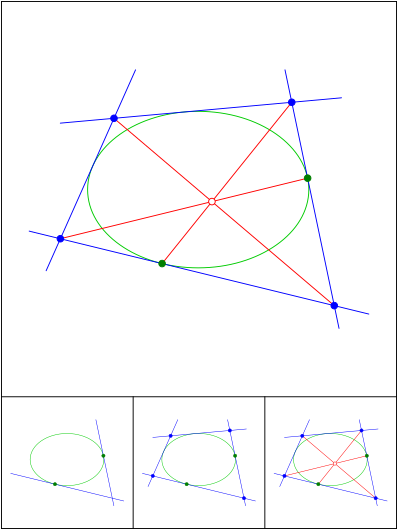
Brianchon
Schnittpunkt 692
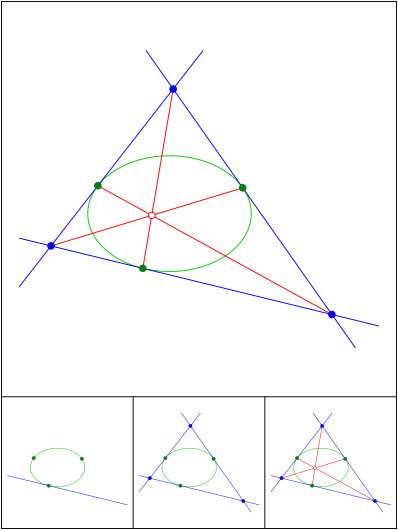
Brianchon
Schnittpunkt 693
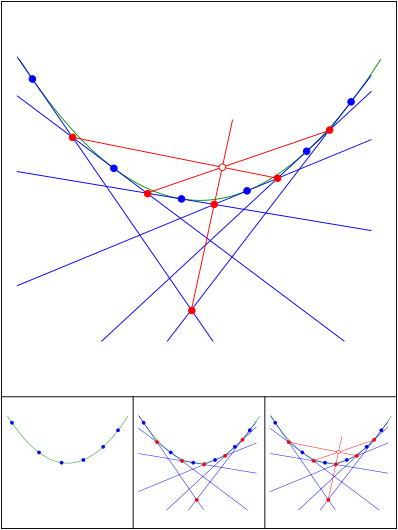
Brianchon
Schnittpunkt 694

Brianchon
Schnittpunkt 695

Brianchon zum fnften
Schnittpunkt 696

Brianchon zum vierten
Schnittpunkt 697
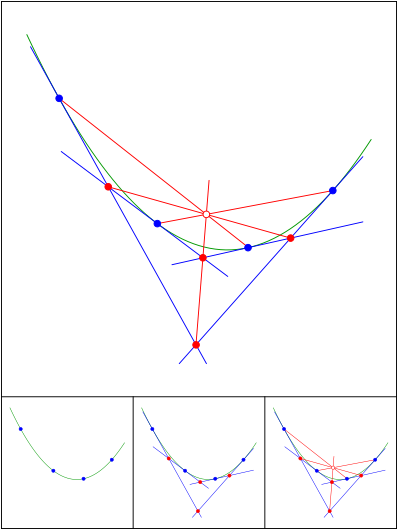
Newton und Brianchon
Schnittpunkt 698
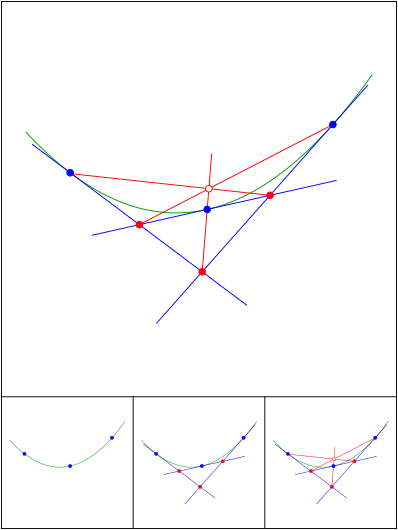
Brianchon zum dritten
Schnittpunkt 699
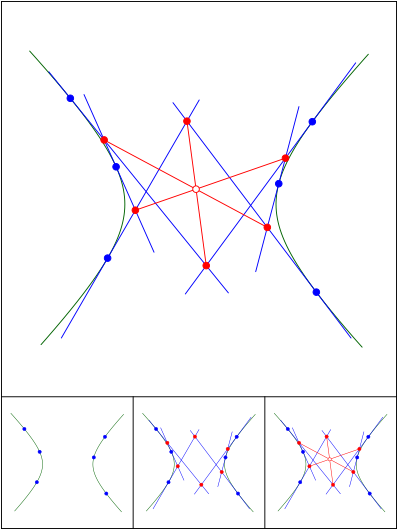
Brianchon zum sechsten
Schnittpunkt 700
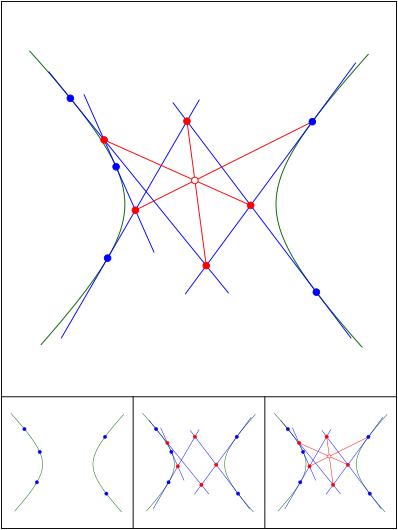
Brianchon zum fnften
Literatur
Baptist, Peter (1992): Die Entwicklung der neueren Dreiecksgeometrie. Mannheim: B.I.Wissenschaftsverlag. ISBN 3-411-15661-9
Donath, Emil (1976): Die merkwrdigen Punkte und Linien des ebenen Dreiecks. Berlin: Deutscher Verlag der Wissenschaften, 3. Auflage 1976.
Eddy, R.H.
/ Fritsch, R. (1994): The Conics of Ludwig Kiepert: A Comprehensive Lesson in
the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June 1994,
p. 188-205
Euklid (1980): Die Elemente. Nach Heibergs Text aus dem Griechischen bersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft. ISBN 3-534-01488-X
G.-M., F.
(1920/1991): Exercices de Gomtrie. Sixime dition. Tours - Paris: Mame - de
Gigord 1920. Rimpression de la 6e dition publie par Mame et De Gigord en
1920. Sceaux: Gabay 1991. ISBN 2-87647-083-7
Gtzl, Dieter (2006): Besondere Linien im Dreieck – eine Verallgemeinerung. MNU Der mathematische und naturwissenschaftliche Unterricht. 59/8, S. 468-471, ISSN 0025-5866
Haag, Wilfried (2003): Wege zu geometrischen Stzen. Stuttgart: Klett. ISBN 3-12-720120-6
Hauptmann, W. (1995): Erzeugung ãmerkwrdiger PunkteÒ. PM Praxis der Mathematik 37, S. 8
Hoehn, Larry (2001): Extriangles and Excevians. Mathematics Magazine, Vol. 74, No. 5, p. 384-388
Jacobi, C. F. A. (1825): De triangulorum rectilineorum proprietatibus quibusdam nondum satis cognitis. Naumburg.
Kimberling, Clark (1998): Triangle Centers and Central Triangles. Congr. Numer. 129, p. 1 – 295
Klemenz, Heinz (2003): Merkwrdiges im Dreieck. VSMP Bulletin, herausgegeben vom Verein Schweizerischer Mathematik- und Physiklehrer, No 91, S. 16-23
Walser, Hans (1990-1994): Schlusspunkt. Didaktik der Mathematik, 18 (1990) bis 22 (1994), jeweils letzte Heftseite
Walser, Hans (1993): Die Eulersche Gerade als Ort "merkwrdiger Punkte". Didaktik der Mathematik (21), 95-98
Walser, Hans (1994): Eine Verallgemeinerung der Winkelhalbierenden. Didaktik der Mathematik (22), S. 50-56
Walser, Hans (2000): Lattice Geometry and Pythagorean Triangles. ZDM Zentralblatt fr Didaktik der Mathematik. Jahrgang 32, Heft 2, S. 32 - 35
Walser, Hans (2003): Eine Schar von Schnittpunkten im Dreieck. Praxis der Mathematik (2/45), S. 66 - 68
Walser, Hans (2006): 99 Points of Intersection. Examples – Pictures – Proofs. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America. ISBN 0-88385-553-4
Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1
Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.
Wildberger, Norman J. (2010): Chromogeometry. The Mathematical Intelligencer. Volume 32, Number 1. Springer. p. 26-32
Websites
Martin Josefsson: Characterizations of Orthogonal Quadrilaterals (18.06.2016):
http://forumgeom.fau.edu/FG2012volume12/FG201202.pdf
Hans Walser: Appoloniuskreise im Dreieck (22.08.2016):
www.walser-h-m.ch/hans/Miniaturen/A/Apolloniuskreise/Apolloniuskreise.htm
Hans Walser: Orthodiagonale Vierecke (19.06.2016):
www.walser-h-m.ch/hans/Miniaturen/O/Orthodiag_Vierecke/Orthodiag_Vierecke.htm
Hans Walser: Schnittpunkt im Wrfelbild (10.08.2016):
www.walser-h-m.ch/hans/Miniaturen/S/Schnittpunkt2/Schnittpunkt2.htm
Hans Walser: Schnittpunkte in Pythagoras-Beweisen (20.08.2016):
www.walser-h-m.ch/hans/Miniaturen/S/Schnittpunkte_Pythagoras/Schnittpunkte_Pythagoras.htm
Hans Walser: Vierkreisepunkt (01.10.2016}
www.walser-h-m.ch/hans/Miniaturen/V/Vierkreisepunkt/Vierkreisepunkt.htm