Hans Walser

Schnittpunkte 801 - 900

Die Bildsequenzen sind als Bilder ohne Worte konzipiert.

Farbreihenfolge: Dunkelgrün, blau, orange, rot. Nach Bedarf werden auch andere Farben verwendet.

Die drei kleinen Bilder im Querstreifen deuten die Entstehung der Gesamtfigur an.

Gegebenenfalls finden sich unterhalb der Figur Literaturangaben oder Hinweise auf Anregungen, die zu diesen Figuren geführt haben.

Letzte Änderung 29. Mai 24

Schnittpunkt 801

Frégier

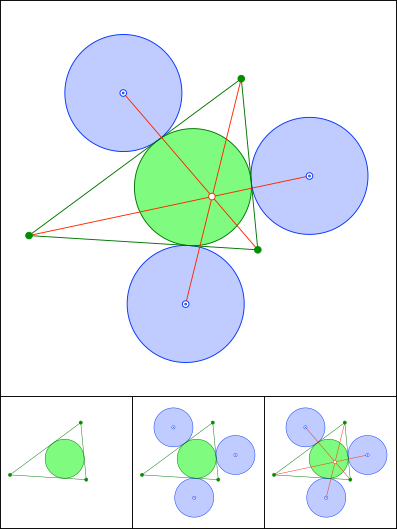
Schnittpunkt 802

Frégier

Schnittpunkt 803

Frégier

Schnittpunkt 804

Frégier

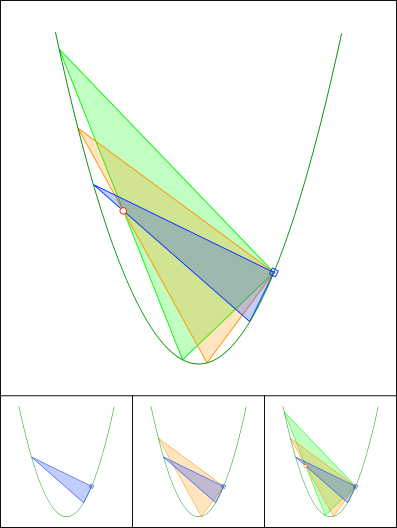
Schnittpunkt 805

Frégier

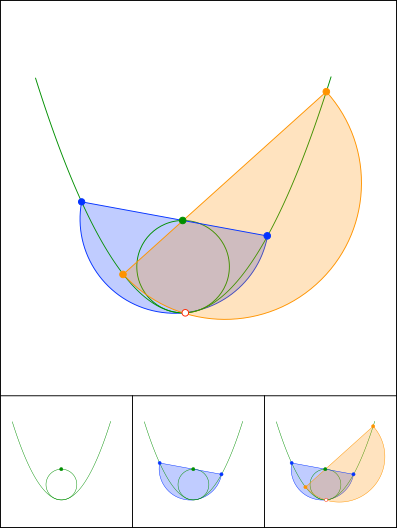
Schnittpunkt 806

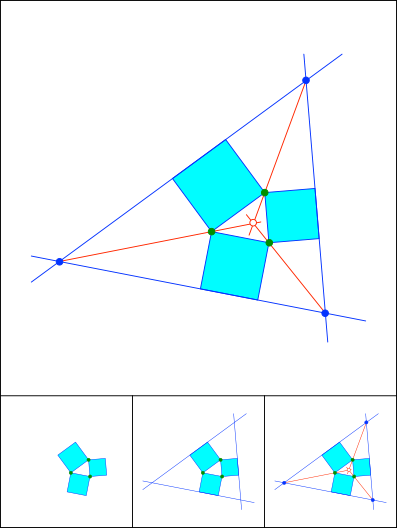
Lemoine / Grebe

Schnittpunkt 807

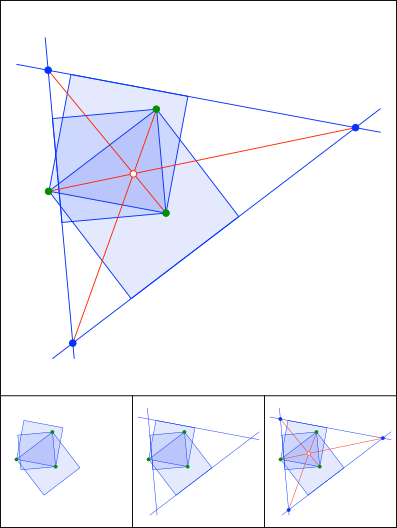
Lemoine / Grebe

Schnittpunkt 808

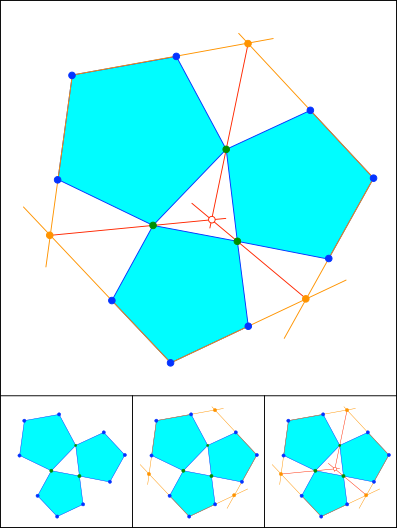
Lemoine

Schnittpunkt 809

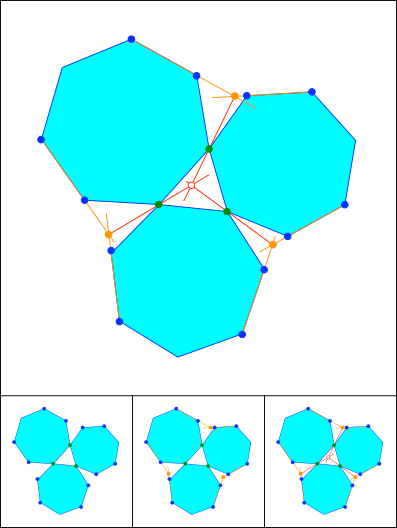
Lemoine

Schnittpunkt 810

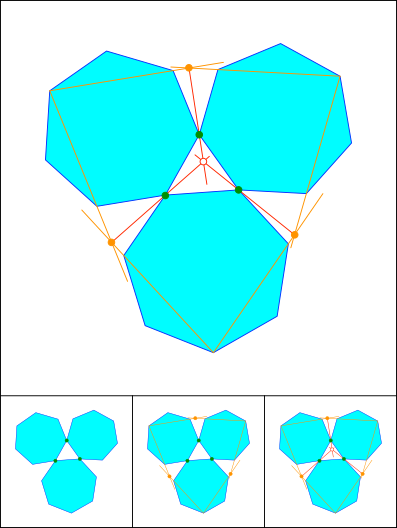
Schnittpunkt 811

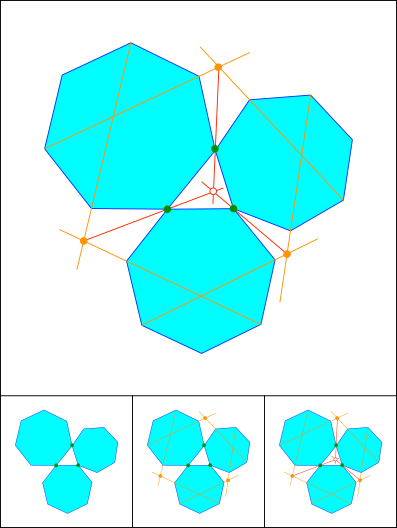
Schnittpunkt 812

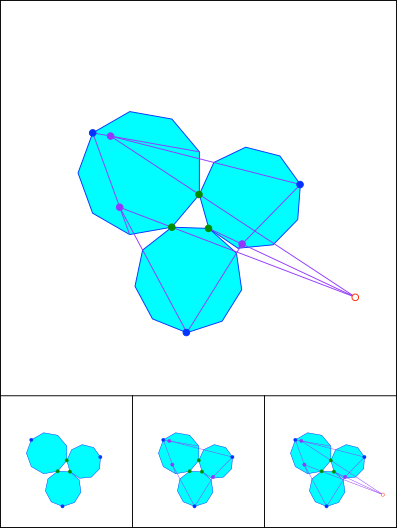
Schnittpunkt 813

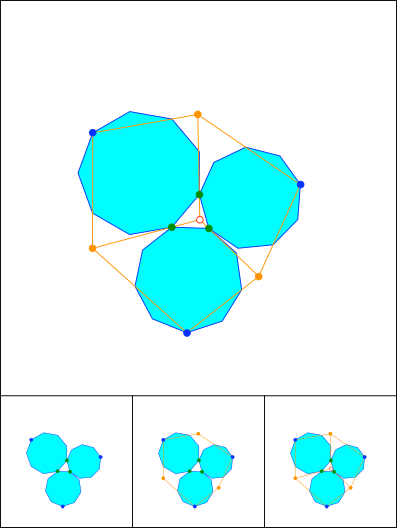
Schnittpunkt 814

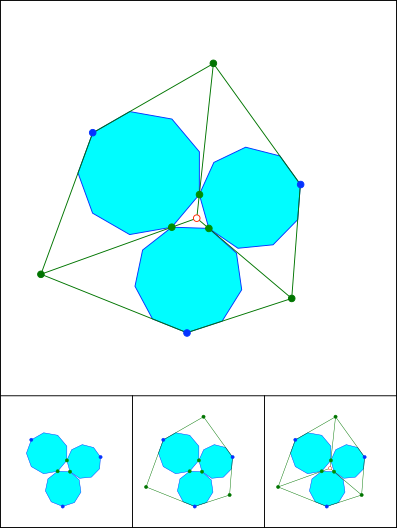
Schnittpunkt 815

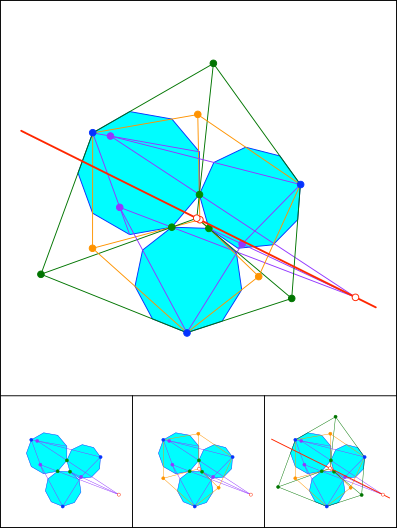
Synopsis von 812, 813 und 814. Lemoine-Gerade

Schnittpunkt 816

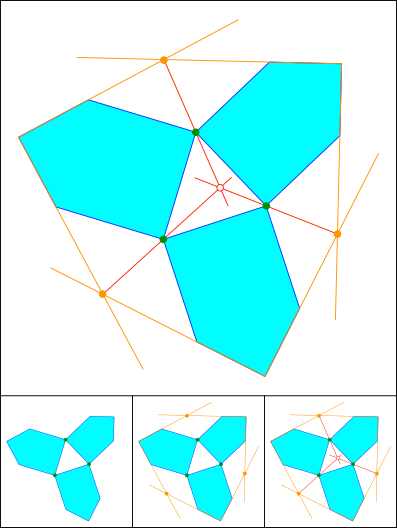
Schaffe, schaffe, Häusle baue

Schnittpunkt 817

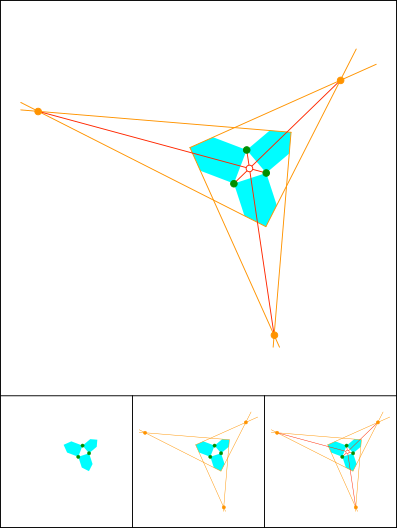
Schnittpunkt 818

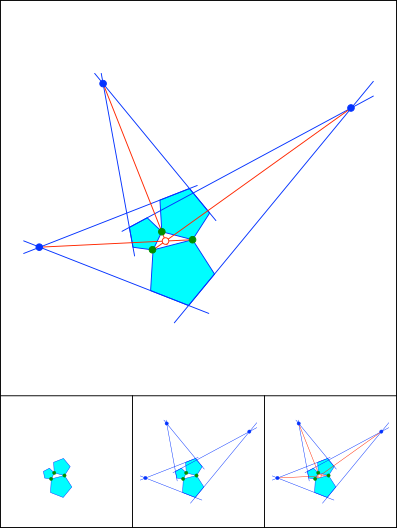
Schnittpunkt 819

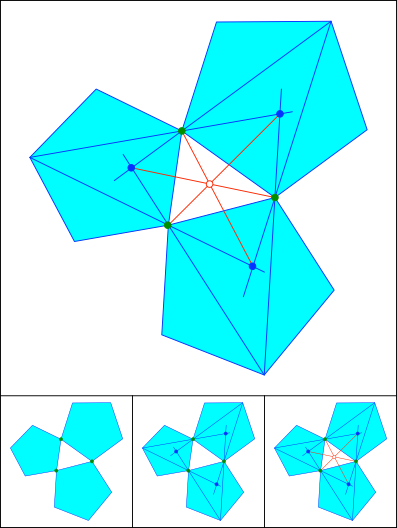
Schnittpunkt 820

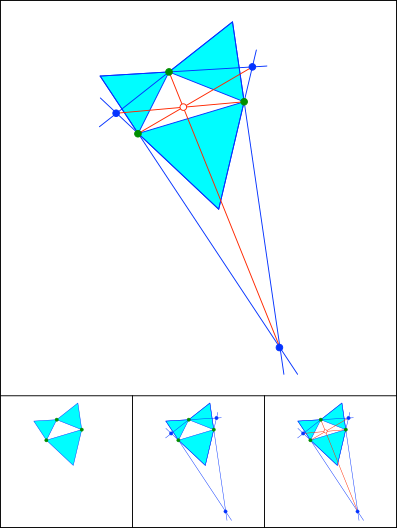
Schnittpunkt 821

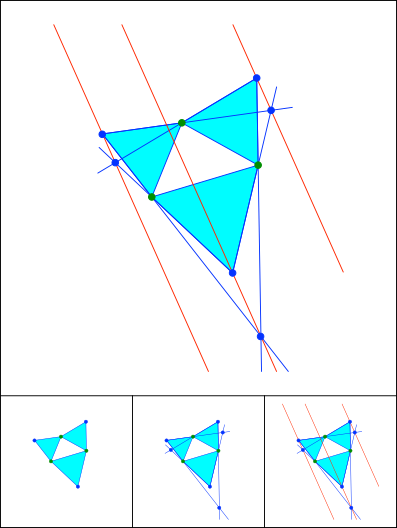
Schnittpunkt im Unendlichen. Parallele Geraden

Schnittpunkt 822

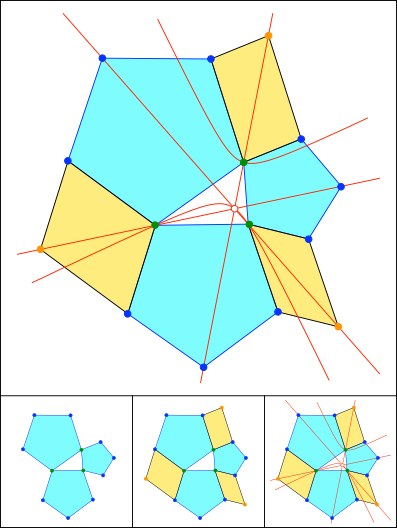
Schnittpunkt 823

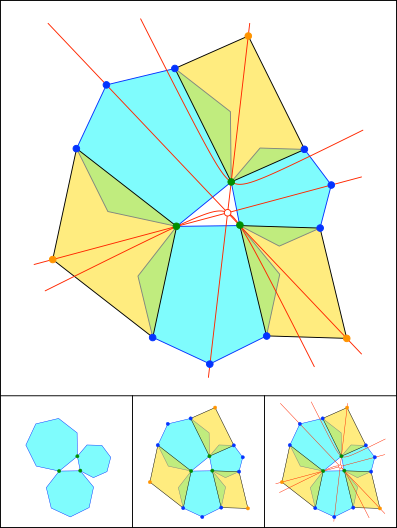
Schnittpunkt 824

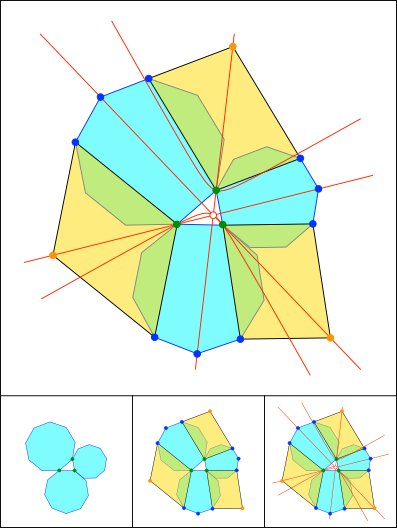
Schnittpunkt 825

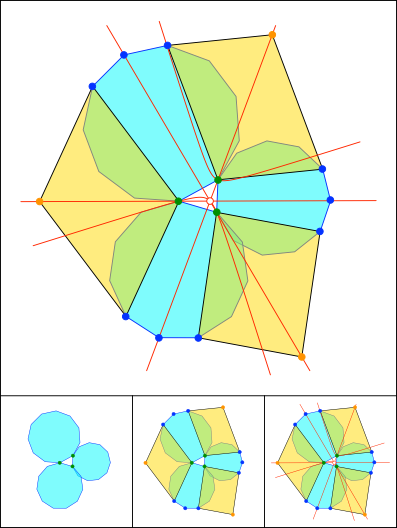
Schnittpunkt 826

Archimedische Spirale

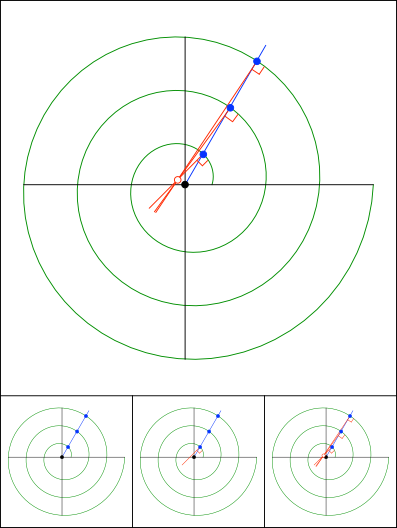
Schnittpunkt 827

Archimedische Spirale

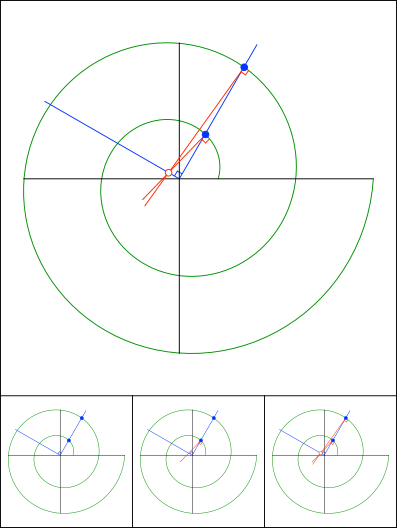
Schnittpunkt 828

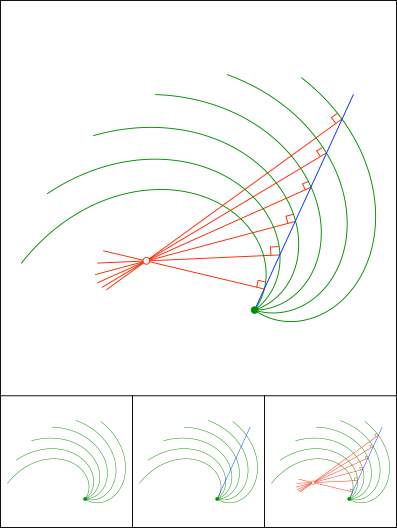
Verdrehte archimedische Spiralen

Schnittpunkt 829

Sechs Kreise

Schnittpunkt 830

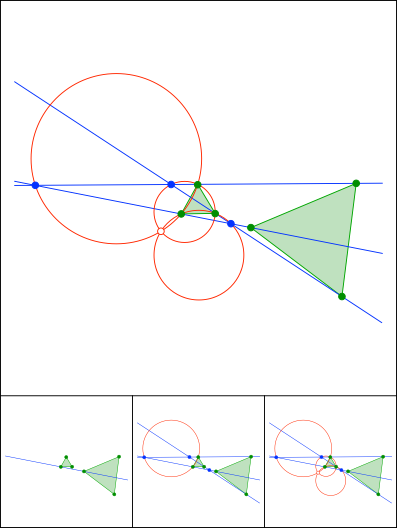
Drei Kreise

Schnittpunkt 831

Hartmut Müller-Sommer. Eulergeraden der Ankreisdreiecke

Schnittpunkt 832

Hartmut Müller-Sommer. Noch mehr Eulergeraden

Schnittpunkt 833

Schnittpunkt 834

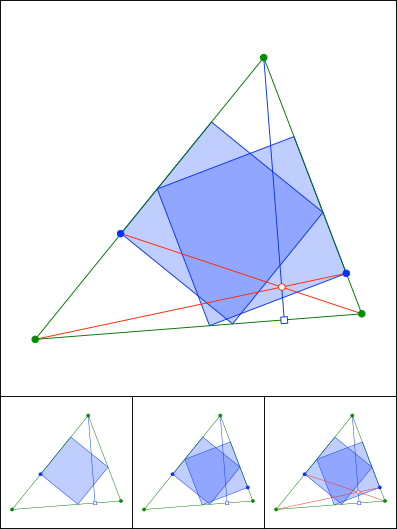
Schnittpunkt 835

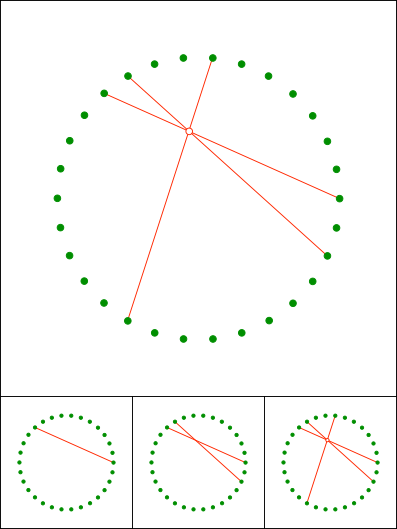
Gallin & Klemenz, 2021

Schnittpunkt 836

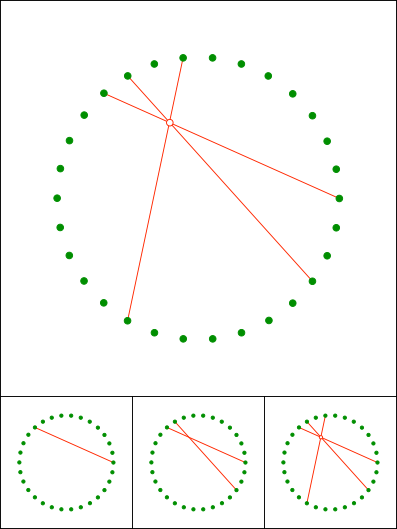
Gallin & Klemenz, 2021

Schnittpunkt 837

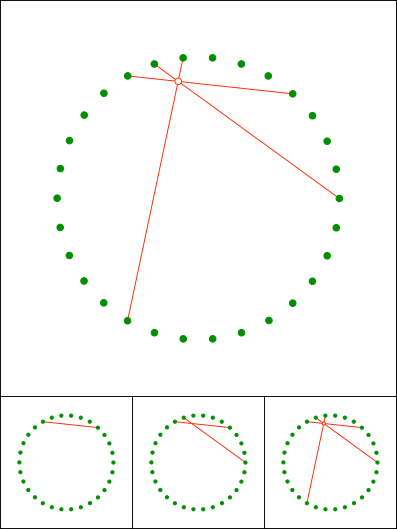
Gallin & Klemenz, 2021

Schnittpunkt 838

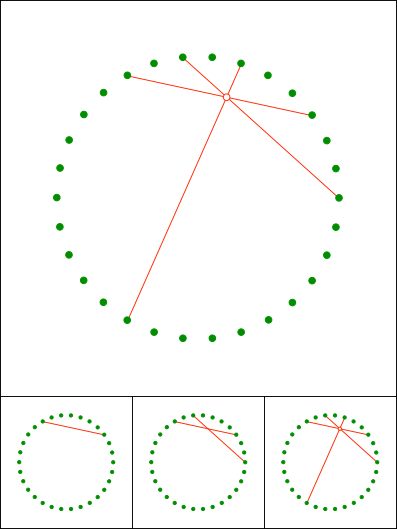
Gallin & Klemenz, 2021

Schnittpunkt 839

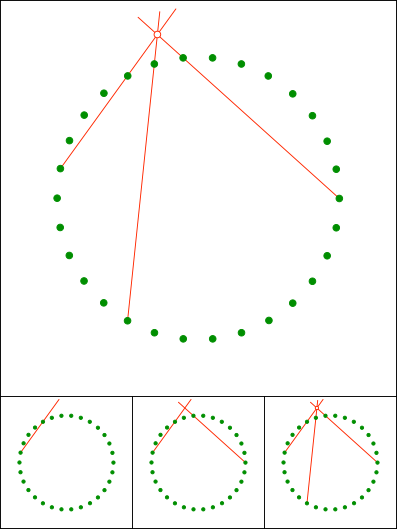
Gallin & Klemenz, 2021

Schnittpunkt 840

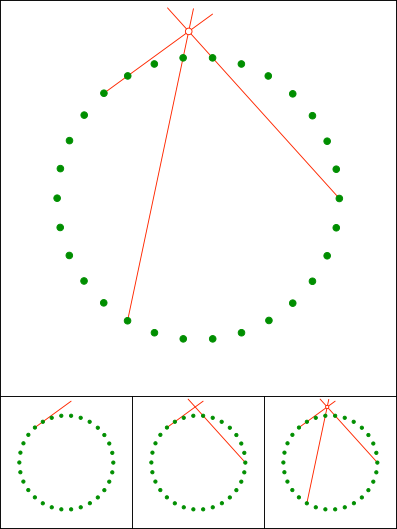
Gallin & Klemenz, 2021

Schnittpunkt 841

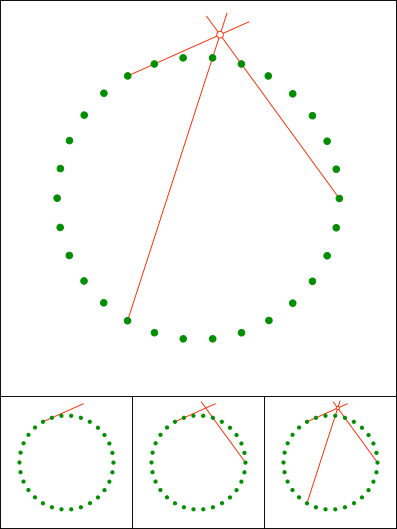
Gallin & Klemenz, 2021

Schnittpunkt 842

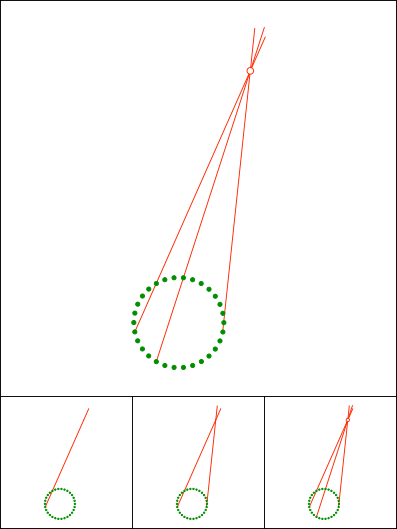
Gallin & Klemenz, 2021

Schnittpunkt 843

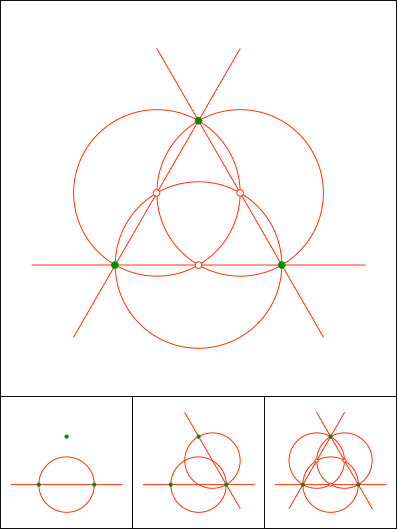
Schnittpunkt 844

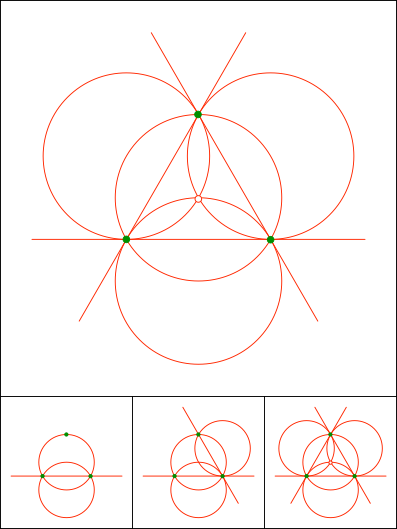
Schnittpunkt 845

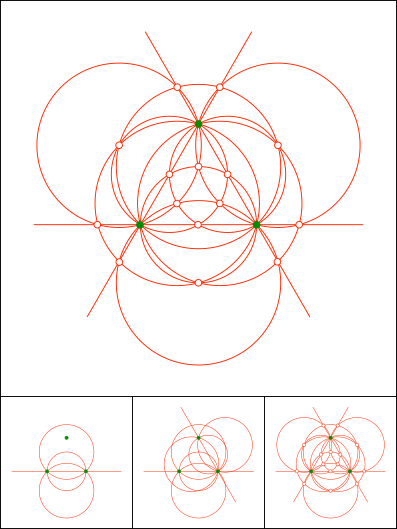
Schnittpunkt 846

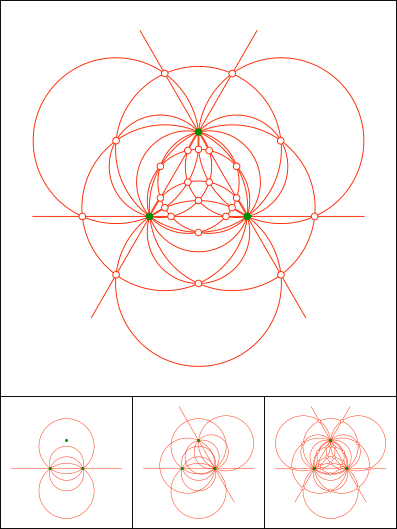
Schnittpunkt 847

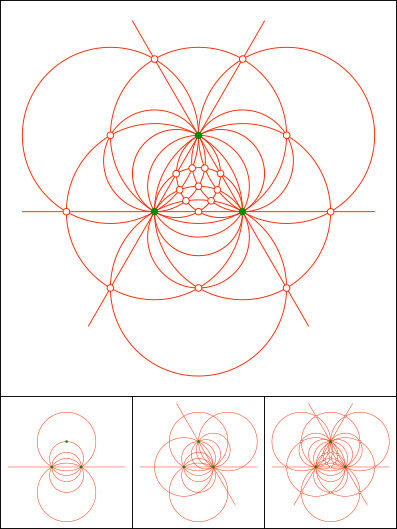
Schnittpunkt 848

Schnittpunkt 849

Schnittpunkt 850

Schnittpunkt 851

Schnittpunkt 852

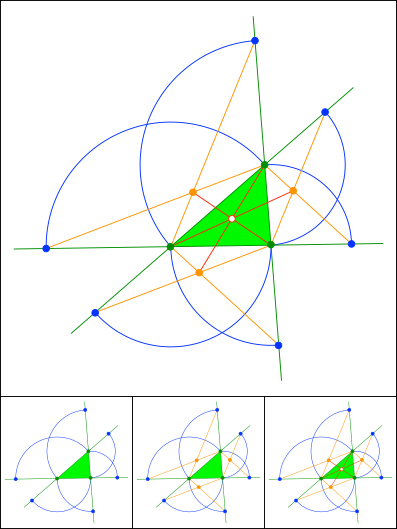
Thomas Jahre, Chemnitz

Schnittpunkt 853

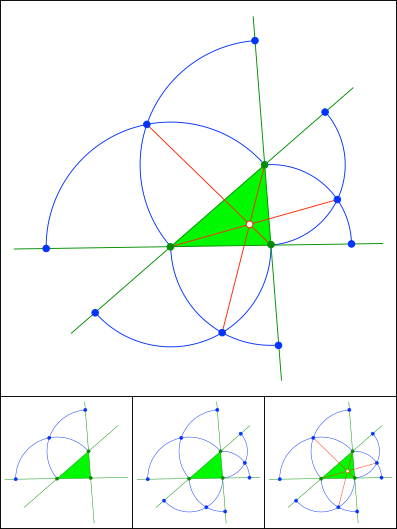
Fermat-Punkt

Schnittpunkt 854

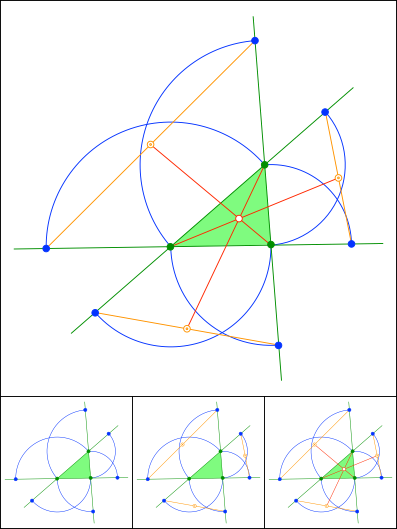
Thomas Jahre, Chemnitz

Schnittpunkt 855

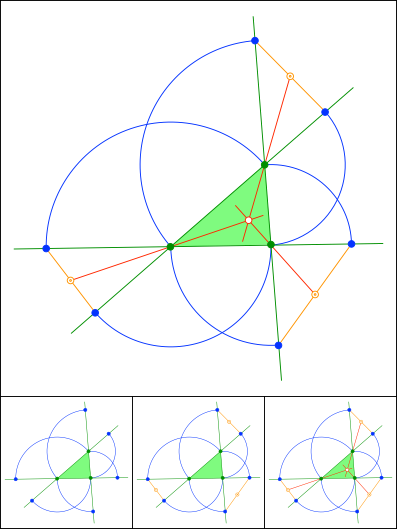
Thomas Jahre, Chemnitz

Schnittpunkt 856

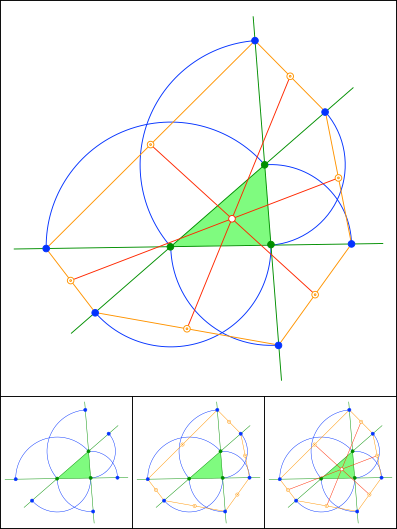
Thomas Jahre, Chemnitz

Schnittpunkt 857

Thomas Jahre, Chemnitz

Schnittpunkt 858

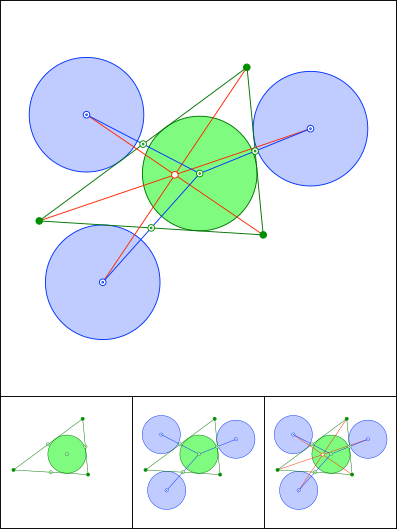
Schnittpunkt 859

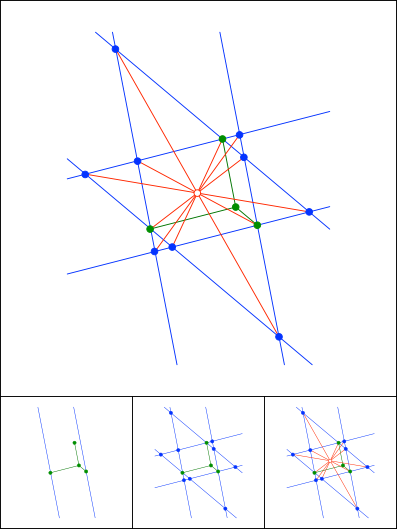
Schnittpunkt 860

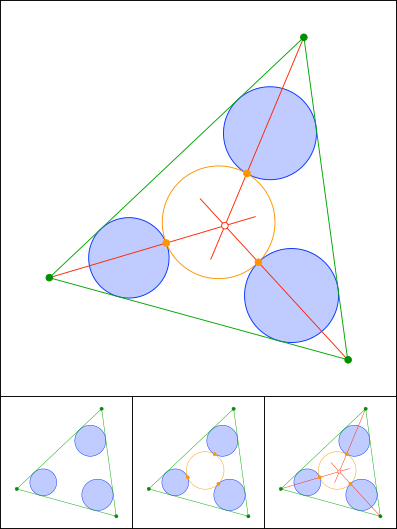
Schnittpunkt 861

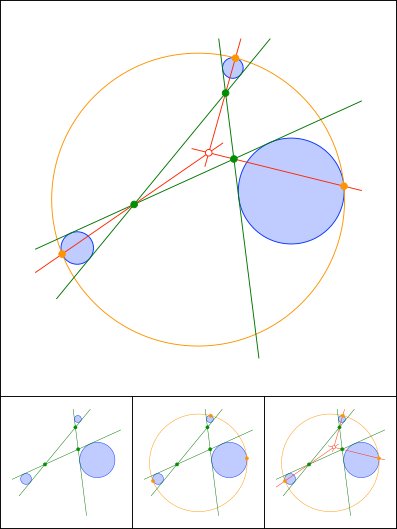
Schnittpunkt 862

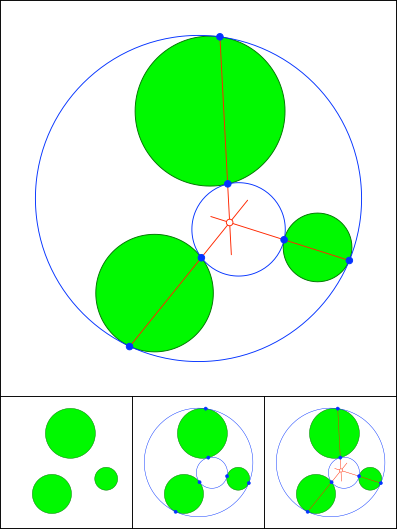
Schnittpunkt 863

Schnittpunkt 864

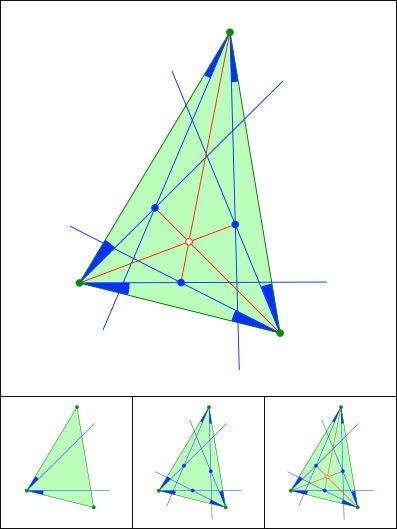
Gleiche Winkelanteile

Schnittpunkt 865

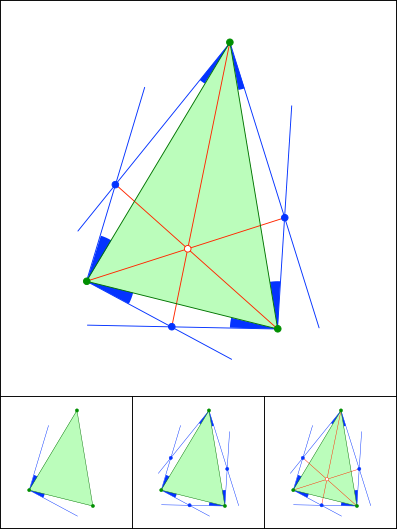
Gleiche Winkelanteile

Schnittpunkt 866

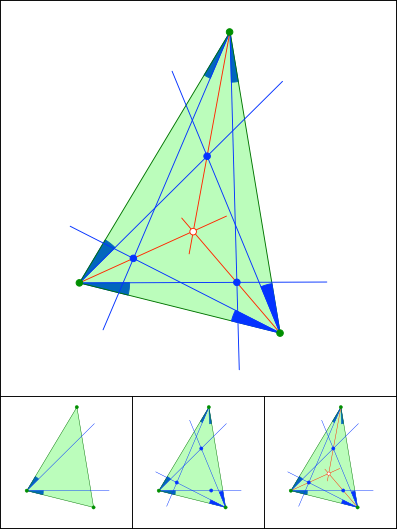
Gleiche Winkelanteile

Schnittpunkt 867

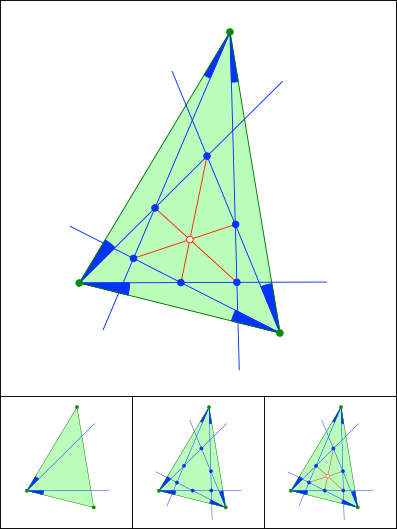
Gleiche Winkelanteile

Schnittpunkt 868

Ortsbogen

Schnittpunkt 869

Ortsbogen

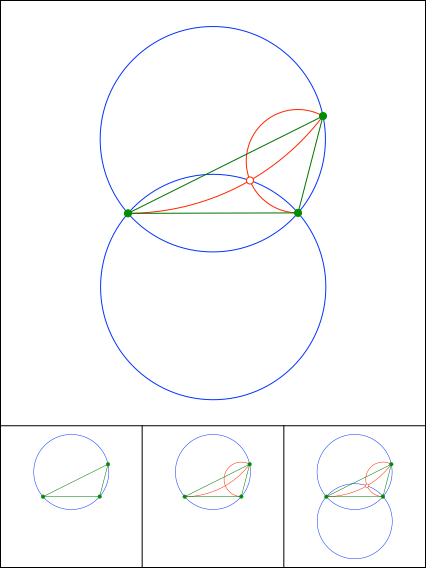
Schnittpunkt 870

Schnittpunkt

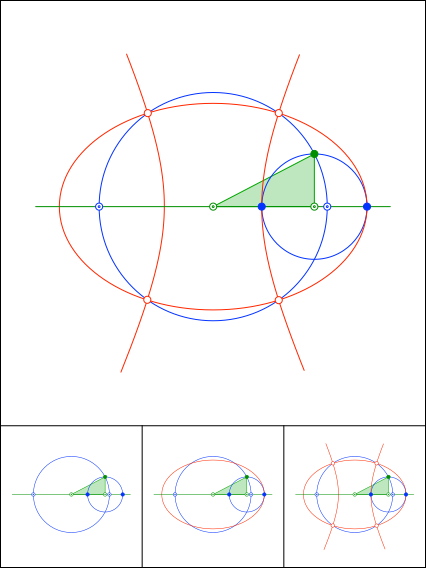
Schnittpunkt 871

Schnittpunkt

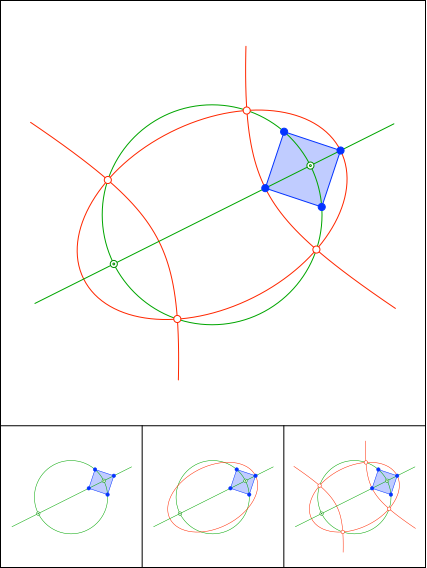
Schnittpunkt 872

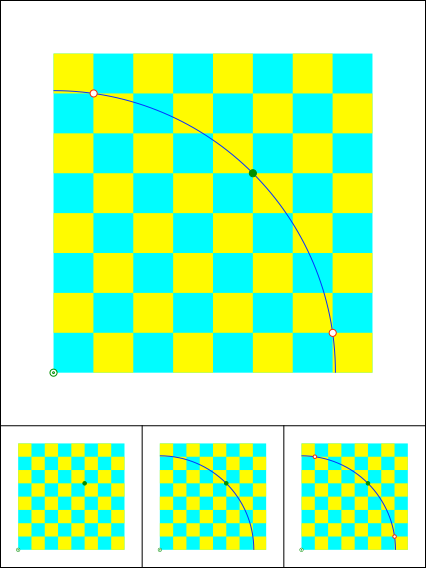
Schachbrett und Viertelkreis

Schnittpunkt 873

Schachbrett und Kreisbogen

Schnittpunkt 874

Großes Schachbrett und Viertelkreis

Schnittpunkt 875

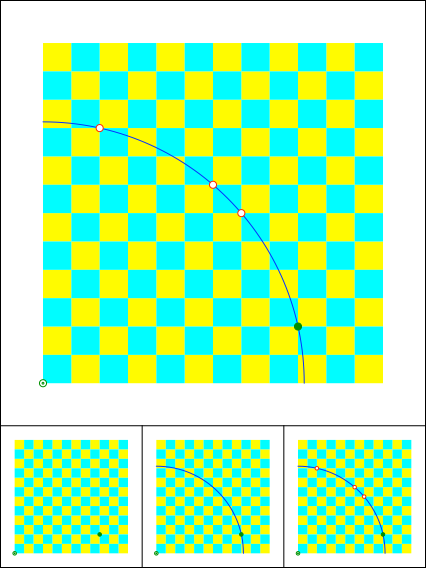
Großes Schachbrett und Viertelkreis

Schnittpunkt 876

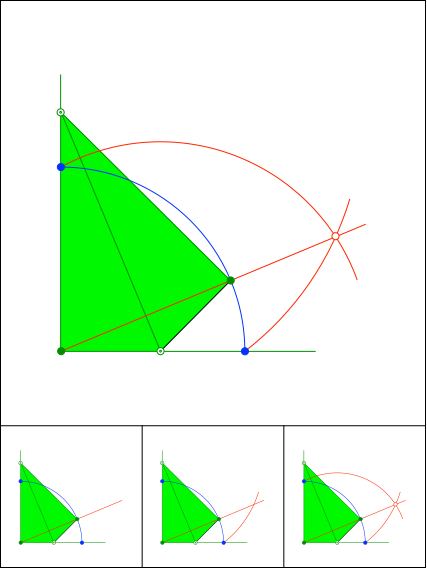
Drachenviereck mit rechten Winkeln

Schnittpunkt 877

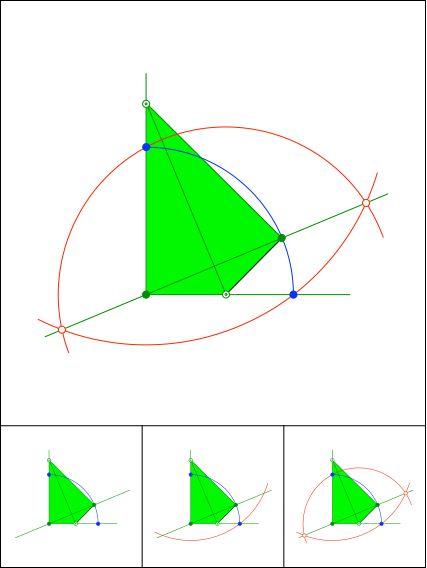
Drachenviereck mit rechten Winkeln

Schnittpunkt 878

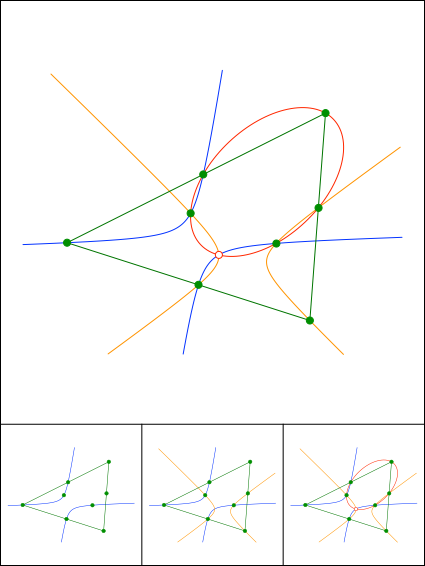
Miquel-Verallgemeinerung

Schnittpunkt 879

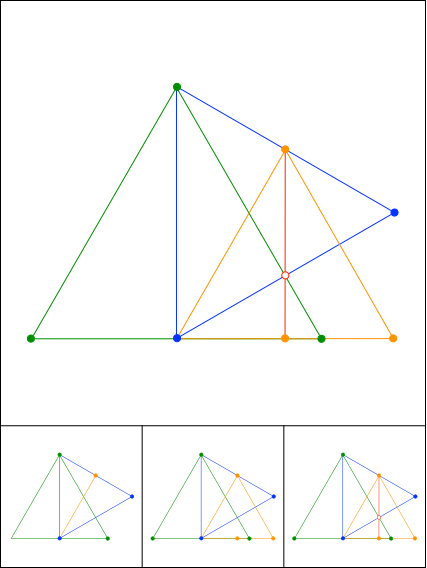
Folge von gleichseitigen Dreiecken

Schnittpunkt 880

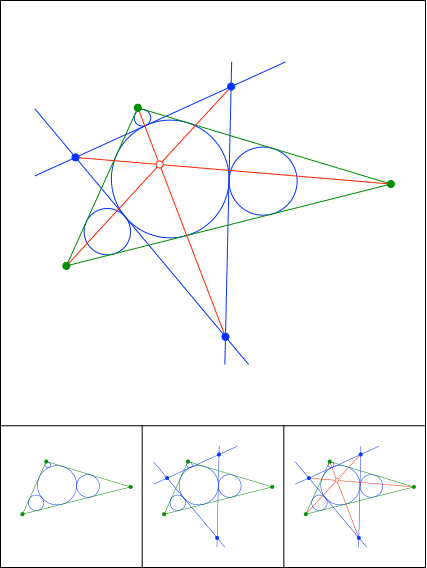
Schnittpunkt 881

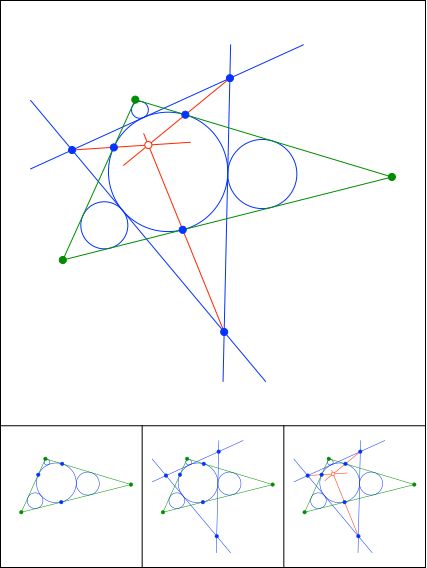
Schnittpunkt 882

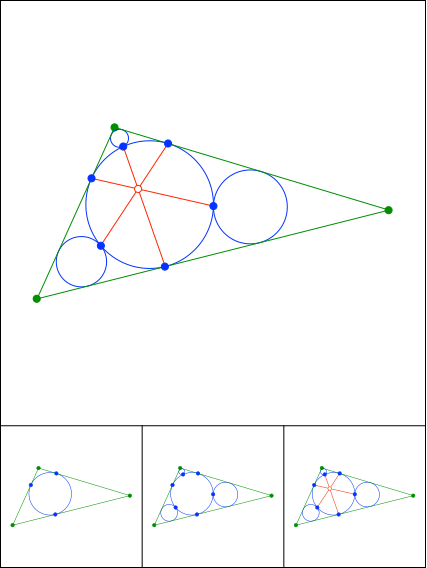
Schnittpunkt 883

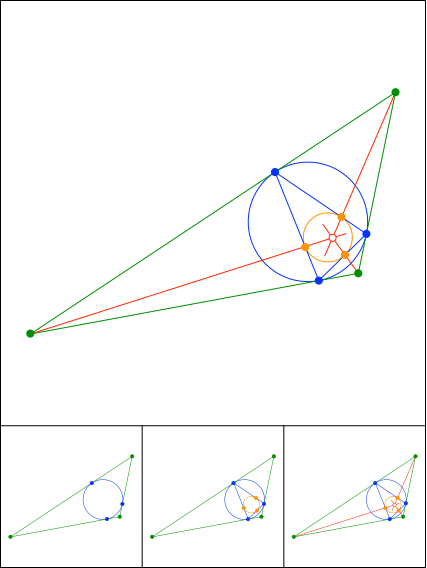
Schnittpunkt 884

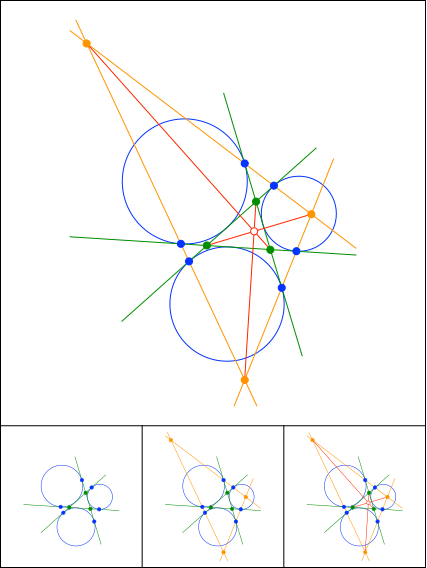
Schnittpunkt 885

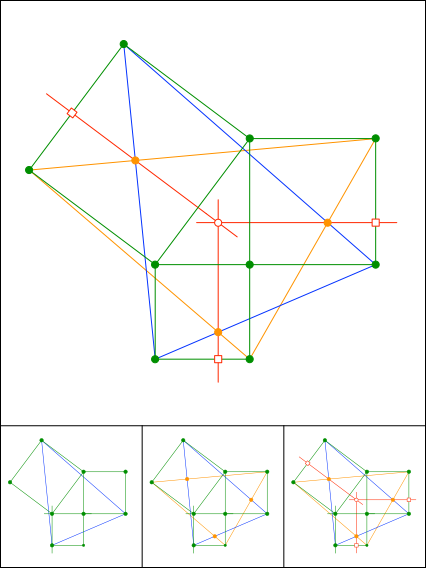
Schnittpunkt 886

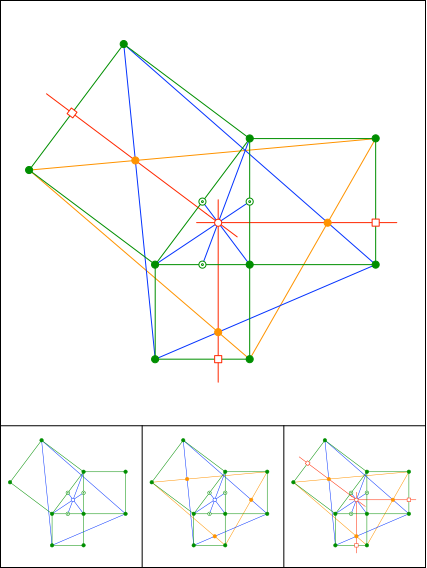
Schnittpunkt 887

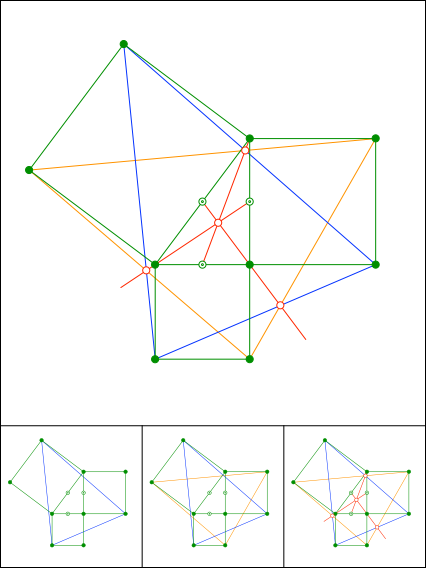
Schnittpunkt 888

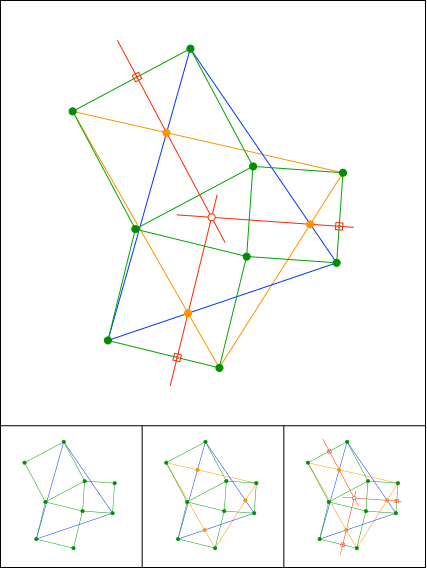
Schnittpunkt 889

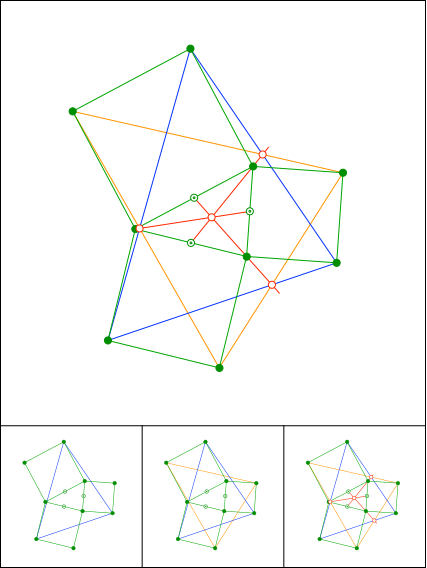
Schnittpunkt 890

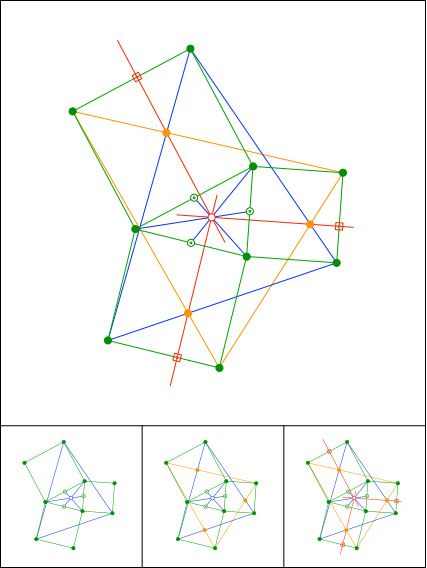
Schnittpunkt 891

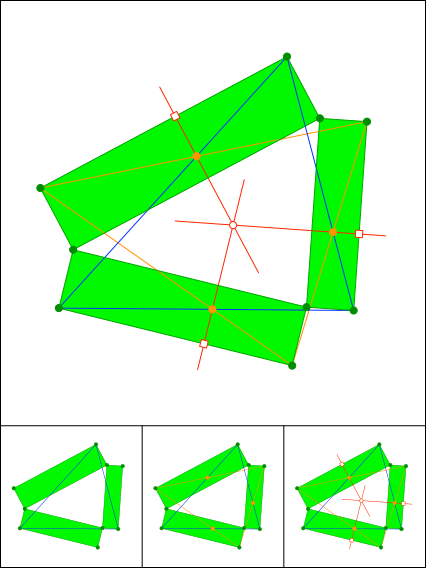
Schnittpunkt 892

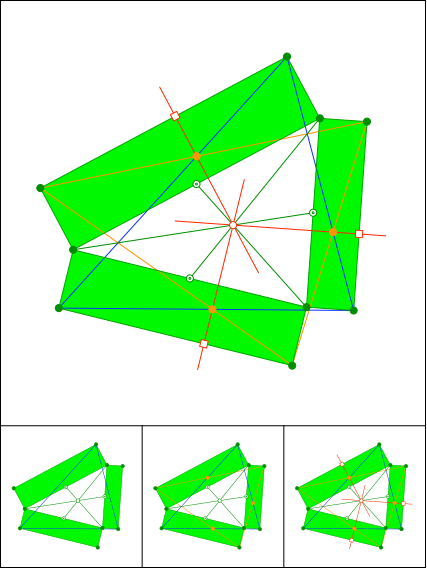
Schnittpunkt 893

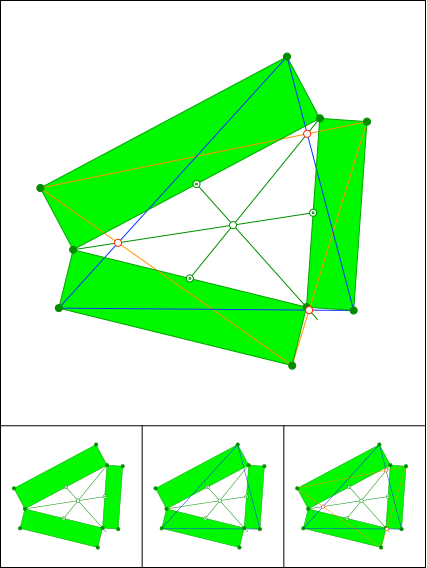
Schnittpunkt 894

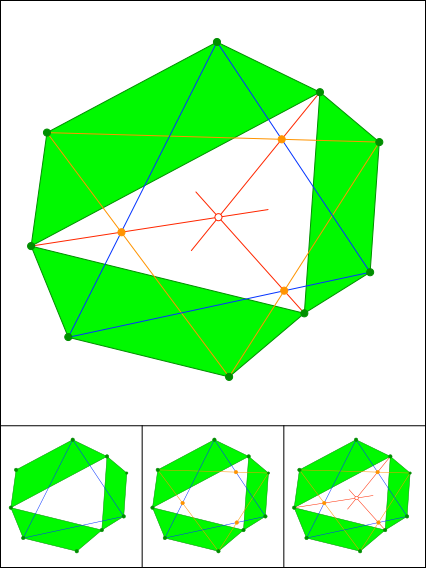
Gleichschenklige Trapeze

Schnittpunkt 895

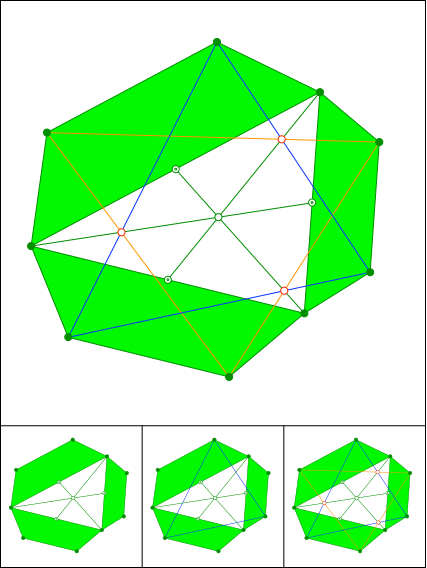
Gleichschenklige Trapeze

Literatur

Baptist, Peter (1992): Die Entwicklung der neueren Dreiecksgeometrie. Mannheim: B.I.Wissenschaftsverlag. ISBN 3-411-15661-9

Donath, Emil (1976): Die merkwürdigen Punkte und Linien des ebenen Dreiecks. Berlin: Deutscher Verlag der Wissenschaften, 3. Auflage 1976.

Eddy, R.H. / Fritsch, R. (1994): The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June 1994, p. 188-205

Euklid (1980): Die Elemente. Nach Heibergs Text aus dem Griechischen übersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft. ISBN 3-534-01488-X

G.-M., F. (1920/1991): Exercices de Géométrie. Sixième édition. Tours - Paris: Mame - de Gigord 1920. Réimpression de la 6e édition publieé par Mame et De Gigord en 1920. Sceaux: Gabay 1991. ISBN 2-87647-083-7

Gallin, Peter und Klemenz, Heinz (2021): Die 6°-12°-18°-Punkte im gleichseitigen Dreieck. VSMP-Bulletin, No 147, September 2021, S. 12-14.

Götzl, Dieter (2006): Besondere Linien im Dreieck – eine Verallgemeinerung. MNU Der mathematische und naturwissenschaftliche Unterricht. 59/8, S. 468-471, ISSN 0025-5866

Haag, Wilfried (2003): Wege zu geometrischen Sätzen. Stuttgart: Klett. ISBN 3-12-720120-6

Hauptmann, W. (1995): Erzeugung „merkwürdiger Punkte“. PM Praxis der Mathematik 37, S. 8

Hoehn, Larry (2001): Extriangles and Excevians. Mathematics Magazine, Vol. 74, No. 5, p. 384-388

Jacobi, C. F. A. (1825): De triangulorum rectilineorum proprietatibus quibusdam nondum satis cognitis. Naumburg.

Kimberling, Clark (1998): Triangle Centers and Central Triangles. Congr. Numer. 129, p. 1 – 295

Klemenz, Heinz (2003): Merkwürdiges im Dreieck. VSMP Bulletin, herausgegeben vom Verein Schweizerischer Mathematik- und Physiklehrer, No 91, S. 16-23

Reuleaux, F. (1875): Lehrbuch der Kinematik. Braunschweig: Vieweg.
https://ia700409.us.archive.org/29/items/lehrbuchderkine01reulgoog/lehrbuchderkine01reulgoog.pdf

Strick, Heinz Klaus (2017): Mathematik ist schön. Anregungen zum Anschauen und Erforschen für Menschen zwischen 9 und 99 Jahren. Berlin: Springer. ISBN 978-3-662-53729-9.

Walser, Hans (1990-1994): Schlusspunkt. Didaktik der Mathematik, 18 (1990) bis 22 (1994), jeweils letzte Heftseite

Walser, Hans (1993): Die Eulersche Gerade als Ort "merkwürdiger Punkte". Didaktik der Mathematik (21), 95-98

Walser, Hans (1994): Eine Verallgemeinerung der Winkelhalbierenden. Didaktik der Mathematik (22), S. 50-56

Walser, Hans (2000): Lattice Geometry and Pythagorean Triangles. ZDM Zentralblatt für Didaktik der Mathematik. Jahrgang 32, Heft 2, S. 32 - 35

Walser, Hans (2003): Eine Schar von Schnittpunkten im Dreieck. Praxis der Mathematik (2/45), S. 66 - 68

Walser, Hans (2006): 99 Points of Intersection. Examples – Pictures – Proofs. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America. ISBN 0-88385-553-4

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.

Weiss, Gunter (2018): Thales-3D mit der Idee von M. Frégier. IBDG, Informationsblätter der Geometrie. 37. 2/2018. 30-37.

Wildberger, Norman J. (2010): Chromogeometry. The Mathematical Intelligencer. Volume 32, Number 1. Springer. p. 26-32

Websites

Martin Josefsson: Characterizations of Orthogonal Quadrilaterals (18.06.2016):

http://forumgeom.fau.edu/FG2012volume12/FG201202.pdf

Hans Walser: Miquel-Verallgemeinerung (26.07.2023)

http://www.walser-h-m.ch/hans/Miniaturen/M/Miquel-Verallgemeinerung/Miquel-Verallgemeinerung.html

Hans Walser: Ortsbogen (24.05.2022)

http://www.walser-h-m.ch/hans/Miniaturen/O/Ortsbogen2/Ortsbogen2.html

Hans Walser: Lotschnittpunkt (16. 11. 2020)

http://www.walser-h-m.ch/hans/Miniaturen/L/Lotschnittpunkt2/Lotschnittpunkt2.htm

Hans Walser: Lotschnittpunkt (31.10.2020)