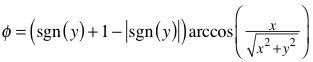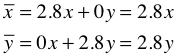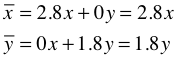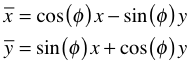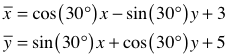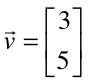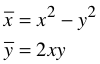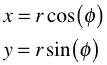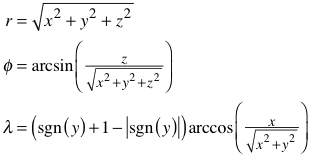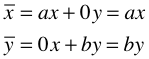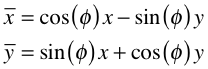Von der
Schule her kennen wir das klassische kartesische Koordinatensystem in der
Ebene. Die positive x-Achse muss um
+90° gedreht werden, um auf die positive y-Achse
zu gelangen.
Koordinatensystem
Es gibt
allerdings auch Situationen, wo der Ursprung links oben ist, so dass die y-Achse nach unten verläuft (in den
meisten Tabellen ist es so).
Die
geografischen Koordinaten werden traditionellerweise mit geografischer Länge
und geografischer Breite bezeichnet. Dies widerspricht allerdings den
zugeordneten Maßeinheiten (Degree oder Radian), welche für Winkel gebräuchlich sind.
Geografische Länge und Breite
Auf der
klassischen Plattkarte können diese Koordinaten als Längen
wie die x- und y-Koordinaten abgetragen werden. Es spielt auch
keine Rolle, ober wir „unten durch“ oder „oben durch“ arbeiten.
Unten durch und oben durch
Auf der
Erdkugel sieht die Situation aber anders aus.
Auf der Erdkugel
Die
geografischen Koordinaten sind in Wirklichkeit Winkel.
Die
geografische Länge ist der Drehwinkel der Drehung der Meridiane um die
Erdachse. Die geografische Breite hat mit dem Kegel zu tun, der seine Spitze im
Erdmittelpunkt hat und dessen Leitkreis der zugeordnete Breitenkreis ist. Die
geografische Breite ist der Komplementwinkel des halben Öffnungswinkels des
Kegels auf 90°.
Geografische Länge und Breite als Winkel
Geografische Länge und Breite
Im Raum
brauchen wir drei Achsen. Üblicherweise wird ein Rechtssystem verwendet. Durch
Einzeichnen einer Hilfsfigur, zum Beispiel des Einheitswürfels oder der
Erdkugel, kann auch in einer 2d-Darstellung entschieden werden, ob es sich um
ein Rechtssystem oder ein Linkssystem handelt.
Koordinatensystem im Raum. Rechtssystem
Koordinatensystem mit Erdkugel
Die
folgende Abbildung zeigt ein Linkssystem. Wir haben eine Untersicht oder
Froschperspektive
Linkssystem
PovRay verwendet ebenfalls ein Linkssystem.
Die z-Achse geht nach hinten.
Linkssystem von PovRay
Polarkoordinaten
sind sozusagen „natürliche“ Koordinaten zur Orientierung: „In dieser Richtung
und so weit“.
Es ist 
und 
.
Polarkoordinaten
Die
Umrechung von Polarkoordinaten auf kartesische Koordinaten ist einfach:
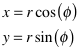
Für die
Umrechung von kartesischen Koordinaten auf Polarkoordinaten ist der
Polarabstand r einfach:
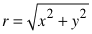
Hingegen
macht der Polarwinkel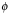 
Probleme, es
braucht bei Verwendung des Arkustangens Fallunterscheidungen:
Mit dem
Arkuskosinus braucht es nur zwei Fallunterscheidungen:
Ohne
Fallunterscheidung geht es unter Verwendung der Signum-Funktion
(Vorzeichenfunktion):
Signum-Funktion
Einige
Programmiersprachen verwenden die Schreibweise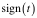 
für die
Signum-Funktion.
Damit können
wir den Polarwinkel wie folgt berechnen:
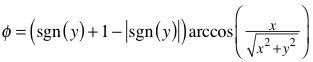
Natürlich
haben wir lediglich die Fallunterscheidung in die Signum-Funktion versteckt.
Die Kugelkoordinaten oder sphärischen Koordinaten orientieren sich
an den geografischen Koordinaten. Es ist:
, 
, 
.
Kugelkoordinaten
Für die
Umrechnung in kartesische Koordinaten ergänzen wir die Figur:
Umrechung in kartesische Koordinaten
Wir
erhalten:
In der
umgekehrten Richtung gilt:
Wir haben
beim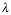 
das Theater mit
den Fallunterscheidungen.
Beispiel:
Welche Kugelkoordinaten hat der Punkt P
der folgenden Abbildung?
Kugelkoordinaten des Punktes P?
Der Punkt
hat die kartesischen Koordinaten P(1,1,1). Daraus ergibt sich:
Wir gehen
aus von einer Plattkarte, von der wir annehmen, dass das Bild des Äquators 40
cm messe.
Plattkarte
Am
Äquator haben wir dann in West-ost-Richtung einen Maßstab 1 : 100'000'000.
Denselben Maßstab haben wir auch auf jedem Meridian in Süd-Nord-Richtung.
Auf den
Breitenkreisen ist die Situation aber anders. Der Breitenkreis für 60°N ist in
Wirklichkeit nur halb so lang wie der Äquator, aber auf unseren Karte gleich
lang gezeichnet.
Daher ist
sein Maßstab in West-Ost-Richtung doppelt so groß, also 1 : 50'000'000.
Je näher
wir an die Pole kommen, umso größer wird der Maßstab in West-Ost-Richtung. An den Polen selber ist er 1 : 0, also
„unendlich“. In einem Abstand von (in Wirklichkeit) 6.37cm vom Nordpol ist der
Maßstab tatsächlich 1 : 1. Dies ist auf der geografischen Breite 89°59’59.998“.
Wenn wir
uns auf der Erde eine runden Swimming-Pool vorstellen, den wir mit-kartografieren, wird sein Bild in der West-Ost-Richtung
auseinandergezogen, und zwar umso stärker, je mehr wir uns den Polen nähern.
Die Bildkurve kann gut durch eine Ellipse dargestellt werden. Damit das Bild
des sehr kleinen Swimming-Pools auf der Karte überhaupt sichtbar ist, wird es
noch gezoomt.
Eine
solche Ellipse heißt Verzerrungsellipse oder Tissot-Indikatrix.
Plattkarte mit Verzerrungsellipsen
Verzerrungsellipsen
Orthografische Projektion mit
Verzerrungsellipsen
Herzkarte mit Verzerrungsellipsen
Die Idee der Verzerrungsellipse basiert auf
einem „kleinen“ Kreis. Ein Swimming-Pool im Garten ist ja im Verhältnis zur
Erdkugel sehr klein. Mathematisch arbeitet man mit einem infinitesimal kleinen
Kreis, dessen Bild dann auf der Karte vergrößert wird.
Echte Kreise (Distanzkreise, Radius gemessen
auf der Kugeloberfläche) sind auf der Plattkarte nicht ellipsenförmig.
Distanzkreise auf der Plattkarte
Wir
arbeiten mit den Abbildungsgleichungen:
Das
heißt, dass jedem Punkt 
ein Bildpunkt 
zugeordnet
wird.
Beispiel:
Sehr oft
werden die Abbildungsgleichungen in Matrixform dargestellt:
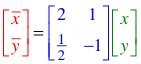
Kurzform:
In
unserem Beispiel:
Bilder
der Einheitsvektoren:
Bilder der Einheitsvektoren
Die
Spalten der Abbildungsmatrix sind die Bilder der Einheitsvektoren.
Bild des Einheitsquadrates
Die
Determinante der Abbildungsmatrix:
Die
Determinante der Abbildungsmatrix ist betragsmäßig der Flächenmaßstab. Das Vorzeichen der Determinante gibt an, ob die
Orientierung geändert wird.
Bild eines Quadratrasters
Im Raster
können wir grafisch verifizieren, dass zum Beispiel:
Statt
einzelner Punkte können wir eine ganze Figur abbilden:
Urbild und Bild
Wir
strecken in jeder Richtung um den gleichen Faktor.
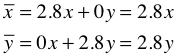
Die
Abbildungsmatrix ist eine so genannte Diagonalmatrix mit lauter gleichen
Elementen in der Diagonalen:
Zentrische Streckung
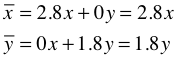
Die
Abbildungsmatrix ist eine Diagonalmatrix:
Unterschiedliche Skalierungen
Aus
Kreisen werden Ellipsen (so genannte Verzerrungsellipsen oder Tissot-Indikatrizen).
Für eine
Rotation um den Ursprung um den Winkel 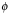benötigen wir
die Abbildungsgleichungen:
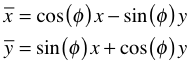
Wir haben
die Abbildungsmatrix:
Bild der
Einheitsvektoren:
Rotation: Bild der Einheitsvektoren
Beispiel:
Rotation
Bei allen
bisherigen Abbildungen blieb der Ursprung ortsfest, war also ein so genannter Fixpunkt. Wenn wir das ändern wollen,
müssen wir in den Abbildungsgleichungen zusätzliche additive Summanden
einführen.
Das
folgende Beispiel erläutert die Situation für die Abbildungsgleichungen:
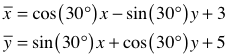
Wir haben
einen Translationsvektor:
.
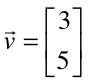Rotation und Translation
Eine
reine Translation ohne weitere Transformation ist gegeben durch:
Wir haben
den Translationsvektor
Transformationen
können verknüpft werden, indem der Output der ersten Transformation als Input
der zweiten Transformation verwendet wird.
Die neue
Abbildungsmatrix ist das Produkt der beiden einzelnen Abbildungsmatrizen.
Die
Reihenfolge der Verknüpfung ist in der Regel nicht vertauschbar.
Abbildungsgleichungen:
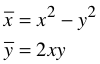
Quadratische Abbildung
Im Raum
gibt es Rechtssysteme und Linkssysteme.
Polarkoordinaten
—> kartesische Koordinaten:
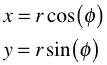
Umgekehrte
Richtung:
Kugelkoordinaten
—> kartesische Koordinaten:
Umgekehrte
Richtung:
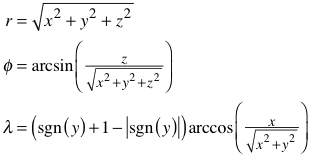
Translation:
Skalierung
mit gleichen Faktoren:
Skalierung
mit ungleichen Faktoren:
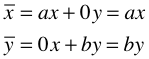
Rotation
um den Ursprung um den Winkel 
:
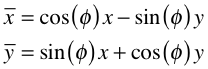
Reihenfolge
der Transformationen in der Regel nicht vertauschbar.