Hans Walser

Reuleaux-Zweiecke

Arbeitskreis SLA 1

Sa, 19. Nov. 2016, PH Zürich

Zusammenfassung: Analog zum Reuleaux-Dreieck, das sich in verschiedenen Positionen ins immer gleiche Quadrat einpassen lässt, gibt es Reuleaux-Zweiecke, die sich in ein gleichseitiges Dreieck einpassen lassen. Es werden zwei Beispiele vorgestellt sowie verschiedene Beweistechniken diskutiert: Rechnung, Einbinden in einen übergeordneten Zusammenhang, Kinematik. Ein wichtiger Aspekt ist die Beschreibung von Kurven in verschiedenen zueinander bewegten Referenzsystemen. Schließlich wird eine Verallgemeinerung auf Reuleaux-Vierecke besprochen.

1 Das Reuleaux-Dreieck

Das Reuleaux-Dreieck (Reuleaux, 1875, S. 131f) ist ein „Gleichdick“ (Schülerausdruck). Es hat in jeder Richtung den gleichen Durchmesser und lässt sich daher berührend in einen Streifen oder ein Quadrat einpassen.

Reuleaux-Dreieck im Streifen und im Quadrat

2 Ein Reuleaux-Zweieck

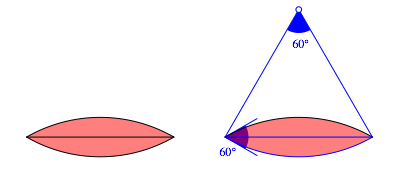
Reuleaux-Zweieck mit 60°-Winkel

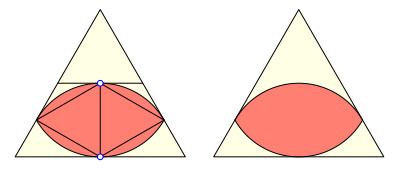
Wir können zwei der drei Bogen des Reuleaux-Dreiecks zu einem Reuleaux-Zweieck zusammenfügen. Dieses Zweieck wurde von Honsberger (1973, S. 56-58) beschrieben.

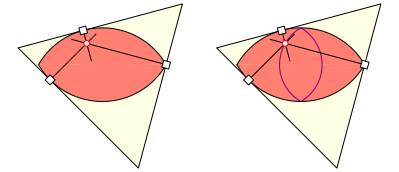
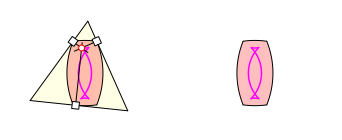
Die folgende Abbildung zeigt dieses Reuleaux-Zweieck im gleichseitigen Dreieck in zwei speziellen und einer allgemeinen Lage.

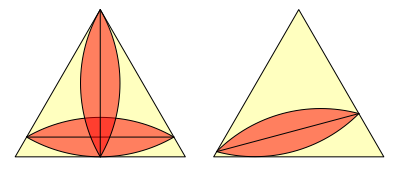
Reuleaux-Zweieck im Dreieck

Das Reuleaux-Zweieck ist kein Gleichdick.

Es hat zwei Winkel von 60° und kann daher die Ecken des Dreieckes gerade noch erreichen.

3 Beweis: Visuell und kinematisch

Wir beginnen mit dem Zweieck in der speziellen Lage mit horizontaler Sehne.

Startsituation und Verdrehung

Eine der fundamentalen Ideen in der Mathematik besteht darin, ein Problem in ein übergeordnetes einzubinden, worin die Lösung sofort sichtbar wird. Daher binden wir das Dreieck mit dem Zweieck in spezieller Lage in ein regelmäßiges Sechseck ein gemäß Abbildung. Jedes Zweieck liegt in „seinem“ Dreieck.

Nun drehen wir den Zweieck-Kranz um den Sechseckmittelpunkt um einen beliebigen Winkel. Jedes Zweieck ragt jetzt teilweise in das Nachbardreieck.

Wir passen blaue gleichseitige Stützdreiecke ein. Nun können wir jedes einzelne Zweieck parallel zur berührten Sechseckseite um die Seitenlänge der blauen Stützdreiecke zurückverschieben. Der Zweieck-Kranz wird aufgelöst.

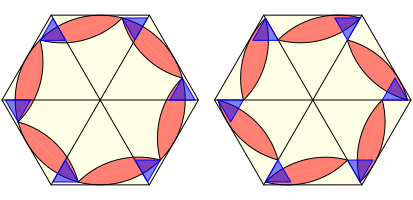
Stützdreiecke und Zurückschieben

Jedes Zweieck ist nun wieder in „seinem“ Dreieck, aber in allgemeiner Lage.

4 Das 120°-Zweieck

Die Abbildung zeigt das 120°-Zweieck (Reuleaux, 1875, S. 120f).

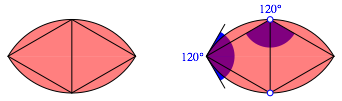
120°-Zweieck

Die folgenden Abbildungen zeigen die Einpassung ins gleichseitige Dreieck. Die Breite des Zweiecks und damit auch der Radius der Bögen ist die halbe Dreieckshöhe.

Horizontale Lage

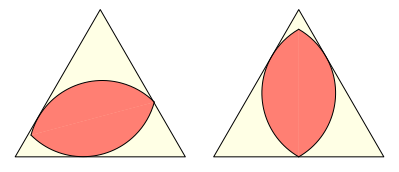
Schräge und senkrechte Lage

Wegen des 120°-Winkels sind die Dreiecksecken nicht erreichbar.

Die Einpass-Eigenschaft kann mit einem ähnlichen Beweis wie beim 60°-Zweieck gezeigt werden.

5 Ein Schnittpunkt

Drei Geraden verlaufen in der Regel nicht durch denselben Punkt. Wenn sie das trotzdem tun, ist das bemerkenswert. Klassische Beispiele im Schulunterricht sind die drei Schwerlinien, die drei Winkelhalbierenden, die drei Mittelsenkrechten der Seiten oder die drei Höhen eines beliebigen Dreiecks. Es gibt aber im Zusammenhang mit einem Dreieck noch viele andere Schnittunkte von drei Geraden, vgl. (Walser, 2012).

Wir nehmen nun eine allgemeine Lage des 120°-Zweiecks im Dreieck und zeichnen in den Berührpunkten die Normalen auf die Dreiecksseiten.

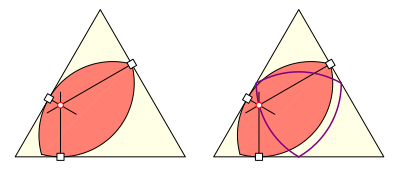
Schnittpunkt. Ort der Schnittpunkte relativ zum Dreieck

Wir stellen fest, dass die drei Normalen durch denselben Punkt verlaufen. Für den Nachweis der Schnittpunkteigenschaft benötigen wir eine kinematische Überlegung, vgl. (Honsberger, 1973, S. 62) und (Reuleaux, 1875, S. 119). Wenn sich eine Figur, welche eine andere berührt, berührend rotativ bewegen lässt, muss das momentane Drehzentrum auf der Berührungsnormalen liegen. Daher müssen in unserem Beispiel sämtliche drei Normalen durch denselben Punkt, eben das momentane Drehzentrum, verlaufen.

Das momentane Drehzentrum ist variabel, es bewegt sich sowohl relativ zum Dreieck wie auch relativ zum 120°-Zweieck.

Relativ zum Dreieck bewegt es sich auf einem Reuleaux-Dreieck.

Relativ zum 120°-Zweieck bewegt es sich auf einem 120°-Zweieck.

Ort der Schnittpunkte relativ zum Zweieck

6 Reuleaux-Zweiecke im gleichseitigen Dreieck

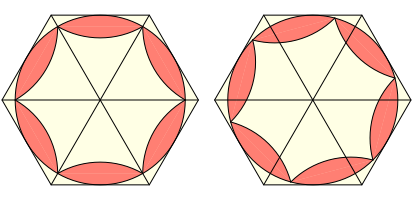
Im gleichseitigen Dreieck gibt es nur das 60°-Zweieck und das 120°-Zweieck so dass sie berührend gedreht werden können. Allenfalls kann man noch das 180°-Zweieck, den Inkreis also, dazu nehmen.

Reuleaux-Zweiecke im gleichseitigen Dreieck

7 Beliebiges Zweieck

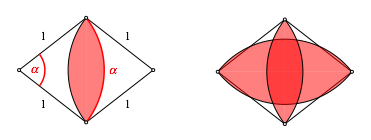
Wir beginnen mit einem beliebigen Rhombus der Seitenlänge 1 und einem Winkel .

Nun zeichnen wir zwei Zweiecke ein gemäß Abbildung. Der Winkel des Rhombus überträgt sich (im Bogenmaß) auf die Seitenlänge des Zweieckes.

Zwei Zweiecke

Die Schnittfigur der beiden Zweiecke ist ein Bogen-Viereck. Dieses Bogen-Viereck lässt sich ebenfalls auf verschiedene Arten in ein gleichseitiges Dreieck einpassen, so dass immer alle drei Dreiecksseiten berührt werden. Der Beweis läuft im Prinzip analog wie bei den Zweiecken.

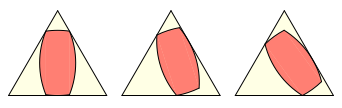
Einpassen ins Dreieck

Und ebenfalls schneiden sich die Berührungspunkt-Normalen in einem Punkt. Dies ist der momentane Drehpunkt.

Wird das Bogen-Viereck im gleichseitigen Dreieck verdreht, bewegt sich der Schnittpunkt relativ zum Dreieck auf einer Kurve, welche dieselben Symmetrien hat wie das gleichseitige Dreieck.

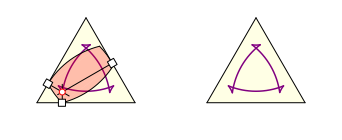
Bewegung relativ zum Dreieck

Wenn wir das Bogen-Viereck festhalten und das Dreieck darum herum bewegen, ergibt sich für den Schnittpunkt eine Kurve mit den Symmetrien des Bogen-Vierecks (Kleinsche Vierergruppe).