Hans Walser

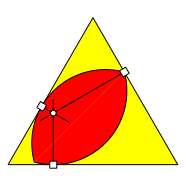
Reuleaux-Zweiecke

Arbeitskreis SLA 1

Sa, 19. Nov. 2016, PH Zürich

Zusammenfassung: Analog zum Reuleaux-Dreieck, das sich in verschiedenen Positionen ins immer gleiche Quadrat einpassen lässt, gibt es Reuleaux-Zweiecke, die sich in ein gleichseitiges Dreieck einpassen lassen. Es werden zwei Beispiele vorgestellt sowie verschiedene Beweistechniken gezeigt: Rechnung, Einbinden in einen übergeordneten Zusammenhang, Dualität, Kinematik. Ein wichtiger Aspekt ist die Beschreibung von Kurven in verschiedenen zueinander bewegten Referenzsystemen. Schließlich wird eine Verallgemeinerung auf Reuleaux-Vierecke besprochen. Dabei treffen wir auch im allgemeinen Fall auf invariante symmetrische Figuren.

1 Das Reuleaux-Dreieck

Das Reuleaux-Dreieck (Reuleaux, 1875, S. 131f) besteht aus drei Kreisbogen über den Seiten eines gleichseitigen Dreieckes. Die Zentren der Kreisbogen sind die jeweils dritte Ecke des Dreiecks. Das Reuleaux-Dreieck ist ein „Gleichdick“ (Schülerausdruck). Es hat in jeder Richtung den gleichen Durchmesser und lässt sich daher berührend in einen Streifen oder ein Quadrat einpassen.

Reuleaux-Dreieck im Streifen und im Quadrat

Das Reuleaux-Dreieck hat Winkel von 120°. Es kann daher die Quadratecken nicht erreichen.

Beschreibung: 010_1_Kunst.pdf

Bence Marafkó (H): Circle-Triangle in Circle 2, 2016, acrylic

2 Ein Reuleaux-Zweieck

Wir können zwei der drei Bogen des Reuleaux-Dreiecks zu einem Reuleaux-Zweieck zusammenfügen. Dieses Zweieck wurde von Honsberger (1973, S. 56-58) beschrieben.

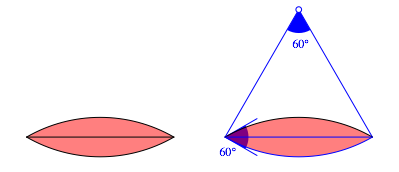
Reuleaux-Zweieck mit 60°-Winkel

Aus solchen Zweiecken lässt sich eine Figur mit Bifurkationen bauen so dass die Randlinien glatt ineinander übergehen. Die folgende Abbildung zeigt den „Goldenen Baum“ (Walser, 2013, S. 31).

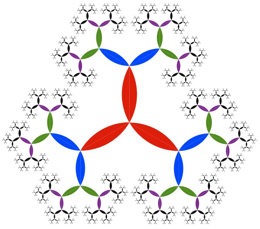
Goldener Baum

Die folgende Abbildung zeigt dieses Reuleaux-Zweieck im gleichseitigen Dreieck in zwei speziellen und einer allgemeinen Lage.

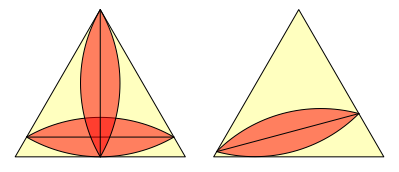
Reuleaux-Zweieck im Dreieck

Das Reuleaux-Zweieck ist kein Gleichdick. Es hat zwei Winkel von 60° und kann daher die Ecken des Dreieckes gerade noch erreichen. Die Sehnenlänge des Zweiecks ist die Höhe des Dreiecks.

3 Beweise für die Einpass-Eigenschaft

3.1 Auf Heller und Pfennig

Wir arbeiten in der Disposition der folgendenAbbildung.

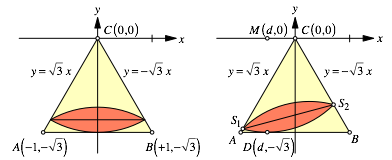
Abb. 3: Situation im Koordinatensystem

Das gleichseitige Dreieck ABC hat die Seitenlänge 2 und die Höhe . Diese Höhe ist auch der Bogenradius und die Sehnenlänge des Zweiecks. Der untere Bogen (Fischbauch) hat sein Zentrum im Ursprung C. Die Dreieckseiten AC und BC haben die Gleichungen beziehungsweise .

In der schrägen Situation sei nun der Berührungspunkt des unteren Bogens mit der Basislinie AB des Dreiecks. Der Trägerkreis dieses unteren Bogens hat daher den Mittelpunkt und die Gleichung . Der Schnitt mit den Dreiecksseiten AC und BC liefert die Schnittpunkte:

(1)

und

(2)

Daraus ergibt sich der Abstand . Wir können also genau unser Zweieck einpassen.

3.2 Visuell und kinematisch

Wir beginnen mit dem Zweieck in der speziellen Lage mit horizontaler Sehne.

Eine der fundamentalen Ideen in der Mathematik besteht darin, ein Problem in ein übergeordnetes einzubinden, worin die Lösung sofort sichtbar wird. Daher binden wir das Dreieck mit dem Zweieck in spezieller Lage in ein regelmäßiges Sechseck ein gemäß Abbildung. Jedes Zweieck liegt in „seinem“ Dreieck.

Nun drehen wir den Zweieck-Kranz um den Sechseckmittelpunkt um einen beliebigen Winkel (Abbildung für den Drehwinkel 15°). Jedes Zweieck ragt jetzt teilweise in das Nachbardreieck.

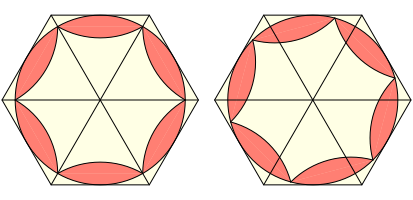
Startsituation und Verdrehung

Wir passen blaue gleichseitige Stützdreiecke ein. Nun können wir jedes einzelne Zweieck parallel zur berührten Sechseckseite um die Seitenlänge der blauen Stützdreiecke zurückverschieben. Der Zweieck-Kranz wird aufgelöst.

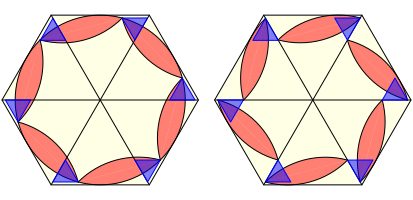
Stützdreiecke und Zurückschieben

Jedes Zweieck ist nun wieder in „seinem“ Dreieck, aber in allgemeiner Lage.

4 Das 120°-Zweieck

Die Abbildung zeigt das 120°-Zweieck (Reuleaux, 1875, S. 120f).

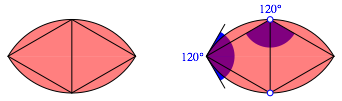
120°-Zweieck

Die folgenden Abbildungen zeigen die Einpassung ins gleichseitige Dreieck. Die Breite des Zweiecks und damit auch der Radius der Bögen ist die halbe Dreieckshöhe.

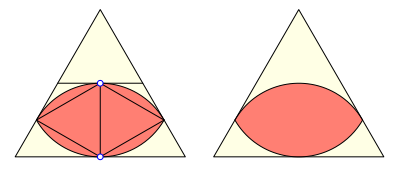
Horizontale Lage

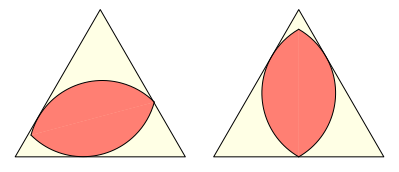
Schräge und senkrechte Lage

Wegen des 120°-Winkels sind die Dreiecksecken nicht erreichbar.

5 Beweis der Einpass-Eigenschaft

Wir arbeiten wieder im Sixpack. Die blauen Punkte sind die Zentren der Außenbögen der Zweiecke. Wir drehen nun jedes Zweieck um je diesen blauen Punkt um je denselben Winkel. Dabei schleift je eine Spitze des einen Zweiecks auf dem Innenbogen des nachfolgenden Zweiecks.

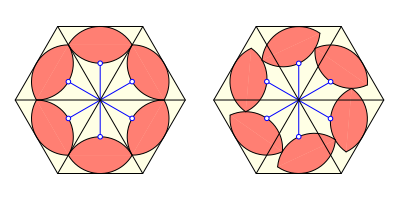
Sixpack

Dies wird einsichtig durch den in der folgenden Figur eingezeichneten Rhombus, den man sich als Gelenkmodell vorstellen muss. Die nicht eingezeichnete Rhomben-Kante steht dabei senkrecht zur Trennlinie der beiden Hintergrunddreiecke. Die Tangente an das rechte Zweieck im Berührungspunkt der beiden Zweiecke ist daher parallel zu dieser Trennlinie.

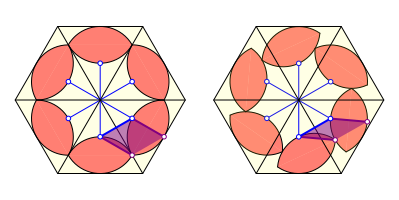
Beweglicher Rhombus

Die folgende Abbildung zeigt ein mechanisches Modell in Vorderansicht (Rhombus im Vordergrund) und Rückansicht.

Mechanisches Modell

Wir können nun wiederum kleine gleichseitige Dreiecke einzeichnen und dann die Zweiecke zurückschieben.

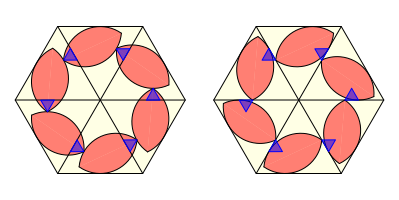
Zurückschieben

6 Dualität

Wir zeichnen in das 120°-Zweieck zusätzlich ein 60°-Zweieck ein. Die Eckpunkte des einen Zweiecks sind nun die Zentren der Bögen des anderen Zweiecks und umgekehrt.

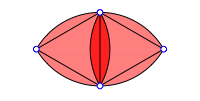
Duale Zweiecke

In der Figur erkennen wir zusätzlich zwei Reuleaux-Dreiecke. Die Vereinigung (im Sinne der Mengensprache) der beiden Reuleaux-Dreiecke ist das 120°-Zweieck, der Durchschnitt das 60°-Zweieck.

Wir passen nun die Figur ins Dreieck ein. Dabei stellen wir fest, dass das 60°-Zweieck offenbar ins Seitenmittendreieck des großen Dreiecks eingepasst ist. Um dies einzusehen, denken wir uns drei Streifen je zwischen einer Seite des großen Dreiecks und der dazu parallelen Seite des Seitenmittendreiecks. In jedem dieser Streifen funktioniert ein Reuleaux-Dreieck.

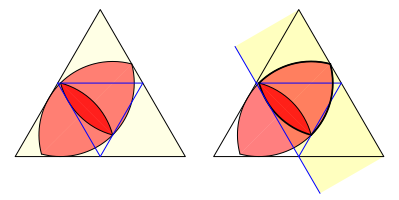
Dreieck und duales Dreieck

Aus der Einpass-Eigenschaft des 120°-Zweiecks folgt daher die Einpass-Eigenschaft des dualen 60°-Zweiecks und umgekehrt.

7 Ein Schnittpunkt

Drei Geraden verlaufen in der Regel nicht durch denselben Punkt. Wenn sie das trotzdem tun, ist das bemerkenswert. Klassische Beispiele im Schulunterricht sind die drei Schwerlinien, die drei Winkelhalbierenden, die drei Mittelsenkrechten der Seiten oder die drei Höhen eines beliebigen Dreiecks. Es gibt aber im Zusammenhang mit einem Dreieck noch viele andere Schnittunkte von drei Geraden, vgl. (Walser, 2012).

Wir nehmen nun eine allgemeine Lage des 120°-Zweiecks im Dreieck und zeichnen in den Berührpunkten die Normalen auf die Dreiecksseiten.

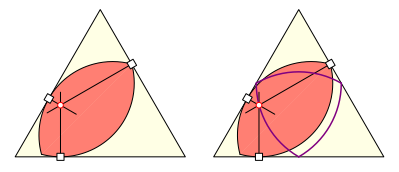
Schnittpunkt. Ort der Schnittpunkte relativ zum Dreieck

Wir stellen fest, dass die drei Normalen durch denselben Punkt verlaufen. Für den Nachweis der Schnittpunkteigenschaft benötigen wir eine kinematische Überlegung, vgl. (Honsberger, 1973, S. 62) und (Reuleaux, 1875, S. 119). Wenn sich eine Figur, welche eine andere berührt, berührend rotativ bewegen lässt, muss das momentane Drehzentrum auf der Berührungsnormalen liegen. Daher müssen in unserem Beispiel sämtliche drei Normalen durch denselben Punkt, eben das momentane Drehzentrum, verlaufen.

Das momentane Drehzentrum ist variabel, es bewegt sich sowohl relativ zum Dreieck wie auch relativ zum 120°-Zweieck.

Relativ zum Dreieck bewegt es sich auf einem Reuleaux-Dreieck.

Relativ zum 120°-Zweieck bewegt es sich auf einem 120°-Zweieck.

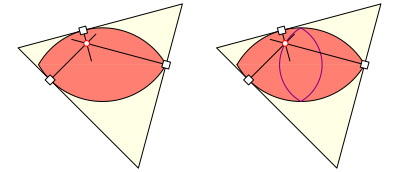
Ort der Schnittpunkte relativ zum Zweieck

8 Reuleaux-Zweiecke im gleichseitigen Dreieck

Im gleichseitigen Dreieck gibt es nur das 60°-Zweieck und das 120°-Zweieck so dass sie berührend gedreht werden können. Allenfalls kann man noch das 180°-Zweieck, den Inkreis also, dazu nehmen.

Reuleaux-Zweiecke im gleichseitigen Dreieck

Für den Ausschluss weiterer Bogen-Zweiecke verfahren wir wie folgt.

8.1 Disposition

Das Bogen-Zweieck habe den Bogenradius 1 und den Zentriwinkel für jeden der beiden Bögen. Es gelten dann die in der Abbildung eingetragenen Beziehungen.

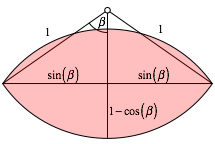
Das Zweieck

An den beiden Ecken hat das Bogen-Zweieck dann die Innenwinkel . (Der Innenwinkel ergibt sich durch die Tangenten an die Kreisbögen in der Ecke des Zweiecks.)

8.2 Fallunterscheidung

Wir unterscheiden folgende drei Fälle bezüglich des Winkels :

1. („Zahnstocher“)

2. („mittleres Zweieck“)

3. („dicke Zweiecke“)

Die Fallunterscheidungen sind nicht disjunkt, sondern haben gemeinsame Grenzen.

In jedem der drei Fälle zeichnen wir das Bogen-Zweieck im Querformat und im Hochformat und umschreiben ein gleichseitiges Dreieck. Falls das zur Diskussion stehende Bogen-Zweieck sich in einem gleichseitigen Dreieck berührend drehen lässt, müssen die beiden umbeschriebenen Dreiecke dieselbe Höhe haben. Damit haben wir eine notwendige Bedingung für die zulässigen Winkel .

8.2.1 Zahnstocher

Es ist also . Die Abbildung 2 zeigt das Beispiel für .

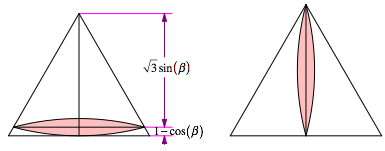
Abb. 2: Zahnstocher. beta = 15°

Für den Zahnstocher im Querformat erhalten wir die Dreieckshöhe:

(3)

Für den Zahnstocher im Hochformat erhalten wir die Dreieckhöhe:

(4)

Die Bedingung liefert die Gleichung:

(5)

Die Gleichung (5) hat im Intervall die Lösung:

(6)

Das ist die Rand-Lösung.

8.2.2 Mittleres Zweieck

Es ist: . Die Abbildung 3 zeigt das Beispiel für .

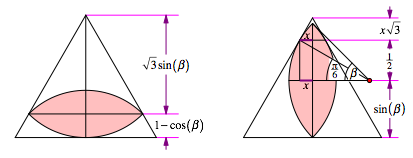
Abb. 3: beta = 45°

Beim Bogen-Zweieck im Querformat ergibt sich die Dreieckshöhe wie bei (3):

(7)

Für das Hochformat berechnen wir zunächst die Hilfsgröße x:

(8)

Damit erhalten wir die Dreieckshöhe:

(9)

Gleichsetzen der beiden Höhen liefert:

(10)

Die Gleichung (10) hat im Intervall die beiden Lösungen:

und (11)

Das sind die beiden Rand-Lösungen.

8.2.3 Dickes Zweieck

Es ist . Die Abbildung 4 zeigt das Beispiel für .

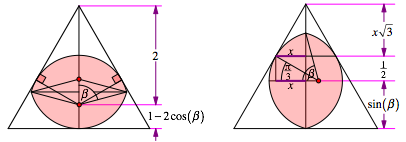
Abb. 4: Dickes Zweieck. beta = 75°

Beim Querformat erhalten wir die Dreieckshöhe:

(12)

Für das Hochformat benötigen wir wiederum die Hilfsgröße (8) und erhalten die Dreieckshöhe wie bei (9):

(13)

Gleichsetzen liefert:

(14)

Die Gleichung (14) hat im Intervall die beiden Rand-Lösungen:

und (15)

Somit haben wir als einzige Lösungen die Bogen-Zweiecke mit Innenwinkeln von 60°, 120° und 180°. Letzteres ist der Inkreis des Dreiecks.

9 Selbstkontrolle

Die beiden Bögen des Selbstkontrolle-Signets haben unterschiedliche Krümmungen. Der obere Bogen ist stärker gekrümmt.

Selbstkontrolle

10 Calissons de Provence

Französisches Konfekt aus Aix-en-Provence.

Calissons de Provence

Die Form der Calissons ist ein Bogen-Zweieck mit einem nicht speziellen Winkel.

„Allgemeines“ Zweieck

11 Dualität im allgemeinen Fall

11.1 Duale Zweiecke

Wir beginnen mit einem beliebigen Rhombus der Seitenlänge 1 und einem Winkel .

Nun zeichnen wir zwei duale Zweiecke ein gemäß Abbildung. Der Winkel des Rhombus überträgt sich (im Bogenmaß) auf die Seitenlänge des Zweieckes.

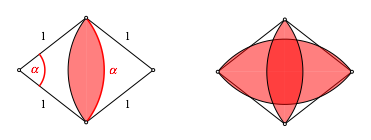
Duale Zweiecke

Diese Figur hat einige bemerkenswerte Eigenschaften.

11.2 Gleichseitige Dreiecke

In die Situation der vier Rhomben-Ecken und der vier Schnittpunkte der beiden Zweiecke lassen sich gleichseitige Dreiecke einzeichnen.

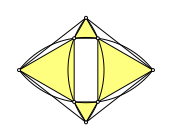
Gleichseitige Dreiecke

Der Beweis ergibt sich aus folgendem. Zunächst haben wir ein offensichtlich gleichseitiges Dreieck (zyan), das wir in einen Sektorbogen umwandeln.

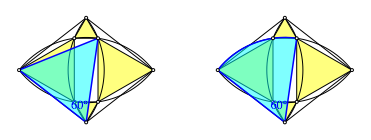
Dreieck und Sektor

Den Bogen können wir als Ortsbogen für einen Winkel von 150° interpretieren. Dann ist alles klar.

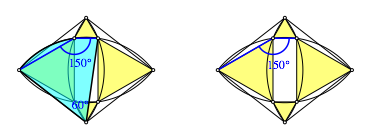
Ortsbogen

11.3 Bogen-Viereck

Die Schnittfigur der beiden dualen Zweiecke ist ein Bogen-Viereck.

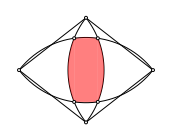
Bogen-Viereck

Es zeigt sich, dass dieses Bogenviereck eine von der Form des Ausgangsrhombus unabhängigen Umfang hat. Zur Berechnung der Seitenbogen-Längen ergänzen wir die Figur mit zwei Dreiecken (zyan). Diese Dreiecke sind gleichseitig. Der große blaue Bogen hat daher die Länge . Da der rote Bogen die Länge hat, bleibt für den kurzen Bogen die Länge .

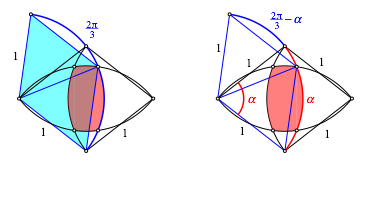
Ergänzung der Figur mit gleichseitigen Dreiecken

Dies ist aber auch die Länge eines langen Seitenbogens des Bogen-Viereckes.

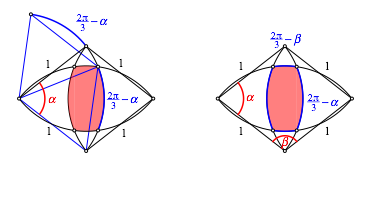
Bogenlänge im Bogen-Viereck

Entsprechend hat ein kurzer Seitenbogen des Bogen-Viereckes die Länge .

Für den Umfang des Bogen-Viereckes finden wir:

(16)

Wegen (Winkel im Rhombus) erhalten wir den Umfang . Dies ist ein Drittel des Umfanges des Einheitskreises.

11.4 Einpassen ins Dreieck

Das Bogen-Viereck lässt sich ebenfalls auf verschiedene Arten in ein gleichseitiges Dreieck einpassen, so dass immer alle drei Dreiecksseiten berührt werden. Der Beweis läuft im Prinzip analog wie bei den Zweiecken.

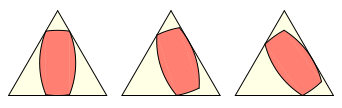
Einpassen ins Dreieck

11.5 Schnittpunkt

Und ebenfalls schneiden sich die Berührungspunkt-Normalen in einem Punkt. Dies ist der momentane Drehpunkt.

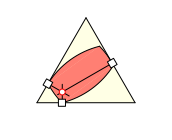
Schnittpunkt

Wird das Bogen-Viereck im gleichseitigen Dreieck verdreht, bewegt sich der Schnittpunkt relativ zum Dreieck auf einer Kurve, welche dieselben Symmetrien hat wie das gleichseitige Dreieck.

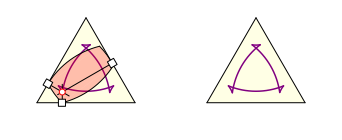
Bewegung relativ zum Dreieck

Wenn wir das Bogen-Viereck festhalten und das Dreieck darum herum bewegen, ergibt sich für den Schnittpunkt eine Kurve mit den Symmetrien des Bogen-Vierecks (Kleinsche Vierergruppe).

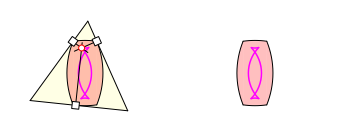
Relativ zum Bogen-Viereck

Dank

Der Autor dankt Renato Pandi für viele Ideen und Anregungen.

Literatur

Honsberger, Ross (1973): Mathematical Gems. From Elementary Combinatorics, Number Theory, and Geometry. The Mathematical Association of America.

Reuleaux, Franz (1875): Lehrbuch der Kinematik. Erster Band: Theoretische Kinematik. Braunschweig: Vieweg.
e-Version: https://ia700409.us.archive.org/29/items/lehrbuchderkine01reulgoog/lehrbuchderkine01reulgoog.pdf

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Websites

Abgerufen 2. Mai 2016

Delta-Bogenvielecke

www.walser-h-m.ch/hans/Miniaturen/D/Delta-Bogenvielecke/Delta-Bogenvielecke.htm

Delta-Kurven-Umfang

www.walser-h-m.ch/hans/Miniaturen/D/Delta-Kurven-Umfang/Delta-Kurven-Umfang.htm

Gleichdick

www.walser-h-m.ch/hans/Miniaturen/G/Gleichdick/Gleichdick.htm

Gleichdick mit Kartoffeln

www.walser-h-m.ch/hans/Miniaturen/G/Gleichdick_Kartoffeln/Gleichdick_Kartoffeln.htm

Gleichdick mit Zykloiden

www.walser-h-m.ch/hans/Miniaturen/G/Gleichdick_Zykloide/Gleichdick_Zykloide.htm