SEMI-REGULAR FIGURES.
BETWEEN BEAUTY AND REGULARITY
Hans
Walser, Basel University, Switzerland
hwalser@bluewin.ch
Abstract: Cutting away a rhombus from a regular
pentagon, the leftover will be a semi-regular pentagon. Using this semi-regular
pentagon as tile, we can build various ornaments, tilings, crystallographic
patterns, and spirals. We will find also a semi-regular not convex
dodecahedron. The regular and the semi-regular dodecahedron together can fill
the space without gaps or overlapping.
The semi-regular pentagon
The regular pentagon is a bad guy.
We canŐt use it for a tiling of the plane. There
occurs a gap of 36ˇ (Fig. 1c) (Grźnbaum and Shephard 1987, Frontispiece).
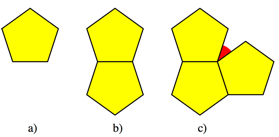
Fig. 1: No tiling with regular pentagons
Now we modify the regular pentagon (Fig. 2a). We flip
down a vertex (Fig. 2b). The remaining part will be our semi-regular pentagon
(Fig. 2c). The semi-regular pentagon has equal sides, but not equal angles.
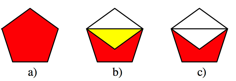
Fig. 2: The semi-regular pentagon
Though our semi-regular pentagon has some defects
compared to the regular pentagon, it has also some advantages.
Combination with the regular pentagon
We find a tiling with a combination of regular and
semi-regular pentagons (Fig. 3a).
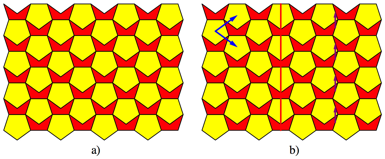
Fig. 3: Tiling with pentagons and semi-regular pentagons
The tiling contains translational symmetries,
indicated by blue arrows in the figure 3b, axial symmetries (red) and glide-reflection
symmetries (purple).
The figure 4 depicts an example with a fivefold
rotational symmetry.
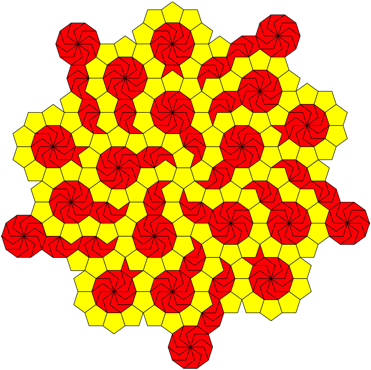
Fig. 4: Fivefold rotational symmetry
Frieze patterns and tilings
Nevertheless we may build frieze patterns and tilings
just out of our semi-regular pentagon.
The figure 5 depicts a frieze pattern. With respect to
the colors it has translational symmetry only. Without respect to the colors we
have additionally a glide-reflection symmetry.
![]()
Fig. 5: Frieze pattern
The tiling of the figure 6a is just an overlapping of
the frieze pattern of the figure 5. In this figure we may get the victim of an
optical illusion. Are the horizontal lines parallel?
The figure 6b depicts a more elegant tiling.
WhatŐs the difference between the figures 6c and 6d?![]()
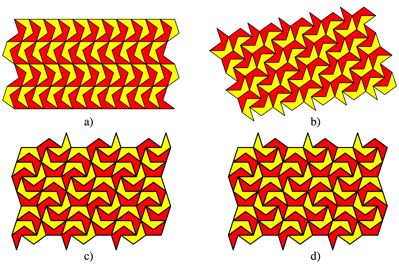
Fig. 6: Tilings
Rings and spirals
The figure 7a gives a constellation with concentric
rings. The figure 7b is basically the same, but the colors are exchanged such
that there are always two different colors at an edge.

Fig. 7: Concentric rings
First we see nothing special in the figure 8a. But a
closer look reveals a spiral (Fig. 8b). The width of the spiral is constant, so
we have an Archimedean spiral.

Fig. 8: Spirals
The figure 9 depicts two and ten Archimedean spirals
respectively.

Fig. 9: More spirals
In the three-dimensional space
With twelve regular pentagons as faces we can build
the regular dodecahedron (Fig. 10a). Together with the regular tetrahedron, the
cube, the octahedron, and the icosahedron it belongs to the five regular
Platonic solids.
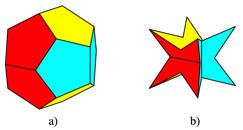
Fig. 10: Regular and semi-regular dodecahedron
With twelve semi-regular pentagons we can build the
semi-regular dodecahedron (Fig. 10b).
Relation to the cube
The semi-regular dodecahedron fits obviously in a cube
(Fig. 11b). But we can also draw a cube on the faces of the regular
dodecahedron (Fig. 11a).
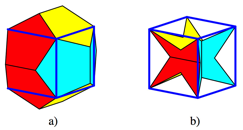
Fig. 11: Relation to the cube
The regular dodecahedron may be seen as a compound of
a cube with a hip roof on every face. And surprisingly the semi-regular
dodecahedron is just the leftover when we cut away a hip roof at every side of
the cube. So we have related construction principles. The regular dodecahedron
is positive, the semi-regular dodecahedron negative. The hip roof excess of the
regular dodecahedron corresponds to the hip roof deficit of the semi-regular
dodecahedron.
The figure 12 depicts the situation between the two
dodecahedra.
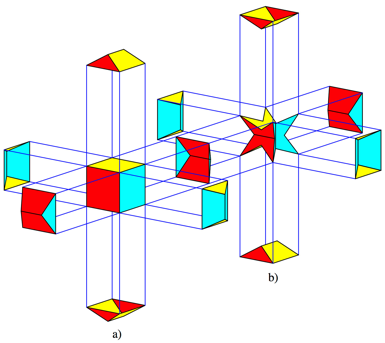
Fig. 12: Hip roofs
The hip roof cut away from the cube at the right (Fig.
12b) goes to the cube at the left (Fig. 12a). We have a situation similar to
the situation of anions and cations in chemistry.
A singular hip roof has the dimensions indicated in
the figure 13.
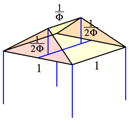
Fig. 13: Dimensions of the hip roof
The notation ![]() means the
Golden Section (Walser 2001 and 2013)
means the
Golden Section (Walser 2001 and 2013) ![]() . The height of the roof is
. The height of the roof is ![]() .
.
Eight-pointes stars
The semi-regular dodecahedron is an eight-pointed star
(Fig. 14b). But it is different from the similar looking Kepler star or stella octangula (Fig.
14a).
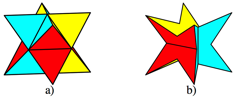
Fig. 14: Kepler star and semi-regular dodecahedron
Symmetry groups and topology
The symmetry groups of the regular and the
semi-regular dodecahedra are different. The semi-regular dodecahedron has just
the symmetry group S4 of the regular tetrahedron.
The regular and the semi-regular dodecahedra have the
same topology (Fig. 15 and 16). Both have 20 vertices, but in the semi-regular
case 12 of the vertices are hyperbolic.
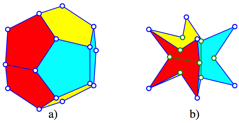
Fig. 15: Vertices, edges, and faces
Both have 30 edges, but in the semi-regular case six
of the vertices are like the bottom of a valley.
The regular dodecahedron
has 12 regular pentagons as faces, in the case of the semi-regular dodecahedron
the 12 faces are semi-regular pentagons.
In the diagrams of the figure 16 we see how the
vertices and edges are connected. There is no difference between the two
dodecahedra.
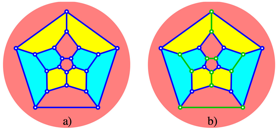
Fig. 16: Diagrams for regular and semi-regular dodecahedron
Model
We can build a paper model of the semi-regular
dodecahedron (Fig. 17a).
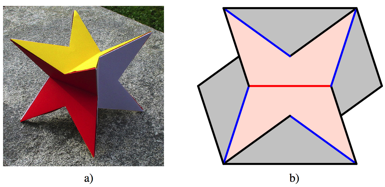
Fig. 17: Paper model
We need 6 parts according to figure 17b. We have to
cut along the black lines, fold in the sense of a valley fold along the red
line and in the sense of a mountain fold along the blue lines.
The red area remains visible on the outside, and the
gray areas can be tucked in or glued. Hint: The model will not be very stable.
Therefore I built first a model with reduced size (98%) and the visible model
as second layer on it.
Filling the space
Because of the relative situation between the two
dodecahedra (Fig. 12) the regular dodecahedron can sit on the semi-regular
dodecahedron like the egg on an eggcup (Fig. 18).
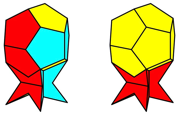
Fig. 18: Eggcup
Neither the regular nor the semi-regular dodecahedra
are space fillers (Coxeter 1973, p. 68f). But we can fill the space with
regular dodecahedra combined with semi-regular dodecahedra (Fig. 19).
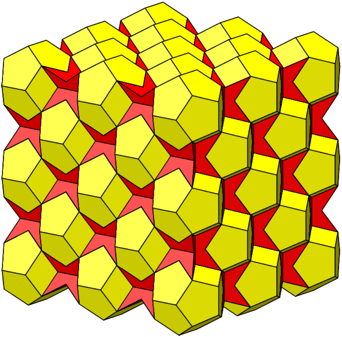
Fig. 19: Filling the space
The figure 19 is somehow the spatial analogue to the
figure 3.
The proof of the space-filling property is easy. First, the cube is a space filler. So we fill the space with cubes and color the cubes in black and white like a three-dimensional chessboard. Now we cut away the hip roofs from the black cubes and add them to the adjacent white cubes.
References
Coxeter, H. S. M. (1973): Regular Polytopes. Third Edition. New York: Dover 1973. ISBN 0-486-61480-8.
Grźnbaum, B. and Shephard, G. C. (1987): Tilings and Patterns. New York: Freeman. ISBN 0-7167-1193-1.
Walser, H. (2001): The Golden Section. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America 2001. ISBN 0-88385-534-8.
Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.