Hans Walser

 

 

Symmetrie als Werkzeug

 

Arbeitskreis Geometrie der GDM

 

8. - 10. September 2017

SaarbrŸcken

 

Zusammenfassung: Die Klassifikation der Symmetriegruppen der FlŠchenornamente wird als Hilfsmittel fŸr den Beweis eines Theorems aus der Elementargeometrie verwendet. Die Idee dabei ist, ein lokales PhŠnomen in eine †bersichtsdarstellung einzubinden und von daher zu verstehen.

1     Das Theorem

Wir setzen den Seiten eines Sehnenvierecks Parallelogramme an (Abb. 1a). Die Parallelogramme sind jeweils aus zwei gegenŸberliegenden Seiten des Sehnenviereckes gebildet und haben alle denselben, aber beliebigen spitzen Winkel (kann auch ein rechter Winkel sein). Die spitzen Winkel der Parallelogramme sind zyklisch angeordnet. Die zyklische Anordnung der Parallelogramme ist daher ãwindrŠdchenartigÒ. GegenŸberliegende Parallelogramme sind kongruent, aber ungleichsinnig orientiert.

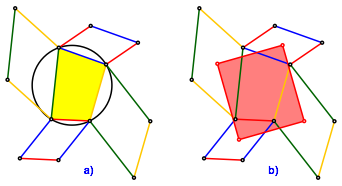
Abb. 1: Sehnenviereck und Parallelogramme

Theorem (E. V., M.): Die Mittelpunkte der Parallelogramme sind die Ecken eines Rechteckes (Abb. 1b).

2     Erwachende Wissenschaft

2.1    Allgemein

Die Entstehung von Wissenschaft und Bildung erfolgt oft nach dem Muster:

á            Sammeln

á            Ordnen – Ordnungskriterien

á            Struktur

á            Theorie

2.2    FlŠchenornamente

Im Bereich der FlŠchenornamente kann das etwas so aussehen:

á            Sammeln schšner Bildchen, etwa aus der Alhambra oder dem Taj Mahal

á            Ordnen nach Symmetriekriterien

á            Struktur im Sinne einer Klassifikation. Im Anhang ist eine Klassifizierungshilfe als Flussdiagramm angegeben

á            Theorie. Es gibt genau 17 Symmetrieklassen (Niggli 1924), (P—lya 1924)

Im Unterschied zu analogen Klassifikationen in den Naturwissenschaften kann in der Mathematik bewiesen werden, dass es eine weiteren Beispiele mehr gibt. Damit kann die Klassifikation als Werkzeug verwendet werden: jedes neu auftauchende FlŠchenornament muss zu einer der 17 Symmetrieklassen gehšren. Die Eigenschaften in der betreffenden Symmetrieklasse gelten dann fŸr das neu aufgetauchte FlŠchenornament.

2.3    Exkurs: Kristallografische Restriktion

Der SchlŸssel zur abschlie§enden Auflistung der 17 Symmetrieklassen ist die sogenannte kristallografische Restriktion.

In einem FlŠchenornament kšnnen nur folgende Drehwinkel erscheinen:

   180¡ (Halbdrehungen, Punktspiegelungen)

   120¡ (Dritteldrehungen)

     90¡ (Vierteldrehungen)

     60¡ (Sechsteldrehungen)

Insbesondere kšnnen keine Drehungen um 72¡ (FŸnfteldrehungen) erscheinen. Wir kšnnen die Ebene nicht mit regelmŠ§igen FŸnfecken parkettieren.

Abb. 2: Der muss drau§en bleiben

Als Folge der kristallografischen Restriktion kommen auch nur wenige Winkel als Schnittwinkel von Symmetrieachsen und/oder Schubspiegelachsen in Frage. Diese Winkel sind 0¡ (parallel), 90¡ (orthogonal), 60¡, 45¡ und 30¡.

2.4    Beschreibung der 17 Symmetrieklassen

Die Tabelle 1 gibt eine Beschreibung zu jeder Symmetrieklasse. Die Bezeichnung erfolgt gemŠ§ IUC (International Union of Crystallography).

 

p1

Nur Translationssymmetrie. Parallelogrammgitter

cm

Abwechselnd parallele Spiegelachsen und Schubspiegelachsen.

Keine Rotationssymmetrie. Rhombengitter

pm

Zwei Klassen zueinander paralleler Spiegelachsen.

Keine Rotationssymmetrie. Rechteckgitter 

pg

Zwei Klassen zueinander paralleler Schubspiegelachsen.

Keine Rotationssymmetrie. Rechteckgitter 

p2

Vier Klassen von zweizŠhligen Drehzentren. Parallelogrammgitter

cmm

Zwei Klassen orthogonaler Spiegelachsen mit zweizŠhligen Drehzentren an den Schnittpunkten. Zwei Klassen orthogonaler Schubspiegelachsen mit zweizŠhligen Drehzentren an den Schnittpunkten. Rhombengitter

pmm

Symmetrien des Rechteckgitters: Symmetrieachsen (Gitterlinien und Mittellinien). ZweizŠhlige Drehzentren (Rechteckmitten, Kantenmitten, Ecken).

pmg

Parallele Spiegelachsen. Orthogonal dazu zwei Klassen von Schubspiegelachsen mit zweizŠhligen Drehzentren in den Schnittpunkten. Rechteckgitter

pgg

Keine Symmetrieachsen. Orthogonale Schubspiegelachsen. Dazwischen zweizŠhlige Drehzentren. Rechteckgitter

p4

Keine Spiegelachsen. VierzŠhliger Drehzentren. Dazwischen zweizŠhlige Drehzentren. Quadratgitter

p4m

Symmetrien des Quadratgitters: Symmetrieachsen (Kanten, Mittellinien, Diagonalen). Schubspiegelachsen zwischen den Diagonalen. VierzŠhlige Drehzentren (Ecken und Quadratmitten). ZweizŠhlige Drehzentren (Kantenmitten)

p4g

Zwei Klassen von vierzŠhligen Drehzentren. Dazwischen zweizŠhlige Drehzentren. Zwei Klassen von orthogonalen Symmetrieachsen. Dazwischen zwei Klassen von orthogonalen Schubspiegelachsen. Quadratgitter

p3

Drei Klassen von dreizŠhligen Drehzentren. Hexagonalgitter

p3m1

Zwei Klassen von dreizŠhligen Drehzentren. Drei Klassen von Symmetrieachsen, Schnittpunkte in den Drehzentren. Hexagonalgitter

p31m

Drei Klassen von dreizŠhligen Drehzentren. Drei Klassen von Symmetrieachsen, Schnittpunkte in den Drehzentren einer Klasse. Dazwischen Schubspiegelachsen. Drehzentren der beiden anderen Klassen nicht auf Symmetrieachsen. Hexagonalgitter

p6

SechszŠhlige, dreizŠhlige und zweizŠhlige Drehzentren. Keine Symmetrieachsen. Keine Schubspiegelachsen. Hexagonalgitter

p6m

Symmetrien des Hexagonalgitters: SechszŠhlige Drehzentren (Sechseckzentren), dreizŠhlige Drehzentren (Ecken), zweizŠhlige Drehzentren (Kantenmitten). Symmetrieachsen durch Sechseckzentren, schneiden sich unter 30¡. Schubspiegelachsen durch Kantenmitten

Tab. 1: Beschreibung der Symmetrieklassen

2.5    Unterricht

FŸr Bandornamente gibt es analoge kristallografische EinschrŠnkung und nur sieben Symmetrieklassen.

Dies lŠsst sich im Unterricht bearbeiten. Der Autor hat das auf Sekundarstufe 1 und Sekundarstufe 2 sowie der Lehramtsausbildung fŸr diese Stufen getan. Es gibt SchŸlerinnen und SchŸler, die den Einstieg Ÿber das Sammeln und Ordnen wŠhlen und andere, welche mit Kombinationen der in einem Bandornament mšglichen Symmetrien arbeiten.

3     Beweis des Theorems

Wir haben zu zeigen, dass die Mittelpunkte der Parallelogramme der Abbildung 1b ein Rechteck bilden. Die Parallelogramme, die alle dieselben Winkel haben, ergaben sich durch Ansetzen an die Seiten eines Sehnenviereckes gemŠ§ Abbildung 1a.

Im Sehnenviereck ergŠnzen sich gegenŸberliegende Winkel auf 180¡ (Abb. 3a).

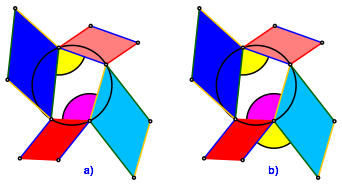
Abb. 3: ErgŠnzungswinkel und gleiche Winkel

In den Parallelogrammen ergŠnzen sich spitze und stumpfe Winkel ebenfalls auf 180¡. Daraus ergibt sich, dass die beiden in der Abbildung 3b gelb eingezeichneten Winkel gleich gro§ sind.

Ein Vergleich der Schenkel dieser beiden Winkel zeigt aber, dass sie zwar betragsmŠ§ig gleich gro§ sind, aber unterschiedlich orientiert (Abb. 4a).

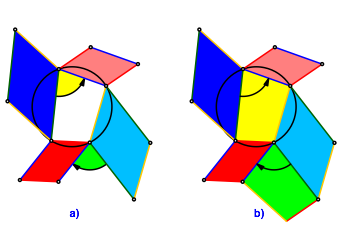
Abb. 4: Entgegengesetze Orientierung

Daher kšnnen wir in die LŸcke des Au§enwinkels ein zum ursprŸnglichen Sehnenviereck gegenglich orientiertes kongruentes Sehnenviereck einpassen (grŸn in Abb. 4b). Entsprechend kšnnen wir auch an den Ÿbrigen Au§enwinkeln grŸne Sehnenvierecke eingepasst werden (Abb. 5a).

Nun kšnnen wir mit den grŸnen Sehnenvierecken verfahren wie ursprŸnglich mit dem gelben: wir setzen Parallelogramme an und passen in die Au§enwinkel nun gelbe Sehnenvierecke ein (Abb. 5b). So entsteht ein FlŠchenornament.

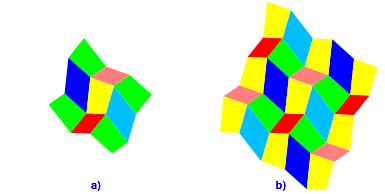
Abb. 5: ErgŠnzung zum Parkett

Die Abbildung 6 zeigt die WeiterfŸhrung des FlŠchenornamentes.

Abb. 6: FlŠchenornament

4     Symmetrien

Welche Symmetrien hat das FlŠchenornament der Abbildungen 5 und 6?

Wir erkennen sofort Symmetriezentren (Abb. 7a). Das sind die Mittelpunkte der Parallelogramme. Wir sehen, dass diese Symmetriezentren ein Rechteckraster bilden – aber das ist ja genau das, was wir fŸr unser Theorem noch beweisen mŸssen.

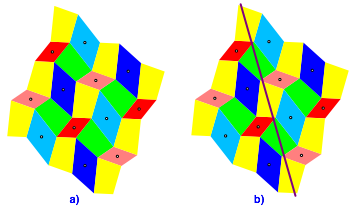
Abb. 7: Symmetriezentren und eine Schubspiegelachse

Nach einigem Suchen entdecken wir als weitere Symmetrien Schubspiegelsymmetrien. In der Abbildung 7b ist exemplarisch eine Schubspiegelachse eingezeichnet. Wir kšnnen etwa ein dunkelblaues Parallelogramm schieben und dann Spiegeln, so dass es mit einem hellblauen Parallelogramm zur Deckung kommt.

5     Exkurs: Schubspiegelung

Schubspiegelsymmetrie wird im Unterricht kaum behandelt, obwohl sie im Alltag die hŠufigste (!) Symmetrie ist. Daher lohnt sich ein eigener Abschnitt dazu.

5.1    Der aufrechte Gang

Die Fu§spur eines Menschen in Sand oder im Schnee hat eine Schubspiegelsymmetrie (Abb. 8). Wir legen also tŠglich mehrere Kilometer Schubspiegelsymmetrie hin.

Abb. 8: Schubspiegelsymmetrie

Problem 1: Gibt es weitere Lebewesen, deren Fu§spur Schubspiegelsymmetrie hat?

Problem 2: Hat die Fu§spur eines hinkenden Menschen (Abb. 9) ebenfalls Schubspiegelsymmetrie? Diese Frage hat bei meinen Studierenden jeweils anhaltende Diskussionen ausgelšst.

Abb. 9: Schubspiegelsymmetrie?

5.2    Reifen

Auch der Abdruck eines Reifens hat Schubspiegelsymmetrie.

Problem 3: In welcher Richtung fuhr der Traktor (Abb. 10)?

Abb. 10: In welcher Richtung fuhr der Traktor?

5.3    Quadratraster und Schachbrettmuster

Die Abbildung 11a zeigt exemplarisch die drei Typen der Symmetrieachsen im Quadratraster (Mittellinien, Rasterlinien, Diagonalen).

Im  zugehšrigen Schachbrettmuster sind aber die Rasterlinien keine Symmetrieachsen mehr, sondern ãnurÒ Schubspiegelachsen.

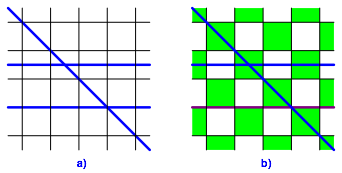
Abb. 11: Symmetrieachsen und Schubspiegelachse

Es gibt aber auch im Quadratraster reine Schubspiegelachsen (Abb. 12a). Im Schachbrettmuster ist die entsprechende Linie weder Symmetrieachse noch Schubspiegelachse (Abb. 12b).

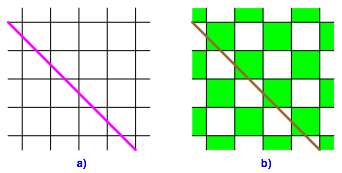
Abb. 12: Schubspiegelachse und gar nichts

Dieses unterschiedliche Verhalten in den Abbildungen 11 und 12 fŸhrt zur folgenden Frage.

Problem 4: Gehšren Quadratraster und Schachbrettmuster zur gleichen Symmetrieklasse?

5.4    Zusammensetzung von Schubspiegelungen

Die Abbildung 13a gibt die relevanten Daten (Achse und Schubvektor) von zwei Schubspiegelungen. In der Abbildung 13b ist die Zusammensetzung exemplarisch durchgefŸhrt. Das Urbilddreieck ist grŸn, das finale Bilddreieck rot. Die Abbildung von grŸn nach rot ist offensichtlich eine Drehung.

Problem 5: Wie finden wir aus den Daten der Abbildung 13a den Drehwinkel und das Drehzentrum dieser Drehung?

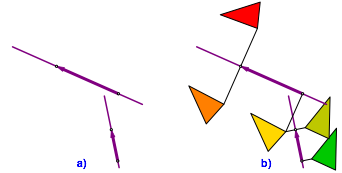
Abb. 13: Zusammensetzung zweier Schubspiegelungen

6     Beweis unseres Theorems

Die Abbildung 14a zeigt die Abbildung 7b mit weiteren Schubspiegelachsen. Mit Hilfe des Klassifizierungsschemas im Anhang finden wir dass dieses FlŠchenornament zur Symmetrieklasse pgg gehšrt.

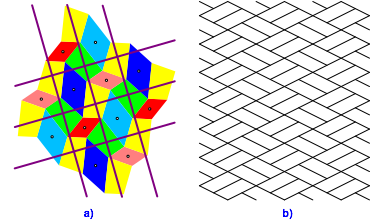
Abb. 14: Symmetrieklasse pgg

Die Abbildung 14b zeigt das ãschulmŠ§igeÒ FlŠchenornament zu dieser Symmetrieklasse.

FŸr diese Symmetrieklasse gilt gemŠ§ Tabelle 1:

pgg

Keine Symmetrieachsen. Orthogonale Schubspiegelachsen. Dazwischen zweizŠhlige Drehzentren. Rechteckgitter

Damit ist unser Theorem bewiesen.

7     Bemerkungen zu den Problemen

Problem 1: Offene Aufgabe.

Problem 2: Die Fu§spur eines Hinkenden hat keine Schubspiegelsymmetrie.

Problem 3: Der Traktor fuhr nach links.

Problem 4: Quadratraster und Schachbrettmuster gehšren zur gleichen Symmetrieklasse. Um dies einzusehen, muss eine der beiden Figuren um 45¡ verdreht werden.

Problem 5: Kann mit Spiegelungsgeometrie bearbeitet werden [4].

 

Dank

Der Autor dankt E.V., M. fŸr viele Ideen und Anregungen.

Anhang

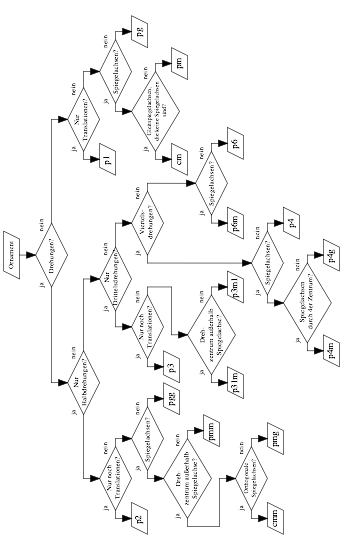
Klassifizierungshilfe

Literatur

Niggli, Paul (1924): Die FlŠchensymmetrien homogener Kontinuen. Zeitschrift fŸr Kristallographie und Mineralogie, Band 60, 283-298.

P—lya, George (1924): †ber die Analogie der Kristallsymmetrie in der Ebene. Zeitschrift fŸr Kristallographie und Mineralogie, Band 60, 278-282.

 

Websites

 [1] Wallpaper Patterns (13.03.2017)

http://mathstat.slu.edu/escher/index.php/Wallpaper_Patterns

 

[2] Morandi, Patrick J. (2007): Symmetry Groups: The Classification of Wallpaper Patterns (13.03.2017)

http://sierra.nmsu.edu/morandi/OldWebPages/Math526Spring2007/Math526text2007-01-10.pdf

 

[3] Wikipedia: Ebene kristallographische Gruppe (13.03.2017)

https://de.wikipedia.org/wiki/Ebene_kristallographische_Gruppe

 

[4] Walser: Schubspiegelungen zusammensetzen (05.04.2017)

www.walser-h-m.ch/hans/Miniaturen/S/Schubspiegelungen_zusammensetzen/Schubspiegelungen_zusammensetzen.htm