Hans Walser

Perspektivenwechsel

 

 

 

Forum fŸr Begabtenfšrderung 


14. Bis 16. MŠrz 2019, TU Braunschweig 

 

 

 

Zusammenfassung. Die Umkehrung einer klassischen Schulaufgabe (Sekundarstufe) fŸhrt zu einer Verallgemeinerung der Begriffe ãThaleskreisÒ und ãOrtsbogenÒ.

 

Last modified 8. MŠrz 2019.

1   Wie das Problem entstand

Eine klassische Aufgabe im Abiturtraining geht so (vgl. etwa Weber und Zillmer 2002, S. 66, Aufg. DA 32) :

Gegeben sind ein Punkt  und eine Parabel  (Abb. 1a). Gesucht sind die Tangenten von diesem Punkt an die Parabel sowie der eingeschlossene Winkel (Abb. 1b).

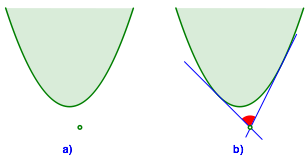
Abb. 1: Die klassische Aufgabe

Nun kann man die Frage umkehren: Wir geben nicht den Punkt P sondern den Schnittwinkel vor und suchen nach den passenden Punkten P.

2   Lšsung der Schulaufgabe

ZunŠchst lšsen wir die Schulaufgabe.

Es gibt zwei Herangehensweisen:

Erster Lšsungsweg: Wir nehmen alle Geraden durch den Punkt P und wŠhlen dann diejenigen aus, welche die Parabel p berŸhren (Abb. 2a).

Zweiter Lšsungsweg: Wir nehmen alle Tangenten an die Parabel p und wŠhlen diejenigen aus, welche durch den Punkt P verlaufen (Abb. 2b).

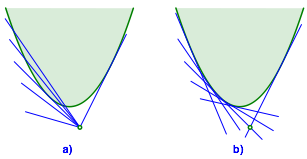
Abb. 2: Herangehensweisen

2.1  Erster Lšsungsweg

Das GeradenbŸschel durch  wird beschrieben durch:

 

                                                                                       (1)

 

 

 

Dabei ist m die Steigung der jeweiligen BŸschelgeraden.

Der Schnitt mit der Parabel  fŸhrt auf die quadratische Gleichung:

 

                                                                                                       (2)

 

 

Eine quadratische Gleichung hat zwei, genau eine oder keine Lšsungen. Im ersten Fall schneiden die BŸschelgerade die Parabel, im zweiten Fall ist sie Tangente und im dritten Fall geht sie neben der Parabel durch. Die Anzahl der Lšsungen hŠngt von der so genannten Diskriminante D der quadratischen Gleichung ab.

 

                                                                                                       (3)

 

 

FŸr den Fall der Tangenten muss D = 0 sein, also:

 

                                                                                                                (4)

 

 

Diese quadratische Gleichung (4) hat in unserem Beispiel zwei Lšsungen, nŠmlich:

 

                                                                                                   (5)

 

 

Dies sind die Steigungen der beiden gesuchten Tangenten. Aus (1) ergeben sich deren Gleichungen:

 

                                                                                           (6)

 

 

FŸr den Schnittwinkel finden wir:

 

                                                                                     (7)

 

 

Dieser Lšsungsweg benštigt nur quadratische Gleichungen und Trigonometrie.

2.2  Zweiter Lšsungsweg

Die Tangente im Parabelpunkt  hat die Parameterdarstellung:

 

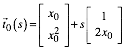                                                                                                (8)

 

 

 

Aus

 

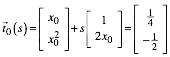                                                                                 (9)

 

 

 

 

ergeben sich die beiden Gleichungen:

 

                                                                                                             (10)

 

 

 

Elimination von s fŸhrt auf die quadratische Gleichung

 

                                                                                                           (11)

 

 

mit den beiden Lšsungen:

 

                                                                                                 (12)

 

 

Somit erhalten wir die beiden Tangenten:

 

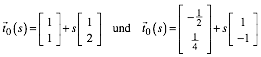                                                 (13)

 

 

 

 

Dies entspricht den Lšsungen (6).

Dieser Lšsungsweg benštigt den Tangentialvektor und damit die Differentialrechnung. Wir haben aber auch eine quadratische Gleichung.

2.3  Gibt es einen geometrischen Lšsungsweg?

Den gibt es, und er ist verfahrensmŠ§ig sehr einfach. Er funktioniert im Prinzip fŸr alle Kegelschnitte.

2.3.1 Parabel

Wir arbeiten mit dem Brennpunkt F und der Leitlinie l der Parabel p (Abb. 3a).

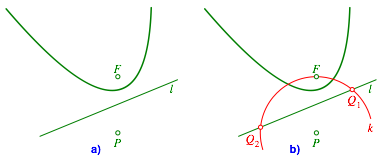
Abb. 3: Parabel. Erster Schritt

Wir schneiden den Kreis k um P durch F und mit der Leitlinie l in Q1 und Q2 (Abb. 3b).

Die Mittelsenkrechten der Strecken FQ1 und FQ2 sind die gesuchten Tangenten t1 beziehungsweise t2 (Abb. 4a).

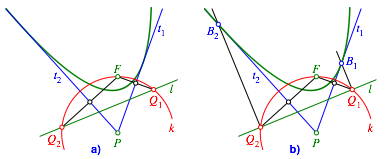
Abb. 4: Parabeltangenten

Die BerŸhrungspunkte liegen auf den Loten zur Leitlinie l durch Q1 und Q2 (Abb. 4b).

Diese Konstruktion folgt aus der Abstandsdefinition und der Reflexionseigenschaft der Parabel.

Das Viereck PQ1B1F ist ein Drachenviereck mit der Tangente t1 als Symmetrieachse (Abb. 5a). Der Diagonalenschnittpunkt D1 liegt auf der Scheiteltangente tS der Parabel. Analog fŸr die andere Tangente (Abb. 5b).

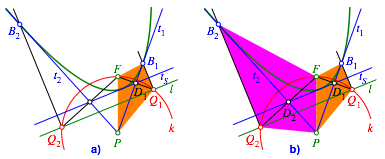
Abb. 5: Drachenvierecke

2.3.2 Ellipse

Die Tangentenkonstruktion fŸr die Ellipse geht im Prinzip analog. Von einer Ellipse e seien die beiden Brennpunkte F1 und F2 sowie die LŠnge 2a der langen Achse bekannt (Abb. 6a).

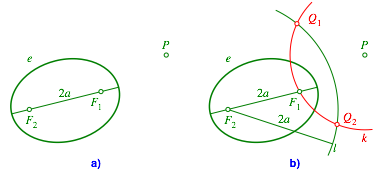
Abb. 6: Ellipse

Als ersten Schritt zeichnen wir einen Kreis l mit dem Zentrum F2 und dem Radius 2a (dieser Kreis entspricht der Leitlinie der Parabel) sowie einen Kreis k um P durch den anderen Brennpunkt F1. Die Schnittpunkte der beiden Kreise bezeichnen wir mit Q1 und Q2 (Abb. 6b).

Die Mittelsenkrechten der Strecken F1Q1 und F1Q2 sind die gesuchten Tangenten t1 beziehungsweise t2 (Abb. 7a). Die BerŸhrungspunkte liegen auf den Strecken F2Q1 und F2Q2 (Abb. 7b).

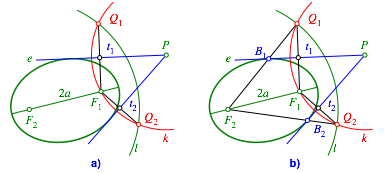
Abb. 7: Ellipsentangenten

Wieder gibt es Drachenvierecke (Abb. 8). Deren Diagonalenschnittpunkte liegen auf dem Thaleskreis kS Ÿber der langen Ellipsenachse. Dieser Kreis berŸhrt die Ellipsen in den beiden spitzen Scheiteln.

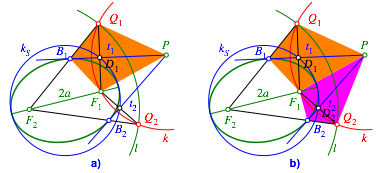
Abb. 8: Drachenvierecke bei der Ellipse

Bemerkung 1: Die Konstruktion ist asymmetrisch, indem die beiden Brennpunkte unterschiedlich verwendet werden. Die Abbildung 9a zeigt die Konstruktion mit vertauschten Rollen der beiden Brennpunkt, die Abbildung 9b die †berlagerung der beiden Lšsungswege.

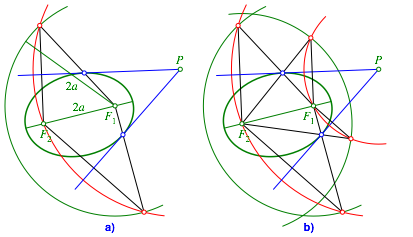
Abb. 9: Vertauschte Rollen. †berlagerung

Aus dieser SymmetrieŸberlegung lŠsst sich eine Tangentenkonstruktion ableiten, welche ohne Mittelsenkrechte auskommt.

Bemerkung 2: Die in der Schule Ÿbliche Konstruktion der Ellipsentangente benutzt die AffinitŠt. Die Ellipse wird affin zu einem Kreis aufgeblasen (Abb. 10a), dabei wird der Punkt P mitgenommen. Dann werden die Kreistangenten gezeichnet und anschlie§end das Ganze rŸckwŠrts abgebildet (Abb. 10b).

Unsere Konstruktion verwendet keine AffinitŠt.

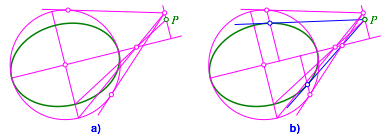
Abb. 10: Konstruktion mit AffinitŠt

Bemerkung 3: Wenn der Brennpunkt F2 (nach links) ins Unendliche abrauscht ergibt sich aus der Abbildung 7 die Situation der Parabel.

Bemerkung 4: Wenn wir die beiden Brennpunkte F1 und F2 zusammenfallen lassen, ergibt sich eine einfache Tangentenkonstruktion an den Kreis, welche ohne den Thaleskreis auskommt.

2.3.3 Hyperbel

Die Konstruktion geht všllig analog zur Ellipse. Die Abbildungen 11, 12 und 13 zeigen den Konstruktionsablauf.

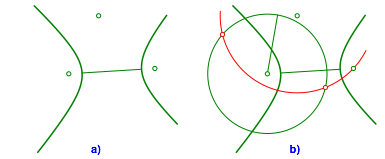
Abb. 11: Hyperbel

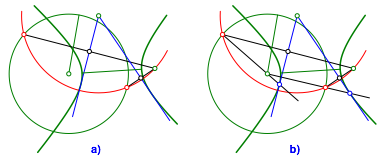
Abb. 12: Hyperbeltangenten

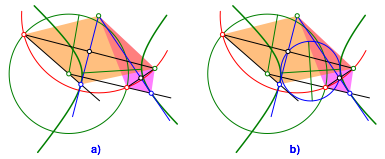
Abb. 13: Drachenvierecke bei der Hyperbel

3   Umkehrung

Umkehrung

Von welchen Punkten aus sehen wir die Parabel unter einem vorgegebenen Winkel?

3.1  Gibt es Šhnliche Fragen?

Von welchen Punkten aus sehen wir eine Strecke unter einem vorgegebenen Winkel? Die Lšsung ist das Ortsbogenpaar, im Sonderfall des rechten Winkels der Thaleskreis.

Wir kšnnen die Strecke durch ein Polygon ersetzen: von welchen Punkten aus sehen wir das regelmŠ§ige Siebeneck (Abb. 16a) unter einem Winkel von 60¡? Die Lšsung ist der Au§enrand der Kreisfiguration der Abbildung 16b. Die Kreise sind Ortsbogen fŸr den Winkel 60¡ Ÿber den Diagonalen des Siebenecks.

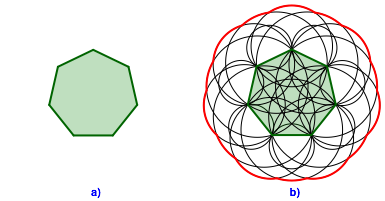
Abb. 16: RegelmŠ§iges Siebeneck gesehen unter 60¡

Dom zu Mainz. RegelmŠ§iges Siebeneck

Die Abbildung 17a zeigt zwei verschiedene allgemeine FŠlle, die Abbildung 17b einen Sonderfall.

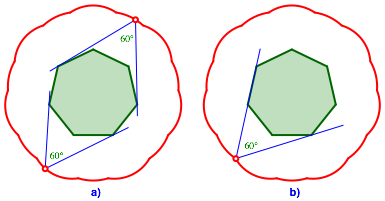
Abb. 17: Verschiedene FŠlle

Wir werden im Folgenden die Parabel auf Kegelschnitte verallgemeinern: von welchen Punkten aus sehen einen Kegelschnitt unter einem vorgegebenen Winkel? ZunŠchst untersuchen wir die Situation fŸr rechte Winkel (Thalesproblem).

4   Rechte Winkel als Sehwinkel. Orthoptische Kurven

Von welchen Punkten aus sehen wir einen Kegelschnitt unter einem rechten Winkel? Die Menge dieser Punkte wird als orthoptische Kurve bezeichnet (Odehnal, 2010).

4.1  Kreis

Der Fall des Kreises ist einfach. Wir erhalten einen Kreis, dessen Radius -mal so gro§ ist wie der Radius des gegebenen Kreises (Abb. 18):

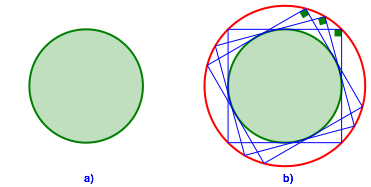
Abb. 18: Kreis und rechte Winkel

4.2  Parabel

Die Lšsung ist die Leitlinie der Parabel (Abb. 19). Der Beweis ist eine schšne †bung in Parabelgeometrie.

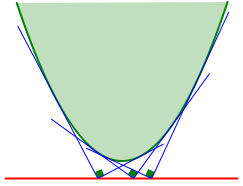
Abb. 19: Parabel und Leitlinie

Die Leitlinie ist also sozusagen der ãThaleskreisÒ der Parabel.

4.3  Ellipse

Wir erhalten interessanterweise einen Kreis (Abb. 20). Bei einer Ellipse mit den Halbachsen a und b hat dieser Kreis den Radius r:

 

                                                                                                                 (14)

 

 

Die othoptische Kurve (ãThaleskreisÒ) einer Ellipse ist also ein Kreis. FŸr den Beweis siehe [3]. Der Beweis ist recht happig.  

Die Ecken der ãUmrechteckeÒ einer Ellipse liegen auf einem Kreis.

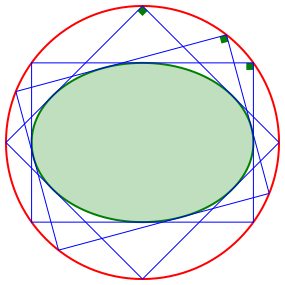
Abb. 20: Ellipse und Thaleskreis

SonderfŠlle:

a)   FŸr b = 0 wird die Ellipse zu einer Strecke und wir erhalten den gewšhnlichen Thaleskreis.

b)  FŸr a = b ist die Ellipse ein Kreis und wir erhalten den Sonderfall der Abbildung 5.

4.4  Hyperbel

Die orthoptische Kurve existiert nur fŸr  und ist ebenfalls ein Kreis (Abb. 21). Dieser Kreis hat den Radius r:

 

                                                                                                                 (15)

 

 

FŸr den Beweis siehe [3]. FŸr  liegen die HyperbelŠste im spitzwinkligen Bereich der Asymptoten (Abb. 21).

Die Asymptoten zerlegen den Kreis in zwei kleine Bšgen im spitzwinkligen Bereich und zwei gro§e Bšgen im stumpfwinkligen Bereich.

Abb. 21: Hyperbel und Thaleskreis

Die von Punkten auf einem kleinen Bogen des Kreises ausgehenden Tangenten berŸhren beide denselben Hyperbelast. Dieser Hyperbelast liegt im Innern des Rechtwinkelbereiches der beiden Tangenten.

Die von Punkten auf einem gro§en Bogen des Kreises ausgehenden Tangenten berŸhren beide HyperbelŠste. Die beiden HyperbelŠste liegen au§erhalb des Rechtwinkelbereiches der beiden Tangenten. Um die Hyperbel zu sehen, brŠuchte es eine Fischaugenkamera.

FŸr die Punkte des Kreises auf den Asymptoten haben wir einen interessanten Sonderfall (Abb. 22).

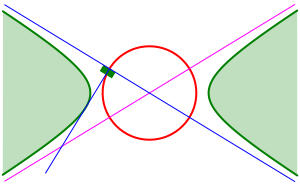
Abb. 22: Sonderfall auf den Asymptoten

FŸr den Sonderfall  (gleichseitige Hyperbel) schrumpft der Kreis zu einem Punkt und die ãTangentenÒ sind die Asymptoten.

 

5   Beliebige Winkel als Sehwinkel

Wir bezeichnen den vorgegebenen Sehwinkel mit . Der Winkel  ist also der halbe Sehwinkel. Diese Schreibweise vereinfacht die folgenden Formeln. Die Menge der Punkte, von denen aus das Objekt unter einem beliebigen vorgegebenen Winkel gesehen werden kann, wird als isoptische Kurve bezeichnet (Odehnal 2010).

5.1  Kreis

Der Fall ist trivial. Wir erhalten einen Kreis. Sein Radius ist das -fache des ursprŸnglichen Kreisradius.

5.2  Parabel

5.2.1 Allgemein

Die gesuchten Punkte liegen auf einem Hyperbelast (Abb. 23).

Auf dem zweiten Hyperbelast (magenta in Abb. 23) liegen die Punkte, von denen aus die Parabel unter dem Winkel  gesehen wird.

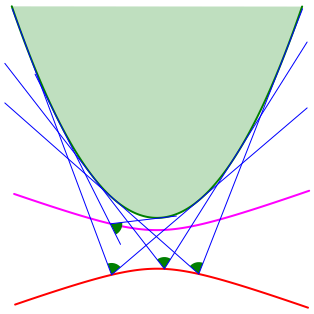
Abb. 23: Parabel und Hyperbelast

FŸr den rechnerischen Nachweis arbeitete ich mit der Parabel p:

 

                                                                                                                     (16)

 

 

Die Parabel p hat den Brennpunkt  und die Leitlinie .

Vorgehen zum Auffinden der Lšsung:

a)     Auf Grund von Beispielen vermuten wir, dass es sich um eine querliegende Hyperbel handelt. Der untere Hyperbelast ist dabei die Lšsung fŸr einen spitzen Winkel , der obere Hyperbelast die Lšsung fŸr seinen stumpfen Nebenwinkel. Der eine Brennpunkt der Hyperbel fŠllt mit dem Brennpunkt der Parabel p zusammen

b)    Berechnung einzelner Punkte (mit Symmetrie-†berlegungen). Es werden die Scheitelpunkte  und  der Hyperbel berechnet.

c)     Berechnung der Hyperbelgleichung.

d)    Verifikation, dass Lšsung. Diesen letzten Schritt habe ich mit DGS gemacht.

e)     Andere Lšsungen mit einer NiveaulinienŸberlegung ausschlie§en.

Zu b): Wir berechnen den zu einem spitzen Winkel  gehšrenden Scheitelpunkt  der Hyperbel. Hilfreich dazu ist der in der Abbildung 24 in orange eingezeichnete Rhombus. Er ergibt sich aus der Brennpunkt-Leitlinie-Definition der Parabel und der Reflexionseigenschaft der Parabeltangente. Seine Ecken sind der Brennpunkt , der BerŸhrungspunkt der Tangente an die Parabel, der Lotfu§punkt auf die Leitlinie und der Punkte  auf der y-Achse. Der Rhombus hat den spitzen Winkel . Sein Mittelpunkt liegt auf der x-Achse.

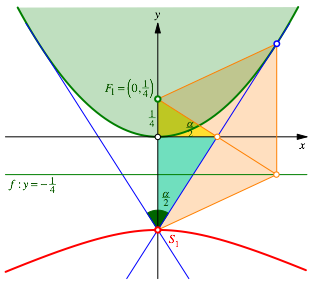
Abb. 24: Scheitelpunkt

Mit Hilfe der gelb und zyan eingezeichneten rechtwinkligen Dreiecke ergibt sich (man beachte die Kontangens-Funktion):

 

                                                                                                     (17)

 

 

Analog ergibt sich fŸr den Scheitelpunkt :

 

                                                                                                     (18)

 

 

Mit dem Brennpunkt  und den beiden Scheitelpunkten  und  haben wir jetzt ausreichend Informationen zur Bestimmung der Hyperbel.

Wir erhalten:

Zweiter Brennpunkt:

 

                                                                           (19)

 

 

Achsen:

 

                                              (20)

 

 

Mittelpunkt:

 

                                                             (21)

 

 

Hyperbelgleichung:

 

                                                                                             (22)

 

 

 

Nun kšnnen wir von einem Punkt auf der Hyperbel (21) ausgehend die Tangenten an die Parabel (15) anlegen und feststellen, dass deren Zwischenwinkel  ist.

Die Abbildung 25 zeigt die Hyperbelschar fŸr . Die Kurven sind eine Art Niveaulinien fŸr . Die Schrittweite ist .

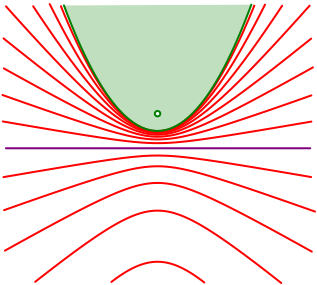
Abb. 25: Hyperbelschar als isoptische Kurven

5.2.2 Schulbeispiel

Gesucht ist die Menge der Punkte, von denen aus die Parabel  unter einem Winkel von 60¡ gesehen wird.

GemŠ§ (20) und (21) erhalten wir die Hyperbel:

 

                                                                                             (23)

 

 

Die Abbildung 26 zeigt die Situation.

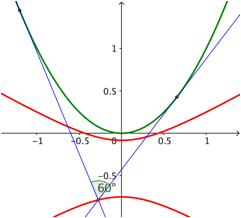
Abb. 26: Schulbeispiel

5.3  Ellipse

Die Abbildung 27 zeigt die Situation bei der Ellipse. Die Schrittweite ist wiederum 15¡.

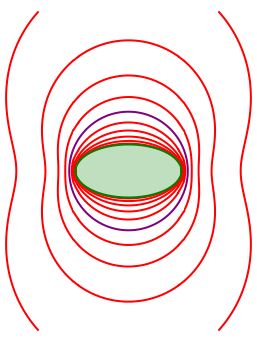
Abb. 27: Isoptische Kurven der Ellipse

Die isoptischen Kurven sind keine Kegelschnitte mehr, sondern Kurven vierten Grades.

5.4  Hyperbel

Die Abbildung 28 zeigt die Situation bei der Hyperbel. Die Schrittweite ist wiederum 15¡.

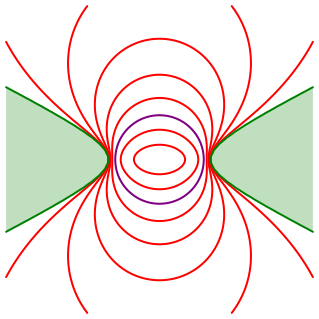
Abb. 28: Isoptische Kurven der Hyperbel

 

Dank

Der Autor dankt Kolleginnen und Kollegen des Liechtensteinischen Gymnasiums Vaduz fŸr Anregungen und Hinweise.

Websites

[1] Hans Walser: Sehwinkel bei Kegelschnitten (abgerufen 15.06.2018):

www.walser-h-m.ch/hans/Miniaturen/S/Sehwinkel_Kegelschnitte/Sehwinkel_Kegelschnitte.htm

 

[2] Hans Walser: Tangente an Kegelschnitt (abgerufen 03.06.2018):

www.walser-h-m.ch/hans/Miniaturen/T/Tangente_an_Kegelschnitt/Tangente_an_Kegelschnitt.htm

 

[3] Hans Walser: Thaleskreis an Ellipse und Hyperbel (abgerufen 15.06.2018):

www.walser-h-m.ch/hans/Miniaturen/T/Thaleskreis_E_H/Thaleskreis_E_H.htm

 

[4] Hans Walser: Kreistangente ohne Thaleskreis (abgerufen 18.06.2018):

www.walser-h-m.ch/hans/Miniaturen/K/Kreistangente_o_Tk/Kreistangente_o_Tk.htm

 

[5] Hans Walser: Tangente an Ellipse und Hyperbel (abgerufen 19.06.2018):

www.walser-h-m.ch/hans/Miniaturen/T/Tangenten_E_H/Tangenten_E_H.htm

 

 

Literatur

Odehnal, Boris (2010): Equioptic Curves of Conic Sections. In: Journal for Geometry and Graphics. Band 14, 2010, Nr. 1, S. 29–43.

Weber, Karlheinz und Zillmer, Wolfgang (2002): Mathematik Gymnasiale Oberstufe. Grundkurs Aufgabenbuch. Analysis, Analytische Geometrie und Lineare Algebra. Stochastik. Berlin – Frankfurt M: Duden Paetec Schulbuchverlag. ISBN 3-89818-110-3.