Streifen

 

 

 

 

 

 

30. Tag fŸr Mathematik und Unterricht

Mittwoch, 11. September 2019
Kantonsschule Frauenfeld

Hans Walser

www.walser-h-m.ch/hans

 

Streifen

Mit Plastikstreifen aus der Verpackungsindustrie bauen wir zunŠchst ein ebenes hexagonales Geflecht. Einfache Modifikationen fŸhren zur Kugelgeometrie einerseits und zur hyperbolischen Geometrie andererseits. Ersetzen der Plastikstreifen durch Papierstreifen fŸhrt zu Modellen der regulŠren Polyeder.

Im Unterricht werden verschiedene Kompetenzen gefšrdert, allen voran das rŠumliche und das sphŠrische Vorstellungsvermšgen, aber auch das Design eines Arbeitsvorgangs und die soziale Interaktion. Nicht zuletzt genaues Arbeiten.

Der Vortrag basiert auf Erfahrungen mit SchŸlerinnen und SchŸlern hauptsŠchlich der Sekundarstufe, aber auch in der Grund- und Weiterbildung von Lehrpersonen.

Querbeziehungen zu Kristallsystemen (Chemie) und zu ZahlenrŠtseln.

1     Starten und landen

In der Sekundarschule (Schweiz, fŸnfziger Jahre) gab es (nur fŸr Knaben) ein Fach ãtechnisches ZeichnenÒ. Da musste mit Tusche und Rei§feder gearbeitet werden. Wie beim Fliegen gab es beim Zeichnen einer Strecke zwei kritische Momente: Anfang und Ende. An beiden Stellen hatte die Rei§feder die Tendenz, einen ãTolggenÒ (Klecks) abzusetzen.

Die Aufgabe, ein Bienenwabenmuster (regulŠres Hexagonnetz) zu zeichnen, erweist sich wegen der vielen kurzen Strecken als Alptraum. Das Problem kann allerdings entschŠrft werden, wenn wir die Kantenmitten des Hexagonnetzes geradlinig verbinden. Dann erhalten wir ein halbregulŠres Netz aus Sechsecken und Dreiecken, und die Linien kšnnen durchstarten.

Hexagonnetz und Netz mit Sechsecken und Dreiecken

Dieses halbregulŠre Netz kann mit Plastikstreifen (aus der Verpackungsindustrie) und Rundkopfklammern realisiert werden. Aus Šsthetischen GrŸnden geben wir uns MŸhe, die Plastikstreifen wie bei einem Geflecht abwechslungsweise oben und unten laufen zu lassen.

     

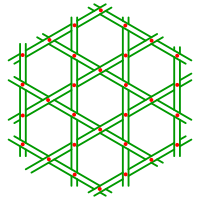
Streifenmodell. Flechtstruktur

2     Immer gerade aus

... so geh hŸbsch sittsam und lauf nicht vom Wege ab!

Die Plastikstreifen und Papierstreifen sind zwar biegsam, aber nur nach oben und unten, hingegen praktisch nicht in seitlicher Richtung. Sie laufen ãsubjektivÒ gerade aus.

Immer der Nase nach

In der Geometrie werden Linien ohne seitliche KrŸmmung als geodŠtische Linien bezeichnet. In der ebenen Geometrie sind das die Geraden, auf der Kugel die Gro§kreise.

3     Von Sechsecken zu FŸnfecken

3.1   Die Halbkugel

Nun versuchen wir, in unserem Flechtmodell durch …ffnen einiger Rundkopfklammeren und Entfernen einiger Streifen sŠmtliche Sechsecke auf FŸnfecke zu reduzieren. Die Dreiecke lassen wir bestehen, es reduziert sich allerdings deren Anzahl. Bei diesem Prozess wšlbt sich das Modell aus der Ebene heraus, und es entsteht eine Halbkugel aus nur noch sechs FŸnfecken und zehn Dreiecken. Es ist da einiges auf der Strecke geblieben.

    

Halbkugel. Stereografisches Bild

Wir denken uns den hšchsten Punkt der Halbkugel (also den Mittelpunkt des obersten FŸnfeckes) als Nordpol und schauen nun die Sache vom SŸdpol aus (also von unten her) an. Dann sehen wir das so genannte stereografische Bild der Halbkugel. Wir sehen, dass die auf der Halbkugel kongruenten regelmŠ§igen FŸnfecke und gleichseitigen Dreiecke im stereografischen Bild verzerrt erscheinen. Das stereografische Bild hat die Eigenschaft, dass zwar die LŠngen verzerrt werden, aber die Winkel ãechtÒ, also unverzerrt, erscheinen. Beim mittleren FŸnfeck (das ist das Bild des obersten FŸnfeckes auf der Halbkugel) sind die Seiten etwas nach au§en gebogen, die einzelnen Winkel und damit die Winkelsumme also etwas grš§er als beim ebenen FŸnfeck. Damit sind wir bei einer wichtigen Eigenschaft der sphŠrischen Geometrie angelangt: Die Winkelsumme der sphŠrischen Polygone ist grš§er als die Winkelsumme der entsprechenden Polygone in der ebenen Geometrie.

3.2   Ganze Kugel

NatŸrlich kšnnen wir die Halbkugel zur ganzen Kugel erweitern. Beim stereografischen Bild werden nun die Verzerrungen noch drastischer. Die nšrdliche Halbkugel wird auf das Innere des kleinen Kreises abgebildet, die sŸdliche auf das ganze €u§ere. Der kleine Kreis ist das Bild des €quators und in Wirklichkeit, das hei§t im Kugelmodell, gleich gro§ wie die fŸnf anderen Kreise.

    

Ganze Kugel und stereografisches Bild

Wir zŠhlen zwšlf FŸnfecke, wobei im stereografischen Bild das zwšlfte FŸnfeck das gesamte €u§ere der Figur ist, und 20 Dreiecke. Diese Anzahlen erinnern an die platonischen Kšrper. Aus zwšlf FŸnfecken kann das Dodekaeder gebaut werden, aus 20 Dreiecken das dazu duale Ikosaeder.

FŸr das Kogelmodell benštigen wir sechs Streifen, fŸr jeden Gro§kreis einen.

Sechs Streifen

Die Streifen werden je durch 11 Lšcher in regelmŠ§igen AbstŠnden in 10 gleiche Strecken unterteilt. Die SeitenlŠngen der FŸnfecke und der Dreiecke sind also  des Kugelumfanges. Das letzte Loch kommt durch das Schlie§en zum Kreis auf das erste zu liegen. Wir haben also effektiv noch 60 Lšcher und brauchen beim Zusammenbau daher 30 Rundkopfklammern, da bei jedem Kreuzungspunkt zweier Streifen eine Rundkopfklammer eingesetzt wird. Es gilt die Beziehung:

 

# FŸnfecke – # Rundkopfklammern + # Dreiecke = 12 – 30 + 20 = 2

 

Papierstreifenmodell des Dodekaeders

Sechs-Streifen-Kugel und Dodekaeder

Das Papierstreifenmodell des Dodekaeders hat dieselbe Struktur wie die Sechs-Streifen-Kugel.

3.3   Diagonalen

Nun Ÿberlegen wir uns, wie die Diagonalen der FŸnfecke laufen. Wir kšnnen eine Diagonale Ÿber Eck ins benachbarte FŸnfeck fortsetzen und kommen nach 6 FŸnfecken wieder zurŸck. Die DiagonalenlŠnge ist  des Kugelumfanges.

Wir kšnnen daher mit zehn Streifen mit einer Sechserteilung die Diagonalen dem Kugelmodell dazufŸgen. 

Streifen fŸr eine Diagonale

Kugel und Kugel mit Diagonalen

Auf der Kugel haben wir fŸr unsere FŸnfecke das VerhŠltnis:

 

 

 

 

Das ist etwas mehr als beim ebenen FŸnfeck, wo wir das VerhŠltnis des goldenen Schnittes haben (Walser 2013):

 

 

 

 

Die folgenden Abbildungen zeigen den ebenen Fall mit dem Goldenen Schnitt und den gewšlbten Fall mit den etwas lŠngeren Diagonalen, welche zur Wšlbung fŸhren.

Flach und gewšlbt

Noch ein Wort zur Vorsicht. Das VerhŠltnis  gilt nur fŸr KugelfŸnfecke dieser Grš§e, also bei einer Kombination von zwšlf FŸnfecken mit 20 Dreiecken. Bei kleineren FŸnfecken auf derselben Kugel wird das VerhŠltnis kleiner und nŠhert sich dem goldenen Schnitt an, weil ja auch die FŸnfecke immer mehr sich einem ebenen FŸnfeck annŠhern. In der Kugelgeometrie haben wir keine €hnlichkeit.

3.4   Nur Diagonalen

Das Kugelmodell ist sogar stabil, wenn wir nur die Diagonalen zur Kugel zusammenfŸgen.

Diagonalen. Lampenschirm

4     Von Sechsecken zu FŸnfecken zu Vierecken

4.1   Modell und Diagonalen

Nun reduzieren wir weiter zu Vierecken. Wir erhalten ein Kugelmodell aus vier Streifen, das aus 6 Vierecken und 8 Dreiecken besteht. Diese Zahlen erinnern an WŸrfel und Oktaeder.

6 Vierecke und 8 Dreiecke

Wir kšnnen wiederum Diagonalen einfŸgen. Es gilt:

 

 

 

 

Die Diagonalen sind wiederum lŠnger als im ebenen Fall, wo wir das VerhŠltnis  haben.

FŸr das Modell benštigen wir vier Streifen zu je 6 Einheiten.

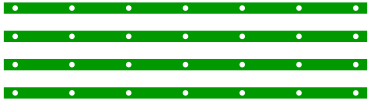
Vier Streifen

Wir brauchen zwšlf Rundkopfklammern. Es gilt die Beziehung:

 

# Vierecke – # Rundkopfklammern + # Dreiecke = 6 – 12 + 8 = 2

 

4.2   Papierstreifenmodell des WŸrfels

Wir kšnnen aus vier Papierstreifen ein Modell des WŸrfels flechten, das dieselbe Struktur wie die Vier-Streifen-Kugel hat. Die Papierstreifen laufen diagonal von Kantenmitte zu Kantenmitte.

Papierstreifenmodell des WŸrfels

4.3   Kugelcluster

Mehrere baugleiche Kugeln kšnnen zu einem Kugelcluster zusammengefŸgt werden, wobei genau die Rundkopfklammern als VerbindungsstŸcke dienen.

Tetraeder und Oktaeder

WŸrfel und Pyramide

Wenn wir uns die Kugelcluster fortgesetzt denken, ergibt sich eine schon von Kepler vermutete dichteste Kugelpackung. Gau§ hat 1831 bewiesen, dass diese Kugelpackung unter allen regulŠren Kugelpackungen optimal ist. Thomas Hales bewies die Keplersche Vermutung 1998/2005 mit einem Computerbeweis und 2014 mit einem formalen Beweissystem.

Im Unterricht kšnnen Kugelpyramiden mit Glaskugeln realisiert werden. Eine geeignete Unterlage vermeidet das Wegrollen.

Pyramide mit Glaskugeln

5     Von Sechsecken zu FŸnfecken zu Vierecken zu Dreiecken

5.1   Kugelmodell

Wenn wir zu Dreiecken reduzieren, erhalten wir eine Kugel mit vier Dreiecken und vier Dreiecken. Das ist sprachlich korrekt so, indem die ersten vier Dreiecke aus der Reduktion der Vierecke entstanden sind, die zweiten vier Dreiecke zu den Dreiecken gehšren, die schon immer da waren. Wir erhalten ein Kugelmodell aus drei Kreisen.

Drei Kreise. Kugelcluster

FŸr den Zusammenbau der drei Streifen benštigen wir 6 Rundkopfklammern.

Drei Streifen

Es gilt die Beziehung:

 

# Dreiecke – # Rundkopfklammern + # Dreiecke = 4 – 6 + 4 = 2

 

5.2   Stereografische Projektion und magische Kreise

Stereografische Projektion und magische Kreise

Aus der stereografischen Projektion kann ein ZahlenrŠtsel abgeleitet werden. In die kleinen Kreise sind die Zahlen 1 bis 6 einzusetzen so, dass auf jedem der drei gro§en Kreise die Zahlensumme gleich ist.

Das RŠtsel kann mit einer Symmetrie-†berlegung angegangen werden. Die Gesamtsumme der Zahlen von 1 bis 6 ist 21, der Mittelwert also 3.5. Wenn wir uns einen Kreis wegdenken, bleiben noch deren zwei Ÿbrig. In den beiden Schnittpunkten muss durchschnittlich der Wert 3.5 eingesetzte werden, also die Summe 7. Dies kann durch eines der drei Paare 1+6, 2+5 oder 3+4 geschehen.


5.3   Der SpielwŸrfel. Polyeder

Die Lšsung des ZahlenrŠtsels erinnert an die Augenverteilung auf einem SpielwŸrfel.

  

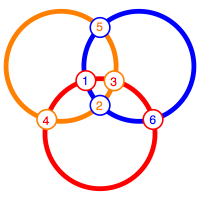
Lšsung und SpielwŸrfel

Den SpielwŸrfel kšnnen wir aus drei Papierstreifen flechten. Jeder der drei Streifen besteht aus vier Quadraten sowie zwei zur Stabilisierung benštigten Zusatzquadraten.

    

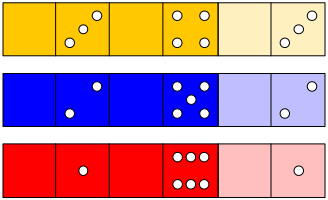
Drei Streifen fŸr den WŸrfel

6     Von Sechsecken zu Siebenecken

Wenn wir die Sechsecke durch Siebenecke ersetzen, krŸmmt sich das Modell hyperbolisch in den Raum. Bei dieser KrŸmmungsart haben wir KrŸmmungen nach oben und nach unten. Im entsprechenden Ausschnitt aus dem Kreismodell von PoincarŽ sehen wir die NachbarschaftsverhŠltnisse der Siebenecke und der Dreiecke.

    

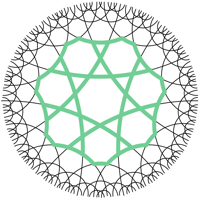
Hyperbolische KrŸmmung

NatŸrlich kšnnen wir ebenfalls Diagonalen einbauen. Das Siebeneck hat kurze und lange Diagonalen.

    

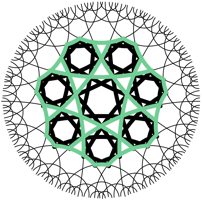
Kurze Diagonalen

    

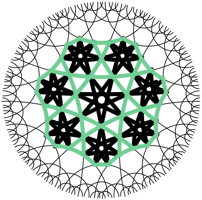
Lange Diagonalen

Die Diagonalen sind jeweils kŸrzer als die entsprechenden Diagonalen im ebenen Siebeneck.

Im ebenen Siebeneck ist:

 

 

 

 

Im Siebeneck unseres hyperbolischen Modells gilt:

 

 

 

 

Im hyperbolischen Modell sind die Diagonalen kŸrzer.

7     Von Sechsecken zu Siebenecken zu ... zu Zwšlfecken

Zwšlfeck

Literatur

Walser, Hans (2010): Handgreifliche Modelle der Kugelgeometrie und der hyperbolischen Geometrie. MU Der Mathematikunterricht. Elemente nichteuklidischer Geometrien. Jahrgang 56. Heft 6. Dezember 2010. Friedrich Verlag, Seelze. S. 28-37.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.

Walser, Hans (2017): EAGLE STARTHILFE Kartografie. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-95922-098-9.

Websites

 

[1] Hans Walser: ZahlenrŠtsel:

www.walser-h-m.ch/hans/Vortraege/20180208/Zahlenraetsel.pdf

 

[2] Hans Walser: Formeln fŸr die sphŠrische, euklidische und hyperbolische Geometrie:

http://www.walser-h-m.ch/hans/Miniaturen/F/Formeln/Formeln.htm

 

Last modified: 22. Dezember 2018