Hans Walser
Aufwickeln und Abwickeln

111. MNU-Bundeskongress 15.-18.04.2020 in Bingen
Zusammenfassung: Beispiele von wenig bekannten Abwicklungen. Diskussion zum Begriff ãNetzÒ. Minimale Anzahl Klebelaschen. Aufwickeln zu Kreis und Dreieck. Mechanische Modelle. Das Rad auf dem Rad und die Fourier-Entwicklung. Hundekurve und Parametertransformation. Winkeldrittelung. Konstruierbarkeit mit Zirkel und Lineal. Aufwickeln zum Würfel. Roboter mit fünf bewegten Drehachsen.
Letzte nderung: 16. Januar 2020
1 Wozu passen die Abwicklungen?
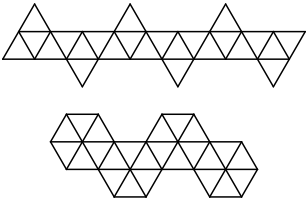
Zu welchen Krpern passen die Abwicklungen?
Beide Abwicklungen bestehen aus 24 Dreiecken. Das Ikosaeder kommt also nicht in Frage. Gehren die beiden Abwicklungen zum selben Krper? Beim unteren Beispiel ist irritierend, dass sechs Dreiecke an einer Ecke zusammenkommen. Ist das im nicht-ebenen Fall mglich?
Das obere Beispiel kann unterteilt werden in sechs Tetraederabwicklungen. Tatschlich knnen wir die Abwicklung sechslagig (Problem mit der Papierdicke) auf ein Tetraeder aufwickeln.
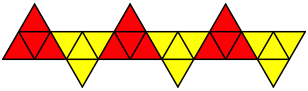
Sechsfache Tetraederabwicklung
Wir sehen darin aber auch eine dreifache Oktaederabwicklung.
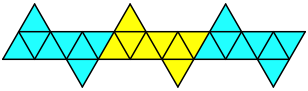
Dreifache Oktaederabwicklung
2 Abwicklungen des Wrfels
Die Wrfelabwicklungen sind uns vertraut.

Die elf Wrfelabwicklungen
In der Schule ist es blich, nach der Position der Klebelaschen zu fragen. Ein einfacher Trick besteht darin, an jeder zweiten Kante eine Klebelasche anzubringen (Rei§verschlusstechnik).
Wir knnen auch nach der Minimalzahl an Klebelaschen fragen, so dass das Wrfelmodell gerade noch stabil ist.
Das Experiment an realen Abwicklungen zeigt:
á Neun der elf Abwicklungen bentigen zwei Klebelaschen. In der folgenden Abbildung sind das die ersten neun Abwicklungen. Die Lsungen sind exemplarisch, es gibt noch andere. Kanten, die mit einer Klebelasche verbunden werden mssen, sind in gleicher Farbe angegeben. Bei zwei roten Kanten muss also an einer der beiden roten Kanten eine Klebelasche angebracht werden, die dann mit der anderen roten Kante verklebt werden kann. Analog fr zwei blaue Kanten.
á Die beiden letzten Abwicklungen kommen mit einer einzigen Klebelasche aus.
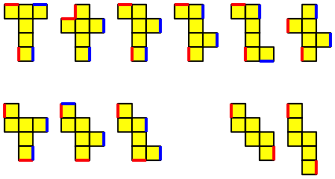
Lsung
Die beiden letzten Abwicklungen lassen sich je zu einem (unendlich langen) Bandornament fortsetzen.

Bandornamente
Ein solches Bandornament lsst sich (unendlich dnnes Material vorausgesetzt) (unendlich oft) auf einen gegebenen Wrfel aufwickeln, ohne dass abstehende Ohren entstehen. Wir knnen das Ornament als Getriebekette verwenden.


Kettengetriebe. Wrfel als Zahnrad
3 Netz?
In der Schule wird oft der Ausdruck ãWrfelnetzÒ verwendet. So steht es sogar im Lehrplan. Sinnvoll ist das nicht, denn in der Alltagssprache bedeutet ãNetzÒ meist ein System aus Knoten und Verbindungen.
Beispiele:
Sammelnetz:
Spinnennetz, Fischernetz, Einkaufsnetz, Gepcknetz, Haarnetz
Verteilnetz:
Versorgungsnetz, Verkehrsnetz, Stromnetz, Wassernetz, Gasnetz
Kommunikationsnetz:
Internet, Telefonnetz, soziales Netz
Koordinatennetz
Im folgenden Beispiel stimmt das System der Knoten und Verbindungen nicht mit der Realitt berein.

Welche Kanten fhren zum blauen Punkt?
Die folgenden sprachlich korrekten Wrfelnetze geben Auskunft ber die Topologie des Wrfels, sind aber keine Schnittmuster oder Abwicklungen.
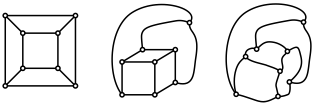
Wrfelnetze
4 Aufwickeln zum Kreis
4.1 Straffer Faden
Die Abbildung zeigt die verschiedenen Stadien des Aufwickelns.

Aufwickeln mit straff gespanntem Faden
Die Bahnkurve des Fadenendes ist eine Evolvente des Kreises.
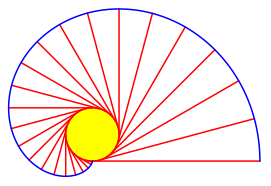
Evolvente
4.2 Lockerer Faden
Der Faden ist nun nicht mehr gespannt, sondern jeweils gleichm§ig gekrmmt, also ein Kreisbogen.

Gleichm§ig gekrmmt
Die Bahnkurve der Fadenenden ist eine Art halbe Herzkurve, aber nicht die offizielle Kardioide.

Halbe Herzkurve
5 Aufwickeln zum Dreieck
Wir arbeiten mit einem gleichm§ig geknickten Gelenkmodell. Die Au§enwinkel sind jeweils konstant.
![]()
Gleichm§ig geknicktes Gelenkmodell
Das Abknicken kann mit einem mechanischen Modell realisiert werden.

Mechanisches Modell
Die folgende Abbildung zeigt die verschiedenen Stadien des Aufwickelns.

Aufwickeln
Die Bahnkurven der Gelenke und Endpunkte sind Kreise und Kreisberlagerungen.
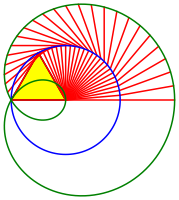
Bahnkurven
6 Kollision
Wir erkennen an der Dreiecksspitze, dass die Gelenkstbe diese teilweise berschneiden. Wo findet die Kollision statt?
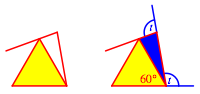
Kollision
Das blaue Dreieck ist gleichschenklig. Wir rechnen nun mit den Au§enwinkeln dieses Dreieckes. An der Basis haben wir je den Au§enwinkel t, an der Spitze den Au§enwinkel t + 60¡. Die Summe der drei Au§enwinkel ist 3t + 60¡. Andererseits ist bei einem Dreieck (allgemein bei einem Polygon mit der Umlaufszahl 1) die Summe der Au§enwinkel 360¡ (volle Richtungsnderung bei einem Umlauf). Damit erhalten wir:
3t + 60¡ = 360¡
t = 100¡
Das Resultat ist schn, aber ungewohnt. Ich habe bis anhin noch nie einen Winkel von 100¡ angetroffen.
7 Konstruktion mit Zirkel und Lineal
Ein Winkel von 100¡ kann nicht mit Zirkel und Lineal konstruiert werden. Falls nmlich ein Winkel von 100¡ mit Zirkel und Lineal konstruierbar wre, dann auch dein Winkel von 100¡ – 60¡ = 40¡. Das ist aber der Zentriwinkel eines regelm§igen Neuneckes, das mithin auch mit Zirkel und Lineal konstruierbar wre. Dies widerspricht aber einem Satz von Gau§ ber die Konstruierbarkeit regelm§iger Vielecke.
8 Aufwickeln zum Quadrat und zum Fnfeck
Beim Quadrat und beim regelm§igen Fnfeck gibt es ebenfalls Kollisionspunkte.
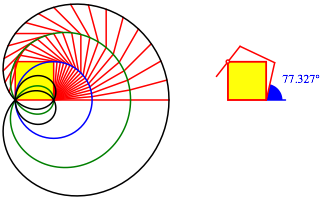
Aufwickeln zum Quadrat
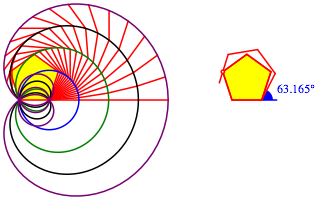
Aufwickeln zum Fnfeck
9 Aufwickeln zum Wrfel
Wir beginnen mit der ãschnenÒ Wrfelabwicklung.

ãSchneÒ Wrfelabwicklung
Im Folgenden einige Schritte des Aufwickelns. Wir beginnen in der Ebene.

Start in der Ebene
Nun drehen wir wie bei den Gelenkmodellen so, dass die Au§enwinkel bei aneinander sto§enden Quadraten immer gleich gro§ sind. Statt Gelenkpunkte haben wir nun Gelenkachsen, insgesamt fnf. Die folgende Abbildung zeigt die Situation nach Drehungen um 15¡.
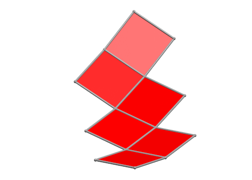
Drehungen um 15¡
Anschlie§end weitere Schritte.
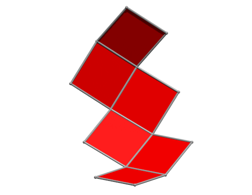
Drehungen um 30¡
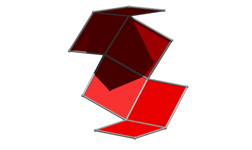
Drehungen um 45¡

Drehungen um 60¡

Drehungen um 75¡

Drehungen um 90¡
10 Weg auf der Oberflche
Wir zeichnen einen geraden (blauen) Weg auf der Abwicklung ein.
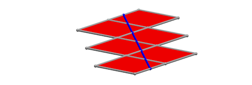
Blaue Gerade auf der Abwicklung
Durch das Drehen wird die blaue Gerade geknickt.
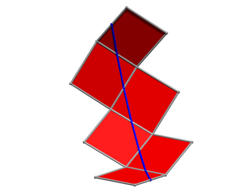
Drehungen um 30¡
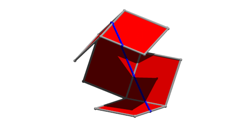
Drehungen um 60¡
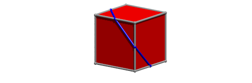
Drehungen um 90¡
Die blaue Gerade wird zu einem gleichm§ig geknickten Polygonzug. Wir vermuten, dass er immer in einer Ebene liegt. Dies drfte schon aus Symmetriegrnden klar sein, kann aber auch durch eine Plexiglasscheibe kontrolliert werden.
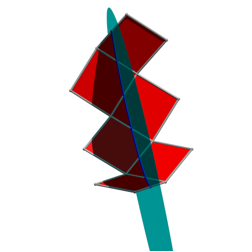
Drehungen um 30¡
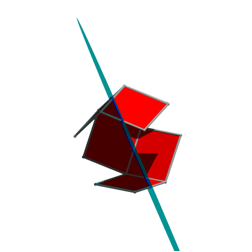
Drehungen um 60¡
Beim aufgewickelten Wrfel erhalten wir ein ebenes regelm§iges Sechseck.
11 Kollision mit dem Wrfel
Die Phnomene der Kollision und Durchdringung gibt es auch hier.
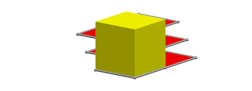
Aufwickeln zum Wrfel
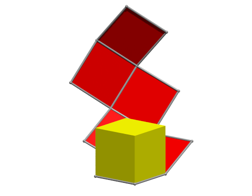
Drehungen um 30¡

Drehungen um 60¡

Drehungen um 70¡. Jetzt kommtÕs
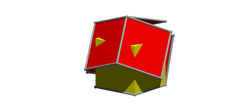
Drehungen um 75¡
12 Zurck zum Anfang: Wozu passen die Abwicklungen?
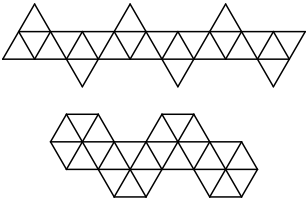
Zu welchen Krpern passen die Abwicklungen?
12.1 Kepler-Stern
Die obere Abwicklung passt zum Kepler-Stern.

Kepler-Stern
In der folgenden Abbildung sind Seitenflchen, welche in derselben Ebene liegen, mit derselben Farbe versehen.
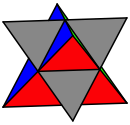
Ebenenkonsistente Frbung
Die folgende Abbildung zeigt die entsprechend gefrbte Abwicklung.

Zugehrige Abwicklung
12.2 Stern mit sechs Spitzen
Wenn wir auf jeder Seitenflche eines Wrfels eine Pyramide mit gleichseitigen Dreiecken als Seitenflche aufbauen, erhalten wir einen Stern mit sechs Spitzen. Dieser hat die Abwicklung der folgenden Figur.
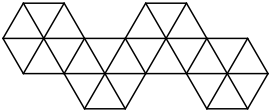
Abwicklung des Sterns mit sechs Spitzen

Stern mit sechs Spitzen
Literatur
Walser, Hans (2018): Der Wrfel. Ansichten – Dimensionen – Modelle. Edition am Gutenbergplatz, Leipzig 2018. ISBN 978-3-95922-102-3.
Weblinks
Hans Walser: Dreiecksaufwicklung
www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksaufwicklung/Dreiecksaufwicklung.htm
Hans Walser: Fahnenwrfel
http://www.walser-h-m.ch/hans/Miniaturen/F/Fahnenwuerfel/Fahnenwuerfel.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve/Herzkurve.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve2/Herzkurve2.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm
Hans Walser: Herzkurve und die Mndchen des Hippokrates
www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm
Hans Walser: Herzkurven
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurven/Herzkurven.htm
Hans Walser: Kepler-Stern und verwandter Stern
http://www.walser-h-m.ch/hans/Miniaturen/K/Kepler-Stern/Kepler-Stern.htm
Hans Walser: Klebelaschen
http://www.walser-h-m.ch/hans/Miniaturen/K/Klebelaschen/Klebelaschen.htm
Hans Walser: Klebelaschen 2
http://www.walser-h-m.ch/hans/Miniaturen/K/Klebelaschen2/Klebelaschen2.htm
Hans Walser: Netz
http://www.walser-h-m.ch/hans/Miniaturen/N/Netz/Netz.htm
Hans Walser: Wrfelabwicklungen
www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelabwicklungen/Wuerfelabwicklungen.htm