Hans Walser
Magische Symmetrie
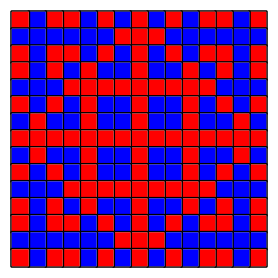
Graz, Tag der Mathematik
Do, 4.
Februar 2021
Bei der Analyse magischer Quadrate ungerader Seitenlnge treten verschiedene Symmetrien auf. Umgekehrt ist fr die Konstruktion magischer Quadrate ein symmetrisches modulo-Rechnen problemadquat. Ebenso brauchen wir ein angepasstes symmetrisches Positionssystem.
Zwei magische Quadrate ungerader Seitenlnge knnen zu einem neuen magischen Quadrat zusammengesetzt werden.
1 Beispiel – und ein Puzzle
Die Abbildung 1a zeigt ein magisches Quadrat der Seitenlnge 3. Die Zeilen-, Spalten- und Diagonalensummen sind je 15.
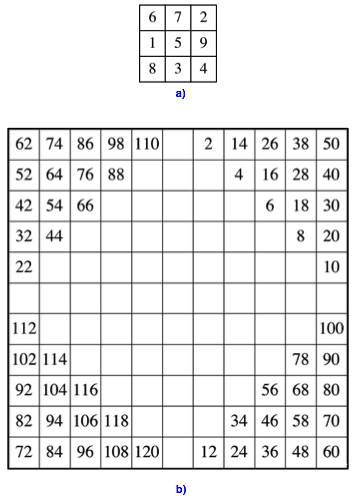
Abb. 1: Magische Quadrate der Seitenlngen 3 und 11
Im Quadrat der Abbildung 1b sind alle geraden Zahlen von 2 bis 120 eingetragen.
Frage 1: Wie kann das Quadrat der Abbildung 1b mit den ungeraden Zahlen von 1 bis 121 zu einem magischen Quadrat ergnzt werden?
2 Symmetrien
Die Abbildung 2a zeigt ein magisches Quadrat der Seitenlnge 5.
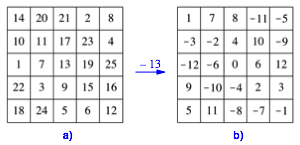
Abb. 2: Magische Quadrate der Seitenlnge 5
Frage 2: Welche Symmetrie-Eigenschaften hat das magische Quadrat der Abbildung 2a?
Im magischen Quadrat der Abbildung 2a subtrahieren wir 13 von jeder Zahl. Dadurch entsteht ein neues magisches Quadrat (Abb. 2b). Seine Zahlen laufen symmetrisch von –12 bis +12, mit der Null in der Mitte. Diese sitzt auch in der Mitte des Quadrates. Die Zeilen-, Spalten- und Diagonalensummen sind null. Entgegengesetzt positionierte Zahlen sind entgegengesetzt gleich.
Die
Abbildung 3 zeigt ein mit dem Faktor ![]() unterhht gezeichnetes
Histogramm des magischen Quadrates der Abbildung 2b. Die Figur ist
punktsymmetrisch.
unterhht gezeichnetes
Histogramm des magischen Quadrates der Abbildung 2b. Die Figur ist
punktsymmetrisch.
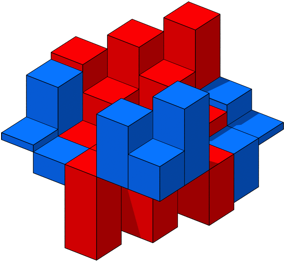
Abb. 3: Histogramm
3 Konstruktion eines magischen Quadrates
Wir besprechen zunchst die Konstruktion exemplarisch fr die Seitenlnge 5 und verallgemeinern anschlie§end.
In einem 5×5-Raster tragen wir in der Diagonale von links unten nach rechts oben Nullen ein, und zwar jeweils in der rechten Feldhlfte (Abb. 4a), damit es in der linken Feldhlfte noch Platz fr einen zweiten Eintrag hat.
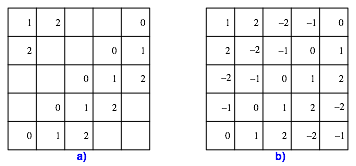
Abb. 4: Konstruktion, erster Schritt
In der anschlie§enden Nebendiagonale tragen wir Einsen ein. Dabei denken wir uns den rechten Bildrand mit dem linken identifiziert. Daher steht auch im ersten Feld links oben eine Eins. Analog tragen wir in der nchsten Nebendiagonale Zweien ein.
Nun kmen die Dreien an die Reihe. Statt dessen tragen wir Zahlen –2 ein (Abb. 4b). Die Begrndung ist folgende: die Zahlen 3 und –2 sind kongruent modulo 5. Aus Symmetriegrnden nehmen wir die Zahl –2, weil sie nher an der Null liegt als die Drei. Entsprechend tragen wir schlie§lich statt den Vieren die Zahlen –1 ein.
Im Feld der Abbildung 4b ist jede Zeilen- und jede Spaltensumme null, weil in jeder Zeile und in jeder Spalte genau die Zahlen –2, –1, 0, 1, 2 vorkommen. Dasselbe gilt auch fr die Diagonale von links oben nach rechts unten. In der Diagonale von links unten nach rechts oben haben wir gem§ Konstruktion lauter Nullen und daher die Summe null.
Symmetrisches
modulo-Rechnen: Die Abbildung 5a zeigt den Funktionsgrafen bei der blichen
Berechnung modulo 5 (nicht negativer Rest bei Division durch 5). Die Abbildung
5b zeigt die von uns verwendete Version (der Buchstabe ãsÒ deutet auf die symmetrische
Version hin). Der Funktionsgraf ist punktsymmetrisch zum Ursprung. Es ist exemplarisch
![]() , aber
, aber ![]() .
.
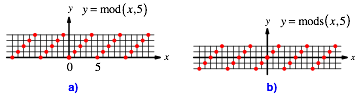
Abb. 5: modulo 5 – Verschiedene Reprsentanten
Frage 3: Wie kann mit Hilfe der
Funktion ![]() die
Funktion
die
Funktion ![]() konstruiert werden?
konstruiert werden?
Nun drehen wir die Zahlenanordnung der Abbildung 4b um den Mittelpunkt im Gegenuhrzeigersinn um 90¡ und setzen die gedrehten Zahlen vor die ursprnglichen. So erhalten wir Zahlenpaare gem§ Abbildung 6a.
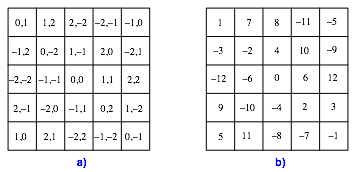
Abb. 6: Zahlenpaare und Linearkombination
In der
Abbildung 6a sind sowohl fr die ersten Zahlen wie auch fr die zweiten Zahlen
die Zeilen-, Spalten- und Diagonalensummen null. Das gibt auch fr jede
Linearkombination der beiden Zahlenanordnungen. Wir whlen die folgende
Linearkombination: zum Fnffachen (fnf ist die Seitenlnge des Quadrates) der
ersten Zahlen addieren wir die zweiten Zahlen. So erhalten wir etwa aus dem
Zahlenpaar ![]() die neue
Zahl
die neue
Zahl ![]() . Wir interpretieren also das Zahlenpaar als
zweistellige Zahl im Positionssystem mit der Basis 5. Dabei knnen allerdings
die Anzahlen der Einer wie auch die Anzahlen der Fnfer negativ sein.
. Wir interpretieren also das Zahlenpaar als
zweistellige Zahl im Positionssystem mit der Basis 5. Dabei knnen allerdings
die Anzahlen der Einer wie auch die Anzahlen der Fnfer negativ sein.
Aus den Zahlenpaaren der Abbildung 6a ergibt sich so das magische Quadrat der Abbildung 6b mit den Summen null. Das ist aber unser magisches Quadrat der Abbildung 2b. Wenn wir jetzt noch 13 addieren, ergibt sich das magische Quadrat mit den Zahlen von 1 bis 25 (Abb. 2a).
4 Verallgemeinerung
Wir
konstruieren ein magisches Quadrat der ungeraden Seitenlnge ![]() .
.
Die
bliche Indizierung der Elemente ![]() einer
quadratischen Matrix beginnt links oben mit
einer
quadratischen Matrix beginnt links oben mit ![]() und endet
rechts unten mit
und endet
rechts unten mit ![]() . Das ist fr uns unpassend. Wir verwenden statt
dessen eine bezglich null symmetrische Indizierung gem§ Abbildung 7a. Das
Element
. Das ist fr uns unpassend. Wir verwenden statt
dessen eine bezglich null symmetrische Indizierung gem§ Abbildung 7a. Das
Element ![]() sitzt in
der Mitte. Links oben haben wir das Element
sitzt in
der Mitte. Links oben haben wir das Element ![]() , rechts unten das Element
, rechts unten das Element ![]() .
.
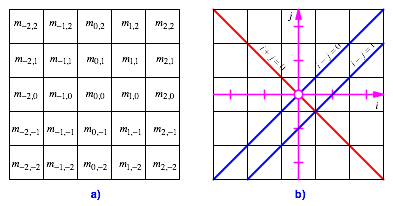
Abb. 7: Indizierung und Koordinatensystem
Dazu
passend fhren wir ein ![]() -Koordinatensystem ein gem§ Abbildung 7b. Die
Diagonale von links unten nach rechts oben hat darin die Gleichung
-Koordinatensystem ein gem§ Abbildung 7b. Die
Diagonale von links unten nach rechts oben hat darin die Gleichung ![]() , die dazu parallelen Nebendiagonalen die Gleichung
, die dazu parallelen Nebendiagonalen die Gleichung ![]() . Die Diagonale von links oben nach rechts unten hat
die Gleichung
. Die Diagonale von links oben nach rechts unten hat
die Gleichung ![]() , die dazu parallelen Nebendiagonalen die Gleichung
, die dazu parallelen Nebendiagonalen die Gleichung ![]() .
.
In dieser
Schreibweise erhalten wir fr ![]() gem§
unserer Konstruktion die Formel:
gem§
unserer Konstruktion die Formel:
![]()
Entsprechend gilt allgemein:
![]()
Bei
dieser Formel haben wir die Null in der Mitte, und die Zahlen laufen von ![]() bis
bis ![]() . Wenn die Zahlen von 1 bis
. Wenn die Zahlen von 1 bis ![]() laufen
sollen, mssen wir noch
laufen
sollen, mssen wir noch ![]() addieren.
addieren.
Frage 4: Gesucht ist ein magisches Quadrat mit den Zahlen von 1 bis 49.
5 Ganze Zahlen ohne Minuszeichen
Wir hatten oben in einem Positionssystem mit der Basis 5 gearbeitet, aber auch negative Anzahlen der Einer oder der Fnfer zugelassen. Dies fhrt zur Idee eines Positionssystems, in welchem die negativen ganzen Zahlen ohne sichtbares Minuszeichen darstellt werden knnen.
Wir legen fnf Symbole fr die einzelnen Ziffern fest. Um keine Verwirrung mit dem blichen Positionssystem zu schaffen, verwenden wir Buchstaben in folgender Bedeutung:
|
Ziffernsymbol |
a |
b |
c |
d |
e |
|
Bedeutung |
–2 |
1 |
0 |
1 |
2 |
Wir sehen, dass der Hund (die Minuszeichen) in den Symbolen begraben ist.
Zunchst zwei Beispiele.
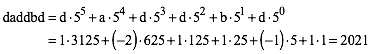
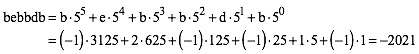
Wir knnen also die Zahl –2021 ohne sichtbares Minuszeichen darstellen.
Frage 5: Wie lautet ãdadÒ im Dezimalsystem?
Frage 6: Wie lautet ãbabbeÒ im Dezimalsystem?
Frage 7: Wie sieht die Dezimalzahl –753 in diesem System aus?
Nun rechnen wir die Zahlen des magischen Quadrates der Abbildungen 2b oder 6b in unser vorzeichenfreies System um (Abb. 8).
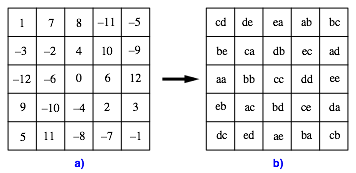
Abb. 8: Umrechnung
Es kommen in jeder Zeile und in jeder Spalte alle fnf Buchstaben sowohl vorne wie auch hinten genau einmal vor. Weiter kommt jede der 25 Paar-Kombinationen der fnf Buchstaben genau einmal vor.
Solche paarweise Anordnungen von Buchstaben wurden von Leonhard Euler (1707-1783) in [1] untersucht.
6 Zusammensetzung zweier magischer Quadrate
Mit zwei
magischen Quadraten der Seitenlngen ![]() und
und ![]() knnen wir
ein magisches Quadrat der Seitenlnge
knnen wir
ein magisches Quadrat der Seitenlnge ![]() konstruieren. Wir zeigen dies
exemplarisch mit den beiden magischen Quadraten der Abbildung 9. Diese haben
die Seitenlngen 3 beziehungsweise 5. Ihre Zahlen laufen von 0 bis 8
beziehungsweise von 0 bis 24.
konstruieren. Wir zeigen dies
exemplarisch mit den beiden magischen Quadraten der Abbildung 9. Diese haben
die Seitenlngen 3 beziehungsweise 5. Ihre Zahlen laufen von 0 bis 8
beziehungsweise von 0 bis 24.
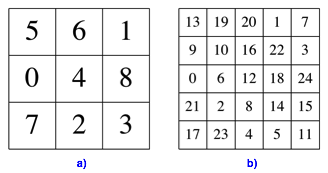
Abb. 9: Die beiden magischen Quadrate
In der Abbildung 10 sind die Felder der geraden Zahlen rot, die Felder der ungeraden Zahlen blau eingefrbt.
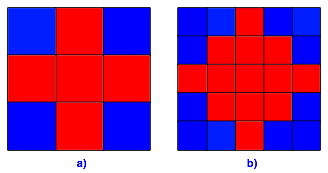
Abb. 10: Parittische Frbung
Die Abbildung 11 zeigt die zugehrigen Histogramme.
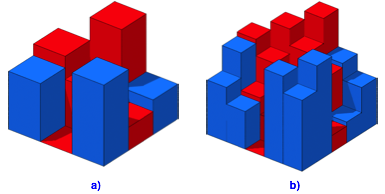
Abb. 11: Histogramme
Und nun machen wir folgendes: wir vergr§ern das Histogramm der Abbildung 11a in den beiden horizontalen Dimensionen je mit dem Faktor 5 und in der vertikalen Richtung sogar mit dem Faktor 25. Damit erhalten wir die Figur der Abbildung 12a. Da sie, wie alle Histogramme in diesem Skript unterhht gezeichnet ist, fllt die gro§e Streckung in vertikaler Richtung nicht ins Auge.
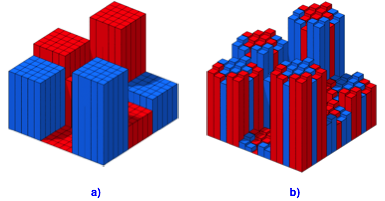
Abb. 12: Plattformen und Besiedlung der Plattformen
Wir erkennen in der Abbildung 12a neun 5×5-Plattformen. Wir knnen auf jeder dieser Plattformen ein Histogramm der Abbildung 11b setzen und erhalten damit das Histogramm der Abbildung 12b.
Die Abbildung 13 zeigt das zugehrige magische Quadrat. Seine Zahlen laufen von 0 bis 224.
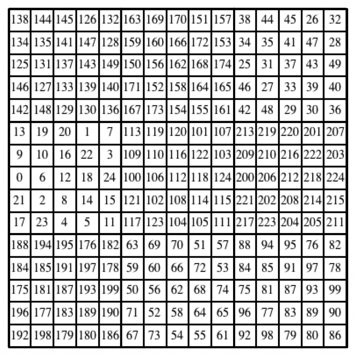
Abb. 13: Magisches Quadrat der Seitenlnge 15
Wir sehen am linken Rand in der Mitte das magische 5×5-Quadrat der Abbildung 9b. Es sitzt auf der Null des magischen 3×3-Quadrates der Abbildung 9a.
Die Abbildung 14 zeigt die parittische Frbung.

Abb. 14: Parittische Frbung
Frage 8: Liefern die Formeln im Abschnitt 4 fr ![]() dasselbe magische
Quadrat wie in der Abbildung 13?
dasselbe magische
Quadrat wie in der Abbildung 13?
Frage 9: Knnen wir bei der Zusammensetzung die Reihenfolge der beiden magischen Quadrate vertauschen?
7 Bearbeitung der Fragen
Bearbeitung der Frage 1: Die Abbildung 15a zeigt das vollstndige magische Quadrat.
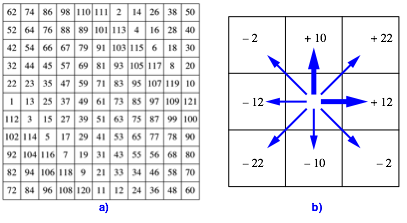
Abb. 15: Magisches Quadrat der Seitenlnge 11. Vernderungen
Die Abbildung 15b illustriert, wie sich innerhalb des Bereiches der geraden Zahlen wie auch innerhalb des Bereiches der ungeraden Zahlen die Zahlen beim bergang zu einem Nachbarfeld verndern. Dabei enthalten die Vernderungen entlang der fett eingezeichneten Pfeile die gesamte Information. Diese Vernderungen sind um eins gr§er beziehungsweise um eins kleiner als die Seitenlnge des magischen Quadrates.
Die brigen Vernderungen ergeben sich durch lineare Kombination.
An der Grenze zwischen den geraden und den ungeraden Zahlen gelten andere Vernderungsregeln.
In der Abbildung 16 sind die Felder des magischen Quadrates mit geraden Zahlen rot, die Felder mit ungeraden Zahlen blau eingefrbt. Die Zahlen selber sind weggelassen.
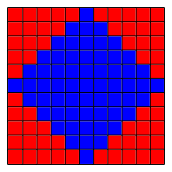
Abb. 16: Parittische Frbung
Bearbeitung der Frage 2: Die Zahlen laufen von 1 bis 25, der Median ist 13. Diese Zahl sitzt auch in der Mitte des Quadrates, ist also ein ãMedianÒ in doppeltem Sinn.
Die Zeilen-, Spalten- und Diagonalensummen sind je 65. Dies ist das Fnffache des Medians in der Mitte. Hier spielt die Seitenlnge des magischen Quadrates hinein.
Zwei Zahlen, die bezglich des Medians in der Mitte punktsymmetrisch angeordnet sind (zum Beispiel die Zahlen 4 und 22) haben das arithmetische Mittel 13. Schon wieder die 13.
Die Felder der ungeraden Zahlen bilden ein auf der Spitze stehendes Quadrat (blau in Abb. 17).
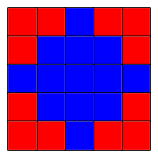
Abb. 17: Parittische Frbung
Die
Abbildung 18 zeigt das zu diesem magischen Quadrat gehrende Histogramm. Es ist
in der Hhe mit dem Faktor ![]() gestaucht.
gestaucht.
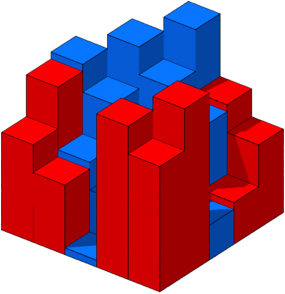
Abb. 18: Histogramm
Bearbeitung der Frage 3: Es ist:
![]()
Bearbeitung der Frage 4: Das magische Quadrat hat die Seitenlnge 7 (Abb. 19).
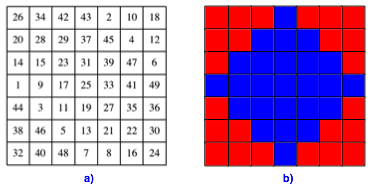
Abb. 19: Magisches Quadrat der Seitenlnge 7. Parittische Frbung
Bearbeitung der Frage 5:
![]()
Bearbeitung der Frage 6:
![]()
Bearbeitung der Frage 7:
![]()
Bearbeitung der Frage 8: Nein. Die Abbildung 20a zeigt das entsprechende Histogramm. Es unterscheidet sich deutlich vom Histogramm der Abbildung 12b. Auch die Frbung (Abb. 20b) unterscheidet sich von derjenigen der Abbildung 14.
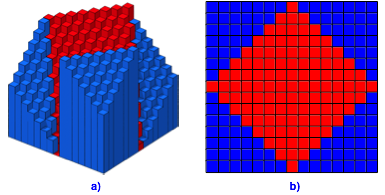
Abb. 20: Histogramm. Parittische Frbung
Bearbeitung der Frage 9: Nochmals nein. Die Abbildung 21a zeigt das entsprechende Histogramm. Es unterscheidet sich deutlich vom Histogramm der Abbildung 12b. Auch die Frbung (Abb. 21b) unterscheidet sich von derjenigen der Abbildung 14.
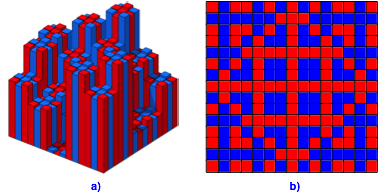
Abb. 21: Histogramm. Parittische Frbung
Die Zusammensetzung der magischen Quadrate ist nicht kommutativ.
Last modified: 29. Januar 2021
Literatur
|
Euler, Leonhard |
[1] |
Recherches sur une nouvelle espce de quarrs magiques, Vlissingen 1782 – Opera Omnia, Series 1, Volume 7, p. 291-392. Enestrm Index 530. |
Websites
Hans Walser: Magische Kreise
www.walser-h-m.ch/hans/Miniaturen/M/Magische_Kreise/Magische_Kreise.htm
Hans Walser: Magische Quadrate quadrieren
www.walser-h-m.ch/hans/Miniaturen/M/Mag_Quadrate2/Mag_Quadrate2.htm
Hans Walser: Magische Quadrate berlagern
www.walser-h-m.ch/hans/Miniaturen/M/Mag_Quadrate4/Mag_Quadrate4.htm
Hans Walser: Magische Quadrate ungerader Seitenlnge
www.walser-h-m.ch/hans/Miniaturen/M/Mag_Quadrate/Mag_Quadrate.htm
Hans Walser: Magische Puzzle
www.walser-h-m.ch/hans/Miniaturen/M/Mag_Puzzle/Mag_Puzzle.htm
Hans Walser: Magisches Fraktal
www.walser-h-m.ch/hans/Miniaturen/M/Magisches_Fraktal/Magisches_Fraktal.htm
Vortragsunterlagen
Hans Walser: Magische Symmetrie
http://www.walser-h-m.ch/hans/Vortraege/20210204/index.html