Hans Walser

Halbe Würfel

Tag der Mathematik

Freitag, 8. April 2022

Bozen

Inhalt

1 Worum geht es?.......................................................................................................... 2

2 Würfelhalbierung........................................................................................................ 2

2.1 Beispiele.............................................................................................................. 2

2.2 Der Affensattel..................................................................................................... 3

2.3 Zwölffüßler.......................................................................................................... 4

3 Raumfüller.................................................................................................................. 5

4 Exkurs: Vier Farben.................................................................................................... 6

5 Ein kantiger Affensattel und ein Stern....................................................................... 6

6 Ein Kreuz und das Komplement dazu........................................................................ 7

6.1 Das Kreuz............................................................................................................ 7

6.2 Komplement........................................................................................................ 8

6.3 Exkurs: Eine Variante zum Menger-Schwamm.................................................. 9

7 Statisches Passen und kinematisches Einpassen...................................................... 10

7.1 Puzzle................................................................................................................. 10

7.2 Knacknuss ohne Nussknacker........................................................................... 11

8 Origami in der Ebene................................................................................................ 12

9 Räumliches Origami................................................................................................. 14

9.1 Einfalten der Seitenmitten................................................................................. 14

9.2 Einfalten der Kantenmitten................................................................................ 15

9.3 Einfalten der Ecken........................................................................................... 17

1 Worum geht es?

Ein Würfel kann nicht mit Zirkel und Lineal in einen volumenmäßig halb so großen Würfel verwandelt werden. Hingegen gibt es eine Vielzahl von einfach zu konstruierenden Figuren, welche das Würfelvolumen halbieren. Dabei spielen Symmetrieüberlegungen eine wichtige Rolle. Mit diesen Figuren kann der Raum lückenlos und überlappungsfrei aufgefüllt werden. Dabei zeigt sich der Unterschied zwischen dem statischen „Passen“ und dem kinematischen „Einpassen“. Die Überlegungen spielen in den Dimensionen zwei, drei und vier.

Für die Herstellung der Figuren wird unter anderem der „Affensattel“ verwendet. Weiter arbeiten wir virtuell mit 3d-Origami.

2 Würfelhalbierung

2.1 Beispiele

Beim Stichwort „Würfelhalbierung“ denken wir zunächst an das Problem, zu einem gegebenen Würfel einen volumenmäßig halb so großen Würfel zu finden. Dieses Problem – es handelt sich um das Pendant zur „Würfelverdoppelung“ – kann nicht mit Zirkel und Lineal gelöst werden. Hingegen können sehr einfach Figuren mit dem halben Würfelvolumen gefunden werden, welche selber keine Würfel sind (Abb. 1). Zu dieser Art der Würfelhalbierung siehe Walser (2018), S. 93-108.

Abb. 1: Halbes Würfelvolumen

Im zweiten und vierten Beispiel der Abbildung 1 sind der untere rote Teil und der obere weiße Ergänzungsteil ungleichsinnig kongruent.

2.2 Der Affensattel

Die Abbildung 2 zeigt den sogenannten Affensattel sowie einen auf eine Ecke gestellten Würfel.

Abb. 2: Affensattel und Würfel

Der Affensattel mit der Gleichung hat bezüglich der z-Achse eine dreiteilige Drehsymmetrie. Dies gilt aber auch für den Würfel, wenn eine Körperdiagonale auf der z-Achse liegt.

Wir schneiden nun mit Hilfe des Affensattels den oberen Teil des Würfels weg (Abb. 3). Somit erhalten wir einen halben Würfel. Das blau eingezeichnete Gegenstück liegt dazu punktsymmetrisch.

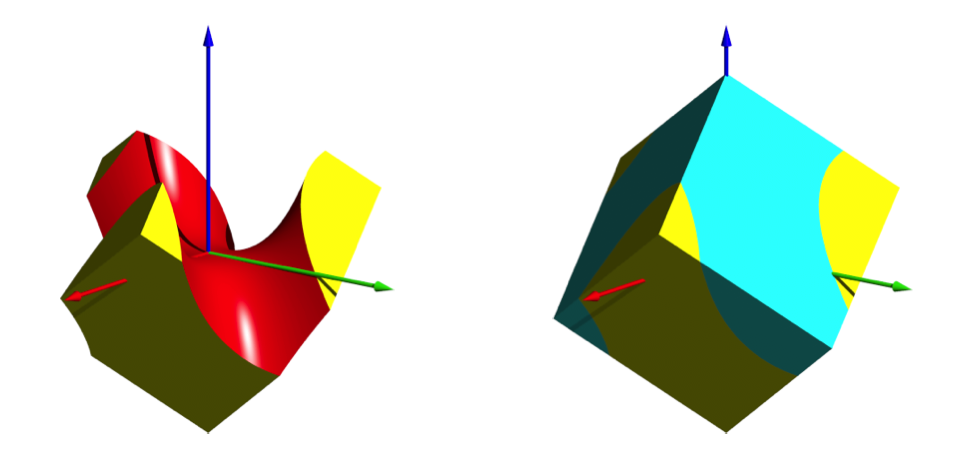
Abb. 3: Schnitt des Würfels mit dem Affensattel

Der Affensattel kann als Graf einer Funktion in x und y mit Funktionswerten in der z-Richtung gesehen werden. Daher schneidet jede Parallel zur z-Achse den Affensattel genau einmal. Wir können also die beiden halben Würfel der Abbildung 3 in der z-Richtung friktionslos auseinanderheben und kollisionsfrei wieder zusammenfügen (Abb. 4).

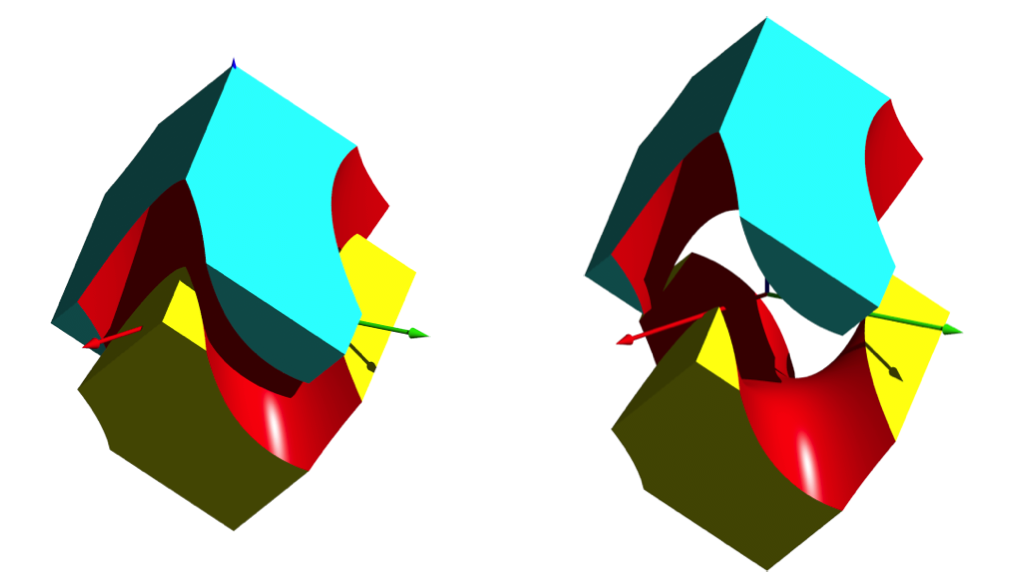
Abb. 4: Bewegen der beiden halben Würfel

2.3 Zwölffüßler

Wir legen nun einen der beiden halben Würfel so ins kartesische Koordinatensystem dass eine Ecke auf den Ursprung zu liegen kommt und drei Würfelkanten auf die Koordinatenachsen (Abb. 5).

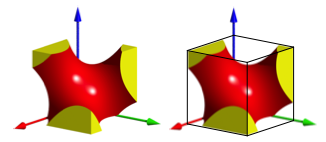
Abb. 5: Einpassen ins kartesische Koordinatensystem

Anschließend spiegeln wir die Figur an den Koordinatenebenen und erhalten so einen Zwölffüßler oder Dodekapus (Abb. 6).

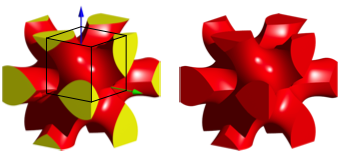
Abb. 6: Spiegelung an den Koordinatenebenen. Zwölffüßler

3 Raumfüller

Der Zwölffüßler ist ein sogenannter Raumfüller. Wir können mit kongruenten Zwölffüßlern den Raum lückenlos und durchdringungsfrei ausfüllen. Allerdings muss man dabei richtig vorgehen.

Der Versuch, zunächst vier Zwölffüßler in einer Ebene quadratisch auszulegen (Abb. 7, linkes Bild) und dann von oben einen fünften in die Lücke zu schieben, scheitert. Der blaue Zwölffüßler kollidiert mit den anderen.

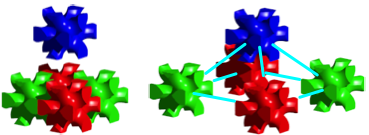
Abb. 7: Falsches und richtiges Vorgehen für das Einpassen

Wir müssen vielmehr die fünf Zwölffüßler zunächst räumlich so positionieren, dass ihre Mittelpunkte eine quadratische gerade Pyramide bilden, deren Höhe halb so lang ist wie die Grundkante (Abb. 7, rechtes Bild). Die Schrägkanten haben dann die Richtung der Würfeldiagonalen, längs derer das Zusammenschieben wie in der Abbildung 4 kollisionsfrei möglich ist. Das Zusammenschieben der fünf Zwölffüßler erfolgt dann durch simultanes Einpassen. Dazu sind fünf Hände erforderlich. Die Abbildung 8 zeigt das Ergebnis sowie eine größere Version.

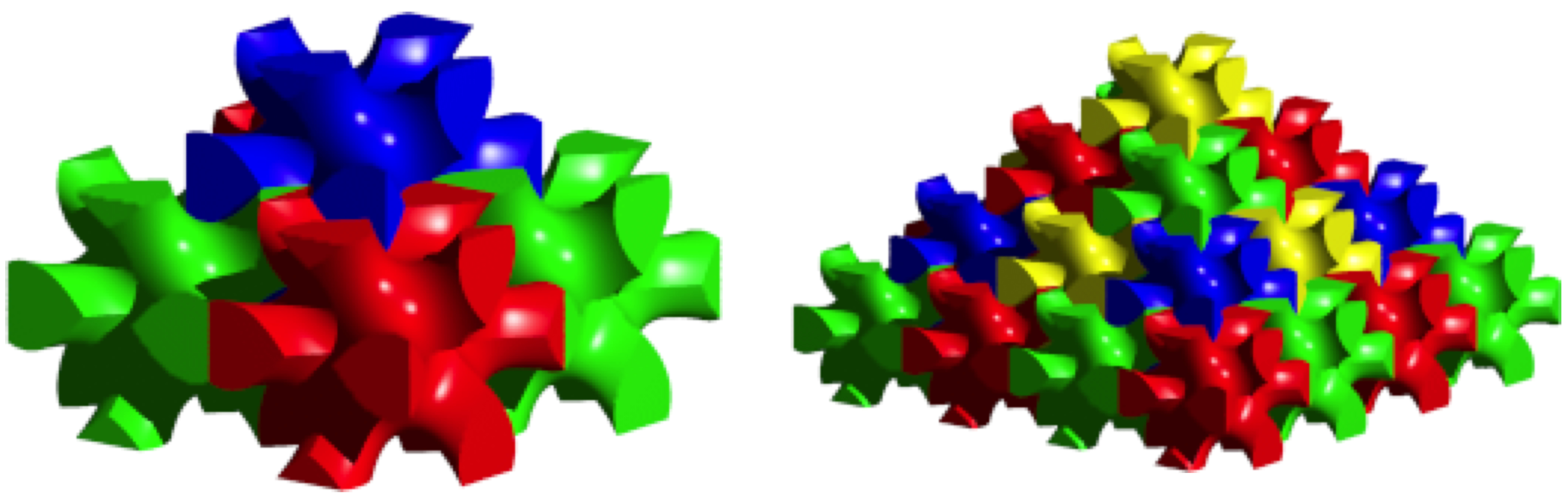
Abb. 8: Pyramiden aus Zwölffüßlern

4 Exkurs: Vier Farben

Bei der raumfüllenden pyramidalen Packung der Abbildung 8 kommen wir mit vier Farben aus, so dass nirgends zwei benachbarte gleichfarbige Zwölffüßler eine ebene oder gekrümmte Seitenfläche gemeinsam haben. Hingegen können sehr wohl gleichfarbige Zwölffüßler eine Kante oder eine Ecke gemeinsam haben. Diese Vierfarbeneigenschaft ist nicht trivial, da der ebene Vierfarbensatz im Raum nicht gilt.

Im Beispiel der Abbildung 8 ist die Pyramide aus horizontalen Schichten aufgebaut, welche alternierend ein rot-grünes oder ein blau-gelbes Schachbrettmuster bilden. Zudem sind zum Beispiel zwei aufeinanderfolgende rot-grüne Schichten farbversetzt. Daher können sich nirgends zwei gleiche Farben berühren.

Die Vierfarbeneigenschaft gilt analog für alle in diesem Beitrag vorkommenden Raumpackungen.

5 Ein kantiger Affensattel und ein Stern

Die Abbildung 9 zeigt eine Würfelhalbierung durch einen „kantigen“ Affensattel.

Abb. 9: Kantiger Affensattel

Die Konstruktion ist folgende. Wir können einen Würfel vom Mittelpunkt aus in sechs Pyramiden aufteilen, welche je eine Seitenfläche des Würfels als Grundfläche haben und die Würfelmitte als Spitze. In der Abbildung 9 sind drei der sechs Pyramiden so eingefügt, dass jede mit den beiden anderen je ein Seitendreieck gemeinsam hat. Die Figur hat eine dreiteilige Drehsymmetrie bezüglich der blau eingezeichneten Würfeldiagonale. Der Flächenwinkel an den Kanten des Affensattels ist 120°.

Durch Spiegeln erhalten wir einen Stern mit zwölf Spitzen (Abb. 10). Er ist wiederum ein halber Würfel.

Abb. 10: Stern

Dieser Stern ist ein Raumfüller (Abb. 11). Das Zusammenschieben ist problemlos möglich. Wir sehen wieder die Struktur mit den vier Farben.

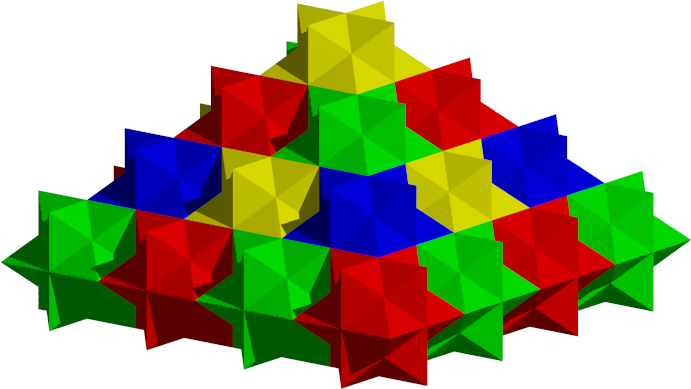
Abb. 11: Sternpyramide

6 Ein Kreuz und das Komplement dazu

6.1 Das Kreuz

Die Abbildung 12 zeigt zunächst einen Affensattel mit rechtwinkligen Kanten. Durch Spiegeln erhalten wir ein 3d-Kreuz. Auch dieses Kreuz kann als halber Würfel gesehen werden.

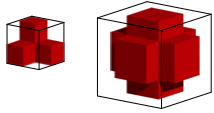
Abb. 12: Halber Würfel und Kreuz

Das 3d-Kreuz ist ein Raumfüller (Abb. 13). Das Zusammenschieben der einzelnen Kreuze ist problemlos möglich.

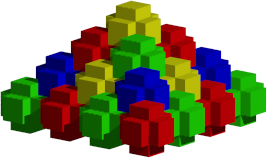
Abb. 13: Pyramide aus Kreuzen

6.2 Komplement

Nun drehen wir den Sattel der Abbildung 12 um, so dass wir ihn von hinten sehen (Abb. 14). Durch Spiegeln erhalten wir eine Figur, welche das Kreuz der Abbildung 12 zum Würfel ergänzt.

Abb. 14: Komplementäre Situation

Diese Figur ist ebenfalls ein Raumfüller (Abb. 15). Sie füllt den Raum im Innern der Pyramide lückenlos und durchdringungsfrei aus. Allerdings sind die einzelnen Bauteile völlig verkettet. Es ist nicht möglich, aus einzelnen losen Bauteilen die Pyramide zu bauen, ohne die Teile aufzureißen. Die Teile passen zwar ineinander, lassen sich aber nicht einpassen.

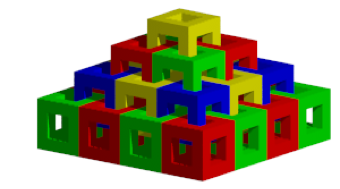
Abb. 15: Passt. Lässt sich aber nicht einpassen.

6.3 Exkurs: Eine Variante zum Menger-Schwamm

Die Figur der Abbildung 14 führt zu einer Variante des Menger-Schwamms. Die Abbildung 16 zeigt die ersten beiden Fraktalisierungsschritte.

Abb. 16: Variante zum Menger-Schwamm

Diese Variante hat im Unterschied zum originalen Mengerschwamm eine rationale fraktale Dimension, nämlich:

7 Statisches Passen und kinematisches Einpassen

In der Abbildung 15 sahen wir den Unterschied zwischen dem statischen Passen und dem kinematischen Einpassen. Im Folgenden weitere Beispiele.

7.1 Puzzle

Das Puzzle der Abbildung 17 ist beinahe fertig. Das fehlende Element rechts oben können wir aber nicht in der Ebene des Puzzles einpassen. Wir müssen es abheben und von oben her einpassen. Wir benötigen den Raum.

Abb. 17: Noch die Ecke einpassen

Im Beispiel der Abbildung 18 passt das Eckteil zwar in die Lücke, lässt sich aber nicht hineinschieben.

Abb. 18: Passt die Ecke in die Lücke?

Im vierdimensionalen Raum ließe sich das Problem sehr einfach lösen. Wir könnten die dreidimensionale Ecke in die vierte Dimension abheben und dann hineinschieben.

7.2 Knacknuss ohne Nussknacker

Die Abbildung 19 zeigt drei Nüsse je in zwei Ansichten. Das erste Beispiel ist eine übliche Nuss mit einer zweiteiligen Drehsymmetrie. Im zweiten Beispiel haben wir eine dreiteilige und im dritten Beispiel gar eine vierteilige Drehsymmetrie. Um Herauszufinden, ob die Kerne ebenfalls entsprechende Drehsymmetrien aufweisen, müssten die Nüsse geknackt werden. Das wäre aber schade um die seltenen Nüsse.

Abb. 19: Nüsse

Im vierdimensionalen Raum ließe sich das Problem sehr einfach lösen. Wir könnten den Kern einfach in die vierte Dimension herausheben. Die Abbildung 22 illustriert die Situation eine Dimension tiefer. Zweidimensionale Nusskerne erhalten wir durch Herausheben aus der zweidimensionalen Schale.

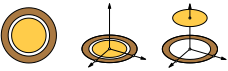
Abb. 20: Einbetten der 2d-Nuss in den Raum

8 Origami in der Ebene

Im Folgenden einige Beispiele für Faltprozesse mit dem üblichen zweidimensionalen Origami-Papier.

Die Abbildung 21 zeigt einen Origami-Würfel, der aus sechs Bauteilen besteht.

Abb. 21: Origami-Würfel. Bauteil

Die Abbildung 22 zeigt als einfachen Faltprozess, wie die Ecke links oben auf die Ecke rechts unten gefaltet wird. Wir nehmen an, das Papier sei auf einer Seite gelb und auf der anderen hellblau. Aus einem Quadrat erhalten wir ein zweilagiges halbes Quadrat.

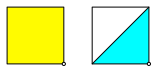
Abb. 22: Ecke links oben auf die Ecke rechts unten

Ein weiterer einfacher Faltprozess besteht darin, sukzessive die Kantenmitten oder die Ecken in die Quadratmitte einzufalten (Abb. 23). In beiden Fällen entsteht ein Quadrat.

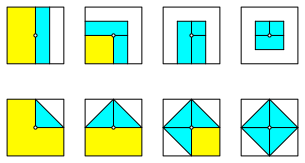
Abb. 23: Einfalten in die Quadratmitte

Wir übertragen diese Faltprozesse auf ein virtuelles 3d-Origami.

9 Räumliches Origami

Wie ist ein 3d-Origami zu verstehen? Dazu denken wir uns als Spielmaterial einen Würfel, den wir im vierdimensionalen Raum falten. Das Material für diesen Würfel muss noch erfunden werden. In der Abbildung 24 wird die Ecke links oben auf die diametrale Ecke rechts unten gefaltet.

Abb. 24: 3d-Origami

Natürlich kann dieser Faltprozess auch rein dreidimensional beschrieben werden. Wir halbieren den Würfel mit der Mittelnormalebene einer Körperdiagonalen und spiegeln die eine Hälfte auf die andere Seite.

9.1 Einfalten der Seitenmitten

Durch das Einfalten der Seitenflächenmitten auf den Würfelmittelpunkt erhalten wir nach sechs Schritten einen kleineren Würfel (Abb. 25). Er hat gegenüber dem Ausgangswürfel halbe Kantenlänge und damit einen Achtel des Volumens. Dafür hat er die achtfache Materialdichte. Natürlich ist dieser Würfel ein Raumfüller.

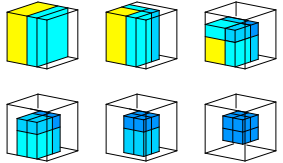
Abb. 25: Einfalten der Seitenflächenmitten in den Würfelmittelpunkt

9.2 Einfalten der Kantenmitten

Beim Einfalten der Kantenmitten in den Würfelmittelpunkt benötigen wir insgesamt zwölf Faltschritte. Nach den ersten vier Schritten ergibt sich ein Haus mit quadratischem Grundriss und einem Pyramidendach (Abb. 26).

Abb. 26: Einfalten der Kantenmitten in den Würfelmittelpunkt.

Nach weiteren vier Schritten erhalten wir wiederum ein Gebäude mit quadratischem Grundriss. Es hat ein Rhombendach (Abb. 27).

Abb. 27: Was geschieht zwischen dem zweiten und dem dritten Bild?

Solche Rhombendächer wurden als Turmhelme bei romanischen und neoromanischen Kirchen gebaut (Abb. 28).

Abb. 28: Kirche Krefeld

Die letzten vier Faltschritte schließlich führen zum Rhombendodekaeder (Abb. 29). Das Volumen des Rhombendodekaeders ist ein Viertel des ursprünglichen Würfelvolumens.

Abb. 29: Rhombendodekaeder

Das Rhombendodekaeder ist ebenfalls ein Raumfüller. In der Abbildung 30 ist eine Kugel durch eine Rhombendodekaeder-Packung approximiert.

Abb. 30: Rhombendodekaeder approximieren eine Kugel

9.3 Einfalten der Ecken

Durch Einfalten der Würfelecken in die Würfelmitte ergibt sich ein abgestumpftes Oktaeder (Abb. 31). Sein Volumen ist die Hälfte des Würfelvolumens. Der „Affensattel“ ist jetzt ein Hocker mit einem ebenen regelmäßigen Sechseck als Sitzfläche.

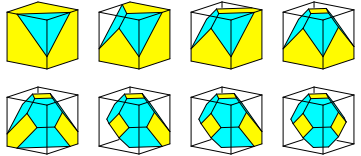
Abb. 31: Einfalten der Ecken in die Würfelmitte

Das abgestumpfte Oktaeder ist ebenfalls ein Raumfüller (Abb. 32).

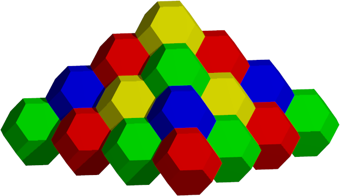
Abb. 32: Pyramide aus abgestumpften Oktaedern

Literatur

Walser, Hans (2018): Der Würfel. Ansichten – Dimensionen – Modelle. Edition am Gutenbergplatz, Leipzig 2018. ISBN 978-3-95922-102-3.