Aufwickeln und Abwickeln

Hans Walser

Zusammenfassung: Beispiele von wenig bekannten Abwicklungen. Diskussion zum Begriff „Netz“. Minimale Anzahl Klebelaschen. Aufwickeln zu Kreis und Dreieck. Mechanische Modelle. Das Rad auf dem Rad und die Fourier-Entwicklung. Hundekurve und Parametertransformation. Winkeldrittelung. Konstruierbarkeit mit Zirkel und Lineal. Aufwickeln zum Würfel. Roboter mit fünf bewegten Drehachsen.

Aufwickel-Beweis des Satzes des Pythagoras

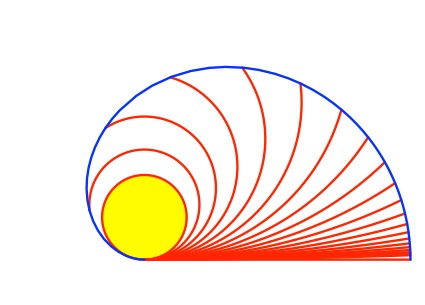
Die Abbildung 0 zeigt Szenen aus einem Auf- und Abwickel-Beweis für den Satz des Pythagoras.

Abb. 0: Aufwickeln und Abwickeln

Animation 1: Pythagoras-Lakritze

Wozu passt die Abwicklung?

Die Abbildung 1a zeigt eine Würfelabwicklung.

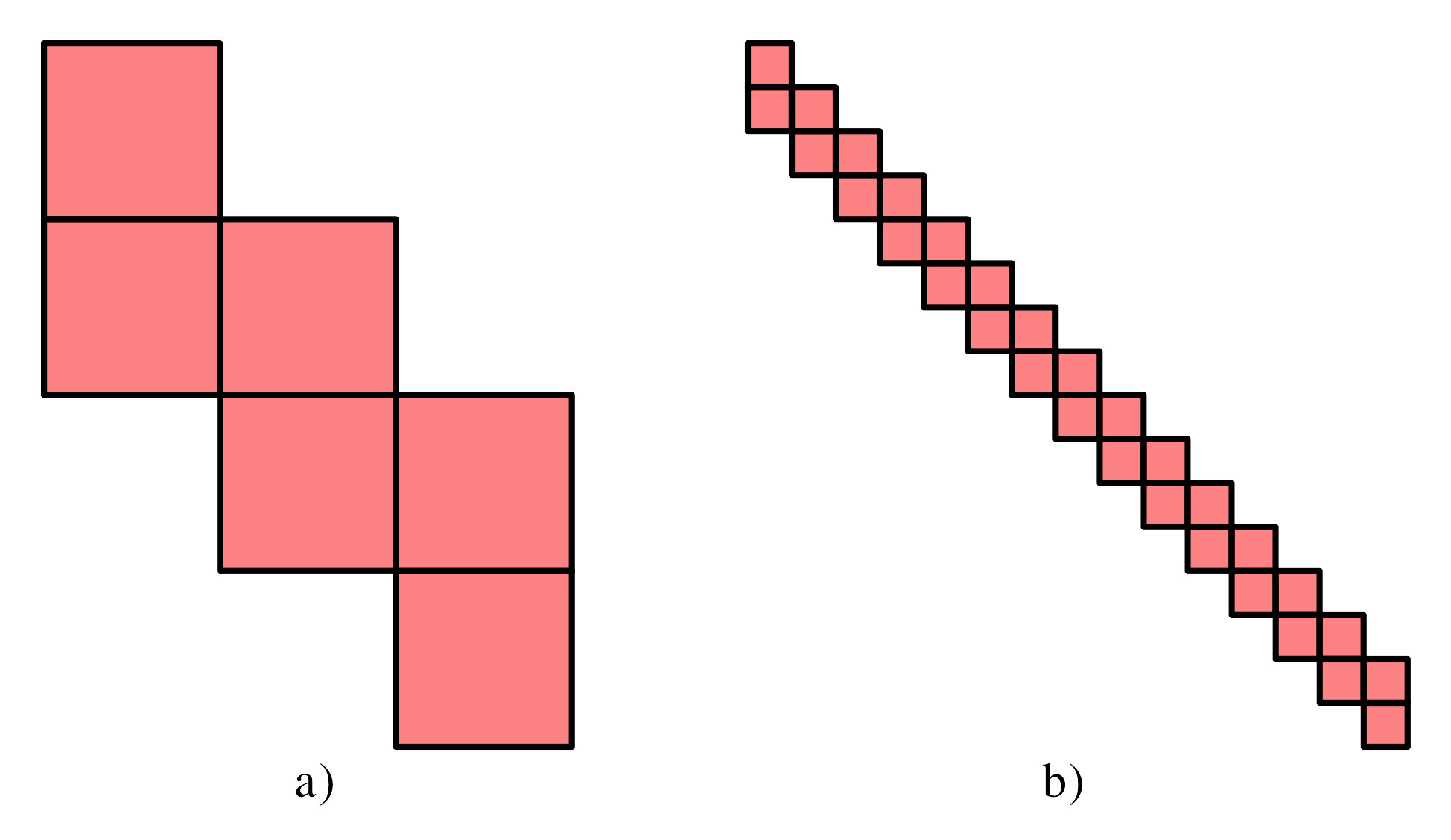
Abb. 1: Abwicklungen

Die fünfmal so lange Abwicklung der Abbildung 1b könnte entsprechend fünffach um den Würfel gewickelt werden – was allerdings Probleme mit der Kartondicke gäbe. Gibt es einen Körper mit der einfachen Abwicklung der Abbildung 1b? (Lösung siehe Abb. 7).

Würfelabwicklungen

Mein Enkel hat mir kürzlich unter die Nase gerieben, er habe neun von den elf Würfelnetzen (Abb. 2) selber herausgefunden. Er sagte Würfelnetz, so stehe es im Schulbuch.

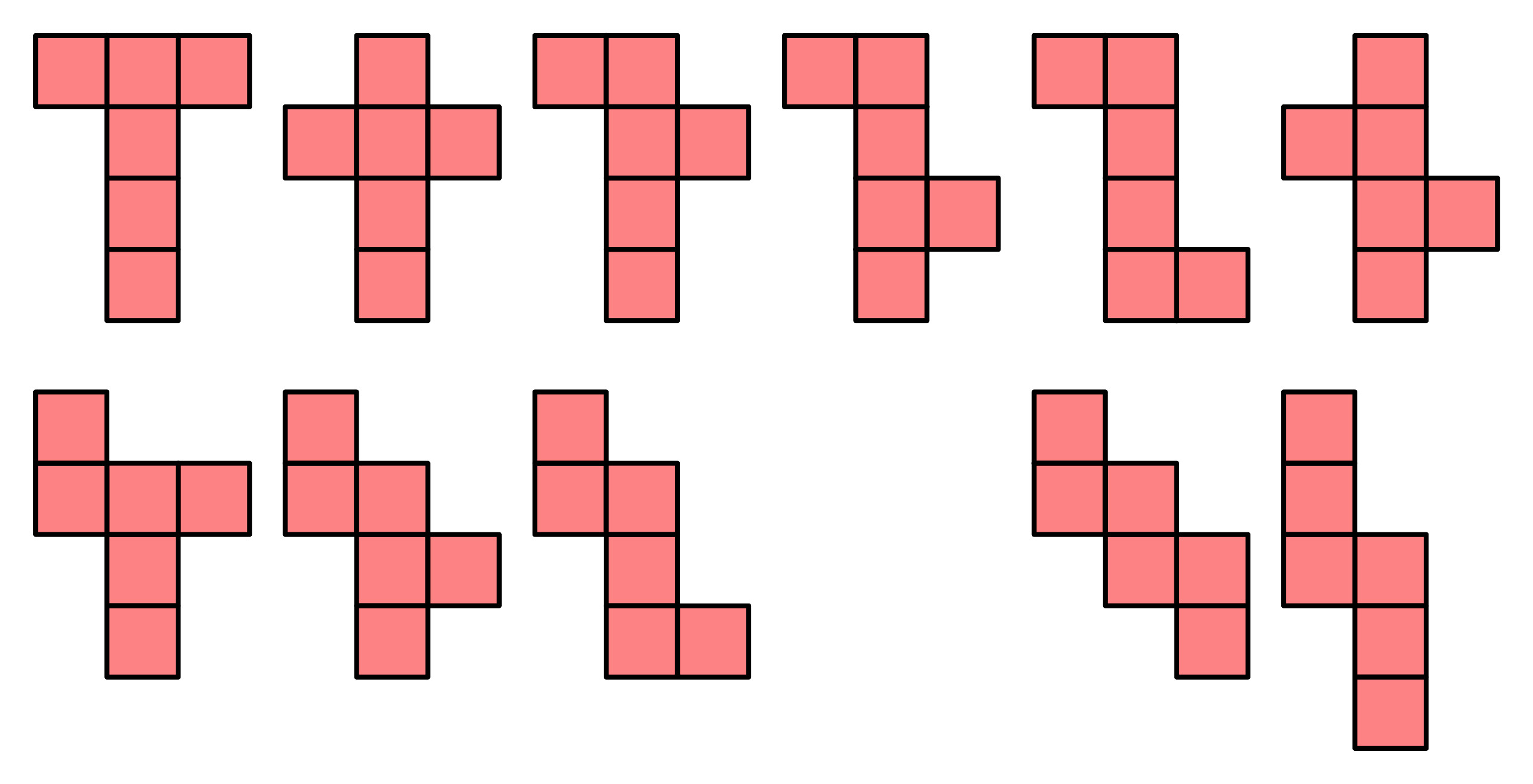
Abb. 2: Würfelabwicklungen

Die Bezeichnung „Netz“ für Polyederabwicklungen ist zwar in Schulbüchern geläufig, ist aber ein semantischer Ausreißer. Im Bedeutungsumfeld „Netz“ geht es immer um Knoten und deren Verbindungen. In den Abwicklungen der Abbildung 2 gibt es aber oft zwei oder gar drei Knoten, welche zur selben Würfelecke gehören. (Warum gibt es kein Beispiel, wo sogar vier Knoten zur selben Würfelecke gehören?) – Das widerspricht der Vorstellung eines Netzes. Man stelle sich einen Verkehrsnetzplan vor, in welchem der Hauptbahnhof zweimal vorkommt.

Die Abbildung 3 zeigt „echte“ Beispiele von Würfelnetzen.

Abb. 3: Würfelnetze

Klebelaschen

Für die Anordnung der Klebelaschen einer Polyederabwicklung gibt es eine einfache Regel. Bei jeder zweiten Kante auf dem Rand muss eine Klebelasche angebracht werden. Damit erhalten wir eine Vollverklebung.

Die Frage nach der Minimalverklebung ist spannender. Mit wie wenigen Klebelaschen hält das Polyeder gerade noch?

Bei den Würfelabwicklungen genügen in der Regel zwei Klebelaschen (exemplarisch in Abb. 4). Gleichfarbig markierte Kanten müssen mit einer Klebelasche verbunden werden. Bei zweien der elf Abwicklungen (rechts unten) genügt sogar eine Klebelasche.

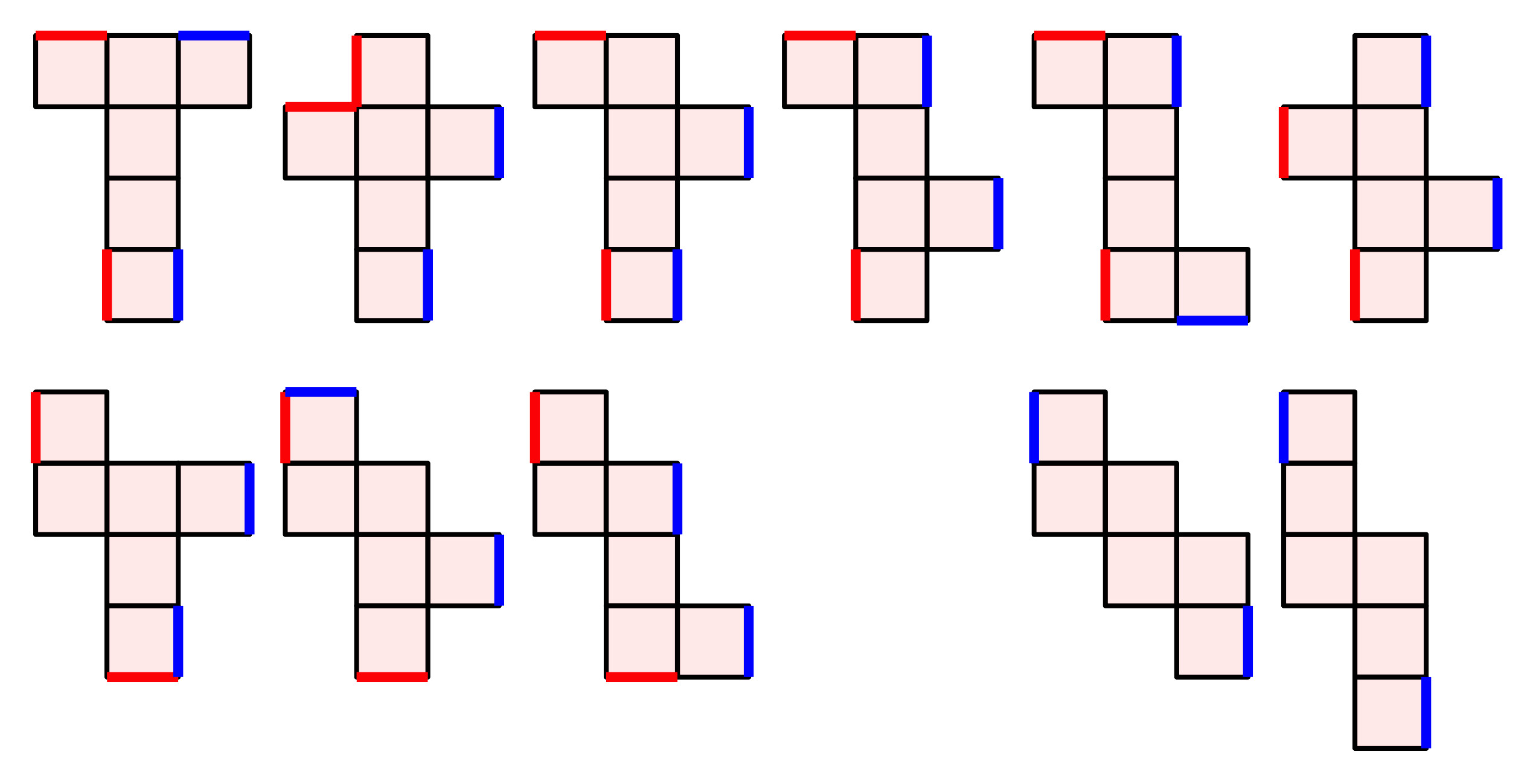
Abb. 4: Minimale Klebelaschen

Die Abbildung 5 zeigt ein Beispiel-Modell mit nur einer Klebelasche.

Abb. 5: Fahnenwürfel

Transmissionskette

Die Abwicklung der Abbildung 1b besteht aus fünf Abwicklungen der Abbildung 1a, welche an der einzigen nötigen Klebelasche zusammengeklebt sind. Solche verlängerte Abwicklungen können als Transmissionsketten verwendet werden (Abb. 6b). Die Zahnräder sind Würfel, welche auf einer Körperdiagonalen als Achse drehen (Abb. 6a).

Mein Enkel ist der Meinung, auf diese Weise könne man keine Übersetzungen bauen. Hat er recht?

Abb. 6: Transmission

Dreidimensionales Kreuz

Die Abwicklung der Abbildung 1b passt auf ein aus sieben Würfeln zusammengesetztes dreidimensionales Kreuz (Abb. 7). Ausprobieren!

Abb. 7: Dreidimensionales Kreuz

Aufwickeln auf einen Kreis

Wird ein gespannter Faden auf eine Spule aufgewickelt, beschreibt das Fadenende eine Evolvente (Abb. 8).

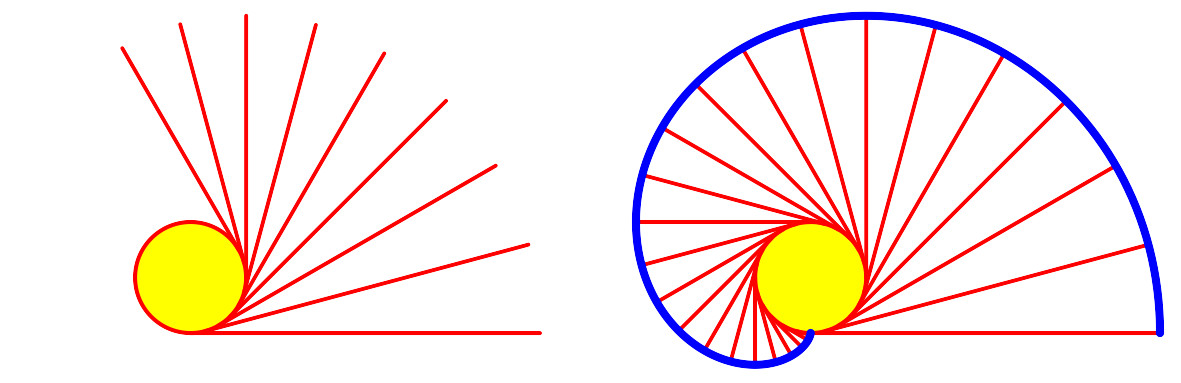
Abb. 8: Aufwickeln auf einen Kreis. Evolvente

Animation 2: Straffes Aufwickeln zum Kreis

Wir können aber auch so verfahren, dass der Faden gleichmäßig gekrümmt wird (Abb. 9).

Abb. 9: Gleichmäßig gekrümmt

Animation 3: Gleichmäßig gekrümmt

Das Fadenende beschreibt eine Kurve mit der Polargleichung:

(0)

Die Kurve kann zu einer Herzkurve ergänzt werden (Abb. 10a). Diese ist etwas größer als die klassische Kardioide (Abb. 10b).

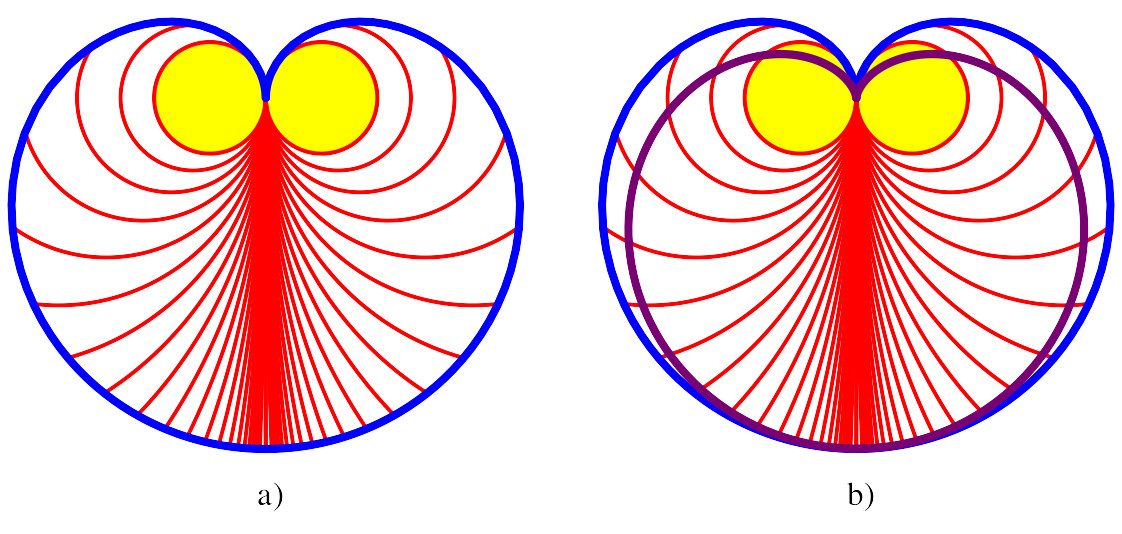
Abb. 10: Herzkurve. Vergleich mit Kardioide

Aufwickeln auf ein Dreieck

Beim Aufwickeln mit gespanntem Faden auf ein Dreieck läuft das Fadenende auf einer Folge von Kreisbögen mit schrittweise abnehmendem Radius (Abb. 11).

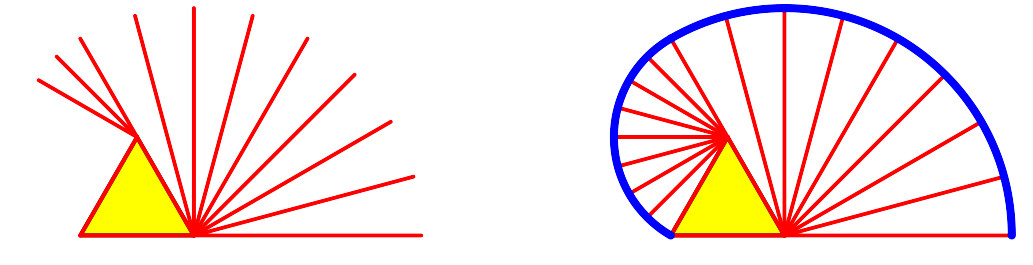
Abb. 11: Folge von Kreisbögen

Animation 4: Straffes Aufwickeln zum Dreieck

Nun wickeln wir so auf, dass wir den Faden gleichmäßig knicken (Abb. 12). An den Knickstellen sollen die Außenwinkel gleichmäßig zunehmen.

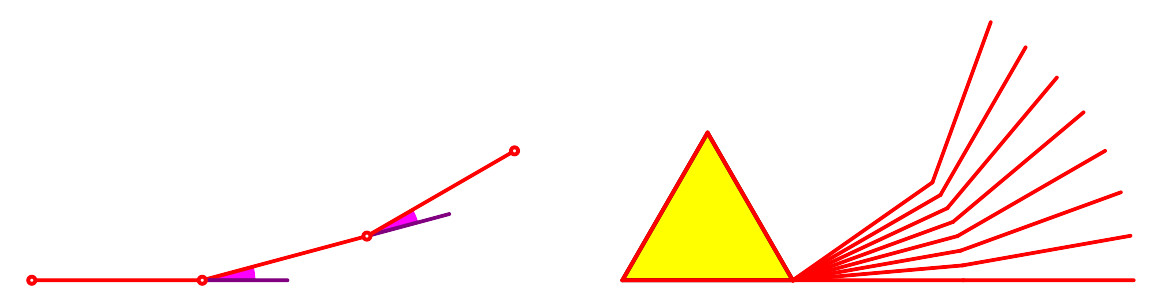
Abb. 12: Gleichmäßig geknickt

Animation 5: Gleichmäßig geknickt

Wir können das sehen wie das Schließen einer flachen Hand zur Faust. Bei der Hand haben wir allerdings – vom Handrücken aus gezählt – vier Teile, und diese sind nicht von gleicher Länge.

Animation 6: Bahnkurven

Animation 7: Durchgedreht

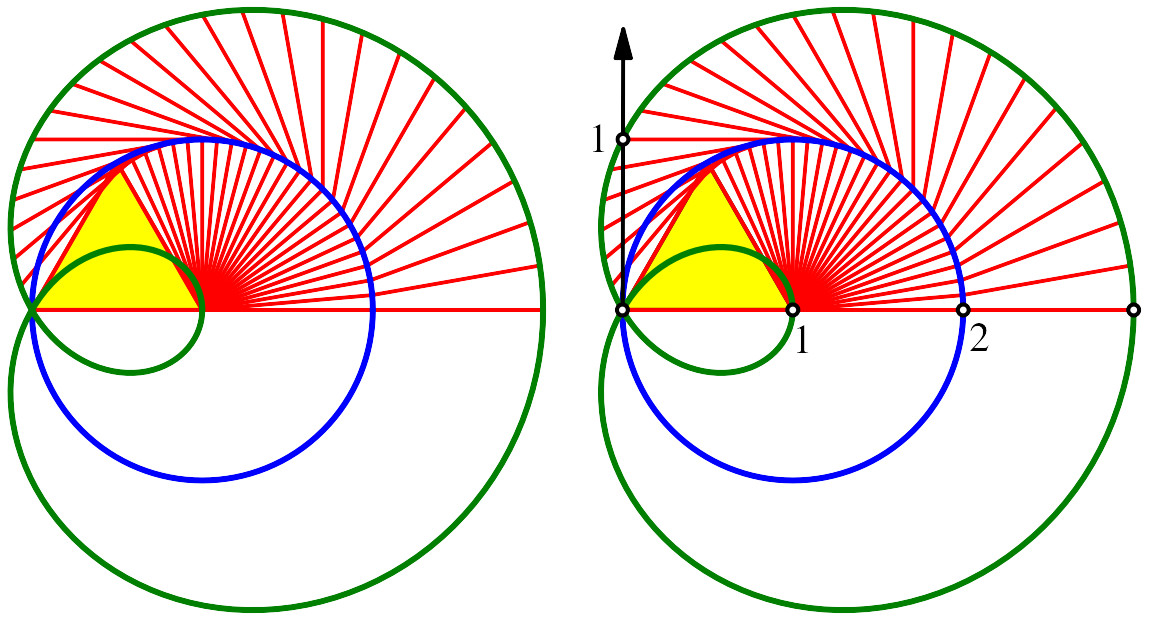
Abb. 13: Kreisüberlagerung

Die erste Knickstelle ist ortsfest. Die zweite Knickstelle läuft auf einem Kreis. Der Endpunkt des äußersten Schenkels läuft auf einer Kurve, welche eine Kreisüberlagerung darstellt. Auf dem ersten Kreis läuft der Mittelpunkt des zweiten Kreises, der mit doppelter Geschwindigkeit dreht.

Im eingezeichneten Koordinatensystem kann die entstehende Kurve parametrisiert werden wie folgt 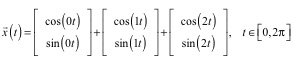(1).

(1)

Wir sehen eine Fourier-Folge, die nach zwei Schritten abbricht.

Die Abbildung 14 zeigt ein mechanisches Modell mit Zahnrädern.

Das ganz große Zahnrad sitzt im Leerlauf auf einer gerätefesten Achse und wird von unten (kleines Zahnrad) angetrieben. Es dient dem Anheben des ersten bewegten Schenkels. Auf derselben Achse sitzt vorne ein ortsfestes Zahnrad. Dieses dreht sich also gegenüber dem Gerät nicht. Durch das Anheben des beweglichen Schenkels wird aber über zwei kleine Zwischenzahnräder das äußerste Zahnrad angetrieben. Dieses dreht doppelt so rasch wie der bewegliche Schenkel (Übergang von t zu 2t in der Parameterdarstellung). Dieses äußerste Zahnrad bewegt den äußeren Schenkel des Gerätes. Die Bewegung des äußersten Punktes dieses Schenkels entspricht der Kreisüberlagerung der Abbildung 13.

Die beiden kleinen Zwischenzahnräder dienen nur zur Verlängerung des ersten beweglichen Schenkels. Für die Kinematik sind sie unerheblich und könnten weggelassen werden.

Abb. 14: Mechanisches Modell

Hundekurve

Die Kurve der Abbildung 13 ist eine „Hundekurve“. Wir legen die Wurst in den Doppelpunkt. Wenn nun die Madame mit dem Fiffi an der roten Einheitsleine auf dem blauen Kreis spazieren geht, bewegt sich der Fiffi auf der inneren Schleife der grünen Kurve (Abb. 15). Der zweite Hund der Madame, der Veggi, bewegt sich auf der äußeren Schleife.

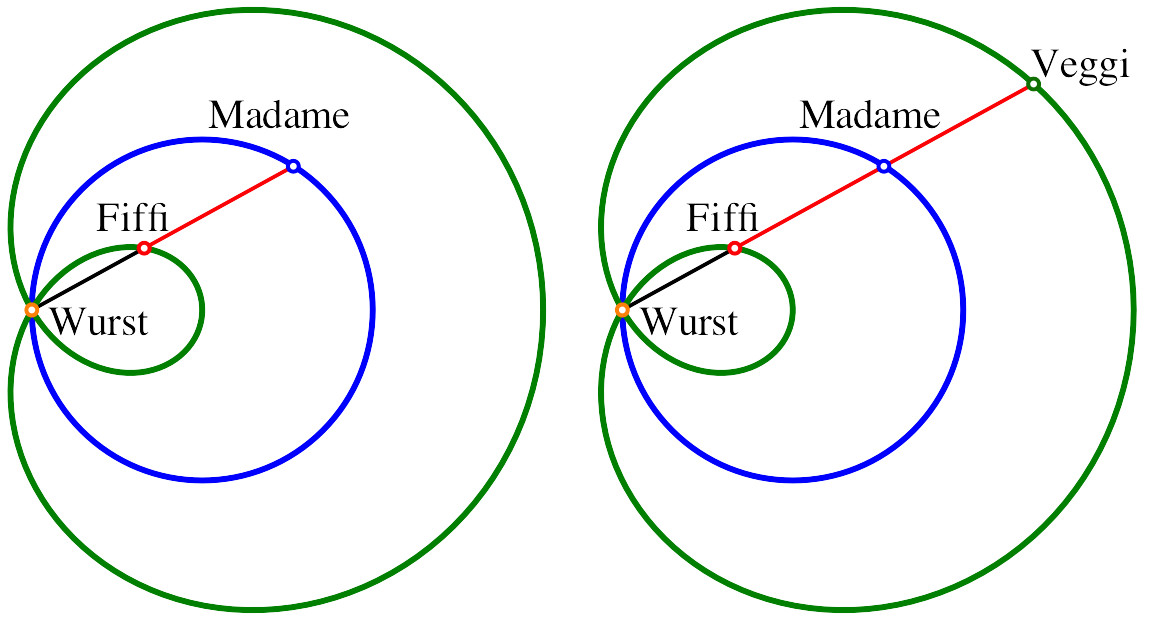
Abb. 15: Fiffi und Veggi

Animation 8: Wurst, Fiffi, Madame und Veggi

Bevor wir das beweisen, zwei mechanische Modelle. In beiden Modellen stellt die blaue Kreisscheibe die Madame dar, die rote Kreisscheibe den Fiffi, die grüne Kreisscheibe den Veggi und die orange Kreisscheibe die Wurst.

Im Modell der Abbildung 16 ist eine Führungsstange sichtbar, welche den Fiffi zur Wurst leitet. Allerdings haben wir dort einen Anschlag, und es geht nicht mehr weiter.

Abb. 16: Führungsstange mit Anschlag

Im Modell der Abbildung 17 sind Führungsstange und Wurst eine Ebene nach vorne verlegt. Daher kann, wenn der Fiffi die Wurst erreicht hat, weitergedreht werden. Der Fiffi entfernt sich dann auf der äußeren Schleife von der Wurst. Als nächstes erreicht die Madame die Wurst. Das ist der „tote Punkt“ des Modells. Die beiden Hunde könnten in dieser Situation vertauscht werden. Das Weiterdrehen funktioniert aber über diesen toten Punkt hinweg. Nun nähert sich der Veggi der Wurst und erreicht sie. Anschließend bewegt er sich auf der inneren Schleife, bis er wieder die Wurst erreicht. Durch Weiterdrehen erhalten wir schließlich die Ausgangsposition mit dem Fiffi auf der inneren und dem Veggi auf der äußeren Schleife.

Abb. 17: Führungsstange nach vorn verlegt

Beweis

Wir haben zu zeigen, dass die Kurve der Abbildung 13 mit der Parametrisierung (1) tatsächlich eine Hundekurve ist.

Wir bezeichnen wie schon früher mit t den Parameter des blauen Kreises, also für die Bewegung der Madame. Im gelb eingezeichneten gleichschenkligen Dreieck ist dies der Außenwinkel des Spitzenwinkels. Die beiden Basiswinkel sind je halb so groß.

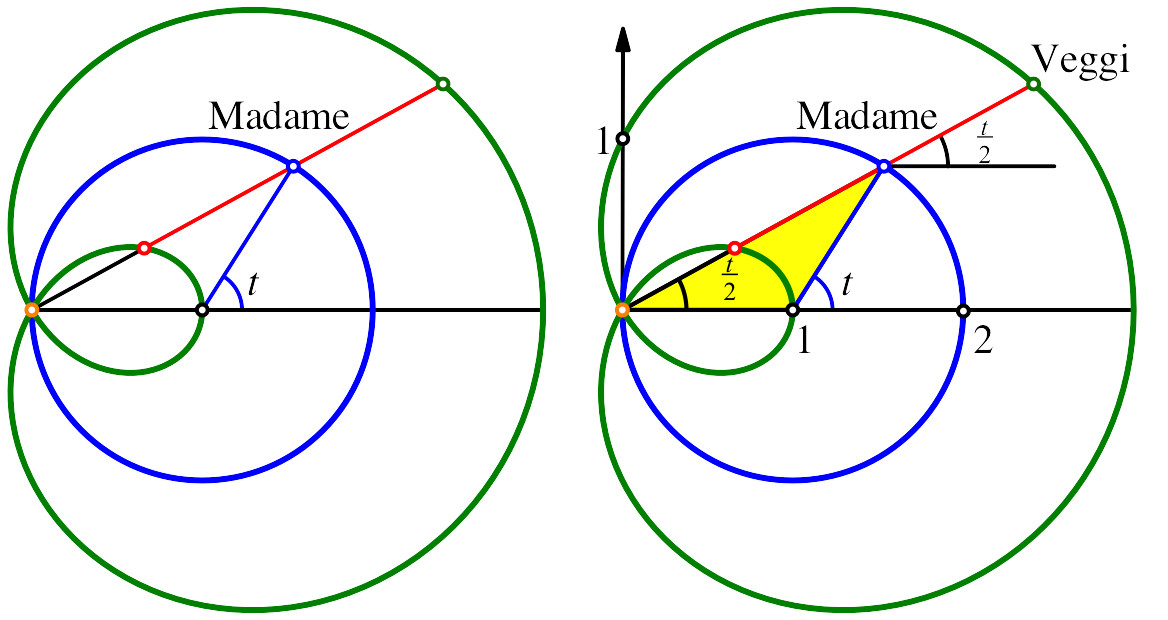
Abb. 18: Parametrisierung der Hundekurve

Mit Hilfe des parallel verschobenen Basiswinkels kann nun die Bewegung des Veggi parametrisiert werden. Es ist:

(2)

Der Vergleich der Parametrisierungen (1) und (2) ist zunächst irritierend. Die ersten beiden Summanden sind (scheinbar) identisch, im letzten Summanden haben wir einmal das Doppelte und einmal die Hälfte des Parameters.

Das Problem löst sich mit einer Parametertransformation. Wenn wir in (1) den Parameter durch einen doppelt so großen substituieren und den zweiten und dritten Summanden vertauschen, ergibt sich (2). Auch die Parameterbereiche stimmen dann wieder überein. Damit ist der Beweis erbracht.

Der Autor gesteht, dass nicht nur seine Studierenden, sondern auch er selber Probleme mit solchen Parametertransformationen hat. Man muss mit einer Hilfsvariablen arbeiten, die man am Schluss dann umbenennt.

Ein Diskussionspunkt ist die Frage, ob zwei durch verschiedene Parametrisierungen beschriebene, aber identische Punktmengen als dieselbe Kurve bezeichnet werden können. Fundamentalisten verneinen dies. Für eine Kurve ist die Parametrisierung essentiell, so wie der Definitionsbereich zum Funktionsbegriff gehört. Geometer und Kartografen haben da weniger Skrupel. Wien bleibt Wien, egal ob auf der Plattkarte oder der Mercator-Karte.

Die Parametrisierung (2) gibt Anlass zu einem weiteren mechanischen Modell für die Kurve (Abb. 19).

Abb. 19: Ein weiteres Modell für die Hundekurve

Die Wurst ist hier mechanisch völlig isoliert. Das Modell funktioniert mit einem Kettengetriebe. Das äußere Kettenrad ist doppelt so groß wie das innere. Es dreht daher halb so schnell. Dies liefert den halben Parameter im letzten Summanden von (2). Das Rädchen mit dem schwarzen Gummireifen ist nur ein Kettenspanner. Er ist erforderlich, damit das Modell präzis genug arbeitet. Über Hundekurven und verwandte Kurven siehe Haftendorn (2017), S. 38-78.

Winkeldrittelung

Die Parametrisierungen (1) und (2) ergeben global dieselben Punkte, aber nicht punktweise. Für einen bestimmten Parameterwert ergeben sich zwei verschiedene Punkte, die aber beide auf der Kurve liegen (Abb. 20).

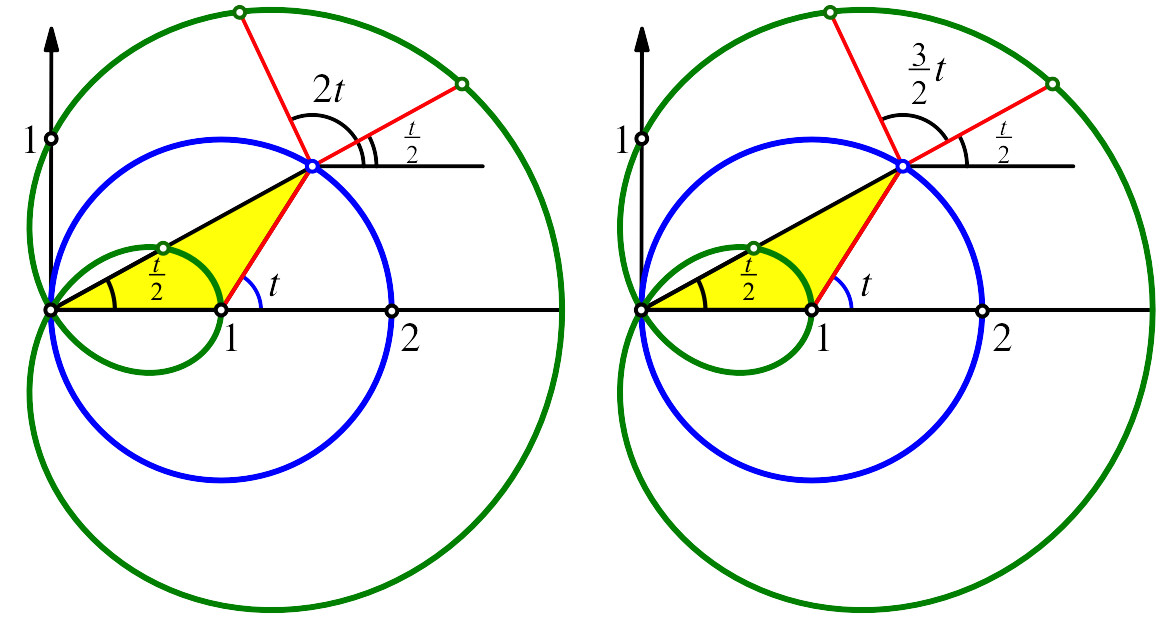
Abb. 20: Verschiedene Punkte

Bis zum Punkt auf dem blauen Kreis unterscheiden sich die beiden Parameterdarstellungen nicht. Mit der Parametrisierung (1) erhalten wir dann aber gegenüber der Horizontalen einen Winkel von 2t und für denselben Parameterwert mit der Parametrisierung (2) einen Winkel von . Die Differenz ist , also das Dreifache des kleinen Winkels . Damit ergibt sich eine Möglichkeit zur Winkeldrittelung.

Sie geht so: Wir zeichnen gemäß Abbildung 21 ein gleichschenkliges Dreieck mit dem zu drittelnden Winkel als Spitzenwinkel. Dieses Dreieck passen wir dann so ein, dass auch die zweite Basisecke auf der Kurve liegt. Der Winkel zur Horizontalen durch die Dreiecksspitze ist dann ein Drittel des Ausgangswinkels.

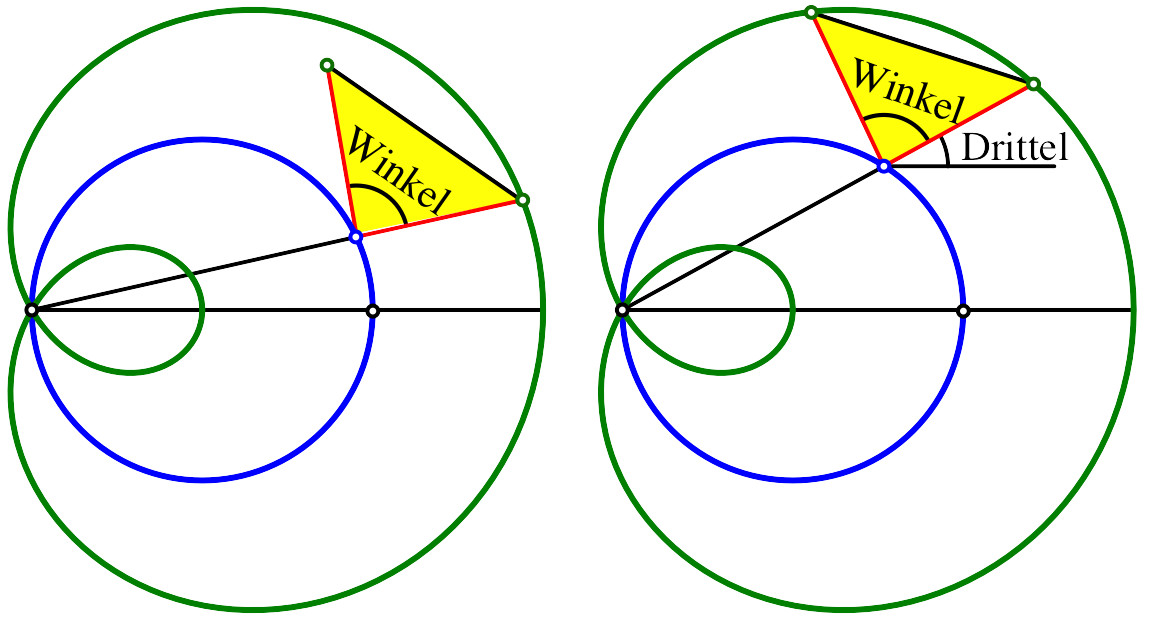
Abb. 21: Winkeldrittelung

Berührung der Dreiecksspitze

In der Abbildung 13 sehen wir, dass der äußere Schenkel die Dreiecksspitze zunächst berührt und dann überschneidet. Bei welchem Parameterwert t findet die Berührung (Abb. 22) statt?

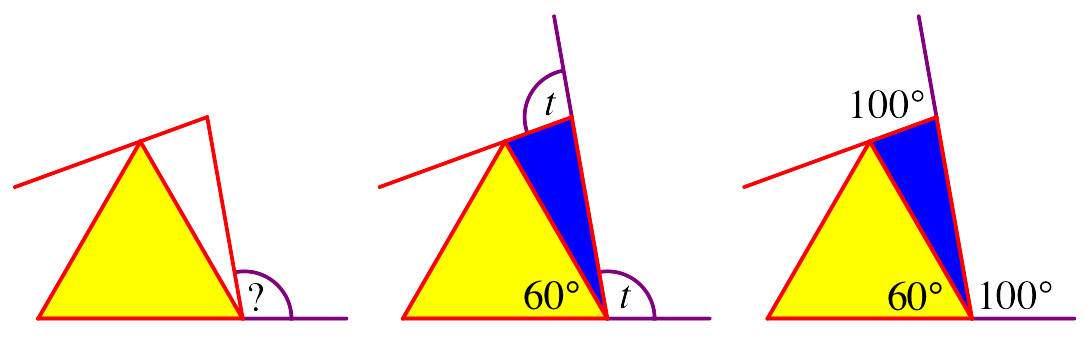
Abb. 22: Berührung

Wir machen eine Außenwinkelüberlegung im blau eingezeichneten gleichschenkligen Dreieck. Der gesuchte Parameterwert t ist der Außenwinkel der Basiswinkel. Der Spitzenwinkel hat den Außenwinkel t + 60°. Die Summe der drei Außenwinkel ist also 3t + 60°. Da umgekehrt in jedem Vieleck die Summe der Außenwinkel 360° beträgt, ergibt sich t = 100°.

Ich habe in meinem bisherigen Leben noch nie einen Winkel von 100° angetroffen. Dies liegt wohl daran, dass ein solcher Winkel nicht mit Zirkel und Lineal konstruierbar ist. Der Beweis dazu verläuft indirekt. Angenommen, ein Winkel von 100° sei mit Zirkel und Lineal konstruierbar. Dann ließe sich ein Winkel von 60° subtrahieren und wir erhielten einen Winkel von 40°, alles mit Zirkel und Lineal. Dies ist der Zentriwinkel eines regelmäßigen Neunecks, welches damit ebenfalls mit Zirkel und Lineal konstruierbar wäre. Das widerspricht aber einem Satz von Gauß über die Konstruierbarkeit regelmäßiger Vielecke.

Das rechnerische Vorgehen führt auf kubische Gleichungen.

Das analoge Problem beim Aufwickeln auf ein Quadrat (Abb. 23) führt nicht auf einen „schönen“ Winkel. Die zugehörigen Gleichungen sind vom Grad 12.

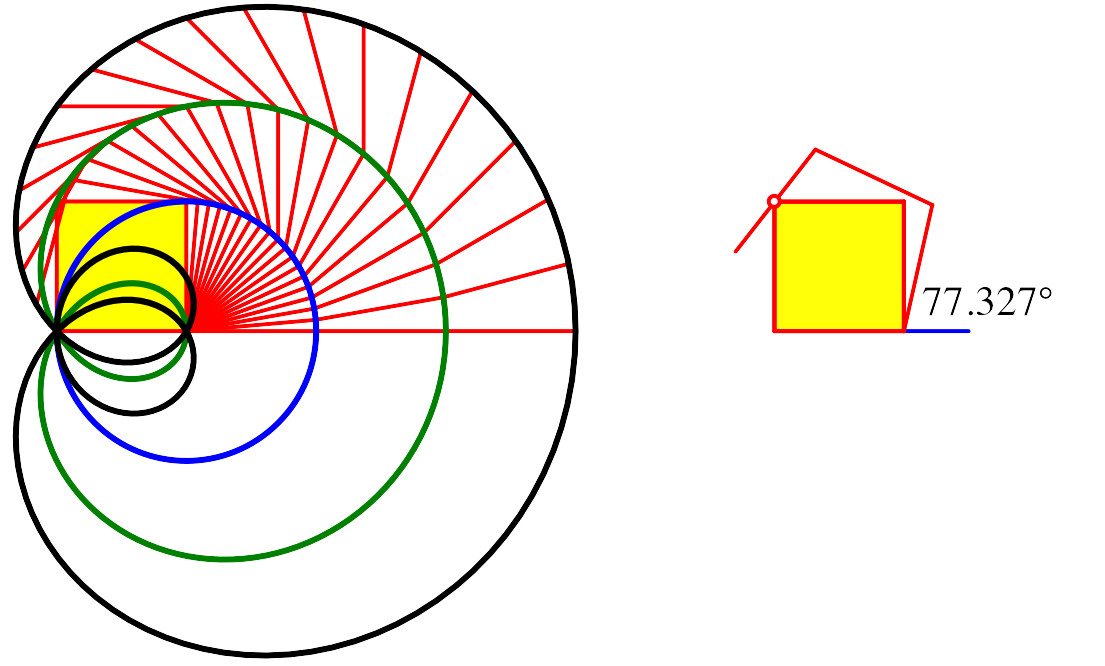
Abb. 23: Auf ein Quadrat aufwickeln.

Aufwickeln auf einen Würfel

Wir wickeln nun die Abwicklung der Abbildung 1a gleichmäßig geknickt auf den Würfel. Die Abbildung 24 zeigt die Startlage und den ersten Schritt mit einer Drehung um 5°. Das vorderste Quadrat bleibt ortsfest. Dann wird um jede Kante, welche zwei Quadrate verbindet, je um 5° gedreht. Das heißt, dass zwar die erste Drehachse auch ortsfest bleibt, aber schon die zweite Drehachse und mit ihr alle folgenden Drehachsen verdreht werden. Wir haben dieselbe Situation wie bei einem Roboter, der mehrere Drehachsen hat, welche sukzessive verdreht werden.

Abb. 24: Start und Drehung um 5°

Die Abbildung 25 zeigt die Situation nach Drehungen um 40° und um 45°.

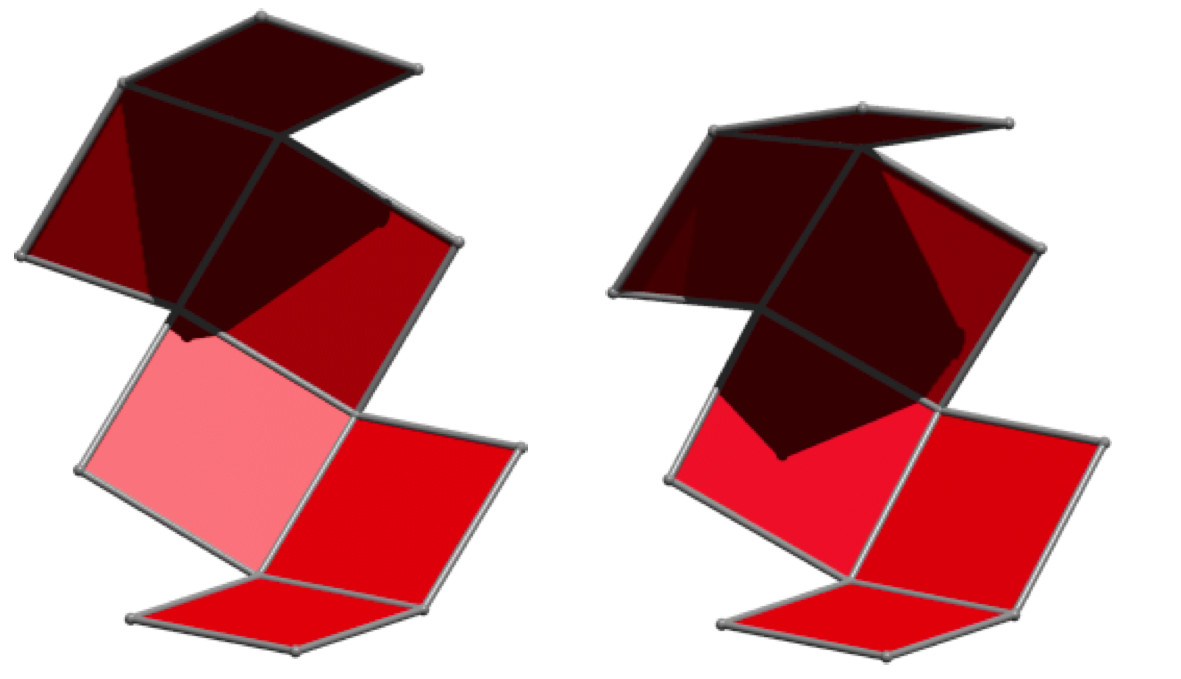
Abb. 25: Drehungen um 40° beziehungsweise 45°

In der Abbildung 26 haben wir die Situation nach der Drehung um 85° und schließlich die Endlage des Würfels.

Abb. 26: Drehung um 85° und geschlossener Würfel

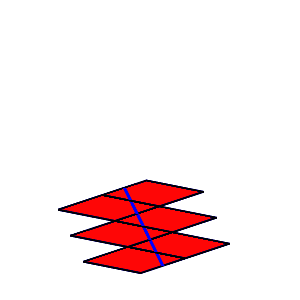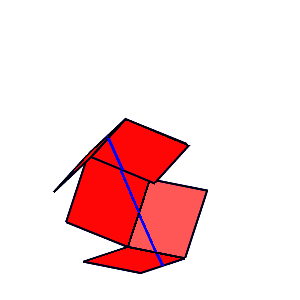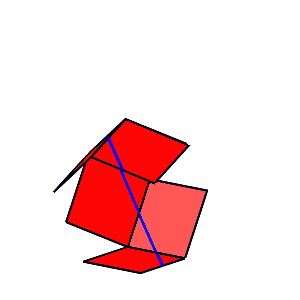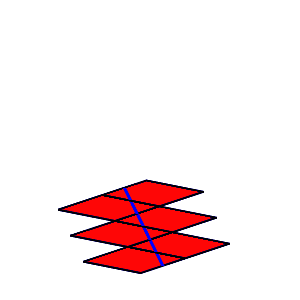
Animation 9: Aufwickeln zum Würfel

Berührung einer Würfelecke

Analog zu den Abbildungen 22 und 23 interessiert die Frage, ob und wo der einzupackende Würfel berührt wird. Ich bin diese Frage nur experimentell angegangen. Die Abbildung 27 zeigt die Startposition mit dem Würfel und die erste feststellbare Durchschneidung bei einer Drehung von etwa 70°.

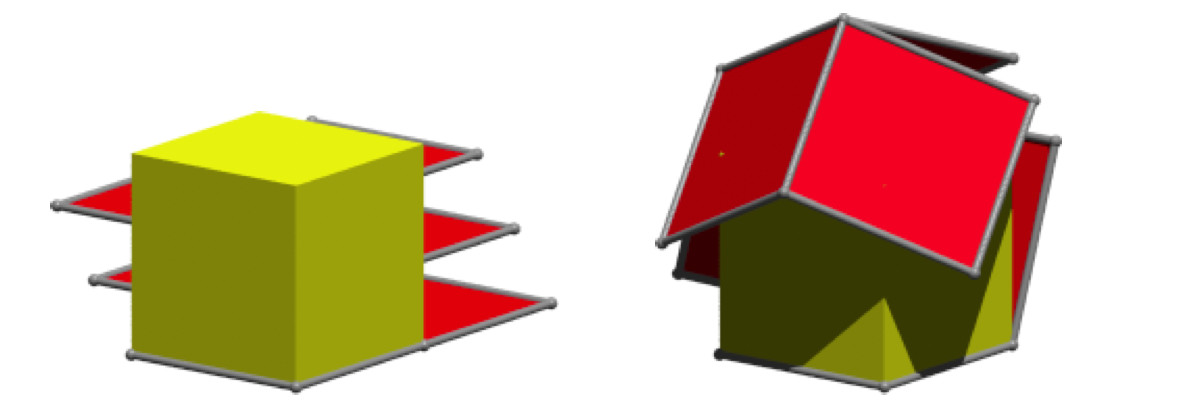
Abb. 27: Start und Beginn der Würfeldurchdringung bei etwa 70°

In der Abbildung 28 sehen wir die beiden Folgeschritte.

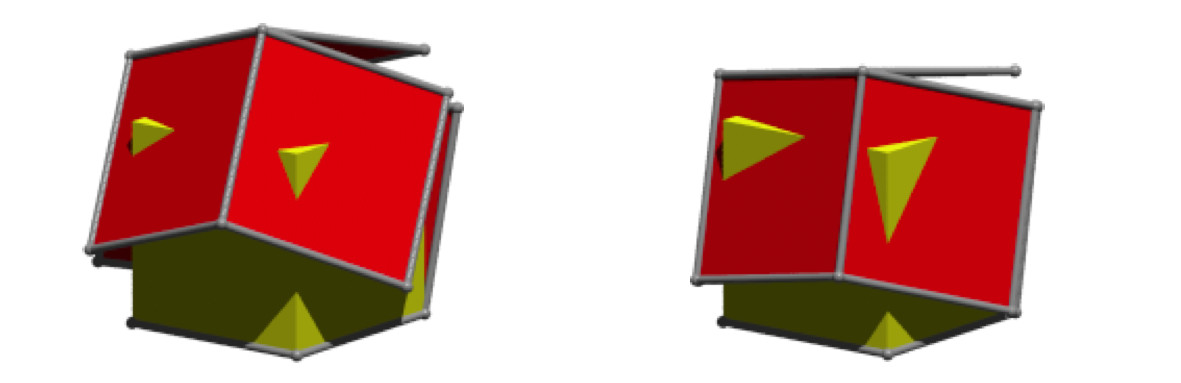
Abb. 28: Drehungen um 75° respektive 80°

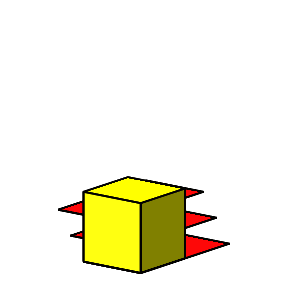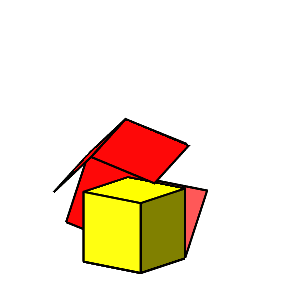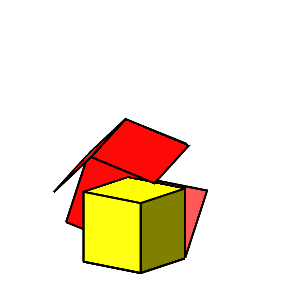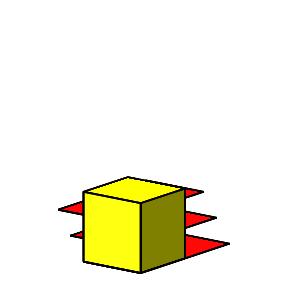
Animation 10: Würfeldurchdringung

Literatur

Haftendorn, Dörte (2017): Kurven erkunden und verstehen. Mit GeoGebra und anderen Werkzeugen. Wiesbaden: Springer Spektrum. ISBN 978-3-658-14748-8.

Websites

Hans Walser: Fahnenwürfel

www.walser-h-m.ch/hans/Miniaturen/F/Fahnenwuerfel/Fahnenwuerfel.htm

Hans Walser: Aufwickel-Pythagoras

www.walser-h-m.ch/hans/Miniaturen/A/Aufwickel-Pythagoras2/Aufwickel-Pythagoras2.htm

Hans Walser: Aufwickel-Pythagoras

www.walser-h-m.ch/hans/Miniaturen/A/Aufwickel-Pythagoras/Aufwickel-Pythagoras.htm