Hans Walser

Bewegte Figuren

Tag der Geometrie

Do, 13. April 2023, Graz

Abstract

Im Sinne einer kinematischen Geometrie werden Bahnkurven von Schnittpunkten bewegter Geraden analysiert. Dabei treffen wir auf Kreise und weitere Kegelschnitte, aber auch auf weniger bekannte Kurven.

Viele Beispiele können mit dynamischer Geometrie Software einfach dargestellt werden.

Keywords: Thaleskreis, Ortsbogen, Strophoide, Kiepert-Punkte, Kiepert-Hyperbel, Euler-Gerade, Kreisumfang, Zykloide, bewegte Kamera, Rosetten

1 Was war zuerst?

Was war zuerst: der Thaleskreis oder der rechte Winkel?

Rechter Winkel und Thaleskreis

2 Gleiche Frequenzen

Wir drehen zwei Geraden um die Drehzentren A₁(1,0) und A₂(–1,0) mit den Drehwinkeln w₁t + p₁ beziehungsweise w₂t + p₂. Dabei sind w₁ und w₂ die Drehfrequenzen, p₁ beziehungsweise p₂ allfällige Phasenverschiebungen und t der Drehparameter.

Wir untersuchen die Bahnkurven des Schnittpunktes der beiden gedrehten Geraden.

Bei gleichen Frequenzen und einer Phasendifferenz von 90° ergibt sich der Thaleskreis. Bei einer Phasendifferenz von 120° ergibt sich der Ortsbogen für 120° über der Strecke A₁A₂. Der Winkel 120° ist gegebenenfalls als Außenwinkel zu sehen.

Phasendifferenz 120°: Ortsbogen

Eine Uraltaufgabe im Schulunterricht besteht ja darin, die beiden Punkte A₁ und A₂ als Leuchttürme zu sehen, deren Leuchten gleich schnell aber mit einer Phasendifferenz drehen. Der zugehörige Ortsbogen soll die Gefahrenzone abgrenzen. Je nachdem welche Leuchtturmsignatur von der Brücke aus zuerst gesehen wird, befindet sich das Schiff innerhalb oder außerhalb der Gefahrenzone. Den Ortsbogen selber sieht man nicht.

Lehrer sind wie Leuchttürme. Sie weisen den Weg, ohne selber hinzugehen.

3 Ungleiche Frequenzen

Ein Kreis kann auch mit einem Frequenzverhältnis 2:1 erreicht werden.

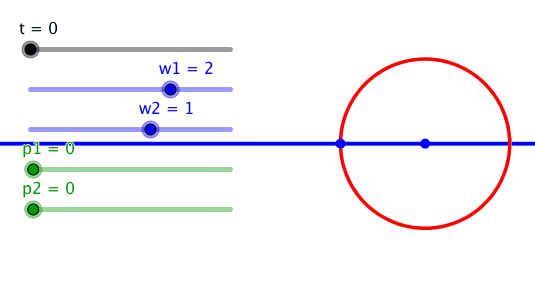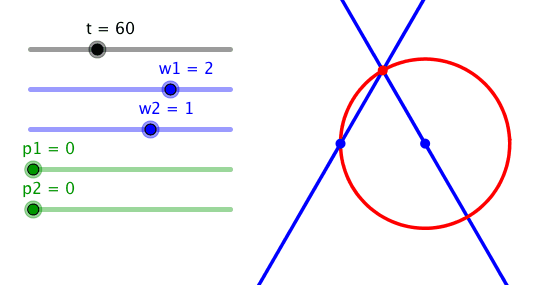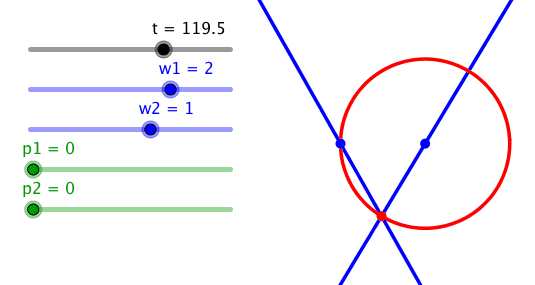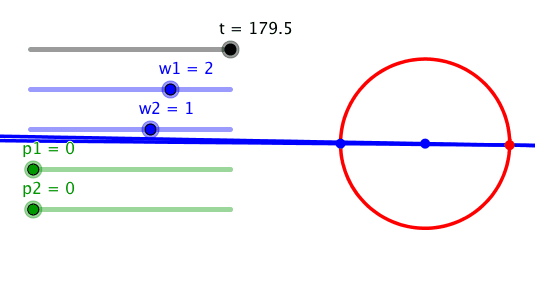
Frequenzverhältnis 2:1

Dies wird sofort einsichtig durch Einzeichnen eines gleichschenkligen Dreieckes. Der Außenwinkel 2t an der Spitze ist gleich der Summe der beiden innenliegenden Basiswinkel t.

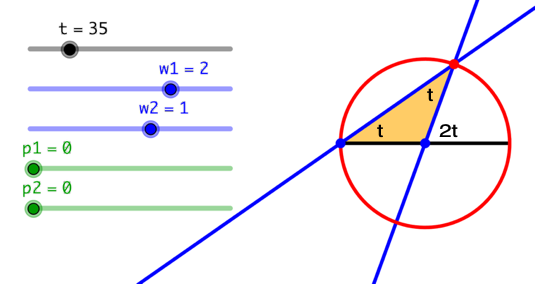
Gleichschenkliges Dreieck

Wird noch zusätzlich eine Phasendifferenz von 90° eingebaut, ergibt sich die sogenannte Strophoide.

Wenn die gedrehten Geraden momentweise parallel sind, ergibt sich ein unendliche ferner Schnittpunkt. Daher hat die Strophoide eine Asymptote (hellgrün).

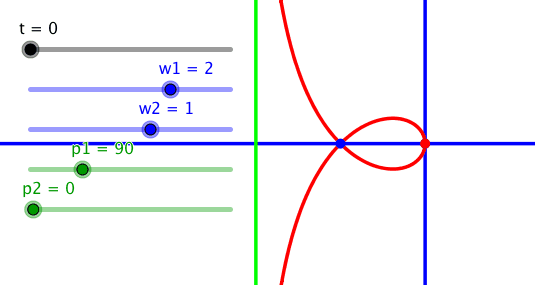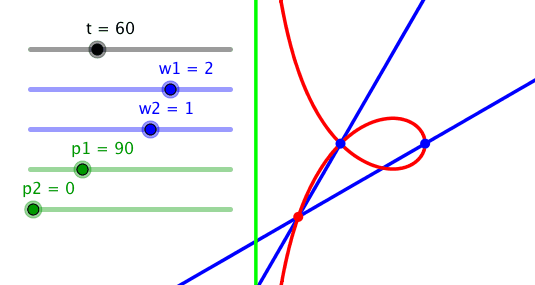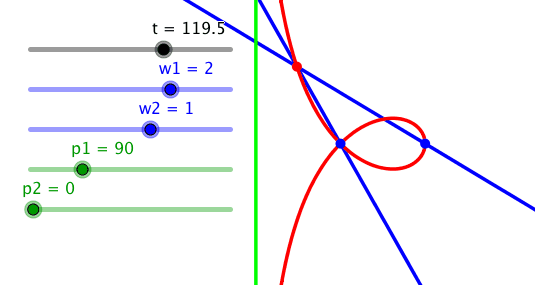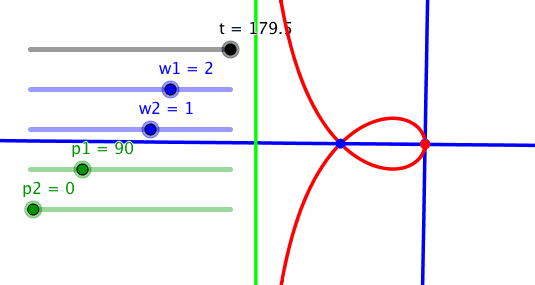
Strophoide

4 Verallgemeinerung

Bei einem Frequenzverhältnis 3:1 und einer Phasendifferenz 90° ergibt sich eine Kurve mit einem Tripelpunkt.

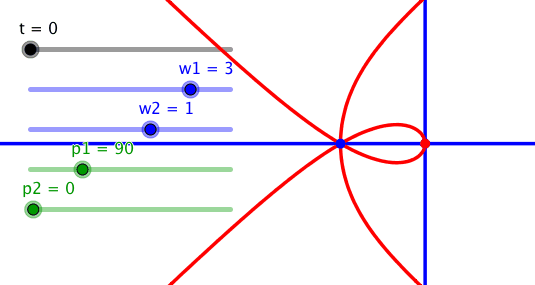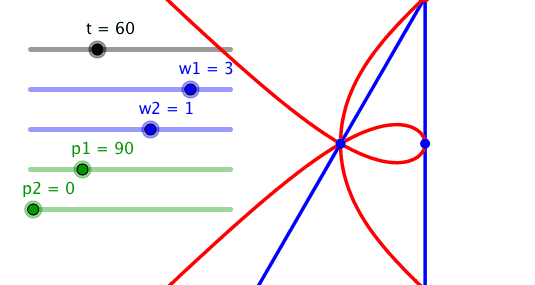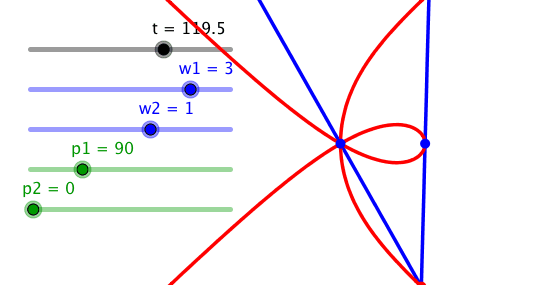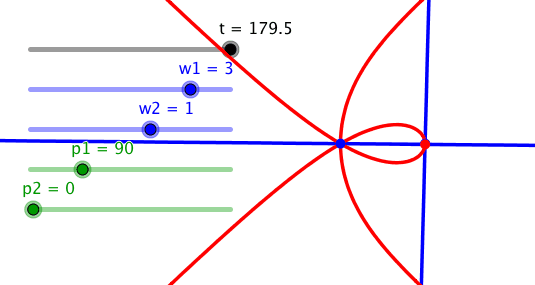
Tripelpunkt

Im Tripelpunkt entstehen Winkel von 60°.

5 Entgegengesetzter Drehsinn

Bei entgegengesetzt gleichen Frequenzen und der Phasendifferenz null ergibt sich als Bahnkurve des Schnittpunktes die Mittelsenkrechte der Strecke A₁A₂.

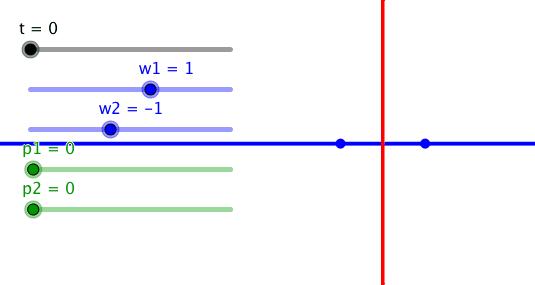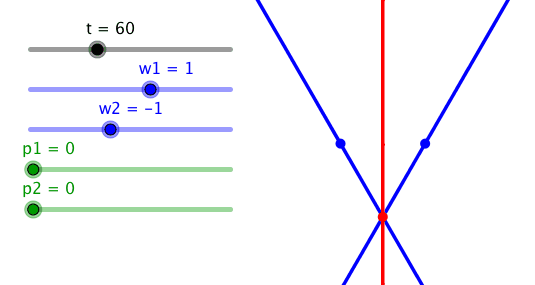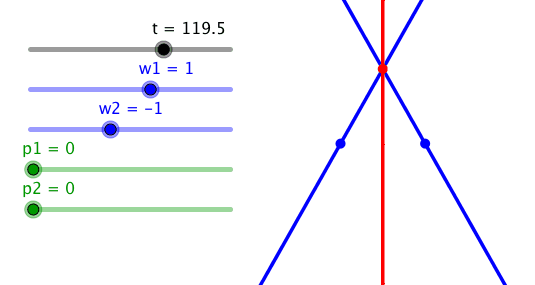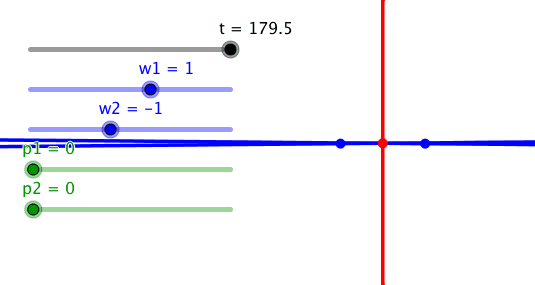
Entgegengesetzt gleiche Frequenzen: Mittelsenkrechte

Mit den Frequenzen 1 und –2 sowie der Phasendifferenz null ergibt sich eine Hyperbel. Die Asymptoten-Richtungen sind die Richtungen paralleler Drehgeraden. Die Figur ist das Pendant zum Kreis, der sich aus dem Frequenzverhältnis 2:1 ergibt.

Hyperbel

Bei entgegengesetzt gleichen Frequenzen und der Phasendifferenz 90° erhalten wir eine gleichseitige Hyperbel. Bei einer gleichseitigen Hyperbel schneiden einander die Asymptoten rechtwinklig. Die Figur ist das hyperbolische Pendant zum Thaleskreis.

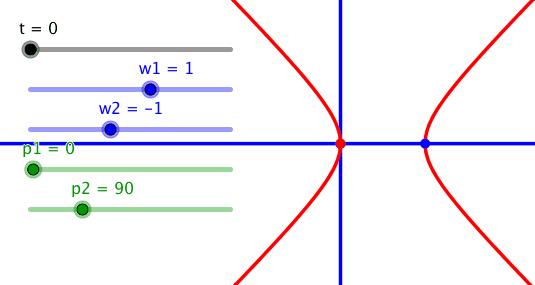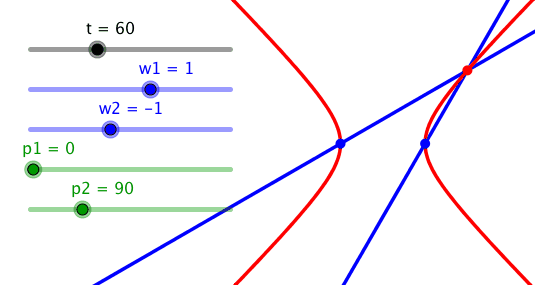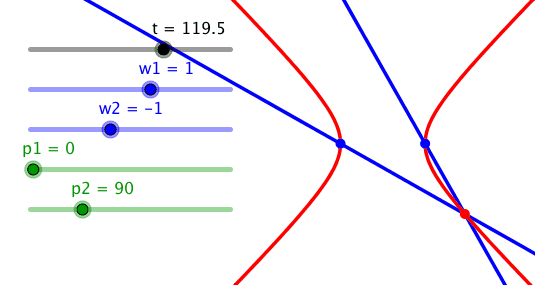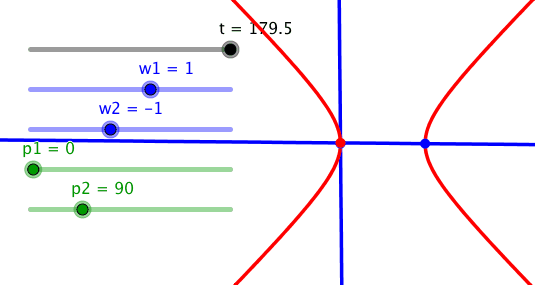
Gleichseitige Hyperbel

Bei der Phasendifferenz 120° hängt die gleichseitige Hyperbel schief im Koordinatensystem. Die Figur ist das hyperbolische Pendant zum Ortsbogen.

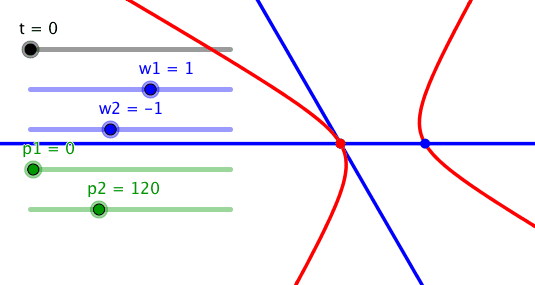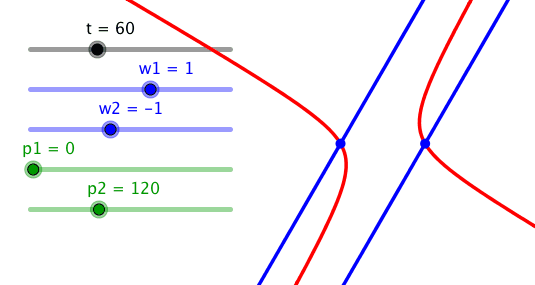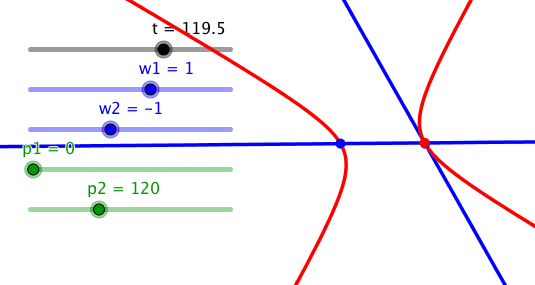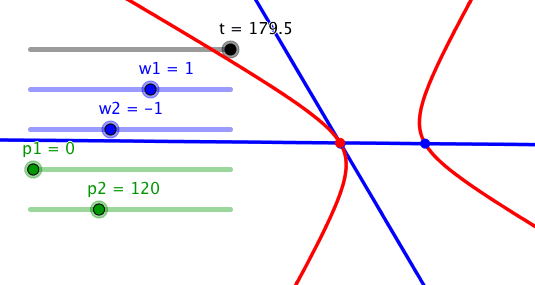
Schief gehängte gleichseitige Hyperbel

Bei Frequenzen 4 und –3 und der Phasendifferenz 60° ergibt sich eine Figur mit einem Quadrupelpunkt und einem Tripelpunkt.

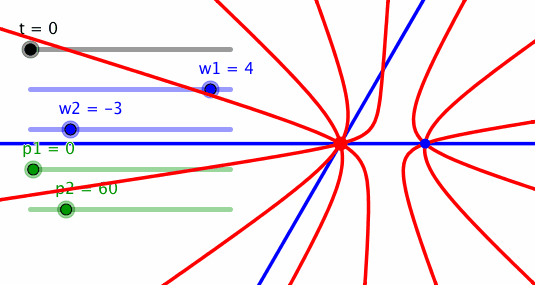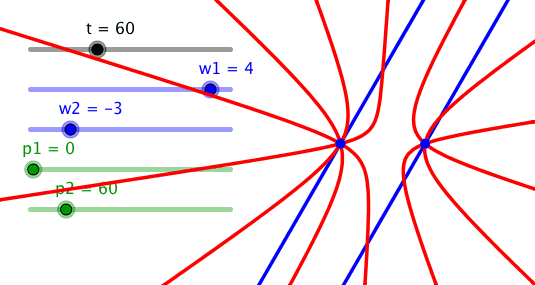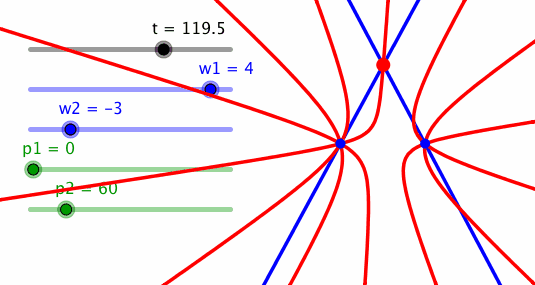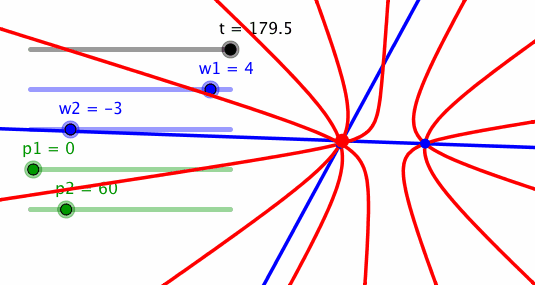
Quadrupelpunkt und Tripelpunkt

6 Beim Dreieck

Wir arbeiten mit einem beliebigen unregelmäßigen Dreieck.

Entgegengesetzt gleiches Drehen von zwei Geraden durch zwei Dreiecksecken führt zunächst zur Mittelsenkrechte einer Seite und zu einem dieser Seite angesetzten gleichschenkligen Dreieck.

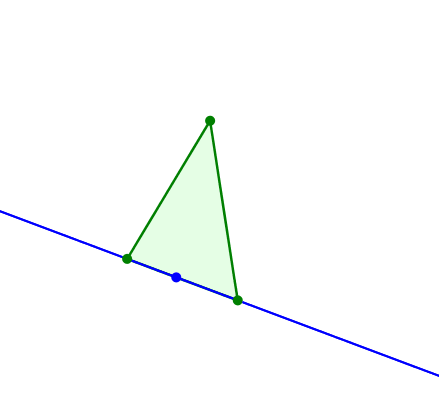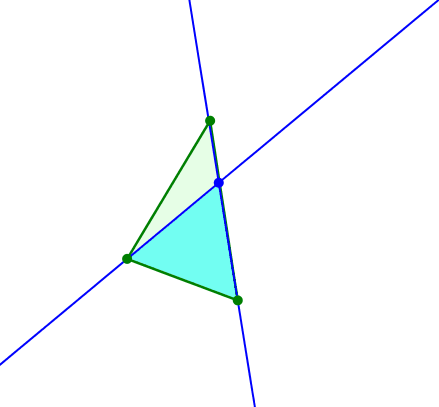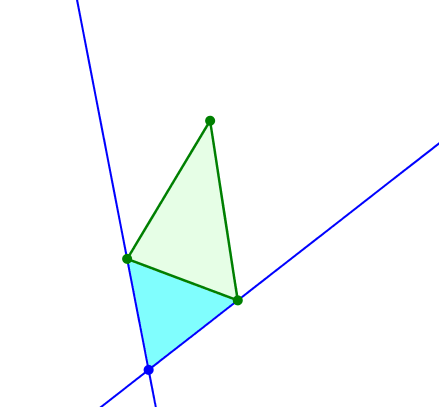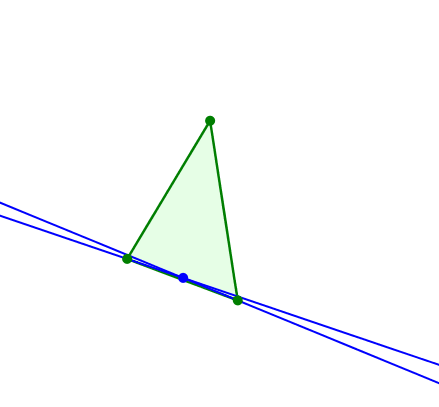
Gleichschenkliges Dreieck

Wir können allen drei Dreiecksseiten gleichschenklige Dreiecke ansetzen. Bei synchronem Drehen sind die gleichschenkligen Dreiecke ähnlich.

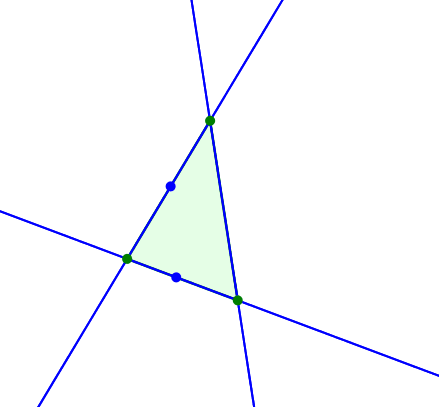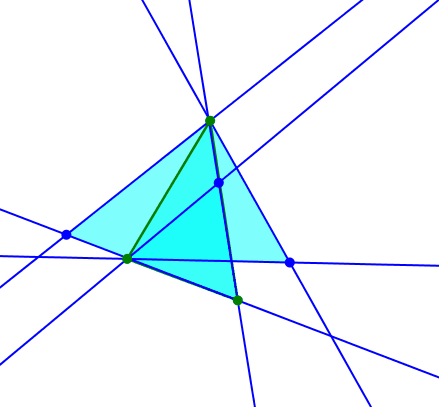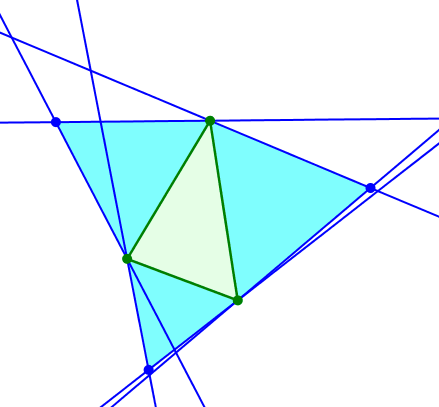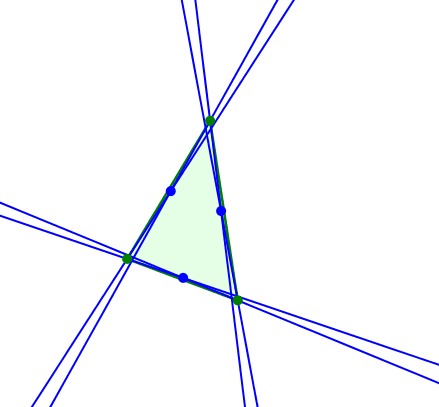
Ähnliche gleichschenklige Dreiecke

Bei sehr kleinen Basiswinkeln werden in der Verlängerung der Schenkel weitere Schnittpunkte sichtbar.

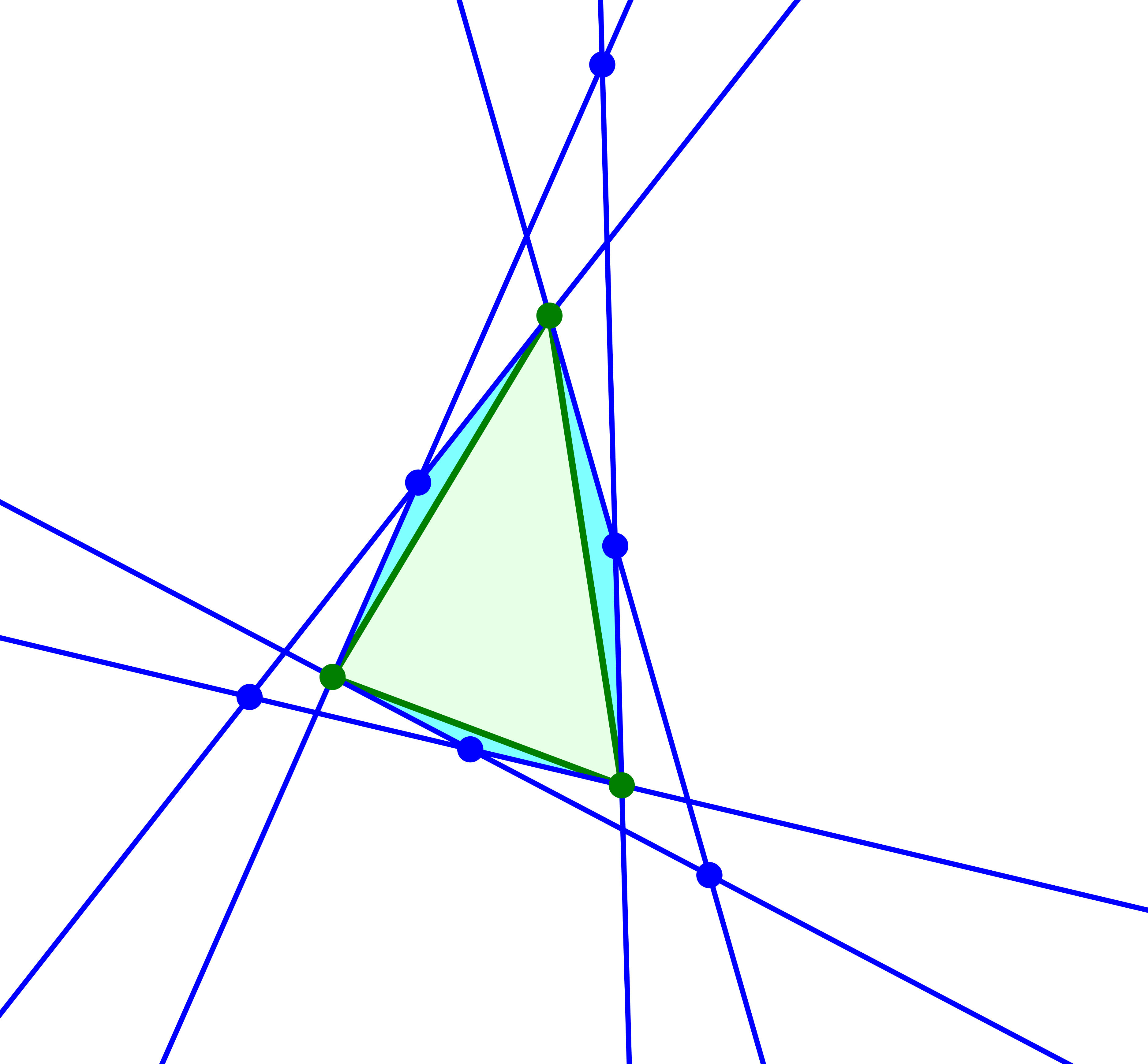
Weitere Schnittpunkte

7 Merkwürdige Punkte

Wenn in der Dreiecksgeometrie drei Geraden durch denselben Punkt verlaufen, spricht man von einem „merkwürdigen Punkt“. Klassische Beispiele sind die drei Höhen, die drei Schwerlinien, die drei Winkelhalbierenden und die drei Mittelsenrechten der Seiten. Es gibt aber viele weitere merkwürdige Punkte im Dreieck (Walser 2006, Walser 2012, sowie hier).

In unserem Kontext werden wir drei Beispiele von merkwürdigen Punkten antreffen.

Erster merkwürdiger Punkt: Werden die grünen Ecken des Startdreiecks mit den blauen Spitzen der gegenüberliegenden gleichschenkligen Dreieck verbunden, erhalten wir einen merkwürdigen Punkt, der als Kiepert-Punkt bezeichnet werden kann (Erklärung der Bezeichnung folgt).

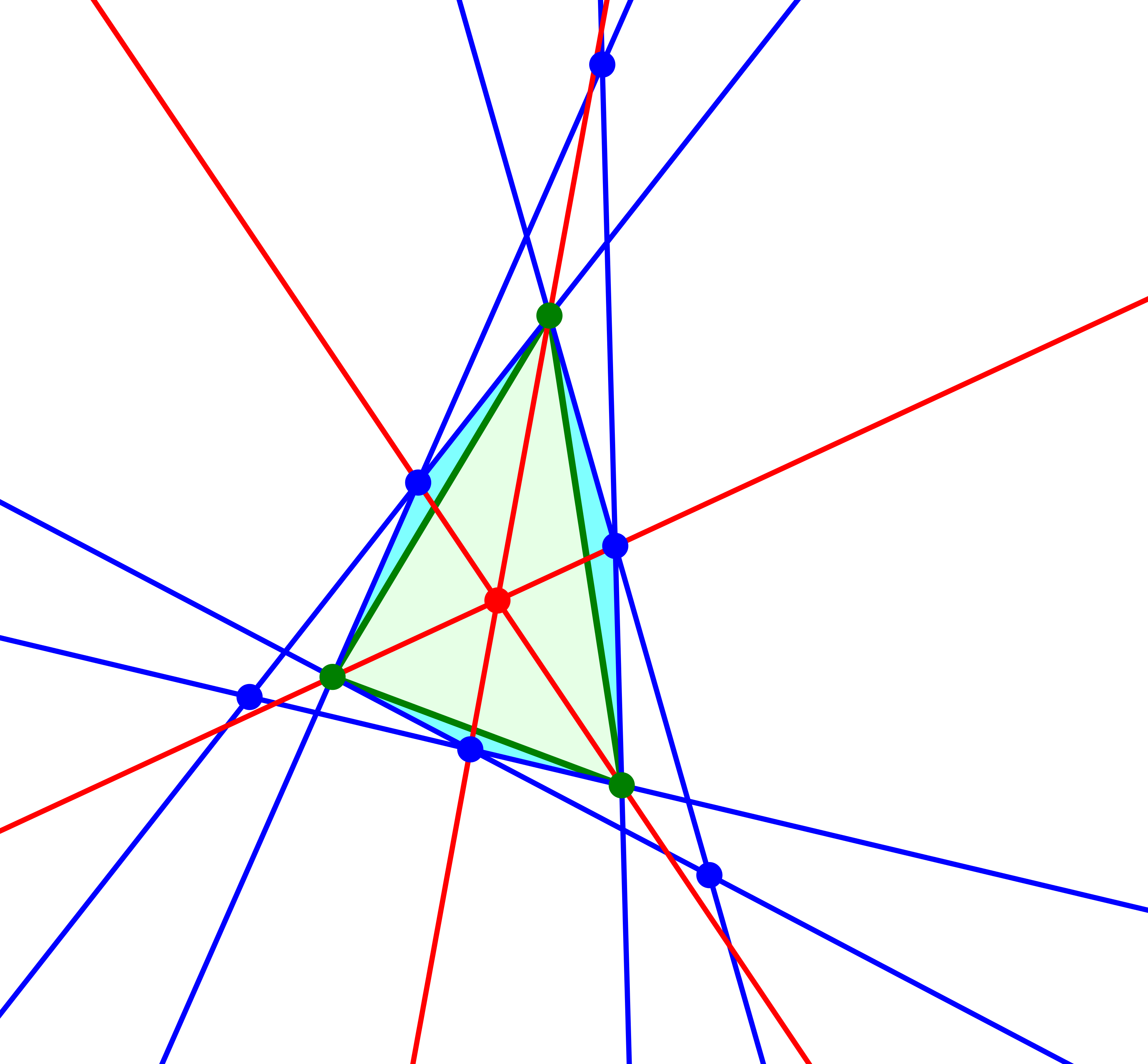
Ein Bild, das Beitrag, farbig, Laser enthält.

Automatisch generierte Beschreibung

Kiepert-Punkt

Zweiter merkwürdiger Punkt: Wir können die grünen Dreiecksecken auch mit den rückwärtigen blauen Schnittpunkten verbinden. Dadurch entsteht ein anderer merkwürdiger Punkt, sozusagen ein zweiter Kiepert-Punkt.

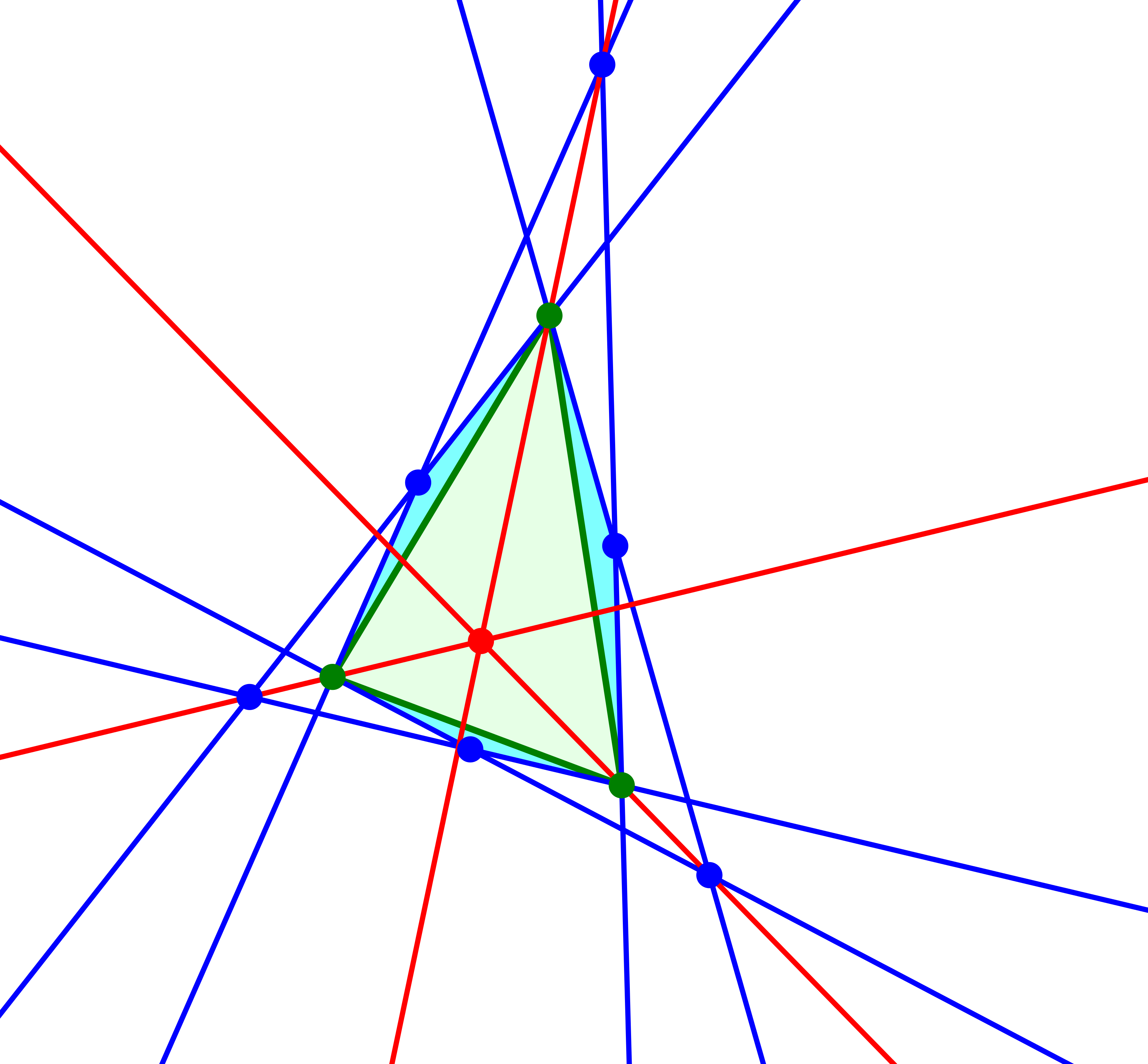
Ein Bild, das Beitrag, Laser, farbig enthält.

Automatisch generierte Beschreibung

Zweiter Kiepert-Punkt

Dritter merkwürdiger Punkt: Schließlich können wir die rückwärtigen blauen Punkte mit den gegenüberliegenden blauen Spitzen der gleichschenkligen Dreiecke verbinden. So entsteht ein weiterer merkwürdiger Punkt. Es wird sich zeigen, dass man ihn sinnvollerweise als Euler-Punkt bezeichnet.

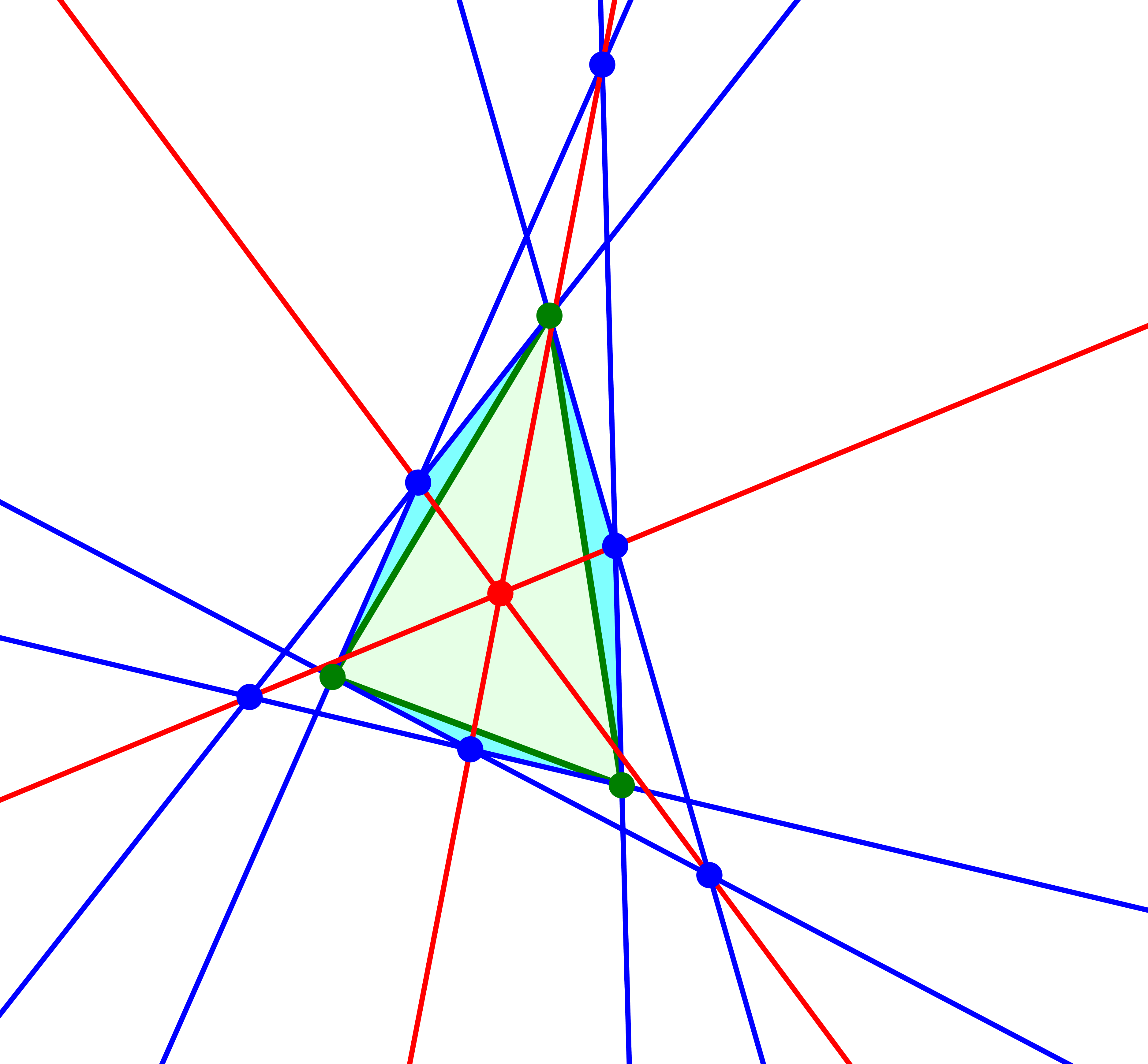
Ein Bild, das draußen, farbig, Beitrag, Laser enthält.

Automatisch generierte Beschreibung

Euler-Punkt

8 Bewegte merkwürdige Punkte

Werden nun die blauen Geraden gedreht, bewegen sich unsere drei merkwürdigen Punkte. Was für Bahnkurven entstehen?

8.1 Kiepert-Hyperbel

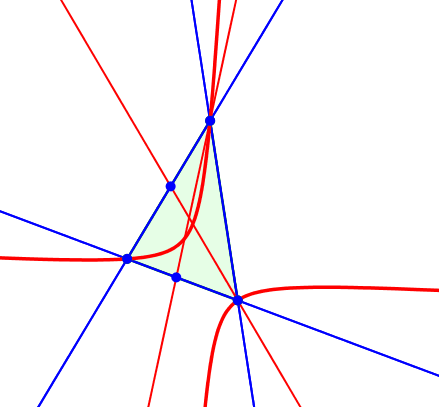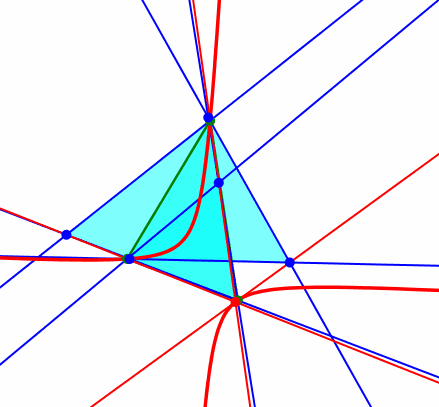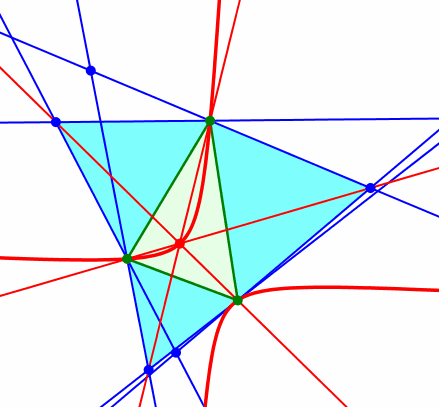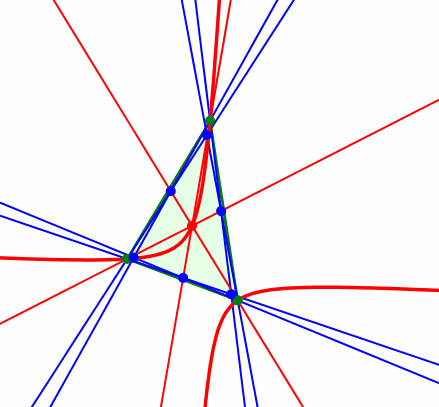
Erster merkwürdiger Punkt: Der erste Kiepert-Punkt bewegt sich auf einer gleichseitigen Hyperbel, der sogenannten Kiepert-Hyperbel. Diese Hyperbel geht zurück auf Friedrich Wilhelm August Ludwig Kiepert (1846-1934). Kiepert war ein Gründungsmitglied der Deutschen Mathematiker-Vereinigung DMV.

Kiepert-Hyperbel

Die Kiepert-Hyperbel verläuft durch die drei Dreiecksecken. Die Seite mit mittlerer Länge ist Sehne in einem Hyperbelast. Weiter verläuft die Kiepert-Hyperbel durch den Höhenschnittpunkt und den Schwerpunkt des Startdreieckes. Damit ist die Kiepert-Hyperbel als Kegelschnitt festgelegt (fünf definierende Punkte).

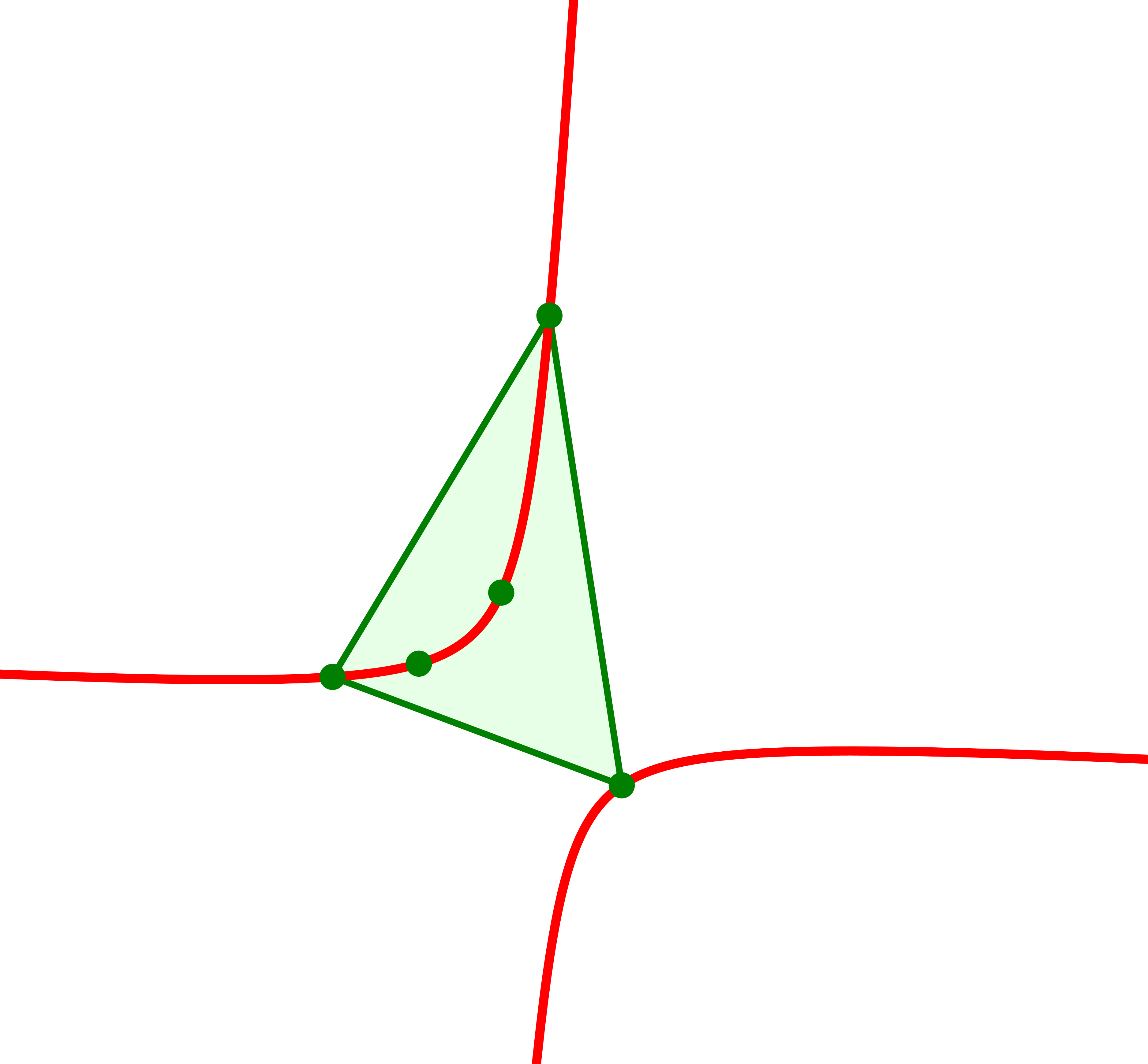
Kiepert-Hyperbel durch fünf Punkte festgelegt

Die Kiepert-Hyperbel enthält aber auch zum Beispiel den Fermat-Punkt. Dieser ergibt sich im Sonderfall von angesetzten gleichseitigen Dreiecken. Der Fermat-Punkt ist der Verzweigungspunkt für das Wegenetz minimaler Länge, das die drei Dreiecksecken verbindet.

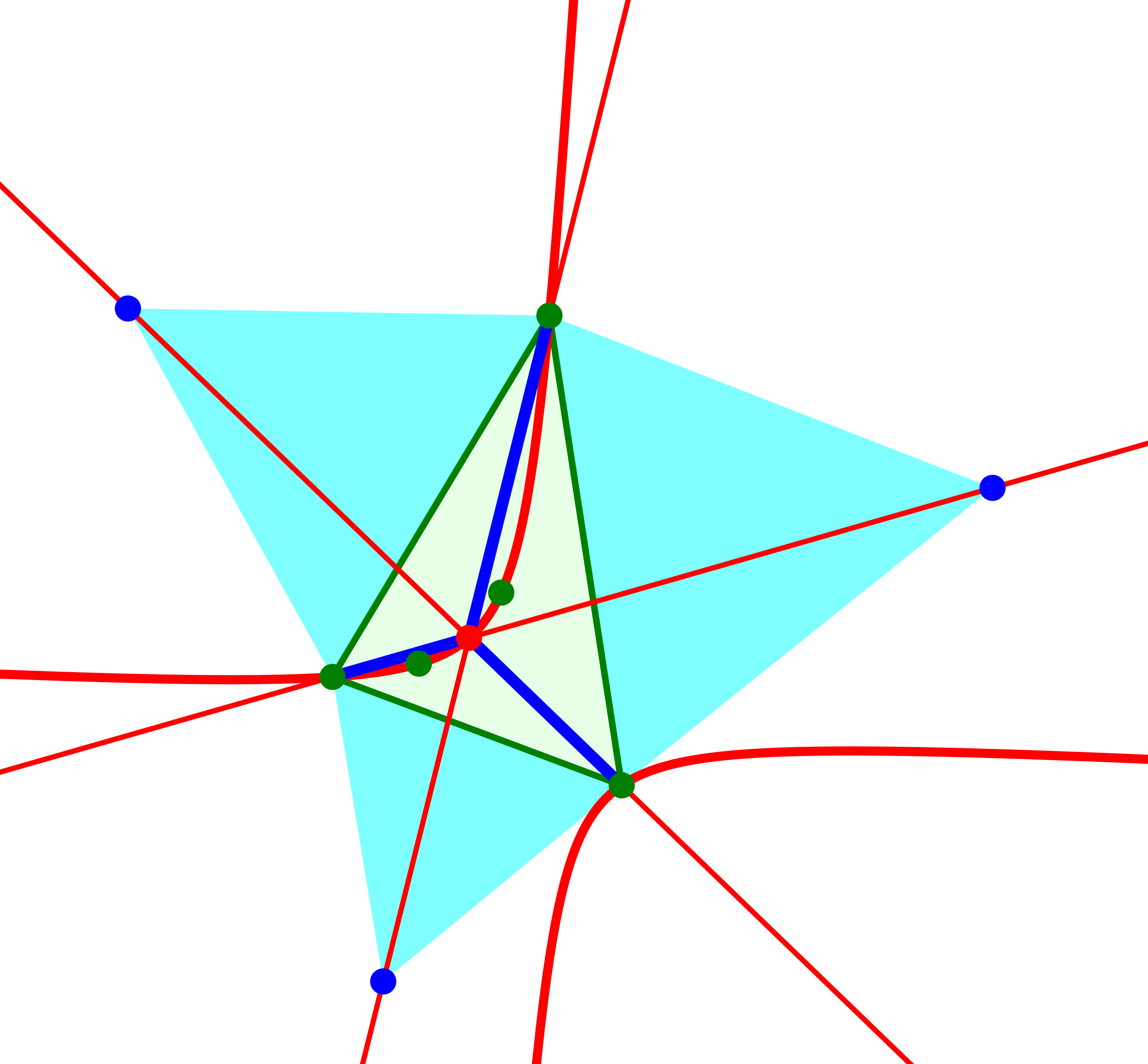
Kiepert-Hyperbel

8.2 Kiepert-Gerade

Zweiter merkwürdiger Punkt: Wer jetzt beim zweiten Kiepert-Punkt ebenfalls einen Kegelschnitt als Bahnkurve erwartet, wird freudig enttäuscht. Die Bahnkurve ist eine Gerade, die Kiepert-Gerade.

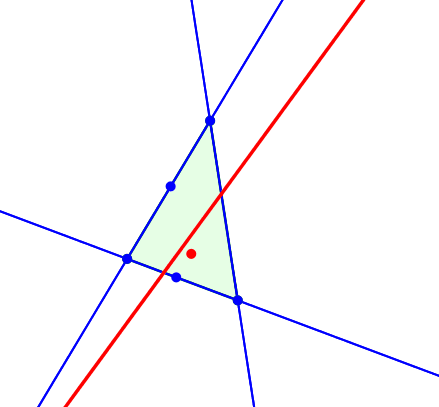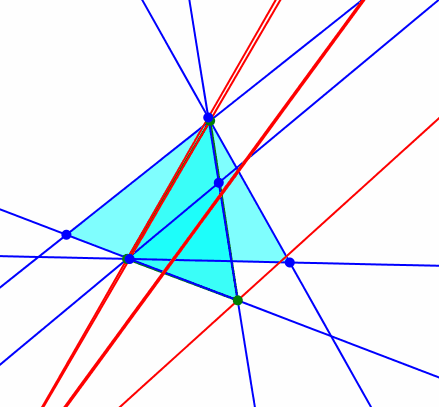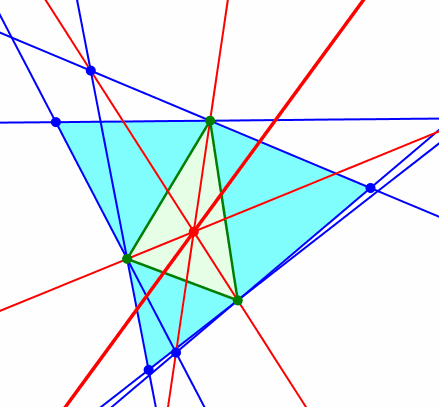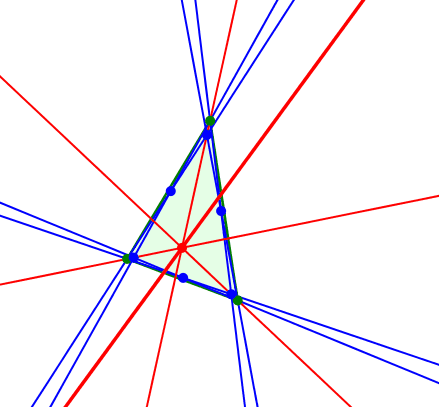
Kiepert-Gerade

Die Kiepert-Gerade verläuft durch den Umkreismittelpunkt des Startdreieckes.

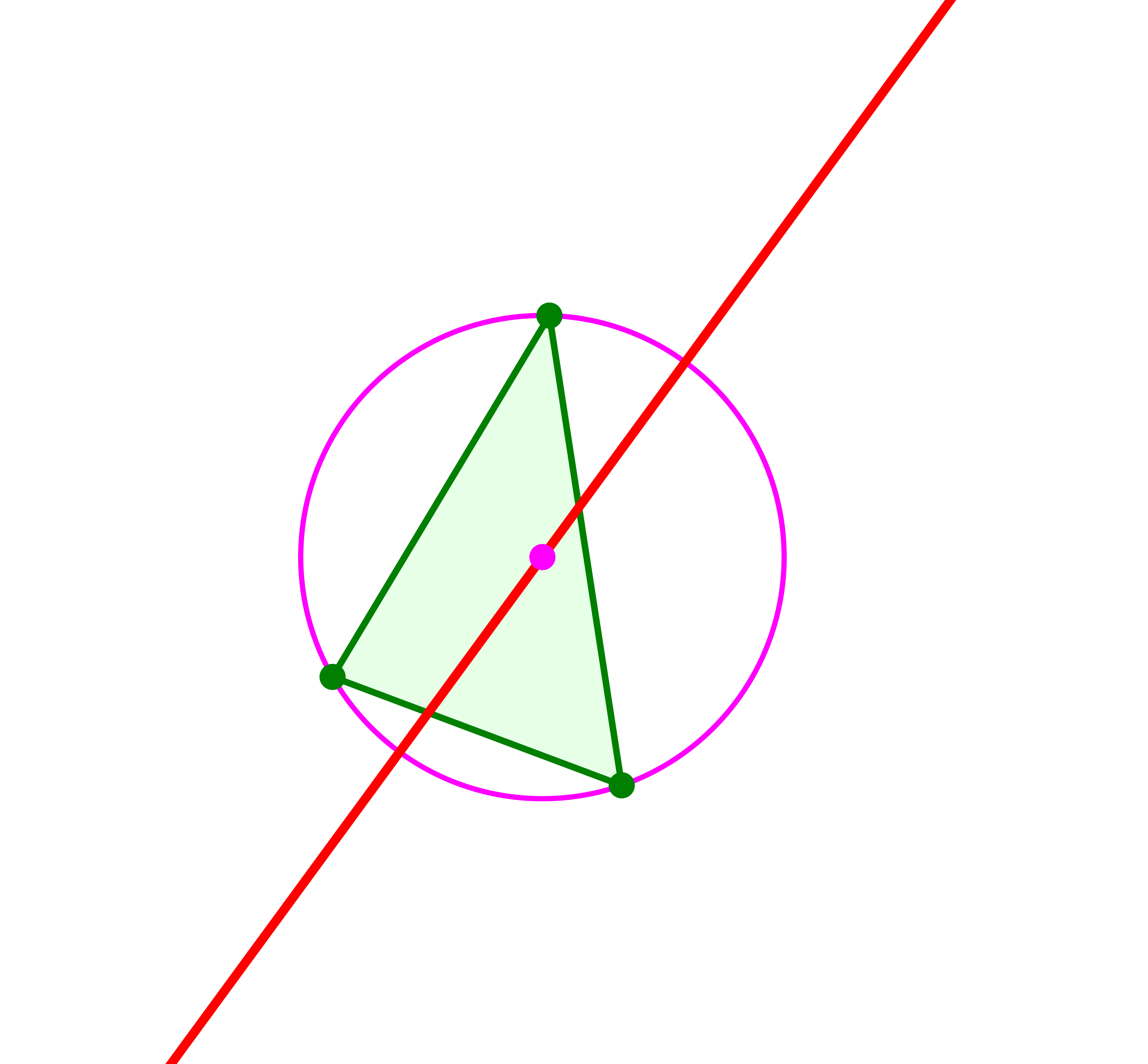
Ein Bild, das Laser enthält.

Automatisch generierte Beschreibung

Kiepert-Gerade und Umkreismittelpunkt

8.3 Euler-Gerade

Dritter merkwürdiger Punkt: Und nun bleibt noch der Euler-Punkt. Er bewegt sich auf der Euler-Geraden.

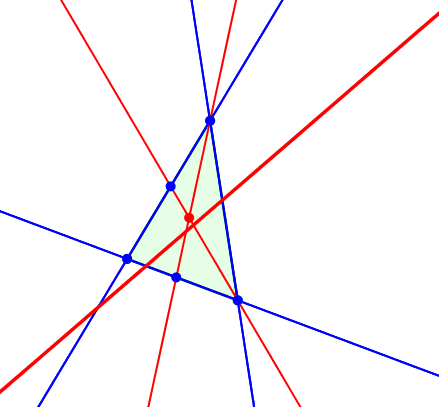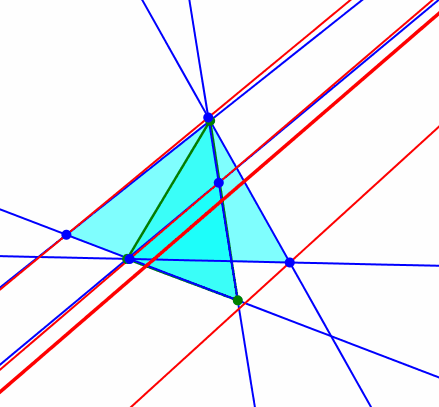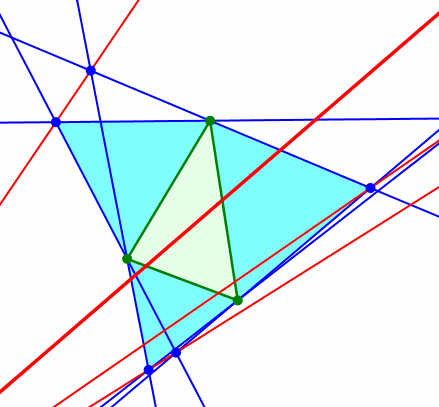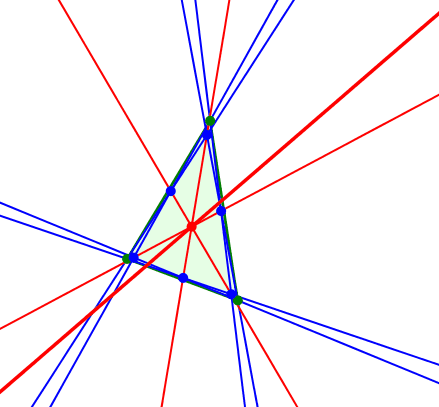
Euler-Gerade

Die Euler-Gerade verläuft durch den Höhenschnittpunkt, den Schwerpunkt und den Umkreismittelpunkt des Startdreieckes. Zudem ist noch der Spiegelpunkt des Höhenschnittpunktes bei Spiegelung am Umkreismittelpunkt eingetragen. Den Grund dazu werden wir gleich einsehen.

Ein Bild, das Laser enthält.

Automatisch generierte Beschreibung

Euler-Gerade

Wenn wir nämlich die Bewegung des Euler-Punktes auf der Euler-Geraden aufmerksam verfolgen, sehen wir zwei Umkehrpunkte, nämlich den Schwerpunkt und den Spiegelpunkt des Höhenschnittpunktes bei Spiegelung am Umkreismittelpunkt. Das Stück dazwischen wird vom Euler-Punkt nicht bestrichen.

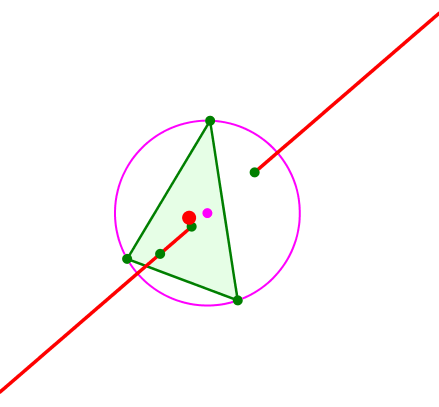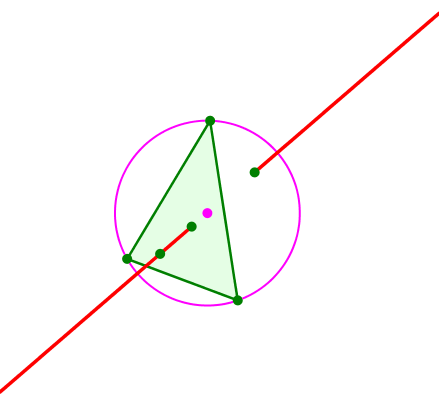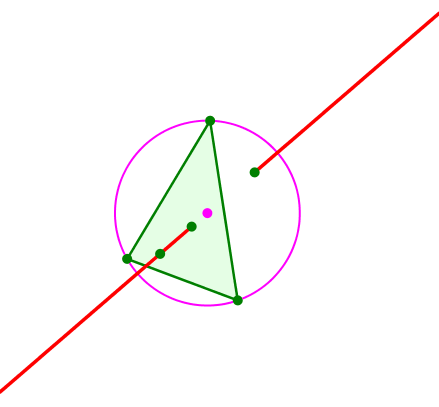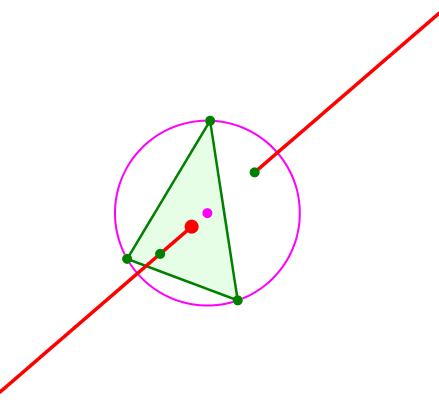
Umkehrpunkte

8.4 Übersicht

Da haben wir also die Kiepert-Hyperbel, die Kiepert-Gerade und die Euler-Gerade.

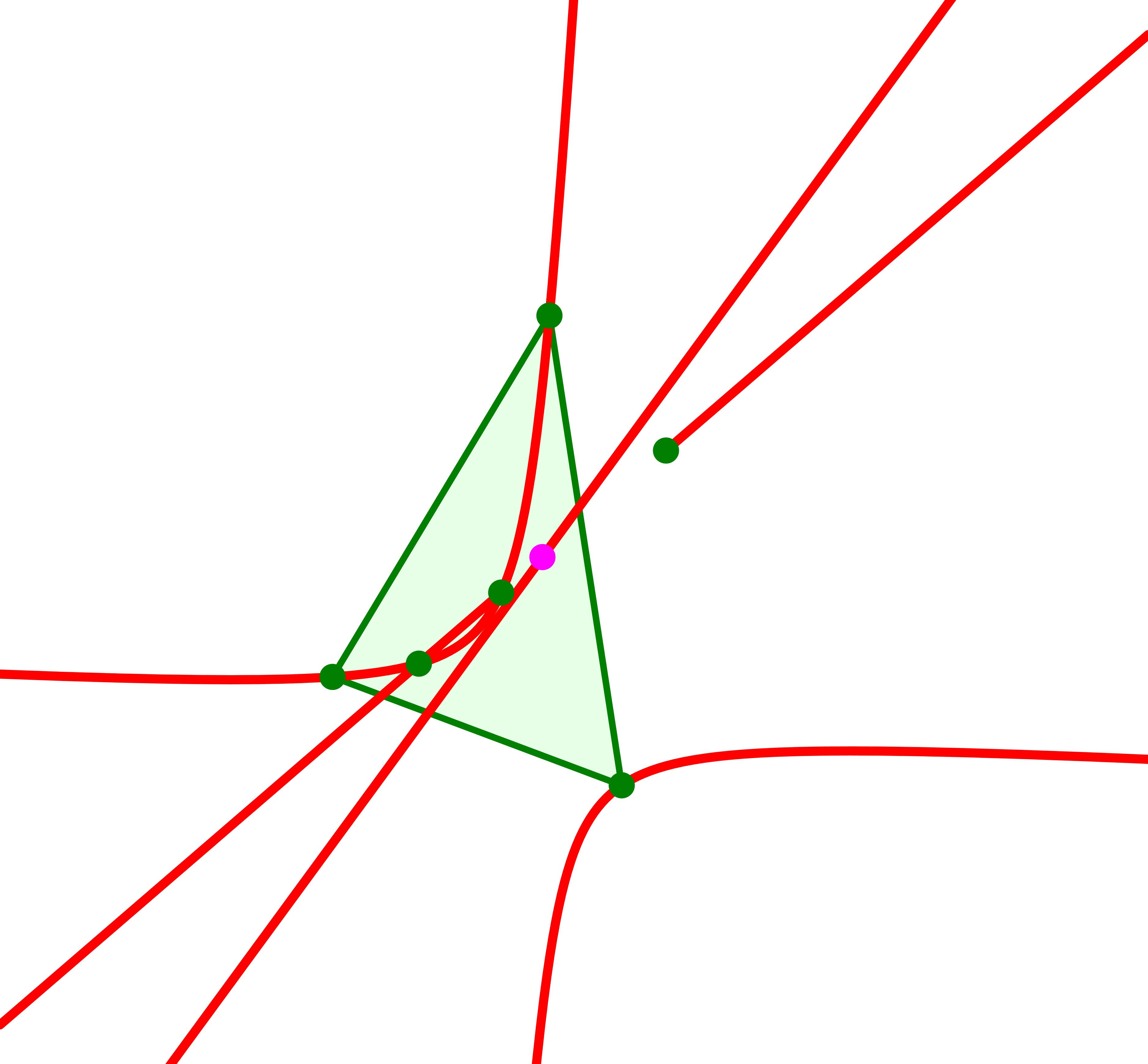
Ein Bild, das Laser enthält.

Automatisch generierte Beschreibung

Die drei Bahnkurven

8.5 Bewegte merkwürdige Gerade

Wenn wir die generierenden merkwürdigen Punkte mit eintragen, vermuten wir bei raschem Blick eine merkwürdige Gerade.

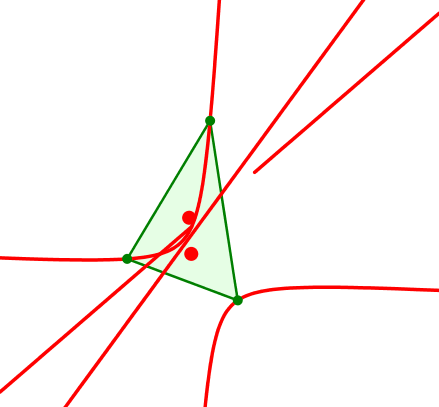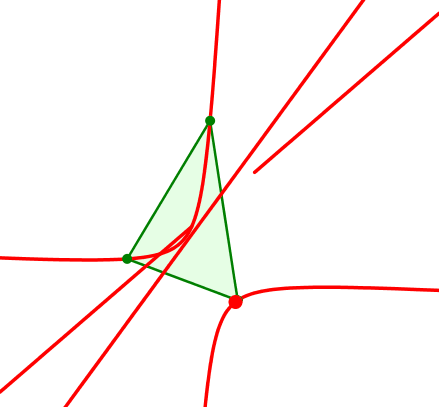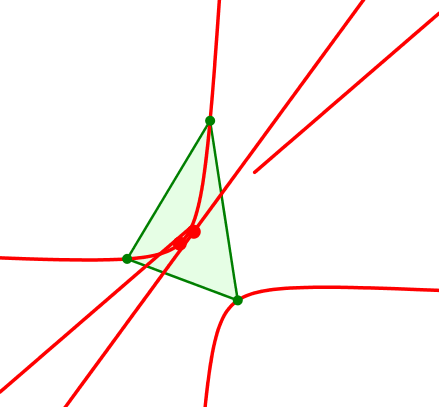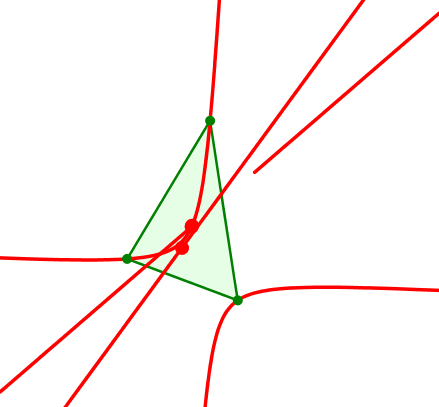
Generierende merkwürdige Punkte

Die drei generierenden merkwürdigen Punkte, also die beiden Kiepert-Punkte und der Euler-Punkt, liegen auf einer Geraden.

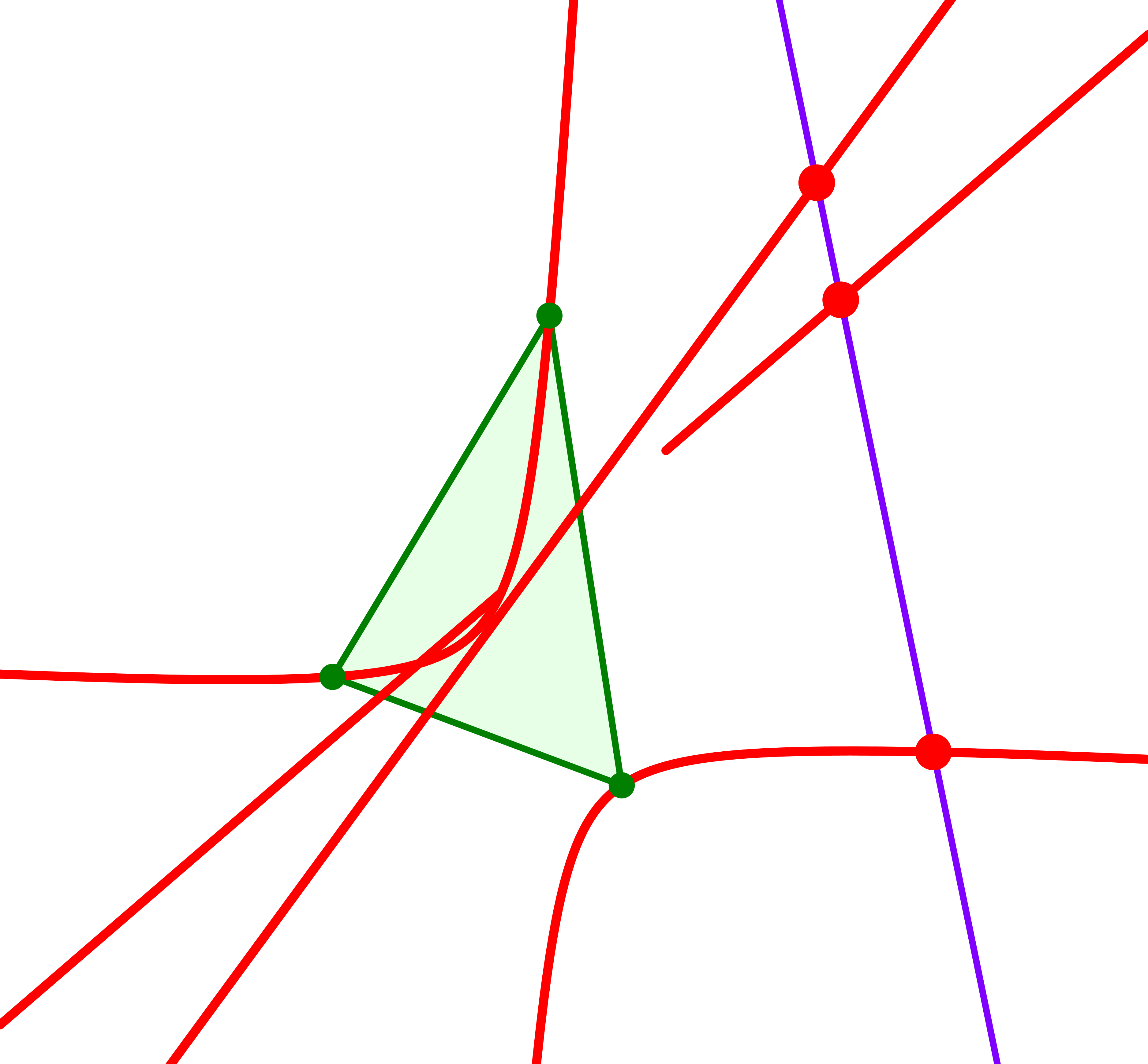
Merkwürdige Punkte auf einer merkwürdigen Geraden

Auch diese Gerade wird bewegt.

Bewegte merkwürdige Gerade

9 Der gedrehte Punkt

Abrollendes Rad: Zykloide

Im Mathematikum zu Gießen gibt es als Exponat zum Anfassen ein schönes Holzmodell der Zykloide mit dem dazugehörenden abrollbaren Rad. Ein am Rand des Rades befestigter Stift fährt dann das Zykloidenprofil ab.

Bei einem Besuch im Mathematikum wurde ich Zeuge folgender Szene: Ein Besucher zeigte seiner Begleiterin, wie der Stift den Zykloidenbogen abfährt. Er fuhr sogar selber mit dem Finger den Bogen ab. Das sei also der Weg eines Kreispunktes bei einer Umdrehung, mithin der Umfang des Kreises.

Ich war perplex. Mussten wir doch als junge Student*innen die Länge eines Zykloidenbogens berechnen und es kam 8r (r = Radradius) heraus und der Assistent sagte, dieses Resultat gehe auf Christopher Wren (1632-1723) zurück und es sei ein erstes Beispiel der Anwendung der Differential- und Integralrechnung gewesen.

Als ich wieder zu mir kam, waren der Besucher und seine Begleiterin verschwunden, so dass ich sie nicht mehr belehren konnte.

Aber: Was ist eigentlich falsch an der Vorstellung, der Umfang des Kreises sei der zurückgelegte Weg bei einer Umdrehung? — In der Schuldefinition des Kreisumfanges wird stillschweigend angenommen, dass das Rad sich zwar dreht, aber nicht rollt. Eine sehr fragwürdige Definition. Als Didaktiker ist man versucht den vom sinnstiftenden Unterricht zu zitieren und als Praktiker montiert man die Schneeketten.

Wenn allerdings ein Kameramann gleichauf neben dem rollenden Rad herrennt, erscheint auf dem Film ein Rad, das dreht, aber nicht rollt.

Das Rad dreht, rollt aber nicht

Wenn umgekehrt das Rad zwar dreht, aber nicht rollt, hingegen der Kameramann zur Seite rennt, erscheint auf dem Film eine bewegte Zykloide.

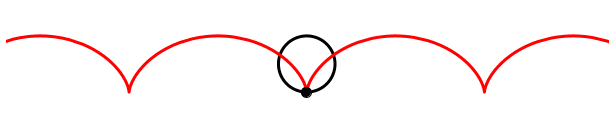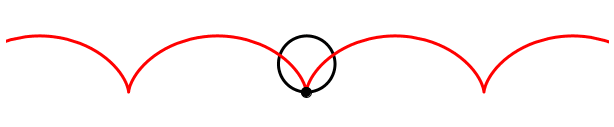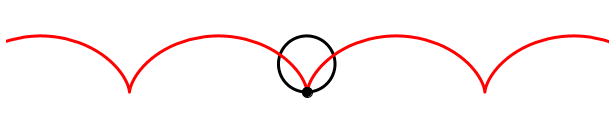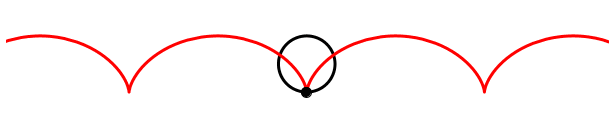
Ein Bild, das Sport enthält.

Automatisch generierte Beschreibung

Bewegte Zykloide

Was sieht man auf dem Film, wenn der Kameramann in der Gegenrichtung rennt? — Die Zykloidenspitzen weisen nach oben.

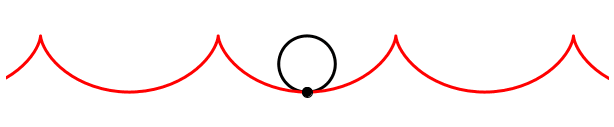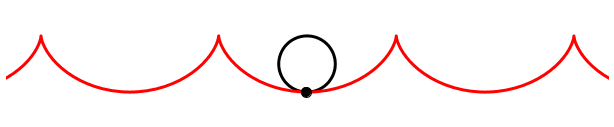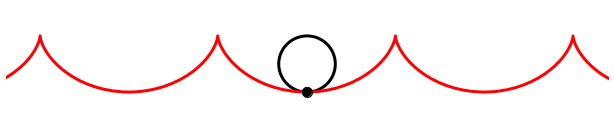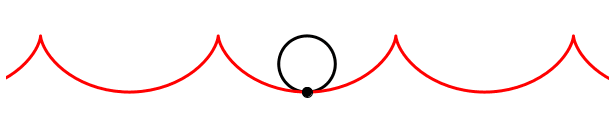
Gegenrichtung

10 Rosette

Und wenn der Kameramann seine Kamera dreht? — Der Punkt bewegt sich auf einer drehenden Rosette.

Gedrehte Kamera

Überlagerung der drei Filme

Die rote Rosette und der schwarze Kreis haben denselben Flächeninhalt. Die Rosette hat (im Stillstand) die Polargleichung:

11 Rosettengetriebe

Wir beginnen mit dem sich auf einem Kreis drehenden Punkt, der die Rosette mit drei Blütenblättern antreibt.

Der Punkt treibt die Rosette an

Die Rosette ihrerseits treibt einen Propeller an. Dieser dreht allerdings nur halb so schnell wie der Punkt.

Propeller

Und der Propeller treibt eine weitere Rosette an. Diese ist blau und hat fünf Blütenblätter.

Noch eine Rosette

Die blaue Rosette ihrerseits treibt ein gleichseitiges Dreieck um.

Gleichseitiges Dreieck

Der*die geneigte Leser*in ahnt, wie es weitergeht.

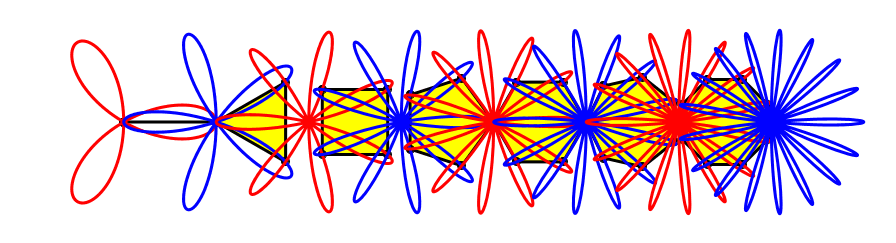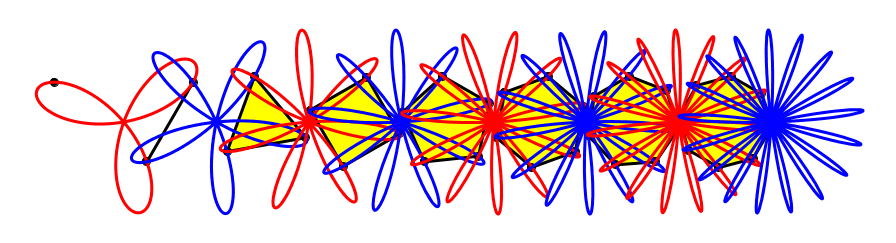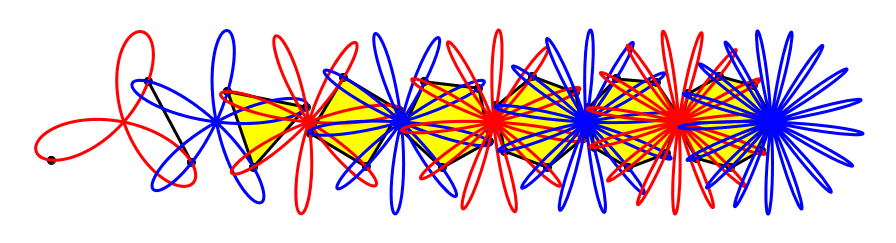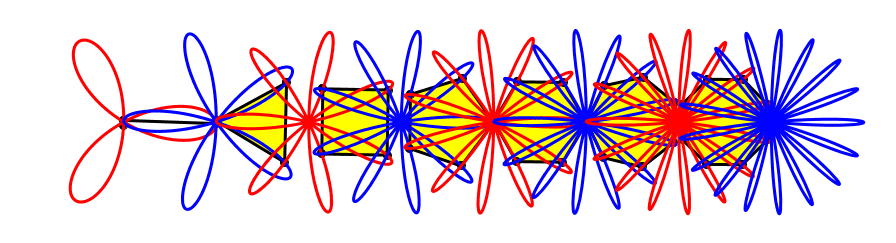
Rosettengetriebe

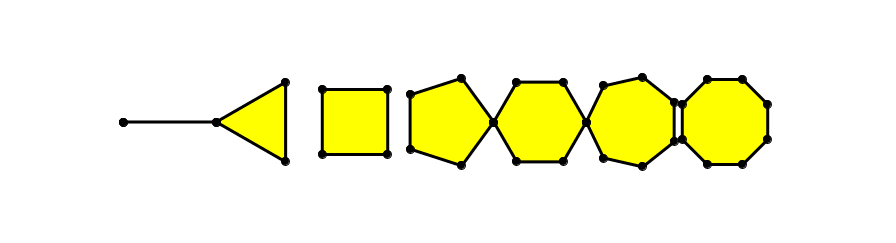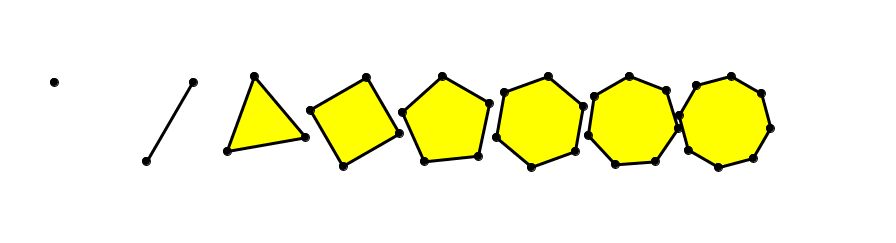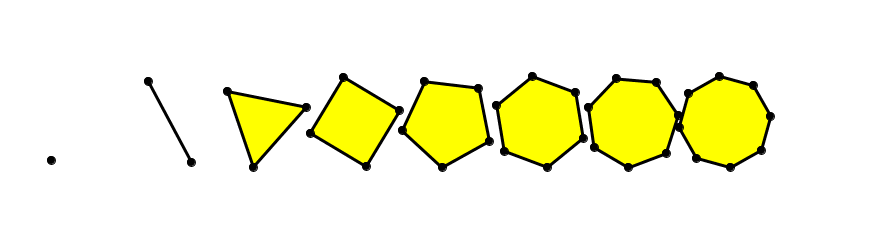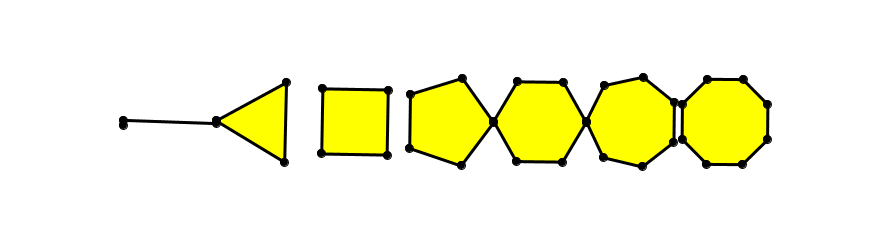
Regelmäßige Vielecke, angefangen beim Eineck

Die Drehgeschwindigkeiten der umgetriebenen regelmäßigen Vielecke bilden eine abnehmende harmonische Folge:

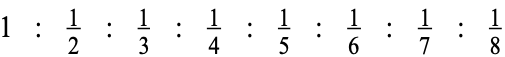
Harmonische Folge

Wenn das so weitergeht, erhalten wir am Schluss einen stillstehenden Kreis. Damit sind wir am Ende der bewegten Geometrie.

Literatur

Eddy, R.H. / Fritsch, R. (1994): The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June 1994, p. 188-205.

Walser, Hans (1993): Die Eulersche Gerade als Ort "merkwürdiger Punkte". Didaktik der Mathematik (21), S. 95-98.

Walser, Hans (2006): 99 Points of Intersection. Examples – Pictures – Proofs. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America. ISBN 0-88385-553-4

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0.

Websites

Mathematikum Gießen

https://www.mathematikum.de

Hans Walser: Achterschleife

http://www.walser-h-m.ch/hans/Miniaturen/A/Achterschleife/Achterschleife.html

Hans Walser: Die vivianische Kurve in stereographischer Projektion – die Strophoide

http://www.walser-h-m.ch/hans/Miniaturen/V/Viviani/Viviani.htm

Hans Walser: Drehgeraden

http://www.walser-h-m.ch/hans/Miniaturen/D/Drehgeraden/Drehgeraden.html

Hans Walser: Eulergerade

http://www.walser-h-m.ch/hans/Miniaturen/E/Eulergerade4/Eulergerade4.html