Hans Walser
Invariante Flächensummen
Österreichische Fortbildungstagung für Geometrie
9.-11. November 2023
BIFEB, Bundesinstitut für Erwachsenenbildung
Strobl am Wolfgangsee
Abstract
Einige geometrische Sätze, insbesondere der Satz des Pythagoras, werden unter dem Aspekt der invarianten Flächensumme untersucht. Diese neue Sichtweise ermöglicht ein ganzes Feld von Verallgemeinerungen und zugehörigen Illustrationen.
Inhalt
4 Als ich das erste Mal auf dem Dampfwagen saß
5 Achterbahn (Lissajous-Kurve)
12 Einfachstes Beispiel: Apollonios / al Sijzi
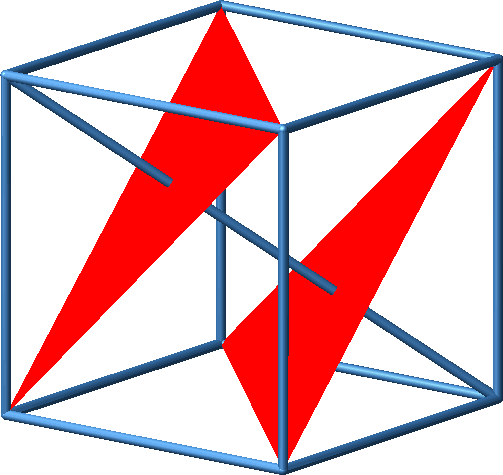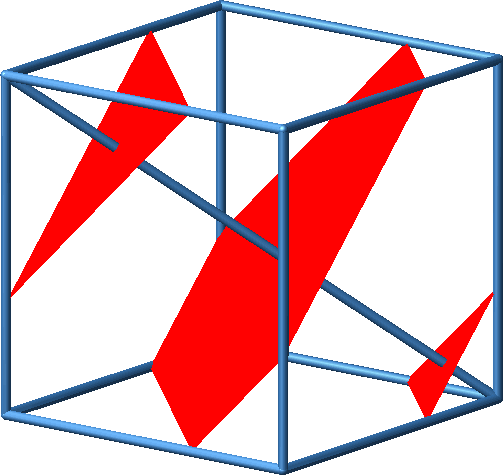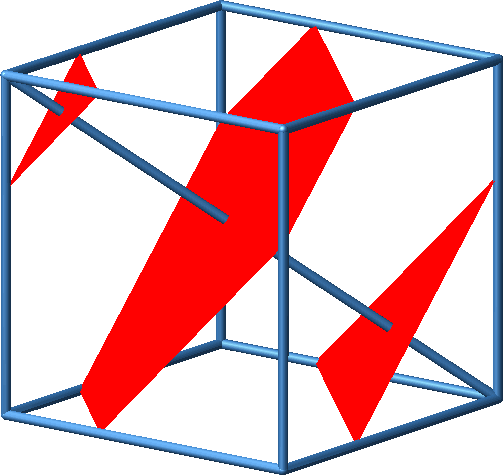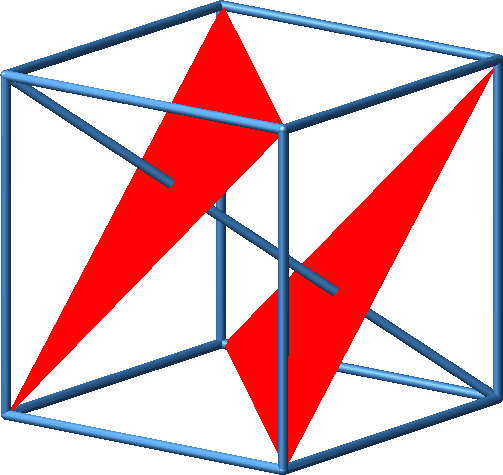
1 Würfelschnitte
In ein Kantenmodell eines Würfels tragen wir eine Raumdiagonale ein. Nun schneiden wir den Würfel mit Ebenen, welche zur Raumdiagonale senkrecht stehen. Die Ebenen haben untereinander gleiche Abstände, nämlich einen Drittel der Länge der Raumdiagonale .
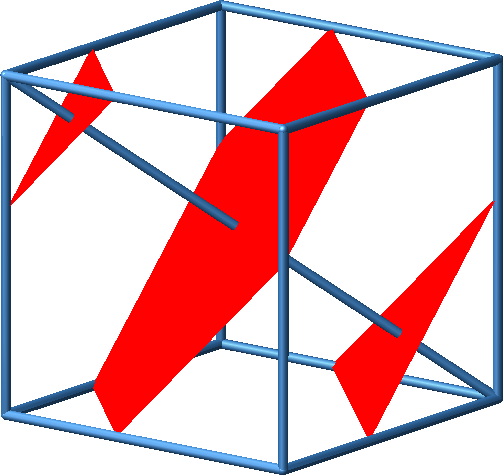
Schnitt mit parallelen Ebenen
Diese Figur ist die Minimalfigur, welche in allen drei Rissen als Quadrat erscheint.
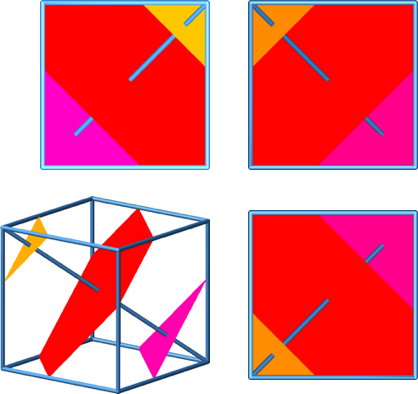
In allen drei Rissen ein Quadrat
Wenn wir Schnittebenen bewegen, ändern die Schnittfiguren Form und Größe.

Invariante Flächensumme
Ihre Flächensumme bleibt aber invariant.
Dies kann eingesehen werden, indem wir drei Würfel aufeinanderstapeln. Die drei Teilfiguren ergänzen sich zu einem Rhombus.
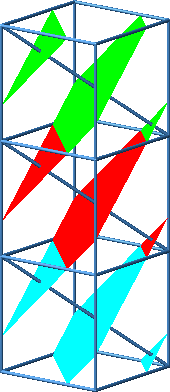
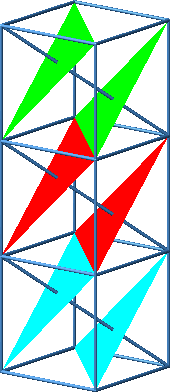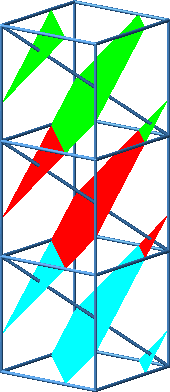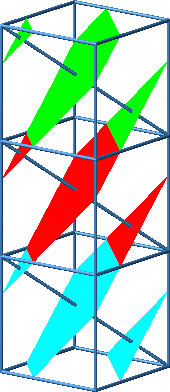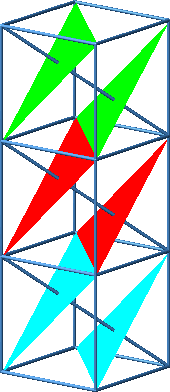
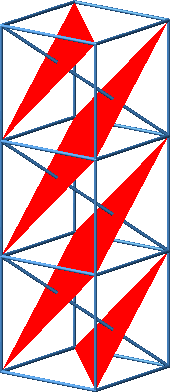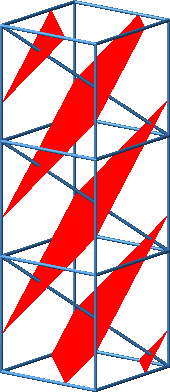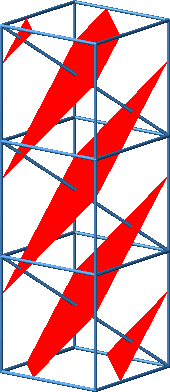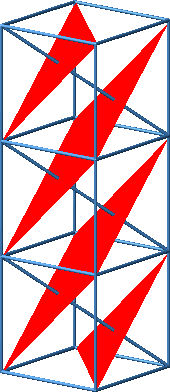
Beweisfigur
2 Invarianz bei Pythagoras
Der Witz des Satzes von Pythagoras ist nicht, wie man in der Schule ausgiebig lernt, dass a2 + b2 = c2 ist, sondern dass a2 + b2 = a2 + b2 ist, auch wenn in der Zwischenzeit der Punkt C auf dem Thaleskreis bewegt wurde. Die Invarianz der Flächensumme der beiden Kathetenquadrate also. Das c2 ergibt sich dann als Grenzfall.

Das eine gibt, das andere nimmt
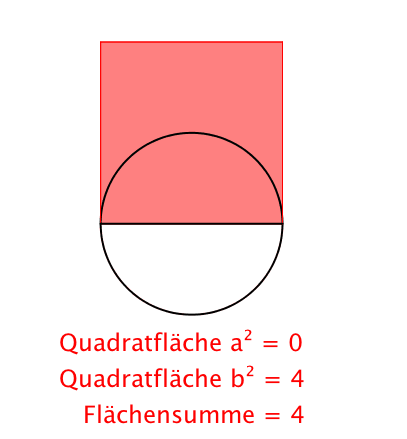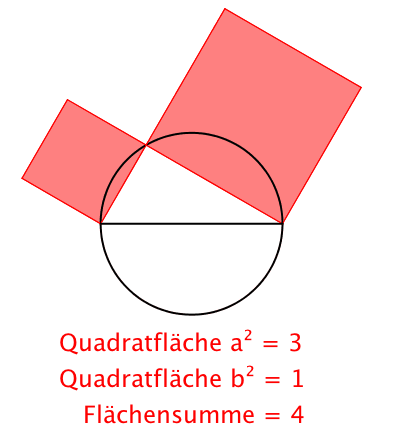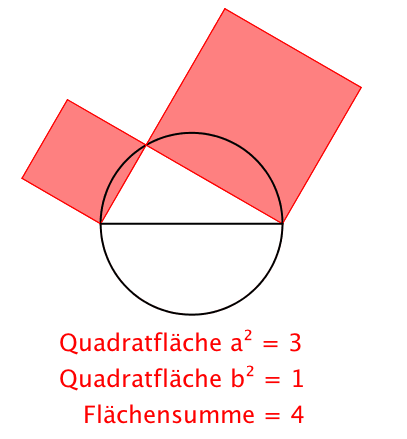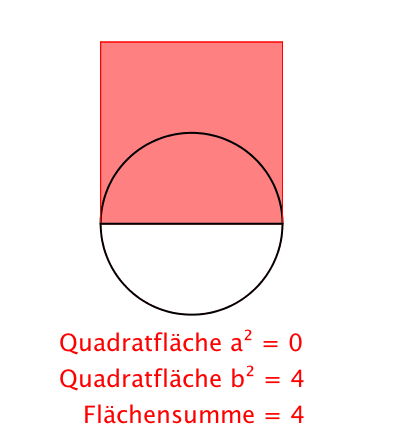
Invariante Flächensumme
3 Auf der Sinuskurve
Eine invariante Flächensumme von zwei Quadraten gibt es auch auf der Sinuskurve.

Die Fahrt auf der Sinuskurve
Die Fahrt auf der Sinuskurve
Die Länge der blau eingezeichneten Basis ist die halbe Periodenlänge.
4 Als ich das erste Mal auf dem Dampfwagen saß
Es geht auch mit fünf Quadraten.

Als ich das erste Mal auf dem Dampfwagen saß

Als ich das erste Mal auf dem Dampfwagen saß
Die blaue Basislänge ist wiederum die halbe Periodenlänge. Dass es schon mit der halben Periodenlänge geht, hat mit der Schubspiegelsymmetrie zu tun.

Schubspiegelsymmetrie
5 Achterbahn (Lissajous-Kurve)
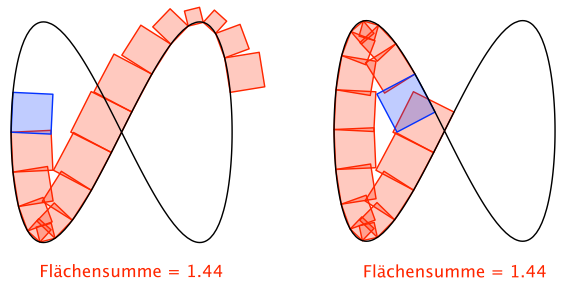
Achterbahn mit blauer Lok

Achterbahn
Die Lok schrammt knapp am letzten Wagen vorbei. Hat natürlich mit der halben Periodenlänge zu tun.

Die Lok schrammt knapp am letzten Wagen vorbei
6 Externer Pivot
Wer den Dreistern räumlich sieht und sich wundert, dass die Quadrate aufgestellt sind, ist selber schuld. Die drei bewegten Quadratecken fahren auf einer Ellipse.

Externer Pivot

Externer Pivot
Quadrate können durch Pferde ersetzt werden.

Pferde
7 Schlüsselformeln
Für den Nachweis der invarianten Flächensummen sind die folgenden Formeln hilfreich.

Sowie

Der Beweis läuft über regelmäßige n-Ecke.
Für n = 3 sind wir in der Situation des Dreiphasenstroms. Da die Spannungssumme null ist, braucht es keinen Rücklauf. Daher ist die Anzahl der Drähte bei Überlandleitungen immer ein Vielfaches von drei.

Überlandleitung
8 Der gute alte Pythagoras
In der Schule wird der Satz des Pythagoras oft mit horizontaler Hypotenuse dargestellt. Der Punkt C bewegt sich auf dem Thaleskreis. Dies entspricht dem antiken Weltbild mit einer festen horizontalen Erde (die Hypotenuse) und einer Sonne C welche bei A im Osten aufgeht, den Sonnenkreis beschreibt und dann im Westen bei B untergeht.

Klassische Darstellung
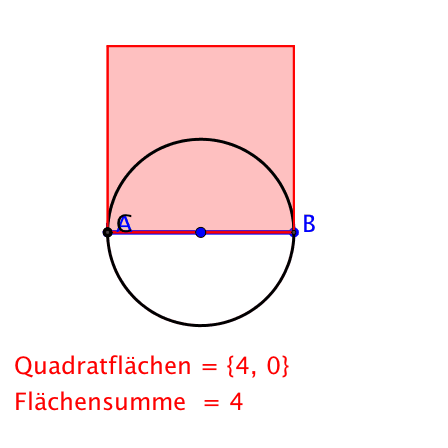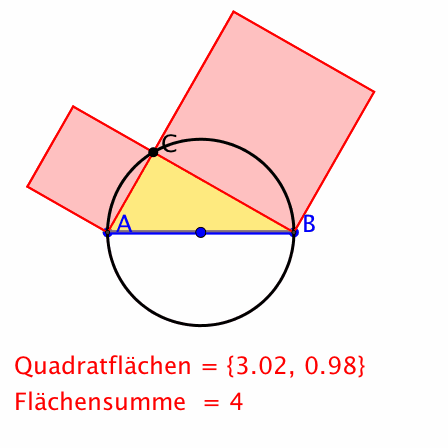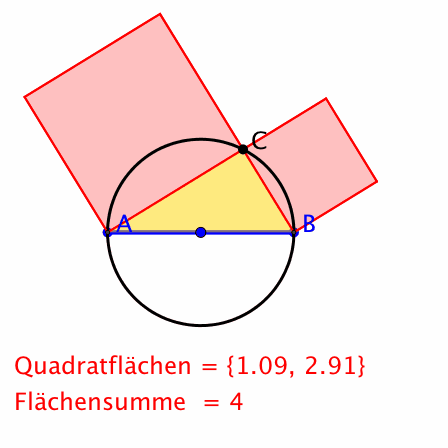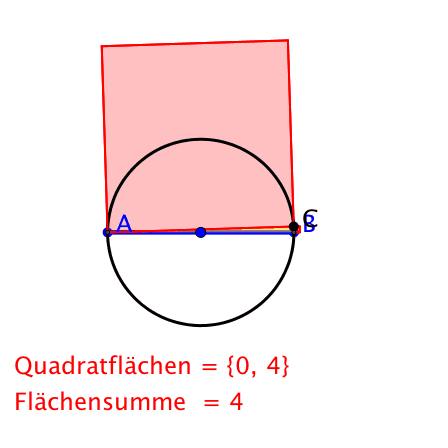
Klassische Darstellung
Nun ja, und in der Nacht geht sie untendurch zurück.
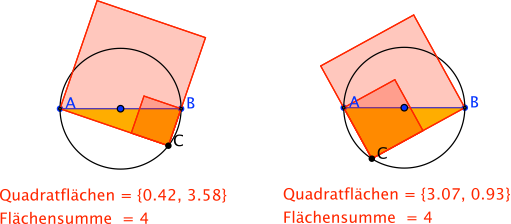
Pythagoras bei Nacht
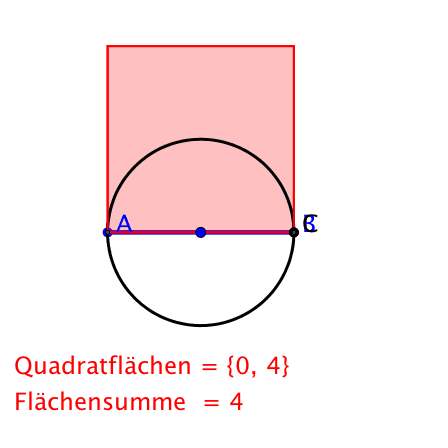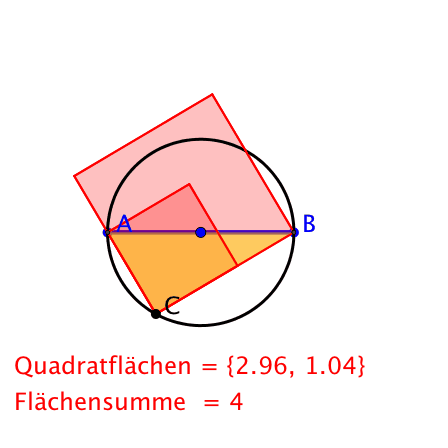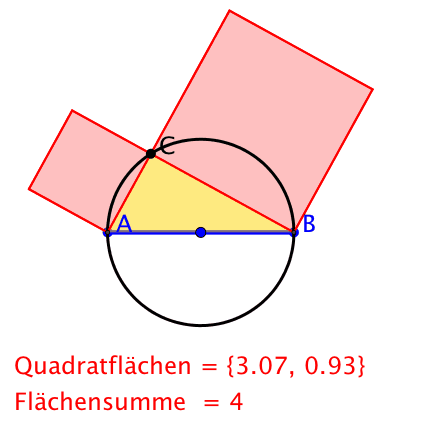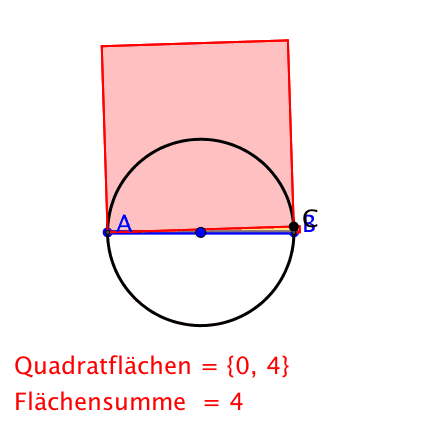
Pythagoras bei Nacht
9 Die kopernikanische Wende
Der Punkt C bleibt fest, die Hypotenuse dreht sich.
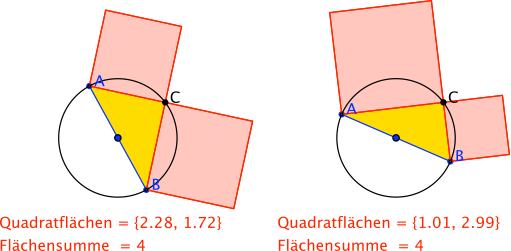
Umgekehrte Sicht. Propeller
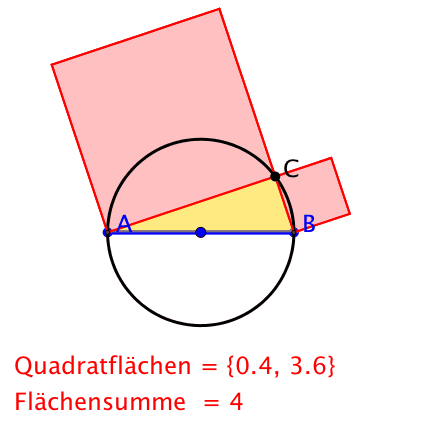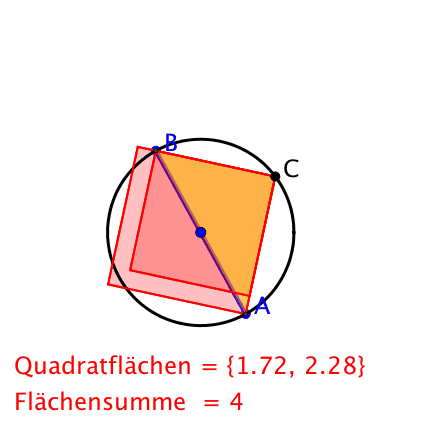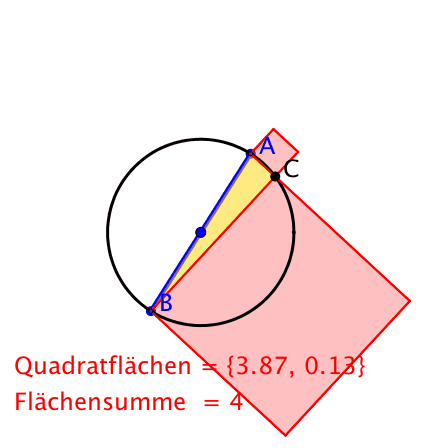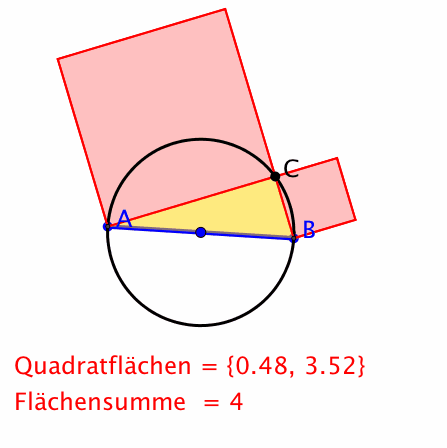
Umgekehrte Sicht. Propeller
10 Apollonios / al Sijzi
Das geht auch, wenn der Punkt C weiter weg ist (Sätze von Apollonios und al Sijzi). Wir haben dann kein rechtwinkliges Dreieck mehr.

Kein rechtwinkliges Dreieck

Kein rechtwinkliges Dreieck
Natürlich könnte man auch die Grundlinie AB festhalten und C auf einem Kreis um den Mittelpunkt der Grundlinie variieren.
11 Allgemein
Die Figur aus den Punkten A1, ... , An dreht sich um ihren Schwerpunkt S. Weiter sei C ein externer fester Punkt. Dann ist die Summe der Quadrate der Abstände von C zu den Punkten A1, ... , An invariant.
Hier ein Beispiel mit drei Punkten.

Drehen um Schwerpunkt
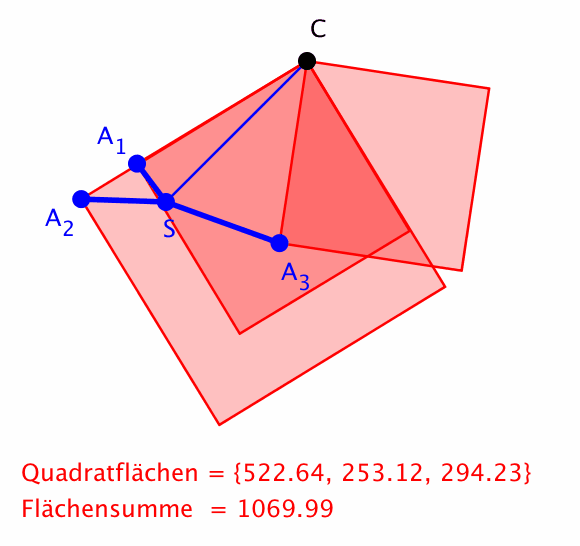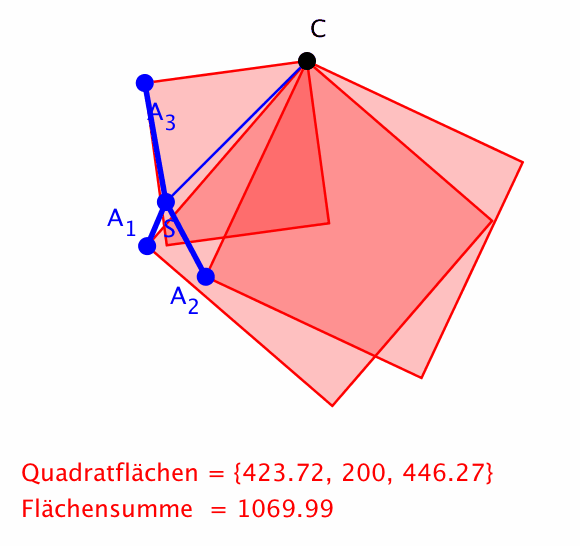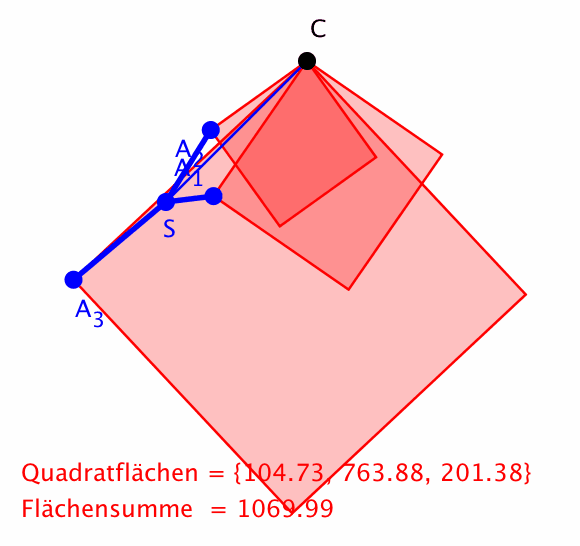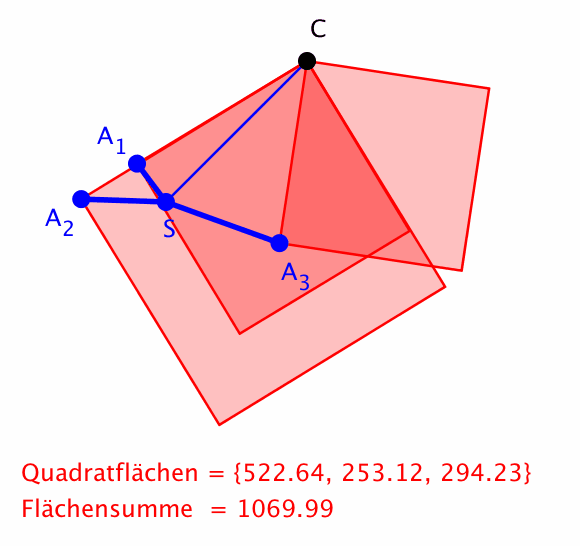
Drehen um Schwerpunkt
Beweis: Wir setzen Ak:(xk, yk), k = 1, ... , n. Den Schwerpunkt S setzen wir in den Ursprung, also S:(0, 0). Somit ist:
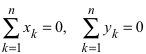
Weiter sei C:(xC, yC). Für die Summe der Quadrate der Abstände von C zu den Punkten A1, ... , An gilt:

12 Einfachstes Beispiel: Apollonios / al Sijzi
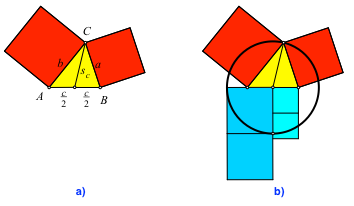
Einfachstes Beispiel. Rot = blau
Bei einem Dreieck ABC erhalten wir:
![]()
Der Sachverhalt kann visualisiert werden.
Im Sonderfall eines rechtwinkligen Dreieckes wird der blaue Teil zum Hypotenusenquadrat und wir erhalten den Satz des Pythagoras zurück.
13 Umbau der Figur
Wir zerlegen das Dreieck durch die Schwerlinie sc in zwei Teile. Diese Teile können wir in anderer Anordnung oben ansetzen. Das Dreieck kann mit einem Gelenk umgeklappt werden.
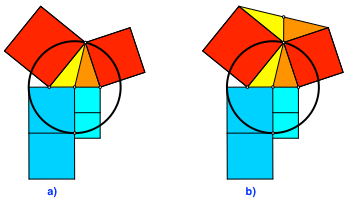
Umbau der Figur


Umklappen des Dreiecks
Nun können wir die blauen Quadrate anders anordnen.
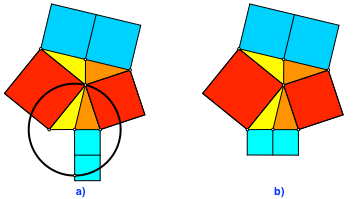
Andere Anordnung der blauen Quadrate
Schließlich bauen wir die blauen Rechtecke in Quadrate um.

Umbau der Rechtecke. Schließungsfigur
Erstaunliches geschieht. Die blauen Quadrate haben ebenfalls eine Ecke gemeinsam, wie die roten.
Auf Grund unserer Herleitung ist die Flächensumme der blauen Quadrate gleich der Flächensumme der roten.
14 Papillon
Die Figur hat einige merkwürdige Eigenschaften. Die Umkreise der vier Quadrate verlaufen durch einen gemeinsamen Punkt. Ihre Mittelpunkt, also auch die Mittelpunkte der vier Quadrate, bilden ein fünftes Quadrat.

Umkreise
Die Diagonalverbindungen der Außenecken sind orthogonal und gleich lang. Ihre Mittelpunkte sind die Kontaktpunkte gleichfarbiger Quadrate. Die Diagonalen schneiden sich im gemeinsamen Schnittpunkt der vier Umkreise. Die Diagonalverbindungen der rot-blau-Gelenkpunkte sind ebenfalls orthogonal und gleich lang und schneiden sich ebenfalls im gemeinsamen Schnittpunkt. Zu den Diagonalen der Außenecken haben sie einen Winkel 45°. Das Längenverhältnis der langen Diagonalen zu den kurzen ist die Quadratwurzel aus 2.

Diagonalen
Die folgende Abbildung zeigt die Papillon-Spirale.

Papillon-Spirale
Last modified: 21. Mai 2023
Websites
Hans Walser: Invariante Flächensummen. Vortragsseite
http://www.walser-h-m.ch/hans/Vortraege/20231109/index.html
Literatur
Walser,
Hans (2021): Spiel mit Quadraten. MU, Der Mathematikunterricht. Jahrgang 67.
Heft 3-2021. S. 17-27. ISSN 0025-5807.