Der Inkreis

Hans Walser

St. Gallen, 18. Nov. 2023

Zusammenfassung:

Mit einfachen geometrischen und mechanischen Modellen und/oder dynamischer Geometriesoftware lassen sich verschiedene klassische Berührprobleme verblüffend einfach angehen.

Zur Sprache kommen Inkreise im Dreieck und im Gelenkfünfeck, das Problem des Apollonios, Tangentenvierecke in der Ebene und im Raum, Paritätsfragen.

Letzte Bearbeitung: 19. Juli 2023

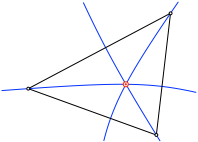
1 Inkreis im Dreieck

Der Inkreis wird mit Winkelhalbierenden konstruiert.

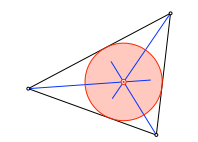
Winkelhalbierende und Inkreis

1.1 Das Damaskus-Erlebnis

Dass sich in einem Dreieck die drei Mittelsenkrechten (oder die drei Winkelhalbierenden oder die drei Höhen) in einem Punkt schneiden, hat Hans Freudenthal (1905-1990) derart getroffen, dass er sich entschloss, sein Leben der Mathematik und ihrer Didaktik zu widmen.

Hans Freudenthal (1905-1990)

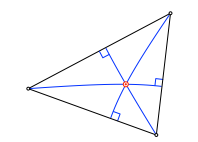
1.2 Winkelhalbierende

Der Inkreis wird in der Schule mit Winkelhalbierenden konstruiert.

Winkelhalbierende und Inkreis

Kann der Inkreis auch ohne Winkelhalbierende gefunden werden?

1.3 Kegel und Lochschablone

Wir stülpen eine Lochschablone des Dreiecks über einen geraden Kreiskegel. Am Anschlag zeigt sich der Inkreis.

Kegel und Lochschablone

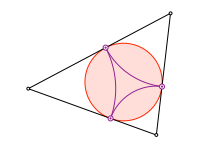
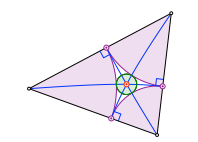
1.4 Schließungsfigur

Wir zeichnen Kreisbögen ins Dreieck. Die Figur schließt sich nach sechs Schritten.

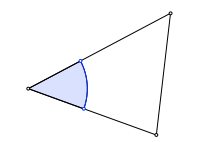
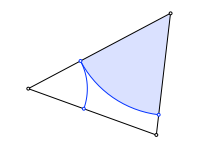
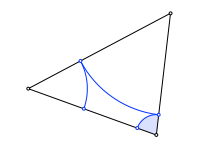
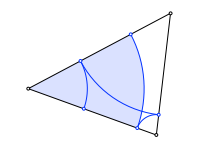
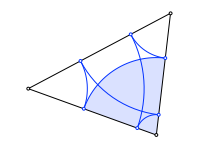
Schließungsfigur

Die sechs Punkte auf den Dreiecksseiten liegen auf einem Kreis. Dieser ist konzentrisch zum Inkreis.

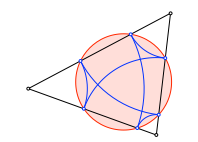
Sechspunktekreis

1.5 Besserer Startpunkt

Wir verschieben den Startpunkt etwas.

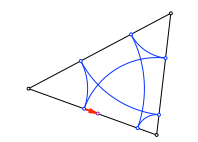
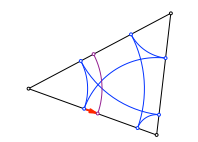
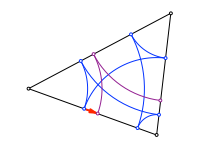
Die Königskinder kommen sich näher

Nach drei Schritten haben wir dieselbe Verschiebung in der entgegengesetzten Richtung. Die beiden Punkte nähern sich an.

Beim Startpunkt in der Mitte schließt sich die Figur schon nach drei Schritten. Es ergeben sich die Berührpunkte des Inkreises.

Diese Denkweise wurde von Adam Ries (1492/93-1559) als regula falsi (Regel des falschen Ansatzes) kultiviert.

Optimaler Startpunkt. Inkreis

1.6 Inkreis mit Hyperbeln

Wir zeichnen eine Hyperbel mit zwei Dreiecksecken als Brennpunkte, welche durch die dritte Ecke verläuft. Dies geht auf drei Arten. Die drei Hyperbeln schneiden sich in einem Punkt und durchsetzen die Dreiecksseiten rechtwinklig. Die Schnittpunkte mit den Dreiecksseiten sind die Berührpunkte des Inkreises. Beweise als Übungsaufgabe.

Hyperbeln

Der Schnittpunkt der drei Hyperbeln ist allerdings nicht das Zentrum des Inkreises, aber das Zentrum des Kreises, der die drei Kreisbögen der früheren Konstruktion berührt.

Inkreis und Innenkreis

1.7 Zwischenspiel: Problem des Apollonios

Apollonios von Perge (ca. 262 v. Chr. – ca. 190 v. Chr.): Zu drei Kreisen ist ein vierter Kreis gesucht, der die drei gegebenen Kreise berührt.

Dazu zeichnen wir erst die Mittelpunkte der drei Minimalabstände. Ein geeigneter Kreis um einen solchen Mittelpunkt berührt zwei der drei gegebenen Kreise. Wir der Kreisradius etwas vergrößert, wandert der Mittelpunkt auf der Hyperbel mit den Brennpunkten in den Zentren der beiden berührten Kreise.

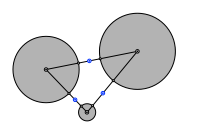
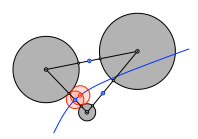
Minimalabstände. Hyperbel

Die drei nach dieser Überlegung konstruierten Hyperbeln schneiden sich in einem Punkt. Dieser ist der Mittelpunkt des gesuchten Kreises.

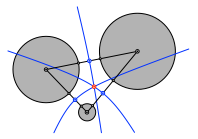
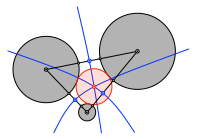
Problem des Apollonius

Diese Konstruktion geht auf Adriaan van Roomen (1561-1615) zurück.

Puritaner werden bei dieser Konstruktion die Nase rümpfen. Sie ist nicht mit Zirkel und Lineal durchführbar. Allerdings ist da zu bemerken, dass Konstruktionen mit „Zirkel und Lineal“ auch nur in unserer Vorstellung exakt sind. Die Konstruktion von van Roomen ist aber rein logisch völlig exakt. Mit heutigen technischen Möglichkeiten (DGS) ist auch ein hinreichend gute Zeichnung möglich.

Zu drei gegebenen Kreisen gibt es bis zu 2³ = 8 Kreise, welche die drei gegebenen Kreise berühren.

2 Vierecke

2.1 Wenn’s nicht geht, geht’s nicht

Wenn wir bei einem beliebigen Viereck Bögen einzeichnen und den Startpunkt verschieben, verschiebt sich der Endpunkt um gleich viel in der gleichen Richtung. Die Königskinder kommen also nicht zusammen.

Die Königskinder kommen sich nicht näher

2.2 Tangentenviereck

Wenn wir umgekehrt in einem Tangentenviereck Bögen einzeichnen, schließt sich die Bogenfigur bei beliebigen Startwerten nach vier Schritten.

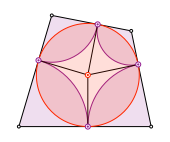
Tangentenviereck

Da die von einer Ecke ausgehenden Tangentenabschnitte jeweils gleich lang sind, erhalten wir für ein Tangentenviereck die notwendige Bedingung, dass die Summe der Gegenseiten konstant ist.

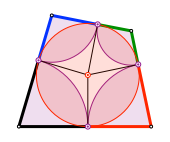
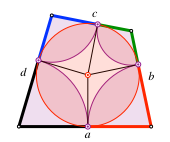
Summe der Gegenseiten konstant

Es gilt:

a + c = b + d (1)

Äquivalent dazu verschwindet die alternierende Seitensumme:

a – b + c – d = 0 (2)

Schließlich gibt es auch eine Differenzengleichheit:

a – b = d – c (3)

Man kann zeigen, dass diese notwendigen Bedingungen für ein Tangentenviereck auch hinreichend sind. Die Bedingungen legen allerdings das Tangentenviereck noch nicht fest.

2.3 Zwei Sätze über Tangentenvierecke

2.3.1 Newton

Wir verbinden gegenüberliegende Berührungspunkte des Inkreises. Der Schnittpunkt der beiden Verbindungslinien liegt auf dem Diagonalenschnittpunkt. Beweis siehe (F. G.-M. (Frère Gabriel-Marie) 1920, p. 573).

Satz von Newton

2.3.2 Kissing circles

Wir zerlegen das Tangentenviereck mit einer Diagonalen in zwei Dreiecke. Die beiden Inkreise der Teildreiecke berühren sich.

Kissing circles

Dies ist genau bei Tangentenvierecken der Fall. Warum?

2.4 Gelenkmodelle

Ein Gelenkmodell, das einer dieser Bedingungen genügt, kann verformt werden. In jeder Situation ergibt sich ein Tangentenviereck.

Den größten Inkreis und damit auch den größten Flächeninhalt erhalten wir für dasjenige Viereck, das auch einen Umkreis hat (Sehnentangentenviereck). Es handelt sich hier um eine Variante des isoperimetrischen Problems.

Die folgende Abbildung zeigt ein echtes Gelenkmodell in zwei verschiedenen Positionen. Die Tangentenviereckbedingung kann durch Abzählen der Lochabstände verifiziert werden.

Gelenkmodell

Die optimale Position finden wir, indem wir das Modell über einen Kegel stülpen.

Optimale Lösung

Die Bedingung (2) (Verschwinden der alternierenden Seitensumme) gestattet, das Gelenkmodell wie ein Taschenmesser zusammenzuklappen.

Klappviereck

2.5 Konstruktion mit einer Hyperbel

Die Bedingung (3) führt zu einer Konstruktion mit einer Hyperbel. Die beiden Brennpunkte und zwei Hyperbelpunkte bilden ein Tangentenviereck.

Konstruktion mit einer Hyperbel

3 Im Raum: Tangententetraeder

Die folgende Abbildung zeigt ein Tetraeder mit einer Kugel, welche alle sechs Kanten des Tetraeders berührt.

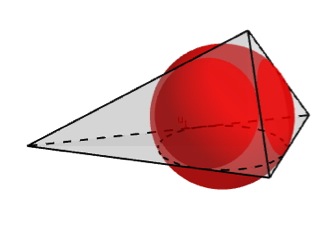
Tangententetraeder

Einzeichnen der Berührungspunkte und Weglassen der Kantenberührkugel führt zur Einsicht dass die Summen der Gegenkanten konstant sind.

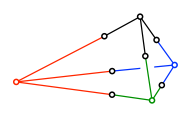
Summen der Gegenkanten konstant

4 Fünfeck

4.1 Bogen

In einem beliebigen Fünfeck zeichnen wir die Eckenbogen ein.

Im Fünfeck

Wir haben im Prinzip dieselbe Situation wie beim Dreieck. Trotzdem hat das Fünfeck nicht automatisch einen Inkreis. Es ist sozusagen erst die notwendige Bedingung dafür automatisch erfüllt.

Die folgende Abbildung zeigt die Bögen für ein Gelenkfünfeck. Es sind zusätzlich die erwarteten Berührungspunkte mit einer Mustertütenklammer markiert. Diese Klammern sind also keine Gelenke.

Gelenkmodell

4.2 Tangentenfünfeck

Erst wenn wir das Gelenkmodell über den Kegel strammstülpen, ergibt sich das Tangentenfünfeck.

Tangentenfünfeck

4.3 Tangentenpentagramm

Mit denselben Bauteilen des Gelenkmodells in derselben Reihenfolge und denselben Berührungspunkten, aber mit doppeltem Umlauf, ergibt sich ein Tangentenpentagramm.

Weihnachten kommt bestimmt

5 Berechnungen

Wir führen die Berechnungen exemplarisch am Fünfeck durch.

In einem ersten Schritt berechnen wir die Tangentenabschnitte, also die Radien der violetten Bögen.

Im zweiten Schritt berechnen wir den Inkreisradius des Tangentenfünfeckes.

5.1 Tangentenabschnitte

Wir verwenden die Bezeichnungen der folgenden Figur.

Bezeichnungen

Es ist:

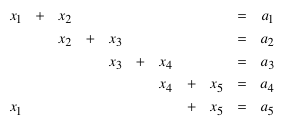(7)

Durch alternierendes Addieren der Zeilen von (7) ergibt sich:

(8)

Mit zyklischer Vertauschung erhalten wir:

(9)

Das Gleichungssystem (7) hat die Koeffizientenmatrix:

(10)

Für die Determinanten der quadratischen Matrix links erhalten wir exemplarisch:

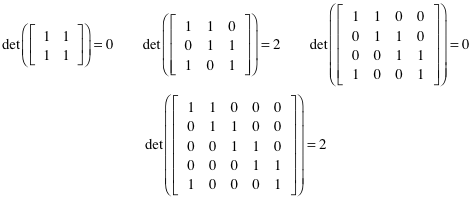(11)

Es ergibt sich eine Fallunterscheidung gemäß der Parität von n:

Für ungerades n erhalten wir die Determinante 2. Dies kann zum Beispiel mit der Entwicklung nach der ersten Spalte gezeigt werden. Das Gleichungssystem ist regulär und hat genau eine Lösung.

Für gerades n erhalten wir die Determinante 0. Die alternierende Zeilensumme verschwindet. Wir sind im singulären Fall. Wenn die alternierende Summe der Koeffizienten nicht verschwindet, haben wir keine Lösung. Sonst unendlich viele Lösungen.

5.2 Inkreisradius

Für die Berechnung des Inkreisradius r arbeiten wir gemäß der folgenden Abbildung.

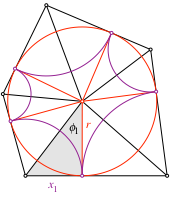
Berechnung des Inkreisradius r

Es ist zunächst:

(11)

Analog für die übrigen Sektoren. Da jeder Winkel zweimal vorkommt, ist:

(12)

Somit erhalten wir für den Inkreisradius r die Bestimmungsgleichung:

(13)

Im Beispiel unseres Gelenkmodells heißt das:

(14)

Mit CAS erhalten wir die Lösung:

(15)

Das Pentagramm-Gelenkmodell hat die doppelte Umlaufszahl. Anstelle der Gleichung (14) erhalten wir daher:

(16)

Diese Gleichung hat die Lösung:

(17)

Literatur

F. G.-M. (Frère Gabriel-Marie) (1920): Exercices de géométrie. Comprenant l’exposé de méthodes géométriques et 2000 questions résolues. Sixième édition. Tours: Maison A. Mame et fils / Paris: J. de Gigord.
Réimpression: 1991, Edition Jacques Gabay, Sceaux. ISBN 2-87647-083-7