Hans Walser

Halbreguläre Figuren

Graz, Tag der Mathematik, Do, 8. Februar 2024

Zusammenfassung: Bei einem regulären Fünfeck klappen wir eine Ecke ein und erhalten als Restfigur ein zwar noch gleichseitiges, aber nicht mehr gleichwinkliges Fünfeck. Damit können wir Parkette auslegen sowie Bandornamente und Spiralen, ebenso Flächenfüllungen mit Drehsymmetrie.

Mit zwölf halbregulären Fünfecken lässt sich ein halbreguläres Dodekaeder bauen. Es ist die Ergänzung zu einem regulären Dodekaeder und hat dieselbe Topologie. Das halbreguläre Dodekaeder ist ein Stern mit acht Spitzen, aber verschieden vom Kepler-Stern. Zusammen mit dem regulären Dodekaeder lässt sich der Raum lückenlos und überlappungsfrei ausfüllen.

1 Halbreguläres Fünfeck

Das reguläre Fünfeck kann nicht für eine Parkettierung der Ebene verwendet werden. Es bleibt eine Lücke von 36° (Abb. 1).

Abb. 1: Keine Parkettierung mit regelmäßigen Fünfecken

Wir modifizieren das reguläre Fünfeck: Wir klappen eine Ecke ein (Abb. 2). Die Restfigur ist ein halbreguläres Fünfeck. Es hat zwar gleich lange Seiten, aber ungleiche Winkel.

Abb. 2: Halbreguläres Fünfeck

2 Kombination mit dem regulären Fünfeck

Zusammen mit dem regulären Fünfeck kann das halbreguläre Fünfeck für eine Parkettierung der Ebene verwendet werden (Abb. 3a).

Abb. 3: Parkett mit regulären und halbregulären Fünfecken

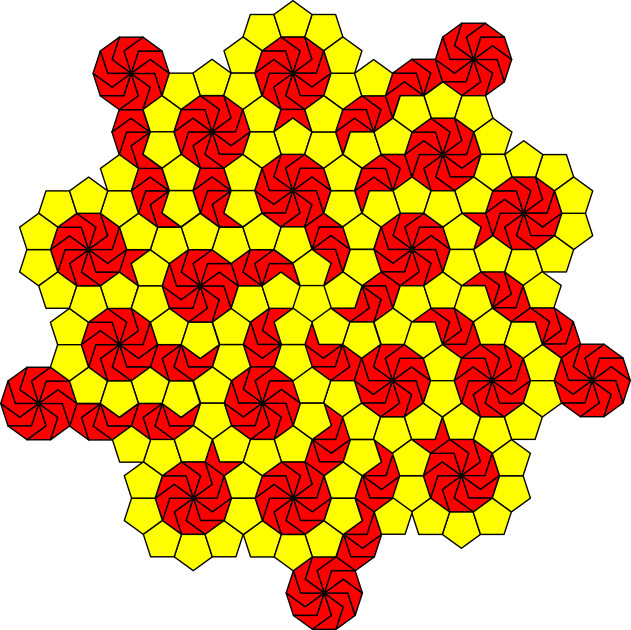
Das Parkett enthält Translationssymmetrie (blaue Pfeile in Abb. 3b), Achsensymmetrie (rot) und Schubspiegelsymmetrie (violett).

Die Abbildung 4 zeigt eine Unterteilung der Ebene mit fünfteiliger Drehsymmetrie.

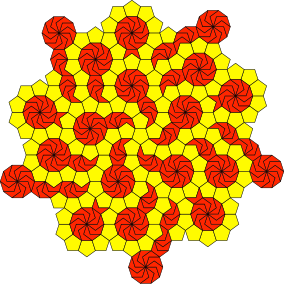
Abb. 4: Fünfteilige Drehsymmetrie

3 Bandornamente und Flächenornamente

Wir können aber auch mit dem halbregulären Fünfeck allein arbeiten.

Die Abbildung 5 zeigt ein Bandornament. Es hat nur Translationssymmetrie. Wenn wir die Farben ignorieren, erhalten wir zusätzlich Schubspiegelsymmetrie.

Abb. 5: Bandornament

Die Abbildung 6a zeigt eine Stapelung des Bandornamentes der Abbildung 5.

Hier werden wir leicht das Opfer einer optischen Täuschung. Sind die horizontalen Linien parallel?

Die Abbildung 6b zeigt ein eleganteres Beispiel ohne Bandornamente.

Worin besteht der Unterschied zwischen den Parketten der Abbildungen 6c und 6d?

Abb. 6: Parkette

4 Ringe und Spiralen

Die Abbildung 7a zeigt eine Konstellation mit konzentrischen Ringen. In der Abbildung 7b sind die Farben so ausgetauscht worden, dass immer verschiedene Farben an einer Kante erscheinen.

Abb. 7: Konzentrische Ringe

In der Abbildung 8a sehen wir zunächst keine Struktur. Tatsächlich enthält die Figur aber eine Spirale konstanter Breite, also eine archimedische Spirale (Abb. 8b).

Abb. 8: Spirale

In der Abbildung 9 haben wir zwei beziehungsweise zehn Spiralen.

Abb. 9: Weitere Spiralen

5 Im Raum

Aus zwölf regulären Fünfecken können wir das reguläre Dodekaeder bauen (Abb. 10a). Zusammen mit dem regulären Tetraeder, dem Würfel, dem regulären Oktaeder und dem regulären Ikosaeder gehört es zu den fünf platonischen Körpern.

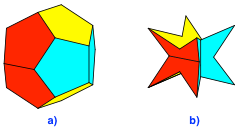
Abb. 10: Reguläres und halbreguläres Dodekaeder

Mit zwölf halbregulären Fünfecken können wir entsprechend das halbreguläre Dodekaeder bauen (Abb. 10b). Das halbreguläre Dodekaeder wurde von Carl Kemper (1881-1957) beschrieben. Es wird daher auch als Kemper-Stern bezeichnet.

6 Zusammenhang mit dem Würfel

Das halbreguläre Dodekaeder passt offensichtlich in einen Würfel (Abb. 11b). Wir können aber auch auf den Seiten des regulären Dodekaeders einen Würfel einzeichnen (Abb. 11a).

Abb. 11: Zusammenhang mit dem Würfel

Wir können daher das reguläre Dodekaeder als Würfels mit sechs aufgesetzten Walmdächern sehen. Überraschenderweise ist das halbreguläre Dodekaeder genau die Restfigur nach dem Abschneiden von sechs Walmdächern vom Würfel. Wir können daher das reguläre Dodekaeder als „positiv“ und das halbreguläre Dodekaeder als „negativ“ sehen. Der Walmdachüberschuss des regulären Dodekaeders entspricht dem Walmdachdefizit des halbregulären Dodekaeders.

Die Abbildung 12 zeigt den Zusammenhang zwischen den beiden Dodekaedern.

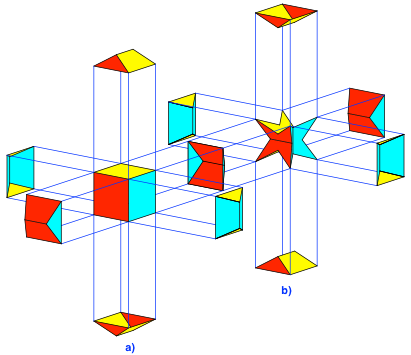
Abb. 12: Walmdächer

Das Walmdach in der Bildmitte wandert vom Würfel rechts (Abb. 12b) zum Würfel links (Abb. 12a). Das erinnert an die Situation von Anionen und Kationen in der Chemie.

Das einzelne Walmdach hat die Ausmaße gemäß Abbildung 13.

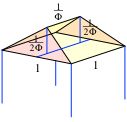
Abb. 13: Ausmaße eines Walmdaches

Dabei bezeichnet den Goldenen Schnitt (Walser 2013) . Die Firsthöhe des Walmdaches ist .

7 Sterne mit acht Spitzen

Das halbreguläre Dodekaeder ist ein Stern mit acht Spitzen (Abb. 14b). Es unterscheidet sich aber vom ebenfalls achtspitzigen Kepler-Stern (stella octangula, Abb. 14a).

Abb. 14: Kepler-Stern und halbreguläres Dodekaeder

8 Symmetriegruppen

Das reguläre und das halbreguläre Dodekaeder haben unterschiedliche Symmetriegruppen. Das reguläre Dodekaeder hat (trivialerweise) die Symmetriegruppe des Dodekaeders, das halbreguläre Dodekaeder hat nur die Symmetriegruppe des regulären Tetraeders.

9 Topologie

Das reguläre und das halbreguläre Dodekaeder haben dieselbe Topologie (Abb. 15 und 16).

Beide haben 20 Ecken, aber im halbregulären Dodekaeder sind 12 der 20 Ecken hyperbolisch.

Abb. 15: Ecken, Kanten und Seitenflächen

Beide haben 30 Kanten, aber im halbregulären Dodekaeder sind 6 der 30 Kanten wie eine Talsohle.

Das reguläre Dodekaeder hat 12 reguläre Fünfecke als Seitenfläche, das halbreguläre Dodekaeder aber 12 halbreguläre Fünfecke.

Die Abbildung 16 zeigt den topologischen Zusammenhang zwischen Ecken und Kanten. Hierin unterscheiden sich das reguläre und das halbreguläre Dodekaeder nicht.

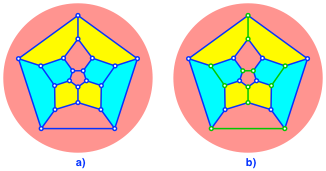
Abb. 16: Diagramme

10 Modell

Die Abbildung 17 zeigt ein Papiermodell des halbregulären Dodekaeders.

Abb. 17: Papiermodell

Für das Modell werden 6 Bauteile gemäß Abbildung 18 benötigt. Die schwarzen Linien sind Schnittlinien, die rote Linie ist ein Talfalt und die blauen Linien sind Bergfalte.

Abb. 18: Schnittmuster

Die roten Teile sind im Modell außen sichtbar. Die grauen Teile werden seitlich eingesteckt.

Tipp: Das Modell ist nicht besonders stabil. Ich habe daher zunächst ein Unterbaumodell in reduzierter Größe (98%) gebaut und darüber als zweite Lage das eigentlich Modell.

11 Eierbecher

Wegen der relativen Situation zwischen den beiden Dodekaedern (Abb. 12) kann das reguläre Dodekaeder dem halbregulären Dodekaeder aufgesetzt werden wie ein Ei auf den Eierbecher (Abb. 19).

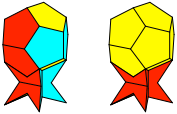
Abb. 19: Ei und Eierbecher

12 Raumfüllung

Weder das reguläre noch das halbreguläre Dodekaeder sind „Raumfüller“ (Coxeter 1973, S. 68f), mit denen der Raum lückenlos und überlappungsfrei aufgefüllt werden könnte. Hingegen können wir den Raum mit einer Kombination von regulären und halbregulären Dodekaedern gemäß Abbildung 19 auffüllen (Abb. 20).

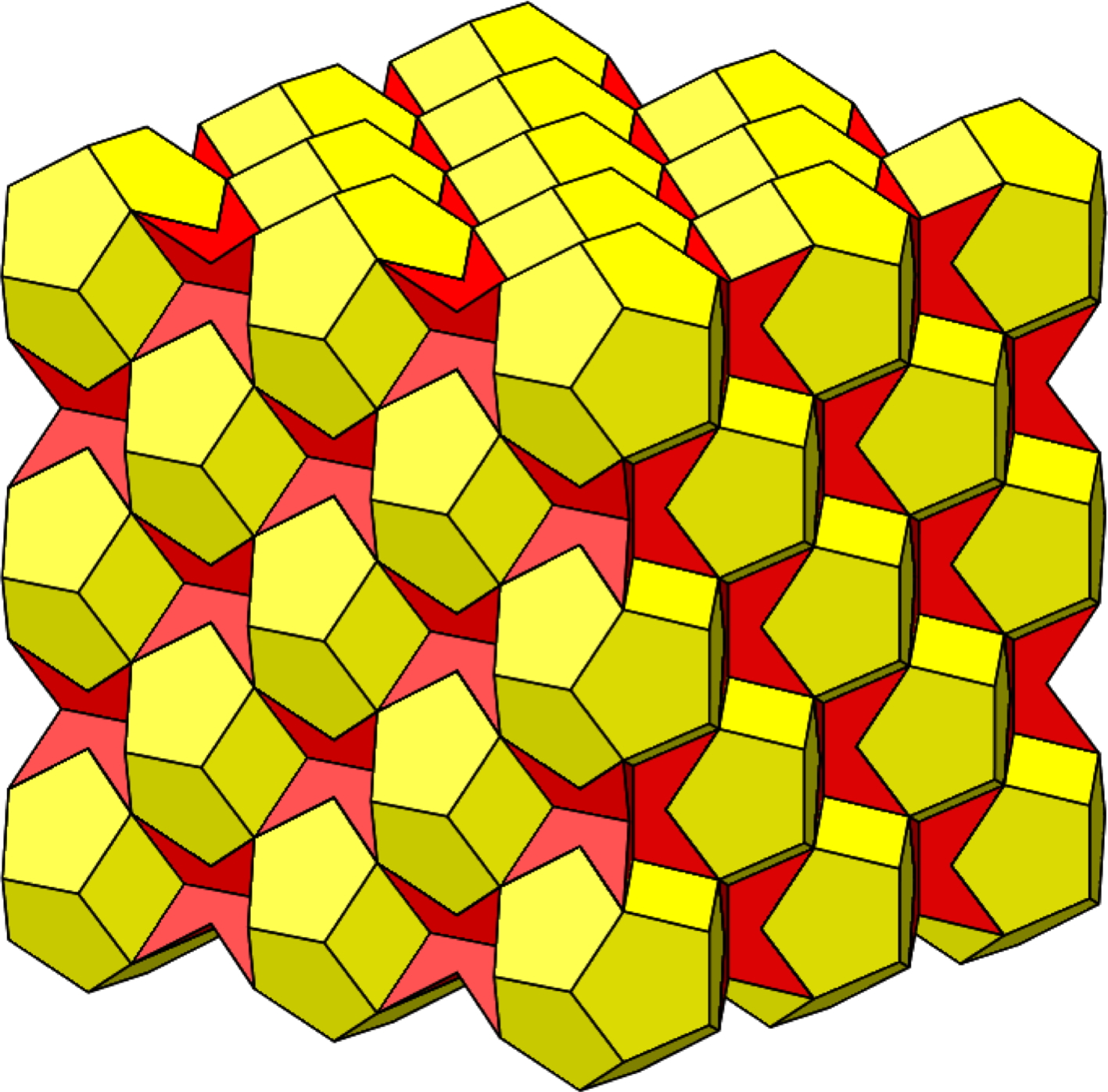
Abb. 20: Raumfüller

Die Figur der Abbildung 20 ist das räumliche Analogon zur Figur der Abbildung 3.

Der Beweis für die Raumfüllungseigenschaft ist einfach: Der Würfel ist ein Raumfüller. Wir denken uns nun in einer Würfel-Raumfüllung die einzelnen Würfel schwarz und weiß gefärbt wie ein dreidimensionales Schachbrett. Darin können wir von den schwarzen Würfeln je sechs Walmdächer abspalten und an die benachbarten weißen Würfel anheften.

13 Dodekaeder-Transformationen

Die Abbildung 21 zeigt eine Folge von Dodekaedern.

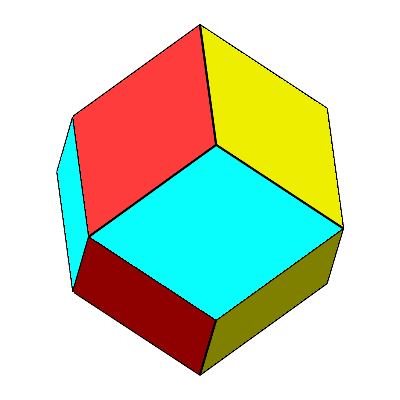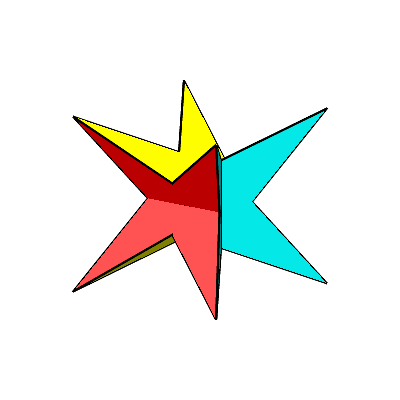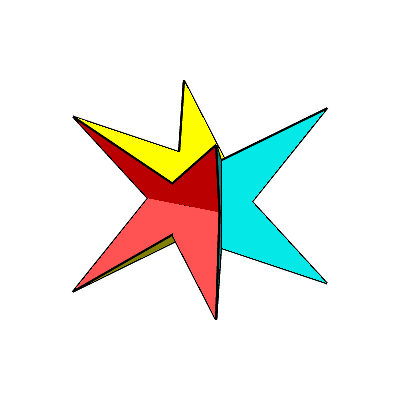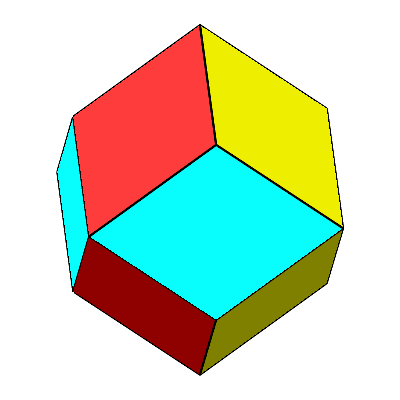
Abb. 21: Dodekaeder-Transformationen

Die Idee dabei ist, dass wir an die zwölf Kanten eines Würfels Ebenen mit gleichem Neigungswinkel gegenüber den Würfelseiten anlegen. Wir beginnen mit einem Winkel von 45° (Abb. 22).

Abb. 22: Winkel von 45°

Dies führt zum Rhombendodekaeder (Abb. 23 und 24).

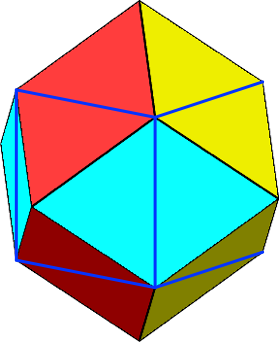
Abb. 23: Rhombendodekaeder mit Würfel

Abb. 24: Rhombendodekaeder ohne Würfel

Nun verkleinern wir den Neigungswinkel auf arctan(1/Φ) ≈ 31.717°. Damit erhalten wir das regelmäßige Dodekaeder (regelmäßiges Pentagondodekaeder) (Abb. 25). Das regelmäßige Dodekaeder ist einer der fünf platonischen Körper.

Abb. 25: Regelmäßiges Dodekaeder

Wird der Neigungswinkel auf 0° verkleinert, entsteht ein Würfel (Abb. 26).

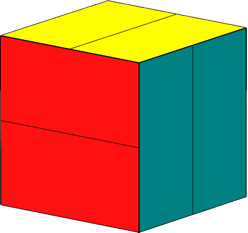
Abb. 26: Würfel mit geschlossenen Fensterläden

Nun verkleinern wir den Neigungswinkel weiter auf –arctan(1/ Φ) ≈ –31.717°. Es entsteht das halbreguläre Dodekaeder (Kemper-Stern) (Abb. 27).

Abb. 27: Halbreguläres Dodekaeder

Bei einem Neigungswinkel von –45° bleiben nur die Raumdiagonalen des Würfels übrig (Abb. 28).

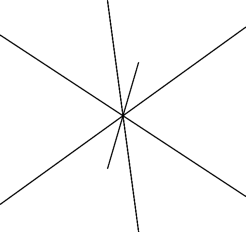
Abb. 28: Raumdiagonalen des Würfels

Bei einem Neigungswinkel von –arctan(Φ) ≈ –58.283° ergibt sich der sogenannte Ikosaederstern (manchmal auch als großes Dodekaeder bezeichnet) (Abb. 29). Dies ist einer der vier Poinsot-Körper. Er hat Selbstdurchdringungen. Die zwölf Seitenflächen sind regelmäßige Pentagramme.

Abb. 29: Ikosaederstern

Literatur

Coxeter, H.S.M. (1973): Regular Polytopes. Third Edition. New York: Dover 1973. ISBN 0-486-61480-8.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.

Websites

[1] Stella octangula (abgerufen 14.12.2023)

http://mathworld.wolfram.com/StellaOctangula.html