Hans Walser

Umwörter

50. Jahrestagung der Gesellschaft für Didaktik der Mathematik

07.03. bis 11.03.2016

Heidelberg

Zusammenfassung

Das treibt uns alle um. Umwörter sind Ausdrücke oder Formulierungen, die auf sich selber zurückkommen. Es werden einige Beispiele aus dem Unterrichtsalltag diskutiert. Zur Sprache kommen insbesondere Verspätungen, Max und Moritz, sprachlich bedingte Trugschlüsse, Lern-Umgebungen, schiefer Pythagoras, Parkett.

1 Umwörter

In Ulm und um Ulm und um Ulm herum

Zunächst können einfach Wörter mit der Vorsilbe um- als Umwörter bezeichnet werden. Dann aber auch Wörter und Ausdrücke mit einer zyklischen Bedeutung, aber auch Zirkelschlüsse oder Tautologien.

2 Beispiele

2.1 Verspätung

Der EC 8 nach Zürich erhält 21 Minuten Verspätung. Grund dafür sind Verzögerungen im Betriebsablauf.

Zunächst: Pünktlichkeit ist eine Kardinaltugend. Verspätungen werden auf die Minute genau angegeben. Nachdem die Kardinaltugend der Pünktlichkeit auf der Basisebene des Bahnbetriebes nicht mehr funktioniert, wird sie auf die Metaebene der Beschreibung der Unpünktlichkeit verlagert. Pünktlich sind wir allemal.

Die angebliche Begründung mit den Verzögerungen im Betriebsablauf ist nur eine Umschreibung des Basisbegriffs Verspätung. Durch die breitere Formulierung soll wohl der Eindruck einer inhaltlichen Begründung entstehen.

2.2 Winkel

Winkelbegriff: »two lines meeting at a point with an angular relation between them« (Mitchelmore und White, 1998, S. 5).

Für einen außenstehenden Leser kann diese Formulierung als Tautologie erscheinen.

2.3 Testfrage

Wie lautet der Fachausdruck für Fachausdruck? — Als korrekte Antworten sind Fachausdruck und Terminus technicus zugelassen.

2.4 Hilfe zur Selbsthilfe

Hilfe zur Selbsthilfe. Weiter keine Hilfe. Also keine Hilfe. Hilfe zur Selbsthilfe.

2.5 Lernen lernen

Lernen lernen: Wer lernen kann, braucht’s nicht mehr zu lernen. Wer’s nicht kann, kann’s auch nicht lernen.

2.6 Der Klassiker

Wovon man nicht sprechen kann, darüber muss man schweigen (Wittgenstein 1922, Schlusssatz).

2.7 Zitat

Der Buchstabe tötet, der Geist macht lebendig. 2. Kor 3,6.

Die Koordinaten am Ende des Satzes machen das Zitat zu einer Buchstabenagglo.

3 Umfang

An einem Wochenende im Mathematikum in Gießen [1] studierte ich die Relation zwischen den Besuchern und den Exponaten („Museumsblick“).

Ein Exponat besteht aus einem Rad mit einem Stift am Rand. Dieser fährt beim Abrollen des Rades über die Kontur einer Zykloide (Abb. 1). Ein etwas angejahrter Mann fuhr mit dem Finger die Kontur der Zykloide entlang und erklärte seiner Begleiterin, das sei der Weg eines Kreispunktes bei einer Umdrehung, also der Umfang des Kreises. — Es ist schwer, dieser Argumentation zu begegnen. Als ich dann endlich meine Gedanken geordnet hatte, waren die beiden verschwunden. Man soll nie über den eigenen Unterricht reflektieren, sonst verliert man den Anschluss an seine Schüler.

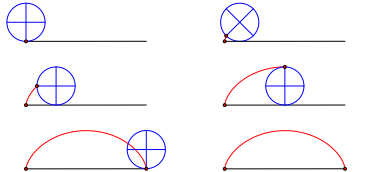
Abb. 1: Abrollen eines Rades, Zykloidenbogen

Abb. 2: Christopher Wren (1632-1723)

Nun ist es so, dass die Länge eines Zykloidenbogens bereits von Christopher Wren (1632-1723) berechnet wurde: Beim Abrollen eines Rades mit dem Radius r ergibt sich für den Zykloidenbogen die Länge 8r. Dies ist ein bemerkenswertes ganzzahliges Resultat, das die irrationale Kreiszahl nicht enthält (Abb. 3).

Abb. 3: Längenverhältnisse

Die „richtige“ Umfanglänge erscheint am Boden als abgerollte Strecke.

Den Umfang erhalten wir als Weglänge eines Kreispunktes bei einer Umdrehung, wenn das drehende Rad nicht rollt. Das ist die Situation, in der man Schneeketten montieren muss, um weiterzukommen.

4 Weg und Umweg

Weg und Umweg werden als Gegensatzpaar verstanden, das eine definiert sich durch das andere.

4.1 Umweg

Die Abbildung 3 ist eine Illustration des Satzes, dass der Umweg länger ist als der direkte Weg. Als Argument für diesen Satz wird oft vorgebracht, dass der direkte Weg eben der kürzeste Weg ist und daher kürzer als jeder Umweg.

Es dürfte schwerfallen, Schülerinnen und Schüler zu einem Beweis etwa der Dreiecksungleichung zu motivieren.

4.2 Der direkte Weg

Abb. 4: Vorgeschriebene Fahrtrichtung: geradeaus

Immer der Nase nach.

... so geh hübsch sittsam und lauf nicht vom Wege ab! (Grimm 1812)

La línia recta és creació de l'home; la línia corba, de Déu. (Antoni Gaudí)

Keine Seitenkrümmung, geodätische Linie:

(1)

5 Schere – Stein – Papier

Die englische Sprechweise ist Rock – Paper – Scissors. Die Reihenfolge ist anders, die zyklische Reihenfolge aber gleich.

Abb. 5: Kreisverkehr

5.1 Bemerkung zum Drehsinn

Der positive Drehsinn wird in der Regel als Gegenuhrzeigersinn serviert. Wegen der Umkehrung Gegen- ist das eine schlechte Merkregel. Besser ist (in Ländern mit Rechtsverkehr) eine Anlehnung an den Kreisverkehr.

5.2 Nostalgisches Beispiel

Max und Moritz: Lämpel ist dumm

Lehrer Lämpel: Pestalozzi ein Versager

Pestalozzi: Max und Moritz müssen an Kopf, Herz und Hand gefördert werden

5.3 Aktuelles Beispiel

Die folgenden gelegentlich gehörten Aussagen sind wohl nur zur Hälfte wahr.

(1) Schüler: Lehrer sind dumm

(2) Lehrer: Didaktiker gescheiterte Lehrer

(3) Didaktiker: Ohne Zweifel besteht Konsens in der Community, dass Schülerinnen und Schüler nachhaltig gefördert werden müssen.

Relativierungen:

(1) Die Aussage kann personalisiert so formuliert werden:

(2)

Kommentar des Mathematiklehrers: Diese authentische Schülerformulierung zeigt, dass der Schüler den Limes-Begriff nicht verstanden hat. Er hätte ebenso gut Großhirn statt Kleinhirn schreiben können. Null ist null.

Kommentar des Deutschlehrers: Der Schüler wollte formulieren, dass der Sachverhalt eine kleine Null sei. Das ist noch weniger als eine große Null. Wobei eine große Null vielleicht noch schlimmer ist als eine kleine Null.

Nullen gibt es nicht nur in verschiedenen Farben, sondern auch in verschiedenen Größen.

Wer parallel sowohl in der Ausbildung von Lehrpersonen wie auch von Ingenieuren oder Naturwissenschaftlern tätig war, hat vielleicht die Erfahrung gemacht, dass deren Rezeptionsfähigkeit unterschiedlich ist. Eine ironische Zwischenbemerkung, die bei Ingenieuren oder Naturwissenschaftlern zu hellem Gelächter im Hörsaal führt, löst bei Lehramtskandidaten fragendes Erstaunen aus und bedarf einer zusätzlichen Erklärung. Spitz formuliert: Didaktik ist offenbar das, was man den Lehrern noch extra sagen muss. Gerne wird nun das Kompensationsprinzip bemüht: Lehrpersonen haben dafür höhere soziale Kompetenzen (Strittmatter: Ein bisschen dumm, dafür ein gutes Herz). Nach meiner Erfahrung sind allerdings soziale und intellektuelle Fähigkeiten stochastisch unabhängig verteilt. Das Kompensationsprinzip gilt nicht.

(2) Jeder Schulleiter kennt Lehrpersonen, die von einer Schule an die nächste weiterempfohlen werden („Wanderpokale“) und schließlich in den Hafen einer pädagogischen Hochschule einfahren. Eine Analyse der Biografie dieser Leute ergibt folgendes: Sie sind irgendwo auf ihrem Bildungsgang – sei es als Schüler, Student, Lehrer oder Schulleiter – nicht ganz glücklich geworden und suchen die „Schuld“ nicht bei sich selber, sondern am System Schule, das zu verändern sie sich nun berufen fühlen.

(3) Ich bin als Lehrer immer davon ausgegangen (Normalverteilung) dass die Hälfte meiner Schülerinnen und Schüler klüger ist als ich. Diesen Schülerinnen und Schülern gegenüber muss sich die Schule auf ihre Kernaufgabe beschränken: Vermittlung von tradierten Fakten und Methoden. — Begabtenförderung hat ja immer etwas von Proselytenmacherei. Begabte Kinder fördern sich selber und sollen daran nicht gehindert werden.

6 Lern-Umgebung

Abb. 6: Gottfried Wilhelm Leibniz (1646-1716)

Gottfried Wilhelm Leibniz (1646-1716) soll gesagt haben, er habe jeweils beim Erwachen so viele Ideen, dass der Tag meistens nicht ausreiche, um alle Ideen umzusetzen. Stellen wir uns nun vor, Leibniz wäre gleich beim Erwachen in eine Lernumgebung eingebüxt worden.

Die beste Lern-Umgebung ist die Umgebung.

7 Ausbrechen aus der Lernumgebung

Ein Ausbruch hat auch einen ethischen oder, von der Umwelt gesehen, kriminellen Aspekt.

Wir alle kennen die Pythagoras-Ikone (Abb. 7). Sakrosankt ist dabei der rechte Winkel.

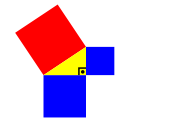
Abb. 7: rot = blau

Max und Moritz, diese beiden, fügen zunächst ein zweites Hypotenusen-Quadrat hinzu, damit jeder eins hat (Abb. 8).

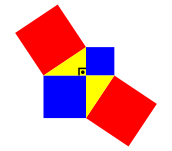
Abb. 8: rot = 2 × blau

Und nun wackeln sie am rechten Winkel (Abb. 9). Die eine Hypotenuse wird kürzer, die andere länger. Gilt das Kompensationsprinzip, und wenn ja, in welchem Sinne?

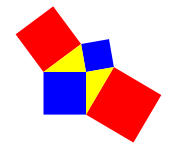
Abb. 9: Pythagoras wackelt

Tatsächlich gilt immer noch, dass die beiden roten Quadrate zusammen doppelte Fläche haben wie die beiden blauen. Der Beweis geht sehr einfach mit dem Kosinussatz. Wir verwenden dazu die Bezeichnungen der Abbildung 10.

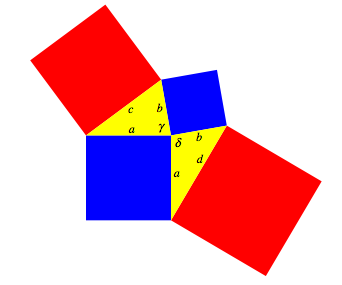
Abb. 10: Bezeichnungen

Wegen ist:

(3)

Aus dem Kosinussatz erhalten wir einerseits

(4)

und andererseits:

(5)

Addition von (4) und (5) ergibt die Behauptung. Es ist rot = 2 × blau.

Ebenso kann gezeigt werden, dass die beiden gelben Dreiecke denselben Flächeninhalt haben. Es ist:

(6)

8 Max und Moritz-Theorem

Gerügt über den unschönen Faktor 2 in rot = 2 × blau halbieren Max und Moritz die blauen Quadrate und vierteln die roten (Abb. 11).

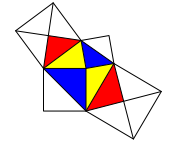
Abb. 11: Halbieren und vierteln

Nun ist rot = blau, das Max und Moritz-Theorem (Abb. 12).

Abb. 12: rot = blau

Die Figur lässt sich in ein Parkett einpassen (Abb. 13). Die gelben und grünen Dreiecke haben alle den gleichen Flächeninhalt.

Abb. 13: Parkett

Literatur

Busch, Wilhelm (1865): Max und Moritz. Eine Bubengeschichte in sieben Streichen. München: Verlag von Braun und Schneider.

Grimm, Jakob und Wilhelm (1812): Kinder- und Hausmärchen, Band I.

Mitchelmore, M. und White, P. (1998): Development of Angle Concepts: A Framework for Research. In: Mathematics Education Research Journal 10.3, S. 4–27.

Wittgenstein, Ludwig (1922): Tractatus logico-philosophicus. London: Kegan Paul, Trench, Trubner.

Websites

[1] Mathematikum Gießen (abgerufen 29. 10. 2015)

http://www.mathematikum.de

Version 30. Januar 2016