Hans Walser

Universität Basel

Gleichgewicht

Thales, Pythagoras und Archimedes

SLA-Tagung, St. Gallen

Samstag, 17. November 2012

Zusammenfassung

Der Kreis des Thales und Satz des Pythagoras lassen sich auf nahe liegende Weise verallgemeinern. Die zugehörigen Figuren haben eine Gleichgewichtseigenschaft, sie sind in sich ruhend. Damit kommen als Querbezug zur Physik die Hebelgesetze des Archimedes ins Spiel. Eine zentrale Rolle spielt die Summe von Quadraten von Abständen, die wir auch in der Stochastik (Durchschnitt, Varianz) antreffen. Bei der Organisation der Hebelmechanismen treten Fragen der Topologie und der Kombinatorik auf.

1 Rollt der Kreis ab?

Auf der Kreislinie sind fünf gleiche Punktmassen in unregelmäßigen Abständen verteilt (Abb. 1). Rollt der Kreis ab?

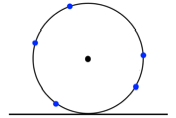
Abb. 1: Rollt der Kreis ab?

Die Frage ist, ob der Schwerpunkt der fünf Massen mit dem Kreismittelpunkt zusammenfällt. Wir können diesen Schwerpunkt mit den Hebelgesetzen von Archimedes bestimmen. Zunächst fassen wir je zwei und zwei Punkte mit einer Sehne zusammen (Abb. 2). Deren Mittelpunkt ist der lokale Schwerpunkt des jeweiligen Punktepaares. Nun schließen wir den fünften Punkt zu einer Sehne an. Dazu verbinden wir diesen Punkt mit dem Mittelpunkt der Sehne und dritteln. Der Drittelpunkt näher beim Mittelpunkt der Sehne ist nun lokaler Schwerpunkt der beteiligten drei Punkte. Das ist natürlich nichts anderes als die Schwerpunktskonstruktion im Dreieck. Schließlich verbinden wir diesen Dreiecksschwerpunkt (an welchem drei Punktmassen angreifen) mit dem Mittelpunkt der anderen Sehne (an dem zwei Punktmassen angreifen). Diese Strecke teilen wir im Verhältnis , wobei der Teilpunkt näher beim drei-Massen-Schwerpunkt zu wählen ist. So erhalten wir den Schwerpunkt aller fünf Massen. In unserem Beispiel fällt dieser Schwerpunkt mit dem Kreismittelpunkt zusammen. Die Figur ist also in sich ruhend.

Eine solche Figur nennen wir eine Gleichgewichtsfigur. Sie besteht aus n Punktmassen auf einem Kreis so, dass deren Schwerpunkt mit dem Kreismittelpunkt zusammen fällt.

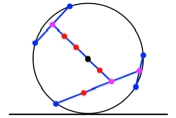
Abb. 2: Schwerpunkt im Mittelpunkt.

Im folgenden arbeiten wir mit dem Einheitskreis und später mit der Einheitskugel.

2 Diametrale Punkte

Das einfachste Beispiel einer Gleichgewichtsfigur besteht aus zwei diametralen Punkten und . Wir haben also einen Thaleskreis.

Nun wählen wir zusätzlich einen beliebigen Punkt C auf dem Kreis (Abb. 3).

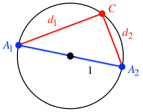
Abb. 3: Kreis des Thales

Das Dreieck ist rechtwinklig mit dem rechten Winkel in C, und nach dem Satz des Pythagoras ist die Summe der Quadrate der Abstände von C zu den Punkten und konstant, nämlich 4.

Bei zwei Paaren diametraler Punkte , beziehungsweise , erhalten wir ein Rechteck (Abb. 4) und durch zweimalige Anwendung des Satzes von Pythagoras die Summe der Quadrate der Abstände von einem beliebigen Punkt C auf dem Umkreis den Wert 8.

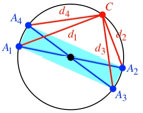
Abb. 4: Rechteck

Entsprechend ergibt sich für ein beliebiges punktsymmetrisches Sehnen-2n-Eck bei n-facher Anwendung des Satzes von Pythagoras die invariante Summe . Das ist eine Verallgemeinerung des in [Stoeter / Wohlrabe 2011] vorgestellten Sachverhaltes.

3 Regelmäßige Vielecke

Was erhalten wir nun für einen Punkt C auf dem Umkreis eines gleichseitigen Dreieckes (Abb. 5)? Wir haben jetzt sozusagen ein gleichseitiges Dreieck als „Hypotenuse“ und drei von C aus laufende „Katheten“. Dabei stehen zwei Fragen im Raum: Ist die Summe der Quadrate der Abstände von C eine Invariante, und wenn ja, wie groß ist diese.

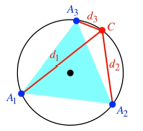
Abb. 5: Gleichseitiges Dreieck

Die zweite Frage können wir anhand von symmetrischen Sonderfällen angehen.

Im Sonderfall der Abbildung 6 ist und , also .

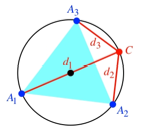
Abb. 6: Symmetrischer Sonderfall

Wenn wir den Punkt C in die Ecke legen (Abb. 7), erhalten wir und , also wiederum .

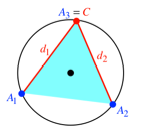
Abb. 7: Sonderfall

Bei einem regelmäßigen n-Eck ergibt sich entsprechend die Summe . Dies ist eine Verallgemeinerung des Ergebnisses von [Stoeter / Wohlrabe 2009].

4 Im Raum

Wir können sogar in den Raum gehen. Wir legen das gleichseitige Dreieck in die Äquatorebene der Einheitskugel und den Punkt C in den Nordpol. Dann ist und wiederum .

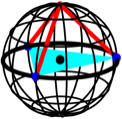
Abb. 8: In der Einheitskugel

Wenn wir allerdings den Punkt C in allgemeiner Lage auf der Kugel wählen, gibt es keinen trivialen Zugang zur Summe der Quadrate der Abstände (Abb. 9).

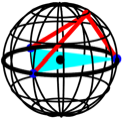
Abb. 9: Und?

5 Allgemeiner Fall

Wir gehen aus von einer Gleichgewichtsfigur mit n Punkten. Wir haben also n gleiche Massenpunkte auf dem Einheitskreis oder der Einheitssphäre, so dass deren Schwerpunkt der Kreis- bzw. Kugelmittelpunkt M ist.

Wir führen eine Koordinatensystem mit dem Ursprung in M ein. Es sei:

Da der Kreis- bzw. Kugelradius 1 ist, haben wir , und wegen der Gleichgewichtseigenschaft ist der Ursprung der Schwerpunkt, also .

Nun sei C mit dem Ortsvektor ein beliebiger Punkt. Damit ist und:

Wegen und folgt:

Damit ist:

Die Summe der Quadrate der Abstände ist also genau dann , wenn sich der Punkt C auf dem Einheitskreis oder der Einheitssphäre befindet.

6 Kreisbögen

Wir ersetzen die Abstände durch Kreisbögen auf dem Einheitskreis oder der Einheitskugel.

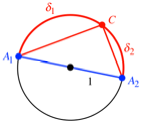
Abb. 10: Kreisbögen

Im einfachsten Fall der Abbildung 10 ist und damit:

Wir werden sehen, dass die Summe der Kosinuswerte der Bögen allgemeine Null ist.

Zunächst einige Beispiele:

Wir legen ein regelmäßiges Sechseck in die Äquatorebene und wählen den Punkt C beliebig auf der nördlichen Hemisphäre (Abb. 11). Wir erhalten sechs Kreisbögen. Da sich je zwei Kreisbögen zu einem Halbkreis ergänzen, haben wir drei mal die Situation der Abbildung 10. Damit ist .

Abb. 11: Die rote Spinne

Wenn wir allerdings mit einem regelmäßigen Fünfeck beginnen (Abb. 12), haben wir keinen trivialen Zugang zu den Kosinuswerten der fünf Kreisbögen.

Abb. 12: Summe der Kosinuswerte?

Die Gleichgewichtsfigur selber kann auch räumlich sein, zum Beispiel ein reguläres Tetraeder (Abb. 13). Auch hier ist die Summe der Kosinuswerte der vier Bögen nicht direkt ablesbar.

Abb. 13: Räumliche Gleichgewichtsfigur

Wir können aber leicht beweisen, dass allgemein gilt:

Zunächst ist . Daraus ergibt sich:

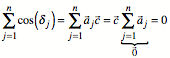
7 Gleichgewichtsfiguren

In der Ebene sind alle regelmäßigen Vielecke, das Zweieck eingeschlossen, Beispiele von Gleichgewichtsfiguren. Wir können aber auch zwei verschiedene Gleichgewichtsfiguren mit demselben Umkreisradius überlagern und erhalten so eine neue, nicht mehr regelmäßige Gleichgewichtsfigur. Die Abbildung 14 zeigt zwei verschiedene Gleichgewichtsfiguren mit je 5 Punkten, das regelmäßige Fünfeck (Abb. 14a) und eine Überlagerung eines gleichseitigen Dreieckes mit einem Zweieck (Abb. 14b).

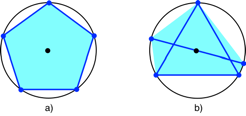
Abb. 14: Gleichgewichtsfiguren

Gleichgewichtsfiguren im Raum sind etwa die platonischen Körper, die archimedischen Körper sowie Doppelpyramiden mit einem regelmäßigen Vieleck in der Äquatorebene als Basis und je einer Spitze in den Polen. Wie in der Ebene können wir zwei Gleichgewichtsfiguren überlagern oder einen Konstruktionsalgorithmus anwenden.

8 Konstruktionsalgorithmus für Gleichgewichtsfiguren

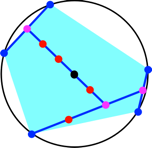
Die Abbildung 15 zeigt eine recht unregelmäßige Gleichgewichtsfigur mit fünf Punkten.

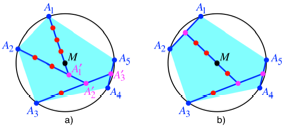
Abb. 15: Hebelmechanismen

Die Figur der Abbildung 15a wird wie folgt konstruiert: Wir beginnen mit einem beliebigen Punkt auf dem Kreis und zeichnen dann den Punkt so, dass der Kreismittelpunkt M die Strecke im Verhältnis 4:1 teilt. Das Teilverhältnis ist durch die gelben Hilfspunkte angedeutet. Hier kommen die Hebelgesetze ins Spiel, denn an wird die Gesamtmasse der vier restlichen Punkte angreifen. Nun wählen wir auf dem Kreis und konstruieren derart, dass der Punkt die Strecke im Verhältnis 3:1 teilt. Dann wählen wir auf dem Kreis und bestimmen so, dass die Strecke im Verhältnis 2:1 teilt.

Schließlich zeichnen wir und so, dass Mittelpunkt der Strecke wird. Dies geschieht zum Beispiel mit einer Spiegelung des Kreises an .

Dieser allgemeine Konstruktionsalgorithmus lässt sich entsprechend der Eckenzahl n verallgemeinern und auch auf den Raum übertragen.

Die Abbildung 15b (entspricht der Abbildung 2) zeigt dieselben fünf Punkte mit einer anderen Hebeltopologie. Wie viele Hebeltopologien gibt es zu einer Gleichgewichtsfigur mit n Punkten?

9 Abzählung der Hebeltopologien

Wir bezeichnen mit die Anzahl der Hebeltopologien beim n Punkten.

9.1 Beispiele

Die Tabelle 1 gibt einige Beispiele, welche allenfalls von Hand ausgezählt werden können. Das erste Beispiel, also , ist allerdings nicht sinnvoll, da es keine Gleichgewichtsfigur mit nur einem Punkt geben kann. Allerdings passt diese Festlegung zu den nachfolgenden Formeln. Sie ist also zu verstehen wie etwa die „unsinnige“ Definition .

Tab. 1: Beispiele

9.2 Rekursion

Wir gehen nun davon aus, dass wir für kennen und suchen eine Rekursionsformel für .

Dazu unterteilen wir die n in zwei nichtleere disjunkte Teilmengen von k und Punkten. Dies geht auf Arten. Zur Teilmenge von k Punkten können wir auf Arten den Schwerpunkt konstruieren, zur Komplementärmenge auf Arten. Nun unterteilen wir die Verbindungsstrecke der Schwerpunkte der beiden Teilmengen im Verhältnis und erhalten so den Schwerpunkt der n Punkte. Somit ist:

Der Faktor ist erforderlich, weil die Teilmengen für j Punkte sowohl für wie auch für berücksichtigt werden. Die Summe läuft von 1 bis , weil die Teilmengen mindestens 1 und höchstens Elemente enthalten.

Mit Hilfe dieser Rekursionsformel und dem Startwert erhalten wir die Werte der Tabelle 2, Spalte 2.

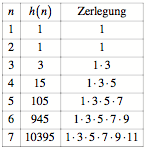
Tab. 2: Beispiele. Zerlegung

Die Zahlen werden rasch groß. Aus der dritten Spalte der Tabelle 2 ergibt sich die Vermutung für eine explizite Formel:

Für den Beweis der expliziten Formel arbeiten wir mit den Catalan-Zahlen. Die Anregung dazu erhielt ich von P. W. in A..

9.3 Catalan-Zahlen

Eugène Charles Catalan, (1814 in Brügge – 1894), belgischer Mathematiker

Definition der Catalan-Zahlen:

Numerisch:

Für die Catalan-Zahlen gilt die Rekursion von Segner 1758 (Johann Andreas von Segner, 1704 in Pressburg (Bratislava) – 1777 in Halle):

Mit Hilfe der Catalan-Zahlen können wir die vermutete explizite Formel umschreiben:

9.4 Beweis der expliziten Formel

Zu zeigen ist: erfüllt die Rekursion

mit dem Startwert .

Startwert: ok.

Rekursion:

Linke Seite:

Rechte Seite:

Nun verwenden wir die Rekursion von Segner:

Zunächst ist:

Durch Umindizieren ergibt sich:

Somit erhalten wir für die rechte Seite:

Dies ist gleich der linken Seite. — Die explizite Formel ist damit bewiesen.

10 Regelmäßige Vielecke

Die Abbildung 16 zeigt den Konstruktionsalgorithmus für regelmäßige Vielecke.

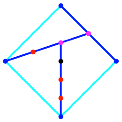
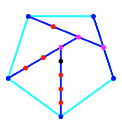
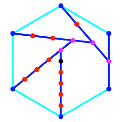
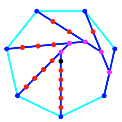
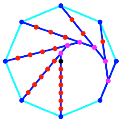
Abb. 16: Konstruktionsalgorithmus in regelmäßigen Vielecken

Es zeichnet sich eine Grenzfigur ab. Die Abbildung 17 zeigt die Situation für und .

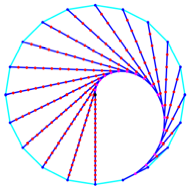
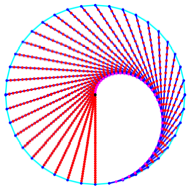
Abb. 17: Eine Grenzfigur zeichnet sich ab

Die Grenzfigur ist ein halbes Herz. Es kann zu einem ganzen Herz erweitert werden (Abb. 18).

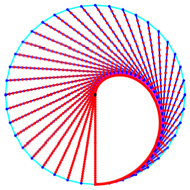
Abb. 18: Herz

Die Herzkurve hat die Parameterdarstellung:

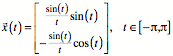
Es handelt sich also nicht um die übliche Kardioide. Die Abbildung 19 zeigt unsere Herzkurve (rot) und die Kardioide (blau).

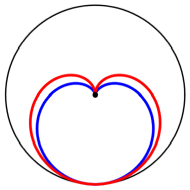
Abb. 19: Herzkurve und Kardioide

Die Kardioide hat nämlich die Parameterdarstellung:

Literatur

[Stoeter / Wohlrabe 2009] Stoeter, Carsten und Wohlrabe, Klaus: Vergessene Längen. Besondere Eigenschaften regulärer Vielecke. MNU Der mathematische und naturwissenschaftliche Unterricht 62/1 (15. 1. 2009), S. 10-14, ISSN 0025-5866, © Verlag Klaus Seeberger, Neuss.

[Stoeter / Wohlrabe 2011] Stoeter, Carsten und Wohlrabe, Klaus: Zu: Vergessene Längen. MNU Der mathematische und naturwissenschaftliche Unterricht 64/1 (15. 1. 2011), S. 56, ISSN 0025-5866, © Verlag Klaus Seeberger, Neuss.

[Walser 2011] Walser, Hans: Gleichgewichtsfiguren: Thales, Pythagoras und Archimedes. MNU Der mathematische und naturwissenschaftliche Unterricht 64/7 (15. 10. 2011), S. 442-443, ISSN 0025-5866.

Hans Walser

Mathematisches Institut

Universität Basel

Rheinsprung 21

CH 4051 Basel

Tel. +4161 267 26 87

hwalser at bluewin dot ch